俯仰角对鸭式布局飞机摇滚运动的影响与机理分析

魏德宸, 史志伟, 昂海松, 付军泉, 朱佳晨

(南京航空航天大学 航空宇航学院, 江苏 南京 210016)



俯仰角对鸭式布局飞机摇滚运动的影响与机理分析

魏德宸, 史志伟*, 昂海松, 付军泉, 朱佳晨

(南京航空航天大学 航空宇航学院, 江苏 南京 210016)

为了研究鸭式布局飞机的摇滚运动，设计了一种包括鸭翼、脊型前体、边条翼、主翼和垂尾的模型，进行滚转自由度释放、静态测力、动导数试验和烟线流场显示多种技术手段相结合的风洞试验。首先为了得到摇滚从发生到消失的全过程，进行了俯仰角范围为12° ～52°、间隔1°测量的滚转自由度释放试验；结果表明对应于不同的俯仰角，鸭翼布局飞机的摇滚运动也具有不同的性质，其平衡点和运动形式均发生变化。接着静态测力和动导数试验证实：在翼体结构的多涡系影响下，摇滚可在零度平衡点和非零平衡点位置处发生；且运动可为极限环和非极限环形式。最后通过流场显示，分析了在不同迎角时鸭式布局飞机形成翼体摇滚的可能的流动机理。

鸭翼；翼体摇滚；非零平衡点；非极限环；流场显示

0 引 言

随着人们对非线性涡升力认识的不断深化和先进控制技术的应用，现代飞行器的可控迎角不断增大。然而大迎角飞行时,常常会诱发非指令的自激运动，摇滚正是其中一种严重的动态表现形式。这种以绕体轴滚转振荡为主的自激运动不仅缩小了飞行包线，限制了战斗机的机动性和敏捷性, 而且严重影响了安定性和操纵性, 甚至引起结构强度问题导致飞机解体。

Ericsson根据飞行器产生摇滚的机理对摇滚现象分为三类[1-4]: (1) 细长体摇滚; (2) 常规机翼摇滚; (3) 翼身组合体摇滚。翼身组合体摇滚是最接近真实飞行器摇滚的类型，然而由于问题的复杂性等原因，翼体摇滚相应研究开展的较少。隶属于北约组织(NATO)的航空研究与发展顾问小组(AGARD)发起的一项针对解决飞行器高机动飞行的项目中，翼体摇滚的研究和预测作为其中重要组成部分，开展了针对编号为“WG16A”翼身组合体模型的风洞试验研究[5]。Guglieri则通过前体形状分别为圆柱和圆锥不同构型的80° 后掠三角翼的风洞试验，研究前体涡的改变对摇滚特性的影响[6]。作为NASA和美国海军联合牵头的翼突然失速(AWS)计划的一部分[7-9]，自由摇滚(FTR)和测力试验被应用在多种真实飞行器缩比模型的风洞试验中。其中Owens等研究了前后缘襟翼角度变化、涡流发生器等对F-35战斗机摇滚的影响[10]。Green等研究了F/A-18战斗机的机翼厚度、弯度等参数对摇滚运动的影响[11-12]。类似的AV-8B和F-16C的缩比模型也通过风洞试验来用于验证和预测实际飞行中可能出现的摇滚现象[13]。近年国内多家单位也开展了翼体摇滚的研究工作, 张涵信等针对翼体摇滚运动中的静稳定性和动稳定性进行了大量研究和分析，提出了静态和动态稳定性分析判据[14-16]。马宝峰、荣臻等重点分析了前体涡在细长前体结构的翼身组合体摇滚中的诱导作用[17-18]。 张杰等针对一种先进作战飞机进行了跨声速的自由滚转试验，并对横滚运动进行了量化的评估[19]。孙海生和姜裕标研究了一种战斗机模型的摇滚风洞试验，结果表明单独前体和翼身组合体结构均可产生摇滚；且翼身组合体在不同迎角范围，具有不同的摇滚特征[20]。王兵等开展了尖拱旋成体和小后掠梯形机翼组合体在人工转捩条件下的摇滚研究，扩展了低速风洞中进行摇滚试验的雷诺数范围[21]。但目前国内发表的翼体摇滚文献多基于细长旋成体和机翼的简单结构模型，国外公开文献也缺乏针对复杂结构飞行器特别是鸭式布局飞机所引发的翼体摇滚的流场研究和机理分析。

1 试验设备及模型

1.1 试验风洞

试验是在南京航空航天大学开口回流式风洞中

进行的，风洞实验段长×宽×高：1.7 m×1.5 m×1.0 m，最大风速35 m/s，最小稳定风速3 m/s。风洞流场品质良好，俯仰方向气流偏角|α|≤0.5°，偏航方向气流偏角|β|≤0.5°，湍流度ε≤0.07%。

1.2 试验模型

试验所采用的为鸭式布局飞机模型，全长0.66 m，主翼展长0.5 m。前体为脊型截面；鸭翼具有-20° 的固定偏角(前缘向下)，在主翼迎角较大时，鸭翼的实际迎角较小；鸭翼与主翼前缘后掠角均为Λ=50°。具体参数如图1所示。

图1 试验模型Fig.1 Test model

1.3 试验设备

试验系统台为图2所示的五自由度并联机构，可实现模型俯仰、偏航和滚转三个方向的运动，以及这三个方向上的组合运动[22]。本次试验在此机构上进行了静态测力与动导数测量，所用数据采集卡的分辨率为16位, 最大采样速率250 kS/s。将天平支杆更换为自由摇滚装置可进行自由摇滚试验[23]。自由摇滚装置如图3所示，滚转角测量精度为0.1°。

图2 五自由度并联机构Fig.2 The 5 DOF dynamic test mechanism

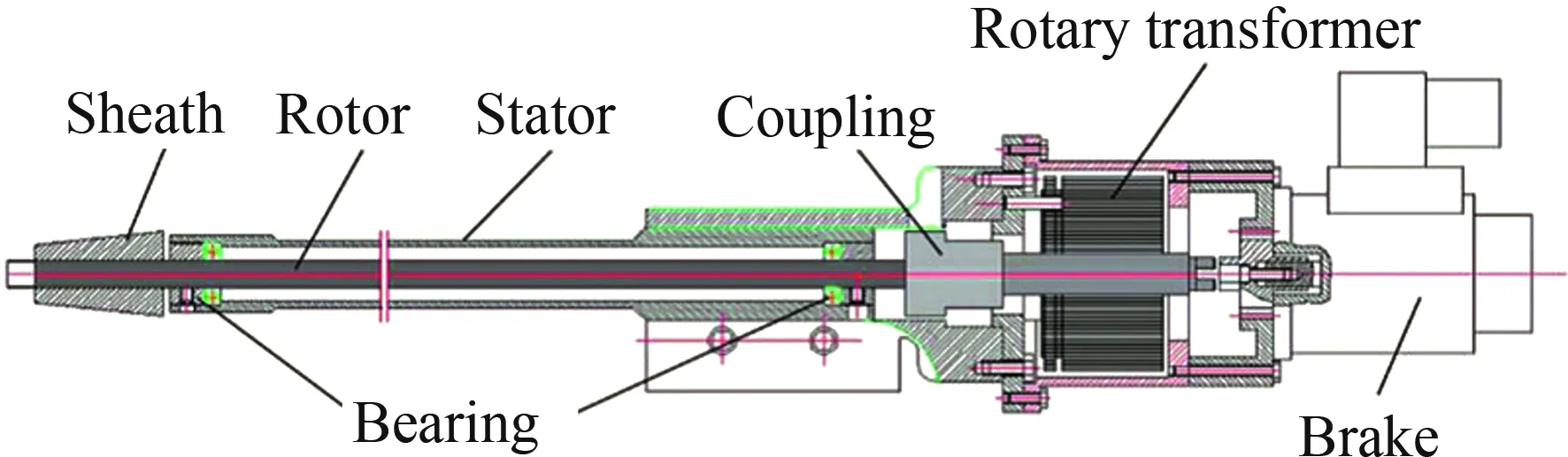
图3 自由摇滚装置[23]Fig.3 Free-to-roll test sting[23]

2 滚转自由度释放与稳定性分析

2.1 翼身组合体自由度释放

摇滚本质上是多自由度耦合的运动，但其运动形式为以绕体轴滚转振荡为主的自维持动态运动，滚转是最主要的自由度，有文献[24-25]指出，一定情况下，可采用单滚转自由度假设来研究飞行器的动态摇滚特性。为分析鸭式布局飞机翼体摇滚的特性，进行了θ=12°～52° 大俯仰角范围的自由摇滚试验，包括了摇滚从发生到消失的全过程。图4给出了鸭式布局飞机不同俯仰角θ范围内典型的滚转角φ时间历程，试验风速为V=25 m/s。

从摇滚运动的形式分析：如图4(a)所示，θ=12° 时滚转运动呈现微小抖动。原因可能为小迎角下翼体表面以附着流动为主，摇滚尚未发生，非均匀来流中小扰动的作用使得滚转角发生变化[26]。图4(b～d)所示，θ=23°、31° 和35° 时摇滚运动频率和振幅存在明显波动，伴有间歇、猝发等特征。可能的原因为前体涡、鸭翼前缘涡、边条涡和主翼前缘涡的强弱变化和相互干扰[13]，使得摇滚运动不是规则的等幅振荡(不同于常见的细长三角翼摇滚)，而是非极限环运动，其机理将在后续的流场测量中进行分析。在图4(e)中，θ=45° 时摇滚呈现中小迎角范围内未出现的准极限环运动形式，这时的摇滚运动可能类似于细长体摇滚。此时对摇滚起主要作用的可能是脊型前体产生的前体涡，其他涡系基本完全破裂。这时的主机翼也许只是提供滚转力矩所需力的作用面；或去除主机翼，机身相当于细长体模型，摇滚特征参数会发生变化，但极限环形式的摇滚现象仍可能发生[20,27]。而如图4(f)所示，θ=52° 时滚转运动再次呈现无规则地微小抖动，摇滚运动消失。此时的运动状态和θ=12° 相似，但机理完全不同，可能的原因为此迎角下包括前体涡在内的多个涡系已完全破裂，翼体表面被湍流覆盖，不能产生较大的气动力矩。摇滚运动形式随俯仰角变化的机理分析具体见第3节。

(a) θ=12°

(c) θ=31°

(e) θ=45°

(b) θ=23°

(d) θ=35°

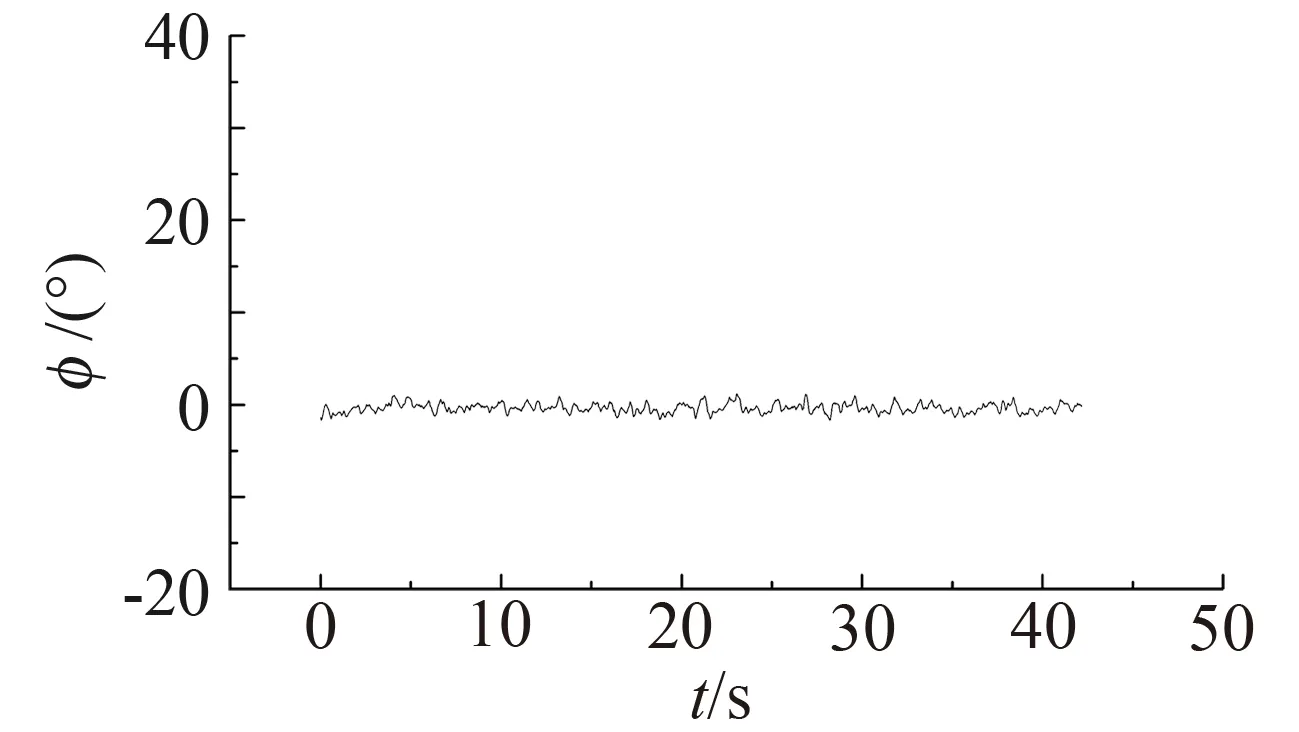
(f) θ=52°

图4 鸭式布局飞机不同俯仰角下的典型摇滚时间历程
Fig.4 Typical Roll angle time history for the canard-configuration aircraft model at different pitch angles

从平衡点位置分析，此鸭式布局飞机随俯仰角变化，翼体摇滚从发生到消失的过程中滚转中心角也随之改变的。除了常规的φmean≈0°，在滚转一侧也具有多个非零平衡点。如图4所示θ=12° 时，初始时平衡点为静态平衡点，中心角φmean≈0°；θ=23° 时，模型处于翼体摇滚状态(证明见2.3节)，此时的摇滚平衡点为φmean≈-12°；随着俯仰角的增加，如图4(c)所示θ=31° 时,模型仍处于翼体摇滚状态，但此时的平衡点回到φmean≈0°；θ=35° 时, 鸭式布局飞机围绕更大的滚转中心角φmean≈26° 做摇滚运动；俯仰角度增加，如图4(e)所示θ=45° 时，摇滚平衡点再次回到φmean≈0°；俯仰角继续增加，如图4(f)所示θ=52° 时，摇滚现象逐渐消失，0° 摇滚平衡点变为0° 静态平衡点。

2.2 滚转中心角随俯仰角变化规律分析

为了更好的分析摇滚发展规律，对自由摇滚试验得到的滚转角度序列进行数值分析。处理公式如下所示[28]，其中φmean为滚转中心角;φi为时间历程下的滚转角。

如图4(b)、(d)所示摇滚运动可在滚转对称两侧发生，为便于分析摇滚发展规律，将中心角取绝对值得到平衡点位置的绝对值随俯仰角变化曲线，如图5所示。

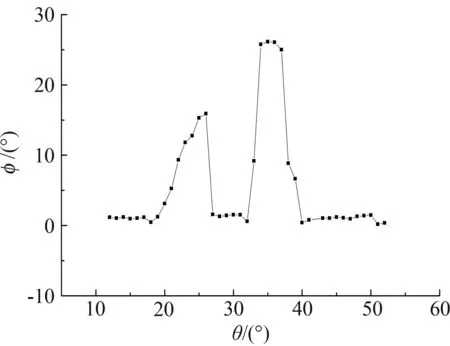
图5 鸭式布局飞机滚转中心角随俯仰角变化曲线Fig.5 Mean roll angles change with increasing pitch angle for canard-configuration aircraft

如图5所示，θ=12°～18° 时，初始时φmean≈0°为静态平衡点；在θ=19°～26° 范围，随着俯仰角的增加，摇滚在这一阶段产生，平衡点位置由φmean≈0° 逐渐变动到φmean≈16°；θ=27°～32° 时，摇滚平衡点再次回到φmean≈0°；θ=33°～39° 时，摇滚平衡点又一次位于非零位置；θ=40°～50° 范围内摇滚平衡点再次回到零度位置；θ≥51° 时，摇滚消失，模型在滚转角零度位置附近稳定。通过θ变化范围40°、间隔Δ=1° 的滚转自由度释放试验，可知在不同的俯仰角范围，翼体摇滚的影响涡系可能也不同，具体分析见第3节。

2.3 翼体摇滚的稳定性分析

翼体摇滚为单自由度滚转运动时，其滚转运动公式可写为：

试验风速仍为25m/s，通过两侧滚转位置的静态测力和动导数试验，获得了图4中非极限环和极限环两种摇滚运动形式典型俯仰角时的滚转力矩系数Cl和滚转阻尼导数Clp，见图6和图7。

图6 不同俯仰角的滚转力矩系数ClFig.6 Static roll moment coefficients at different pitch angles

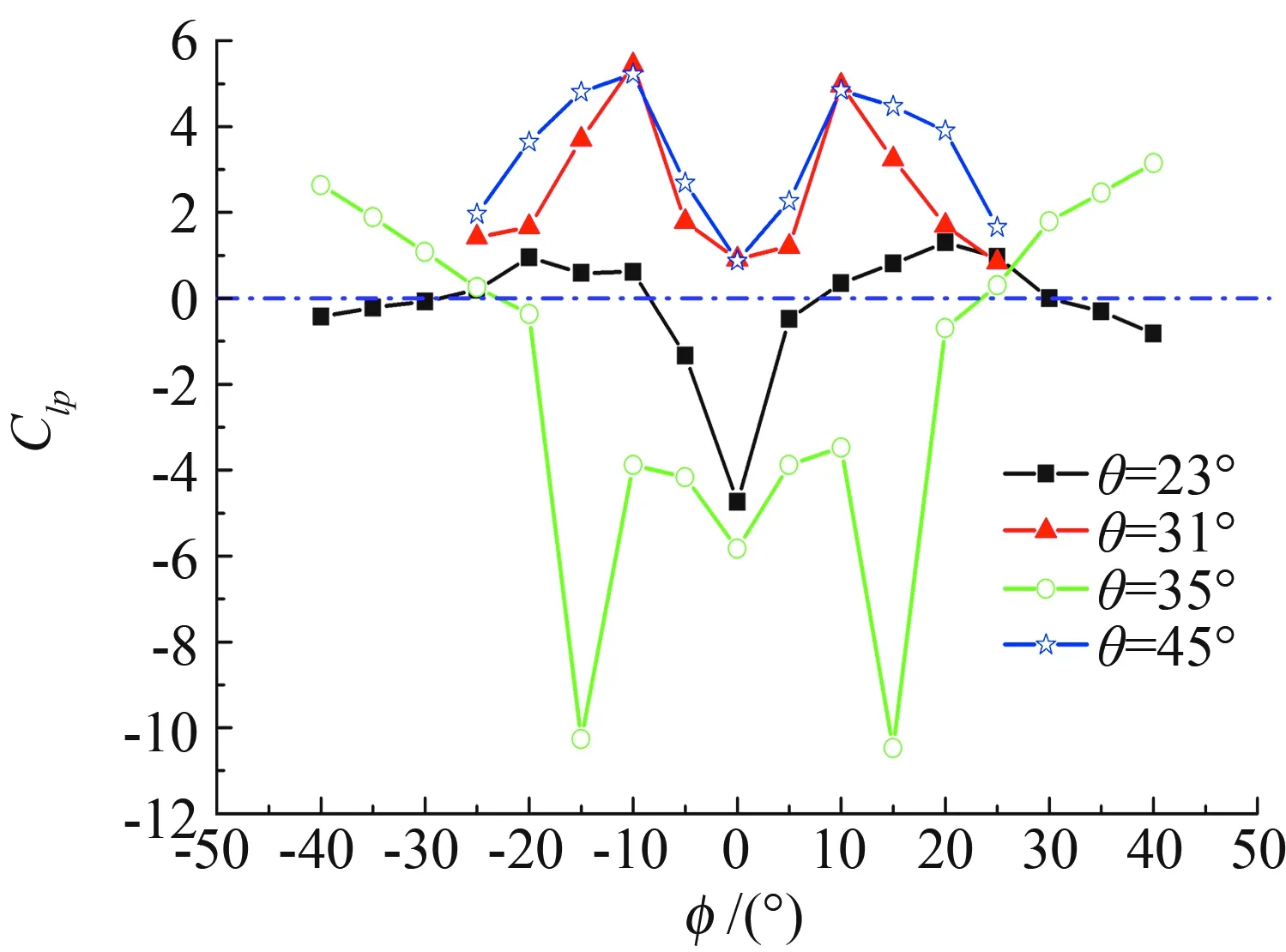
图7 不同俯仰角的滚转阻尼导数ClpFig.7 Dynamic damping derivatives at different pitch angles

首先对不同俯仰角时，φ=0° 的滚转力矩系数相对滚转角的斜率进行总结。滚转角φ=0°附近滚转力矩系数Cl均过零点，力矩是平衡的。如图6所示，θ=23° 时斜率为正，说明模型在φ=0° 是静态不稳定的，摇滚不能在此中心角度发生；θ=31° 时斜率为负，说明模型在φ=0° 静态稳定，该滚转角为翼体摇滚的一个静态平衡点或者摇滚的平衡点；同理θ=35° 时零度滚转角的Clp斜率再次变为正；θ=45° 时其斜率又为负值。Clp曲线斜率在φ=0° 时的正负变化和图4的零度平衡点和非零平衡点的变化是一致的，理论分析结果和试验结果重合。再观测图6中滚转力矩系数为零时对应的非零滚转角，θ=23° 且φ≈±12°时斜率为负，θ=35° 且φ≈±26° 时斜率也为负。最后结合图7动导数结果，当静态力矩斜率为负且动导数为正值，对应滚转角才为摇滚平衡点，可知φ≈±12°、0°、±26°、0° 依次为θ=23°、31°、35°、45° 时的摇滚平衡点。

3 流场显示与机理分析

鸭式布局飞机表面的涡系分布如图8所示。其中脊形前体涡与鸭翼前缘涡同向旋转且位置较近，在鸭翼翼面上绕合在一起，形成前体与鸭翼前缘卷绕涡；边条涡和主翼前缘涡绕合在一起，形成了边条与主翼前缘卷绕涡。前体与鸭翼前缘卷绕涡位于内侧，且沿流向发展距离较长，故在主翼面的位置较高；边条与主翼前缘卷绕涡受到同向旋转的前体与鸭翼前缘卷绕涡的外推作用，位于主翼外侧，且沿流向发展距离短，涡心位置也较低[31]。

图8 鸭式布局飞机的涡系分布Fig.8 Vortex structures over canard-configuration aircraft

为了研究不同俯仰角时，鸭式布局飞机翼体摇滚具有不同性质的原因，应用烟线和激光片光技术在如图1截面S所示的主翼1/2弦线位置,φ=0° 时进行流场观测。

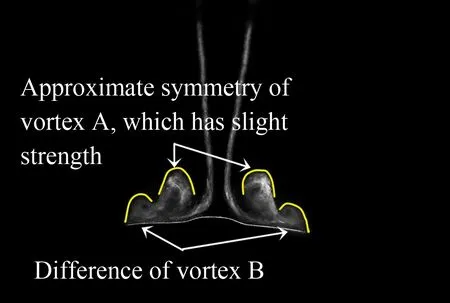
如图9(a)所示，距离鸭式布局飞机中轴线距离较近的涡为脊型前体和鸭翼前缘形成的前体与鸭翼前缘卷绕涡，在图示中将其命名为“Vortex A”; 距离轴线更远的涡则为边条和主翼前缘形成的边条与主翼前缘卷绕涡，在图示中将其命名为“Vortex B”。

在θ=12° 时，前缘后掠角为50° 的下偏鸭翼和主翼产生的前缘涡强度较弱；而脊型前体和边条均可产生稳定的涡流；故此时翼身组合体两侧的涡流分布较为对称，飞行器处于静态平衡状态。θ=23° 时，脊型前体涡仍然稳定[32-33]，而此时鸭翼的实际迎角为23°-20°=3°，所产生的前缘涡强度弱，故前体与鸭翼前缘卷绕涡如图9(b)所示仍较为对称；主翼前缘涡变得不对称，使得两侧的边条与主翼前缘卷绕涡的对称性遭到破坏，如图9(b)所示机身左侧远离中轴线的涡位置较右侧高，φ≈0° 时模型不再静态稳定。鸭式布局模型在如图4(b)所示的φ≈-12° 中心角产生翼体摇滚的主要因素，可能为较弱的前体与鸭翼前缘卷绕涡和不对称性的边条与主翼前缘卷绕涡的共同影响。

(a) θ=12°

(b) θ=23°

(c) θ=31°

(d) θ=35°

(e) θ=45°

(f) θ=52°

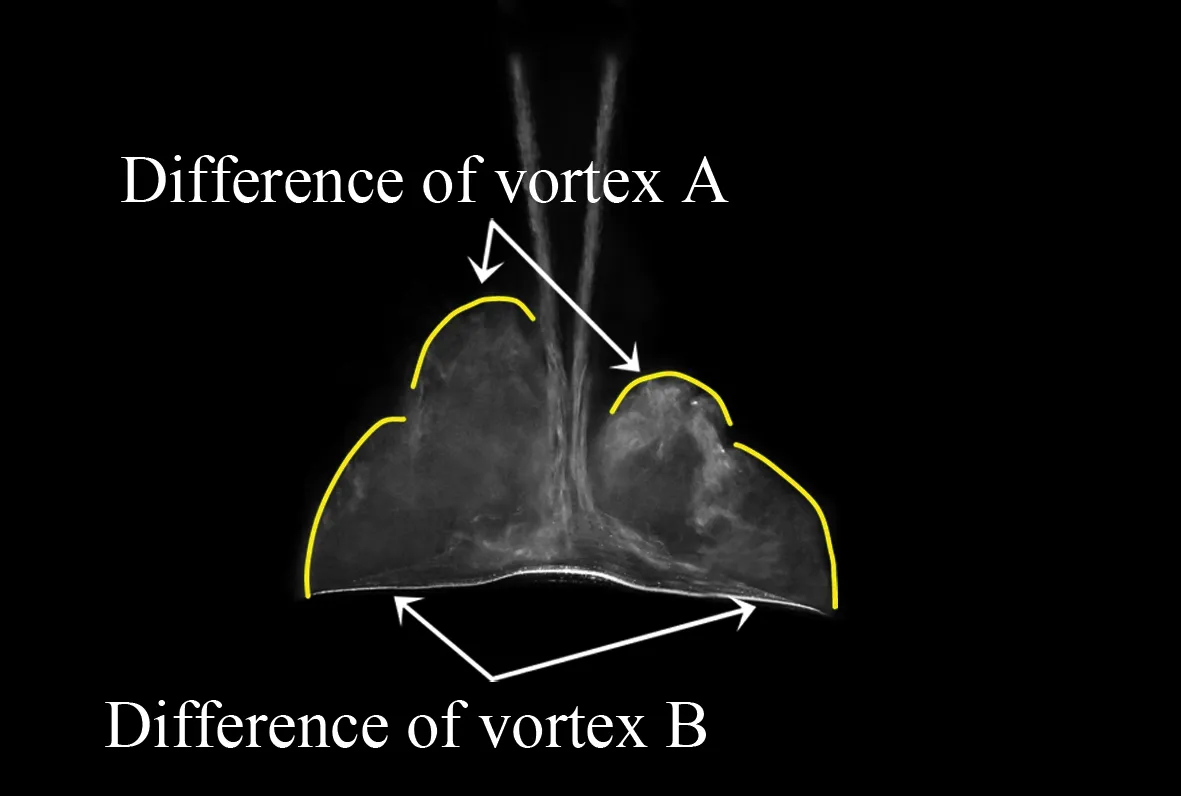
θ=31° 时，如图9(c)所示前体涡进一步增强使得前体与鸭翼前缘卷绕涡也较为稳定；而此时由于主翼前缘涡的进一步失衡使得边条与主翼前缘卷绕涡的不对称性增加。在此迎角下摇滚发生在如图4(c)所示φ≈0° 的原因，可能为更强且较为对称的前体与鸭翼前缘卷绕涡的约束[33]和不对称的边条与主翼前缘卷绕涡的扰动。

θ=35° 时，由于此时鸭翼前缘涡的不对称性增加使得前体与鸭翼前缘卷绕涡也较为不对称；同时两侧的边条与主翼前缘卷绕涡如图9(d)所示差异也较大。此时摇滚发生在如图4(d)所示φ≈26° 的原因，可能为均失去对称性的前体与鸭翼前缘卷绕涡和边条与主翼前缘卷绕涡共同所致。类似的，在Gresham等的研究工作中，发现与鸭翼和主翼后掠角度相同的50° 后掠三角翼具有较大的非零平衡点[34]；且比较可知，对于本次试验中采用的鸭式布局模型， 摇滚可在俯仰角更大时发生，可能的原因为脊型前体[32-33]，以及边条翼带来的稳定性作用[35-36]。

θ=45° 时，此时的摇滚和细长体摇滚类似，如图4(e)所示，不同之前俯仰角范围下的非极限环，运动已表现为准极限环形式，且摇滚中心角为φ≈0°；可能的原因为如图9(e)所示，此时对翼体摇滚起主要作用的是脊型前体产生的前体涡，其他的涡系均已完全破裂，而机身相当于细长体模型，主机翼也许只是提供滚转力距的作用面，类似的情况在Ross等在只保留机身的摇滚试验中也有发生[37]。θ=52° 时，随着俯仰角的继续增大，如图9(f)所示脊型前体涡也已完全破裂，全机涡的破裂使得摇滚现象消失，θ=45° 时的零度摇滚平衡点变为如图4(f)所示的零度静态平衡点。

4 结 论

1) 随俯仰角变化，由于多涡系的影响，鸭式布局飞机摇滚具有不同的平衡点和运动形式，可为非零小角度平衡点的非极限环运动、零度平衡点非极限环运动、非零大角度平衡点的非极限环运动和零度平衡点准极限环运动。

2) 稳定性分析表明，对于存在多涡结构的鸭式布局飞机，通过地面的测力和动导数试验可以判断和预测其摇滚运动。

3)θ=19°～26°范围，鸭式布局飞机的不对称性的边条与主翼前缘卷绕涡可能是促发摇滚的主要涡系，前体与鸭翼前缘卷绕涡具有一定稳定作用，但涡强较弱，共同的作用使得摇滚在较小中心滚转角发生；θ=27°～32° 时，前体涡强度的增加使得摇滚中心回到零度位置；θ=33°～39° 时，前体与鸭翼前缘卷绕涡不对称性的增加使得摇滚平衡点位于较大的非零位置；θ=40°～50° 范围内其他涡均已破裂，不对称的前体涡可能是引起摇滚的主要原因。

4)随着俯仰角的改变，一方面前体或主翼等结构所产生涡的相对强弱变化，形成了不同的摇滚促发流场；另一方面前缘涡、前体涡、边条涡等涡系对于翼体摇滚或诱导或稳定的不同作用，共同施加于翼身组合体。这两方面因素的影响使得鸭式布局飞机在不同俯仰角具有不同性质的摇滚运动。

[1]Ericsson L E. Slender wing rock revisited[J]. Journal of Aircraft, 1993, 30(3): 352-356.

[2]Ericsson L E. Wing rock analysis of slender delta wings, Review and extension[J]. Journal of Aircraft, 1995, 32(6): 1221-1226.

[3]Ericsson L E. Wing rock generated by forebody vortices[J]. Journal of Aircraft, 1989, 26(2): 110-116.

[4]Ericsson L E. Various sources of wing rock[J]. Journal of Aircraft, 1990, 27(6): 488-494.

[5]North Atlantic Treaty Organization. Cooperative programme on dynamic wind tunnel experiments for manoevring aircraft. AGARD AR-305[R]. Brussels: AGARD, 1996.

[6]Guglieri G. A comprehensive analysis of wing rock dynamics for slender delta wing configurations[J]. Nonlinear Dyn, 2012, 69: 1559-1575.

[7]Hall R M, Woodson S H. Introduction to the abrupt wing stall program[J]. Journal of Aircraft, 2004, 41(3): 425-435.

[8]Hall R M, Woodson S H, Chambers J R. Overview of the abrupt wing stall program[J]. Progress in Aerospace Sciences, 2004, 40(7): 417-452.

[9]Hall R M. Introduction: Abrupt wing stall program, part 2[J]. Journal of Aircraft, 2005, 42(3): 577-577.

[10]Owens D B, McConnell J K, Brandon J M, et al. Transonic free-to-roll analysis of the F-35 (joint strike fighter) aircraft[J]. Journal of Aircraft, 2006, 43(3): 608-615.

[11]Green B E, Ott J D. FA-18C to E wing morphing study for the abrupt-wing-stall program. AIAA 2003-0925[R]. Reston: AIAA, 2003.

[12]Green B E, Ott J D. FA-18C to E wing morphing study for the abrupt-wing-stall program[J]. Journal of Aircraft, 2005, 42(3): 617-626.

[13]Owens D B, Capone F J, Hall R M, et al. Free-to-roll analysis of abrupt wing stall on military aircraft at transonic speeds. AIAA 2003-0750[R]. Reston: AIAA, 2003.

[14]Zhang Hanxin, Liu Wei, Xie Yufei, et al. On the rocking motion and its dynamic evolution of a sweep delta wing[J]. Acta Aerodynamica Sinica, 2006, 24(1): 5-9. (in Chinese)张涵信, 刘伟, 谢昱飞, 等. 后掠三角翼的摇滚及其动态演化问题[J]. 空气动力学学报, 2006, 24(1): 5-9.

[15]Ye Youda, Zhao Zhongliang, Tian Hao, et al. The stability analysis of rolling motion of hypersonic vehicles and its validations[J]. Science China, 2014, 57(12): 2194-2204.

[16]Liu Wei, Zhang Hanxin. Nonlinear dynamic analysis and simulation of wing rock for a slender wing[C]//Progress in Computation Fluid Dynamics-Proceeding of 12thChina Computational Fluid Dynamics Conference. Beijing: Aerodynamics Society of China, 2004: 370-376. (in Chinese)刘伟, 张涵信. 细长机翼摇滚的非线性动力学分析及数值模拟[C]//计算流体力学会议论文集. 北京: 中国空气动力学会, 2004: 370-376.

[17]Ma Baofeng, Deng Xueying, Rong Zhen, et al. The self-excited rolling oscillations induced by fore-body vortices[J]. Aerospace Science and Technology, 2015, 47: 299-313.

[18]Rong Zhen, Deng Xueying, Wang Bing, et al. Experimental investigation on flow characteristics during double limit cycle oscillation induced by forebody vortex[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(3): 20-24. (in Chinese)荣臻, 邓学蓥, 王兵, 等. 前体涡诱导双极限环摇滚流动特性的实验研究[J]. 实验流体力学, 2010, 24(3): 20-24.

[19]Zhang Jie, Cai Yi, Wu Jiali, et al. Research on a free-to-roll transonic test capability[J]. Acta Aerodynamica Sinica, 2016, 34(5): 611-616. (in Chinese)张杰, 才义, 吴佳莉, 等. 跨声速自由滚转试验技术研究[J]. 空气动力学学报, 2016, 34(5): 611-616.

[20]Sun Haisheng. Investigation on wing rock in low speed wind tunnel for a fighter configuration[J]. Experiments and Measurements in Fluid Mechanics, 2000, 14(4): 32-35. (in Chinese) 孙海生. 飞机机翼摇滚低速风洞实验研究[J]. 流体力学实验与测量, 2000, 14(4): 32-35.

[21]Wang Bing, Deng Xueying, Ma Baofeng, et al. An artificial transition technique applied to wing rock induced by forebody vortex[J]. Acta Aerodynamica Sinica, 2010, 28(5): 525-535. (in Chinese) 王兵, 邓学蓥, 马宝峰, 等. 前体涡诱导机翼摇滚的人工转捩技术研究[J]. 空气动力学学报, 2010, 28(5): 525-535.

[22]Shi Zhiwei, Li Luyang, Cheng Keming, et al. Wind-tunnel high attack angle dynamic testing device based on hybrid mechanism: China, CN101929915B[P]. 2011-11-30. (in Chinese)http://www.pss-system.gov.cn/sipopublicsearch/portal/uiIndex.shtml史志伟, 李鹭扬, 程克明, 等. 基于混联机构的风洞大迎角动态实验装置: 中国, CN101929915B[P]. 2011-11-30. http://www.pss-system.gov.cn/sipopublicsearch/portal/uiIndex.shtml

[23]Geng Xi, Shi Zhiwei, Cheng Keming, et al. A new hybrid mechanism for dynamic wind tunnel test of high maneuverable air vehicle[J]. Proc IMechE, Part G: J Aerospace Engineering, (Online) DOI: 10. 1177/0954410015620448

[24]Nelson R C, Pelletier A. The unsteady aerodynamics of slender wings and aircraft undergoing large amplitude maneuvers[J]. Progress in Aerospace Sciences, 2003, 39(2): 185-248.

[25]Katz J. Wing/vortex interactions and wing rock[J]. Progress in Aerospace Sciences, 1999, 35: 727-750.

[26]Wei Longkun, Ma Baofeng. Wing rock induced by a hemisphere-cylinder forebody[J]. Journal of Aircraft, 2014, 51(2): 606-613.

[27]Liu Wei, Yang Xiaoliang, Zhang Hanxin, et al. A review on investigations of wing rock problems under high angles of attack[J]. Advances in Mechanics, 2008, 38(2): 214-218. (in Chinese)刘伟, 杨小亮, 张涵信, 等. 大迎角运动时的机翼摇滚问题研究综述[J]. 力学进展, 2008, 38(2): 214-218.

[28]Tao Yang, Zhao Zhongliang, Yang Haiyong. Investigation on wing rock of wing-body configuration at high speed wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(6): 45-48. (in Chinese) 陶洋, 赵忠良, 杨海泳. 翼身组合体摇滚特性高速试验研究[J]. 实验流体力学, 2011, 25(6): 45-48.

[29]Takashi M, Shigeru Y, Yoshiaki N. The effect of leading-edge profile of self-induced oscillation of 45-degree delta wings. AIAA 2000-4004[R]. Reston: AIAA, 2000.

[30]Takashi M, Shigeru Y, Yoshiaki N. Data-based modeling of non-slender wing rock. AIAA 2003-738[R]. Reston: AIAA, 2003.

[31]Wei Dechen, Shi Zhiwei, Geng Xi, et al. Wind tunnel test for wing-body rock of canard-configuration aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(10), 3003-3010. (in Chinese)魏德宸, 史志伟, 耿玺, 等. 鸭式布局飞行器的翼体摇滚特性风洞试验[J]. 航空学报, 2016, 37(10): 3003-3010.

[32]Brandon J M, Nguyen L T. Experimental study of effects of forebody geometry on high angle of attack static and dynamic stability. AIAA-86-0331[R]. Reston: AIAA, 1986.

[33]Brandon J M, Nguyen L T. Experimental study of effects of forebody geometry on high angle of attack stability[J]. Journal of Aircraft, 1988, 25(7): 591-597.

[34]Vortex dynamics of free-to-roll slender and nonslender delta wings[J]. Journal of Aircraft, 2010, 47(1): 292-302.

[35]Grismer, Deborah S, Robert C N. Aerodynamics of a double delta wing undergoing pitching motions with and without sideslip. AIAA-94-1855[R]. Reston: AIAA, 1994.

[36]Grismer, Deborah S. An experimental study of the steady and unsteady aerodynamics of double delta wings for zero and non-zero sideslip[D]. Canada: The University of Notre Dame, 1995.

[37]Ross A J, Nguyen L T. Some observations regarding wing-rock oscillations at high angles of attack. AIAA-88-4371[R]. Reston: AIAA, 1988.

Effects of pitch angle on wing-body rock of canard-configuration aircraft

Wei Dechen, Shi Zhiwei*, Ang Haisong, Fu Junquan, Zhu Jiachen

(CollegeofAerospaceEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China)

To study wing-body rock of canard-configuration aircrafts, a model for wind tunnel test was designed having a chine forebody, canard wings, strake wings，main wings, and a vertical fin. This model was tested by different methods including free rolling motion, static force balance test, dynamic derivative test, and smoke wire technique. First, the complete rock process was studied by free-to-roll experiment in the range of pitch angelθ=12°～52° andΔ=1°. The results show that, rolling motions of the canard-configuration aircraft have several different mean roll angles and motion forms vary with different pitch angles. Second, the results of the static force balance test and dynamic derivative test confirm that the rolling motion can occur around zero or nonzero equilibrium roll angles with limit-cycle forms or nolimit cycle ones due to the influence of multi-vortex structures. Finally, the flow visualization tests show that the main vortices generate the wing-body rock at different stages. The possible mechanism for the wing-body rock was also analyzed for the canard-configuration aircraft.

canard wing; wing-body rock; nonzero equilibrium roll angle; non-limit cycle; flow visualization

0258-1825(2017)02-0198-07

2016-11-13;

2016-12-28

江苏高校优势学科建设工程资助项目

魏德宸(1986-),男,江苏徐州人,博士研究生,研究方向:飞行器大迎角气动特性,非定常空气动力学. E-mail: weimoving@163.com

史志伟*(1972-),男,教授. E-mail: szwam@nuaa.edu.cn

魏德宸, 史志伟, 昂海松, 等. 俯仰角对鸭式布局飞机摇滚运动的影响与机理分析[J]. 空气动力学学报, 2017, 35(2): 198-204.

10.7638/kqdlxxb-2016.0162 Wei D C, Shi Z W, Ang H S, et al. Effects of pitch angle on wing-body rock of canard-configuration aircraft[J]. Acta Aerodynamica Sinica, 2017, 35(2): 198-204.

V211.7

A doi: 10.7638/kqdlxxb-2016.0162