基于自适应滑模的侧窗制导控制一体化设计研究

沈昱恒,邱吉尔,张 迪,蔡云泽

(1.上海机电工程研究所,上海 201109; 2.上海交通大学 系统控制与信息处理教育部重点实验室,上海 200240)



基于自适应滑模的侧窗制导控制一体化设计研究

沈昱恒1,邱吉尔2,张 迪1,蔡云泽2

(1.上海机电工程研究所,上海 201109; 2.上海交通大学 系统控制与信息处理教育部重点实验室,上海 200240)

针对侧窗导弹末制导问题，提出了一种侧窗探测视场约束条件下的制导控制一体化设计方法。基于弹目相对运动模型分析了侧窗导弹运动规律，建立侧窗导引头探测视场角范围与导弹姿态角的约束关系，采用基于滑模控制理论的反步法设计导弹的制导控制一体化模型，给出了自适应滑模制导律：根据姿态角与侧窗视线角的约束关系，切换选择含约束和不含约束的自适应滑模控制。控制策略为：当弹目视线不满足侧窗探测范围约束时，在控制量中加入自适应俯仰角补偿项，使目标始终处于导弹侧窗视线范围内，解决了侧窗末制导过程中存在的目标跟踪视场角不对称约束问题；当弹目视线满足侧窗探测范围约束时，控制无需引入姿态角约束项，可直接应用自适应滑模控制律。仿真结果表明：在末制导过程中目标始终处在侧窗范围内，且对不同的初始条件有较好的鲁棒性。

侧窗导弹； 末制导； 制导控制一体化设计； 反步法； 自适应滑模； 弹目视线； 侧窗视线范围； 俯仰角补偿

0 引言

拦截弹高速飞行时与大气相互作用，在其周围形成复杂的流动结构产生的气动加热，使红外导引头探测到的目标图像出现偏移、模糊和抖动等问题，严重影响探测制导精度[1]。因此，美国THAAD系统中拦截弹导引头采用侧窗模式，有效减小了气动热影响，但同时单侧窗视场也限制了导引头的视线范围，导弹需实时调整弹道、导弹姿态，使目标始终在导引头探测视场内。在末制导过程中，经典方法是将制导与姿态控制分开设计，将姿态控制作为一阶延迟系统或固定时延，但侧窗约束的加入对导弹姿态角控制及控制响应时间提出更高的要求，因此一种可选的研究思路是考虑将导引和控制进行一体化设计[2-3]。

近年来，导弹制导和控制一体化问题引起了研究者的注意，但多数研究重点是改善姿态控制回路的响应时间，对侧窗提出的实时姿态角约束并未涉及[4]。文献[5]在制导控制一体化模型的基础上，采用零化脱靶量(ZEM)作为滑模面设计制导律；文献[6]采用反步法设计制导控制律，由在线神经网络估计系统的不确定性。在侧窗导弹研究中，文献[7]对侧窗约束建模，通过导弹滚转使目标在侧窗范围内，并通过调整俯仰角和偏航角使目标在侧窗最佳视线角，但该文仍是基于传统的设计方法将制导与姿态控制分开设计；文献[8]在将侧窗约束定义为攻角和侧滑角约束的基础上，研究了末制导中的制导控制问题，但该文设计制导律时仅考虑了终端视线角约束。为使导弹在末制导过程中能保证目标始终在侧窗范围内且命中目标，本文采用制导控制一体化设计理念，在分析建立侧窗视线约束与弹体姿态运动关系的基础上，采用自适应滑模和反步法，对一种满足侧窗姿态角约束的制导控制律设计进行了研究，并根据姿态角与侧窗视线角的约束关系，切换选择含约束和不含约束的自适应滑模控制，用末制导段数字仿真验证本文设计方法的有效性。

1 弹目相对运动模型

传统的导弹制导和控制系统是基于控制回路的时间常数要大于制导回路，从而将制导回路与控制回路分开设计：先根据弹目相对运动设计制导律，再设计姿态控制系统，使导弹的加速度跟上制导律，若整体的性能无法满足期望的要求，则重新设计。在侧窗探测末制导过程中，需实时快速调整弹道与姿态，分离设计造成的时延过大已不能满足要求，因此本文考虑采用制导控制一体化设计。

制导和控制一体化设计思路是对导引回路与姿态控制回路采用联合设计，在原理设计中，仍可在俯仰和偏航两个平面内分别进行，本文首先考虑俯仰平面内的设计。俯仰平面内弹目相对运动关系如图1所示。

根据文献[5]，导弹在俯仰平面导引控制一体化模型可描述为

(1)

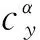
2 侧窗视线约束

为描述侧窗条件下导引头对目标的探测，定义弹体坐标系OV-XVYVZV、地面坐标系O-XYZ和侧窗坐标系OC-XCYCZC[8]。

a)O-XYZ系：原点O为地面发射点；OX轴在水平面内指向目标在地面的投影为正；OY轴与地面垂直向上为正。

b)OV-XVYVZV系：原点OV在导弹质心；OVXV轴与弹体纵轴重合，指向头部为正；OVYV轴在弹体纵对称平面内，垂直于OVXV轴；OVZV轴与OVXV、OVYV轴构成右手系。

c)OC-XCYCZC系:原点OC在导弹导引头回转中心；OCXC轴在弹体纵对称平面，与侧窗表面平行，指向弹头为正；OCYC轴在弹体纵对称平面，垂直于OCXC轴，向上为正；OCZC轴与OCXC、OCYC轴构成右手系。

为保证目标始终在目标的视线范围内，导弹有一个“抬头”或“低头”的趋势，其中“抬头”模式的二维示意如图2所示。

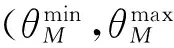
侧窗视线角约束即视线角∠ACT需在(qmin，qmax)范围内，由此要求导弹的俯仰角也在一定范围内，两者的转换关系如下。

步骤1)：计算点A，C在地面系中位置

(2)

(3)

将其从侧窗坐标系转换至弹体坐标系，有

(4)

(5)

式中：σC/V为OCXC、OVXV轴的夹角；XC，YC分别为目标在侧窗坐标系中的横纵坐标；[XC0YC0]T为侧窗中心在弹体坐标系中位置。

步骤2)：计算视线角和导弹姿态角的关系，有

(6)

3 自适应滑模变结构制导律设计

从上述导引控制一体化模型式(1)及侧窗约束关系可知：侧窗视线角约束下的制导控制问题是一个典型的高阶耦合非线性控制设计问题，因此考虑采用基于滑模控制理论的反步设计法，其过程如下。

(7)

(8)

式中：

反步设计法的要点是：针对非线性系统式(7)，将其分解为不超过系统阶数的子系统，然后从一个确定反馈和Lyapunov函数的子系统开始，设计中间虚拟控制量，再对虚拟控制量进行逐步修正直至全局输入。

制导律设计通常要求x1→0。因此基于反步设计，先针对第一个子系统，定义滑模

(9)

为保证系统状态能到达滑模面，且在达到滑模的过程中有优良的动态性能，可采用自适应趋近律

(10)

其物理意义是：当RTM较大时，适当降低趋近滑模的速率；当RTM→0时，使趋近速率迅速增大，保证视线角速率不发散[9]。

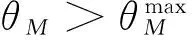
(11)

式中：p为姿态角约束的系数；ε1>0,k1>0。在式(11)中加入姿态角约束，目的是为在弹目距离接近过程中，逐渐增加姿态角约束的权重，保证目标在侧窗视线范围内。

然后针对第二个子系统，建立滑模面以保证第一个子系统的稳定

(12)

将式(11)、(12)代入第一个子系统，可得

(13)

并采用趋近律

(14)

则根据反步设计法，虚控制为

(15)

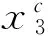
(16)

同样采用趋近律

(17)

式中：k3>0。则可得实际的控制表达式为

(18)

对式(18)，需证明其控制稳定性。选取Lyapunov函数

(19)

由式(11)、(13)可得

ε1sgn(s1)s1-k2(s2)2-k3(s3)2<0

(20)

由此可知，设计的式(18)控制可保证系统大范围渐进稳定。

4 仿真与分析

本部分将通过数字仿真验证控制方法的性能。设仿真条件为：设目标和导弹的初始位置分别为RM=[0 2 200]Tm，RT=[750 1 850]Tm，速度分别为vT=900 m/s，vM=1 032 m/s；目标初始弹道倾角为0°，目标的法向加速度为5g，导弹的弹道倾角为0°；侧窗的视线角范围以OCYC轴为中心±30°，即∠ACT∈[60°，120°]；r1=10，r2=8.15，∠AMC=10°，|ωz|≤150 (°)/s，|δz|≤45°。考虑“抬头模式”，若θmin<0°，则取θmin=0°，导弹的气动力参数见文献[11]。为降低滑模切换造成的控制抖振，用饱和函数

替代式(20)中符号函数sgns。此处：t=0.15。仿真所得拦截轨迹、侧窗视线角和俯仰角分别如图4～7所示。其中：图7为导弹初始姿态角不满足侧窗约束范围内时的姿态角变化。

由图5可知：在整个飞行过程中，实际目标视线一直保持在侧窗视线上下边界范围内。由图6可知：姿态角亦始终在上下限约束范围中。由图7可知：即使初始姿态角不满足侧窗探测要求，本文算法也能快速作出响应保证目标在侧窗范围内。

为进一步验证控制律的有效性和鲁棒性，将本文的控制策略与文献[10]的滑模导引律对比，进行蒙特卡罗打靶仿真。即保证其他条件相同情况下，设置以下场景。

a)场景1：导弹的初始攻角服从N(20°，(20°)2)的高斯分布，进行20次仿真验证在不同攻角情况下算法的鲁棒性。

b)场景2：目标初始位置从(750，1 850) m开始，每次间隔(50，0) m增加直至(1 200，1 850) m进行10次仿真，验证在不同的初始弹目相对位置情况下算法的适应性。

仿真结果见表1。

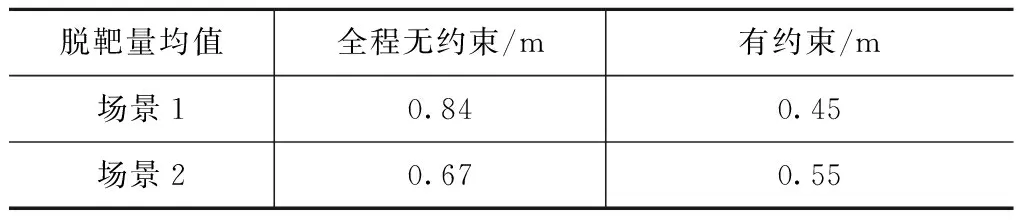
表1 有/无约束控制方法脱靶量均值Tab.1 Average miss distance of simulation between with/without constraint

由表1可知：本文设计的含姿态角约束的自适应滑模控制方法在满足侧窗约束的同时，脱靶量均值更小，精度更高。

5 结束语

导引头侧窗布局结构可有效降低红外头气动加热问题，也可作为新型多模复合导引头提供新布局设计思路，该技术在反导、反临近等高速、大机动目标拦截弹技术领域具有重要的工程应用价值。视场不对称约束问题是侧窗探测导弹末制导控制必须解决的问题。本文建立了导引头侧窗视线角与导弹姿态角约束关系，该方法可用于分析工程实际中各类工况弹道的侧窗姿态约束关系，指导制导控制律设计；获得了有姿态角约束的自适应滑模制导控制律。该方法采用一体化设计方法同时解决姿态角约束问题与快速性要求，仿真结果表明本文方法效果优于以往滑模制导律。本文研究可为侧窗导弹制导控制方法设计提供参考。在后续研究中，可在本文基础上对偏航通道引入后的侧窗一体化制导控制问题设计进行研究，解决工程化应用问题。

[1] 江涛, 丁明松, 高铁锁, 等. 高速平均流场对红外成像影响的计算分析[J]. 空气动力学学报, 2013, 31(6): 727-732.

[2] ZARCHAN P. Tactical and strategic missile guidance[M]. St. Louis: American Institute of Aeronautics and Astronautics, 2007.

[3] HOLLOWAY J, KRSTIC M. Predictor observers for proportional navigation systems subjected to seeker delay[J]. IEEE Transactions on Control Systems Technology, 2016, 24(6): 1-14.

[4] 姚郁, 郑天宇, 贺风华， 等. 飞行器末制导中的几个热点问题与挑战[J]. 航空学报, 2015, 36(8): 2696-2716.

[5] SHIMA T, IDAN M, GOLAN O M. Sliding-mode control for integrated missile autopilot guidance[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(2): 250-260.

[6] SHARMA M, RICHARDS N D. Adaptive, integrated guidance and control for missile interceptors: AIAA Guidance, Navigation, and Control Conference and Exhibit Providence[C]// Rhode Island: 2004.

[7] 支强, 蔡远利. 动能杀伤器侧窗定向机制分析及建模[J]. 西安交通大学学报, 2012, 46(1): 91-96+113.

[8] 徐龙. 侧窗探测下末制导段制导控制问题研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.

[9] 周荻. 寻的导弹新型导引规律[M]. 北京: 国防工业出版社, 2002.

[10] 苗昊春, 马清华, 陈韵, 等. 基于滑模控制的导弹制导控制一体化设计[J]. 弹箭与制导学报, 2011, 31(3): 6-10.

[11] 张保群. 导弹俯仰通道制导与控制一体化设计[D]. 哈尔滨: 哈尔滨工业大学, 2008.

Study on Integrated Guidance and Control Design for Side-Window Missile Based on Adaptive Sliding Modes

SHEN Yu-heng1, QIU Ji-er2, ZHANG Di1, CAI Yun-ze2

(1. Shanghai Electromechanical Engineering Institute, Shanghai 201109, China;2. Key Laboratory of System Control and Information Processing, Ministry of Education of China, Shanghai Jiao Tong University, Shanghai 200240, China)

An integrated design of guidance and control law under constrain of field-of-view angle (FOA) with side-window was put forward for terminal guidance of side-window missile in this paper. The motion law of the side-window missile was analyzed based on relative motion model between missile and target. The constrain of the FOA range and missile attitude angular was established. The integrated guidance and control mode was designed by the back stepping method based on sliding mode theory. The adaptive sliding mode law was given. The switching between the constrain adaptive sliding mode law and non-constrain adaptive sliding mode law was selected according to the constrain relationship of attitude angular and field-of-view angle of side-window. The control strategy was that the adaptive pitch compensation was added into the control to keep the target in the side-window range of the missile at all when the FOA of the missile and target did not meet the constrain of side-window detection range. It solved the problem of the asymmetrical constrain of target tracking FOA in the terminal guidance of side-window, and the adaptive pitch angular compensation did not need to add into the control which could apply the adaptive sliding mode law directly when the FOA of the missile and target met the constrain of side-window detection range. The numerical simulation results showed that the proposed solution could make the target in the side-window range in the terminal guidance, and it had good robustness under different initial conditions.

side-window missile; terminal guidance; integrated guidance and control design; back stepping method; adaptive sliding mode; FOA of missile and target; range of side-window; pitch compensation

1006-1630(2017)02-0061-06

2016-09-23；

2017-01-22

国家自然科学基金资助(61374160)；航空科学基金资助(20140157002)

沈昱恒(1983—)，男，博士，主要从事制导控制系统设计与研究。

TJ765.2

A

10.19328/j.cnki.1006-1630.2017.02.005