基于信号子空间估计的多基线InSAR干涉相位图滤波方法*
蒋 锐 龚清勇 朱岱寅 朱兆达
(1.南京邮电大学通信与信息工程学院,南京,210003; 2.南京航空航天大学雷达成像与微波光子技术教育部重点实验室,南京,210016)
基于信号子空间估计的多基线InSAR干涉相位图滤波方法*
蒋 锐1,2龚清勇1朱岱寅2朱兆达2
(1.南京邮电大学通信与信息工程学院,南京,210003; 2.南京航空航天大学雷达成像与微波光子技术教育部重点实验室,南京,210016)
多基线干涉合成孔径雷达(Interferometric synthetic aperture radar,InSAR)利用长短基线之间的关系,能够获得优于单基线InSAR的高程测量结果。本文针对多基线InSAR的数据特点,提出了基于信号子空间估计的多基线InSAR干涉相位图滤波方法。该方法将不同长度基线下所获得干涉相位图中同一像素单元信号作为一个训练样本,通过信号子空间的估计完成多基线InSAR干涉相位图滤波。仿真实验结果表明,本文方法可以在运算时间相当的情况下,获得优于回转均值滤波算法和回转中值滤波算法的滤波性能,是一种可满足实时处理要求的有效的多基线InSAR干涉相位图滤波方法。
干涉合成孔径雷达(InSAR);多基线;干涉相位图滤波;信号子空间;回转均值滤波
引 言
合成孔径雷达(Synthetic aperture radar,SAR)是现代高分辨率微波遥感成像雷达,具有与光学图像基本相当的图像分辨率。SAR可以对目标区域进行全天时、全天候的观测,因此随着SAR硬件及信号处理技术的不断发展,现已在军事和民用方面广泛应用[1-3]。干涉合成孔径雷达(Interferometric synthetic aperture radar,InSAR)对于同一观测区域进行多通道成像,并利用不同通道间干涉相位与测量目标高度间的关系,实现对于目标场景的三维成像[4-10]。传统的双通道InSAR系统仅仅包含两个通道,对目标高度的陡峭变化、噪声干扰较大以及获取具有相同斜距的散射点高度均无法得到满意结果。为了克服或减少这些问题带来的影响,近年来相关研究人员提出了采用多基线InSAR系统,根据长短基线各自的优缺点,充分利用长短基线之间的关系更加简单并且准确地估计出最长基线对应的干涉相位[11-14]。多基线InSAR系统的提出显著提高了对地形高程的测量精度。通过干涉相位图降噪滤波方法对干涉相位噪声进行有效的抑制,是确保后续获得高精度InSAR干涉处理结果的关键。相位滤波的方法必须确保相邻像素单元的干涉相位之间具有较强的相关性,并且相邻像素单元的噪声分布是统计独立的[15-18]。利用干涉相位对应的向量在复平面内连续变化的特点,最常用的滤波方法有回转均值滤波和回转中值滤波等[1]。由于在多基线干涉相位处理中存在多幅干涉相位图,本文提出基于信号子空间估计的多基线InSAR干涉相位图滤波方法。该方法充分利用多幅干涉相位图所提供的干涉信息,突破了传统相位滤波方法对于干涉相位图的假设限制,通过算法性能分析和仿真数据处理结果比较,证明本文方法相比于传统干涉相位图降噪滤波方法可以在不增加算法复杂度的条件下进一步提高滤波算法性能。
1 基于信号子空间估计的多基线InSAR干涉相位图滤波方法
1.1 算法原理
假设多基线干涉处理中存在K个基线,垂直于航迹方向有效基线长度分别为B1,B2,B3,…,BK,则存在一组对应的单基线干涉相位和一组模糊相位,即有
(1)
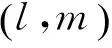
(2)

(3)
(4)
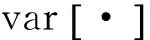
(5)
假设滤波窗口内邻近像素单元干涉相位变化忽略不计,定义样本协方差矩阵为
(6)
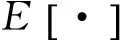
(7)
式中:I为单位矩阵;v为一个纯相位向量
(8)
该向量为协方差矩阵C最大特征值所对应的特征向量[19],即基于信号子空间估计的多基线InSAR干涉相位图滤波方法的滤波结果。
1.2 算法流程
基于信号子空间估计的多基线InSAR干涉相位图滤波方法流程如下。
(1) 根据K+1组天线接收回波信号,利用成像算法获得K+1幅SAR图像;
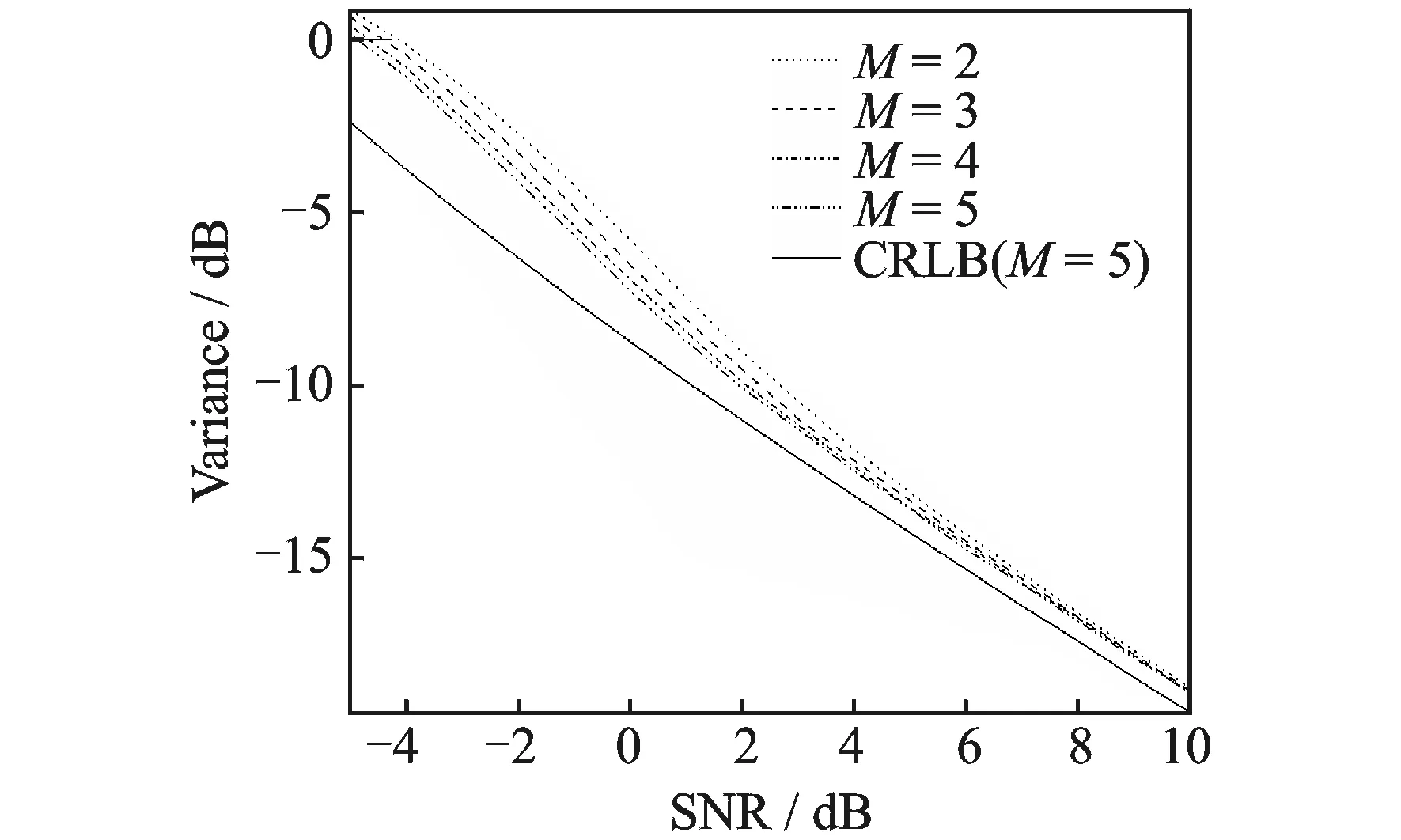
(2) 将K+1幅SAR图像分别进行图像配准、单基线干涉处理和去平地效应,获得K幅单基线干涉缠绕相位图,其分别对应有效基线长度为B1,B2,B3,…,BK,且假设B1 (3) 设置滤波窗口大小,根据式(6)构建样本协方差矩阵C; (4) 对样本协方差矩阵C进行特征分解,提取最大特征值对应的特征向量,即滤波窗口中心像素单元滤波后结果; (5) 按顺序使滤波窗口遍历干涉相位图,完成整幅干涉相位图的滤波处理。 1.3 算法性能分析 干涉相位滤波估计方差值的克拉默-劳界限(Cramer-Rao lower bound,CRLB)为[19-20] (9) 其中 (10) (11) M为多基线干涉处理过程中的天线数量,即当系统中总共存在K个基线时,有 (12) 式中:N为式(6)中滤波窗口内总的像素单元数;β为滤波窗口数据在方位数据域的信噪比(Signal-to-noise ratio,SNR),根据式(2~4),有 (13) 观察式(9),说明当多基线干涉处理过程中的基线个数越多,相对应的CRLB越小,则算法在达到CRLB时的算法性能就越好。 图1 蒙特卡罗仿真实验中干涉相位的估计方差值Fig.1 Variance of InSAR interferometric phase estimators from Monte-Carlo simulation 将图2(c-e)与图2(a)对比发现,当基线长度较短时,干涉相位图中干涉条纹较为简单,所观测地形地貌的变化相对于SAR图像的距离向和方位向采样间隔变化缓慢,利用3种滤波算法处理的结果基本相同。但是随着基线长度的不断增加,干涉相位的高程测量精度也不断提高,导致了干涉条纹越来越复杂。当基线长度为4倍最短基线长度时,干涉相位图的高程测量精度最高,此时地形地貌的变化相对于SAR图像的距离向和方位向采样间隔不再是缓慢变化的,在干涉条纹较为密集的区域利用传统回转均值滤波算法和回转中值滤波算法处理,会导致干涉条纹的严重失真。利用基于信号子空间估计的多基线InSAR干涉相位图滤波方法处理,可以有效降低噪声干扰对干涉相位图的影响,在干涉条纹较为密集区域也可以很好地保护干涉条纹,突破了传统干涉相位滤波方法对干涉相位图的假设限制,有效保证了后续高程测量的准确性。仿真实验结果表明,在多基线InSAR干涉处理过程中,本文所提出的基于信号子空间估计的多基线InSAR干涉相位图滤波方法具有更好的滤波性能,特别是针对较长基线对应干涉相位图,其算法性能优势尤其明显。 图2 仿真实验结果Fig.2 Simulation results 表1 3种干涉图滤波算法的执行时间 Tab.1 Execution time of the three filtering methods 由于回转中值滤波算法只需对滤波窗口内各像素单元的干涉相位值进行排序,选取中间值作为滤波结果,因此该算法的实际执行时间最短;而回转均值滤波算法需要对滤波窗口内各像素单元干涉相位值进行加权平均处理,虽然不需要复数乘法运算,但是其实际执行时间却比较长。因此3种滤波方法的实际执行时间相当,均可以满足算法的实时处理要求。 多基线InSAR干涉处理可以克服传统双通道InSAR处理的不足之处,利用长短基线之间的关系,提高高程测量精度。本文充分利用多幅干涉相位图的数据信息,基于信号子空间估计技术提出了一种新的多基线InSAR干涉相位图滤波方法。通过算法性能分析和仿真数据处理结果对比,表明基于信号子空间估计的多基线InSAR干涉相位图滤波方法可以有效利用多基线干涉处理中多幅干涉相位图的数据信息,突破传统干涉相位滤波方法对干涉相位图的假设限制,在不增加算法运算时间的条件下进一步提高滤波效果,特别是针对较长基线对应干涉相位图,其降噪滤波效果尤为明显,算法性能明显优于传统的回转均值滤波算法和回转中值滤波算法,是一种可满足实时处理要求的有效的多基线干涉相位图滤波方法。 [1] 保铮, 邢孟道, 王彤. 雷达成像技术 [M]. 北京:电子工业出版社, 2005. Bao Zheng, Xing Mengdao, Wang Tong. Radar imaging technology [M]. Beijing: Publishing House of Electronics Industry, 2005. [2] Ian G C, Frank H W. Digital processing of synthetic aperture radar data: Algorithms and implementation [M]. Boston: Artech House, 2005. [3] Charles V J, Daniel E W, Paul H E, et al. Spotlight-mode synthetic aperture radar: A signal processing approach [M]. Boston: Kluwer Academic Publisher, 1996. [4] Zebker H A, Golstein R M. Topographic mapping from interferometric SAR observations [J]. Journal of Geophysical Research Solid Earth, 1986, 91(B5): 4993-4999. [5] Golstein R M, Zebker H A, Werner L. Satellite radar interferometry: Two-dimensional phase unwrapping [J]. Radio Science, 1998, 23(4): 713-720. [6] Paul A R, Scott H, Ian R J, et al. Synthetic aperture radar interferometry [J]. Proceedings of the IEEE, 2000, 88(3): 333-382. [7] Wang Chisheng, Ding Xiaoli, Li Qingquan, et al. Equation-based InSAR data quadtree downsampling for earthquake slip distribution inversion [J]. IEEE Trans Geosci Remote Sens letters, 2014, 11(12): 2060-2064. [8] Heresh F, Falk A. DEM error correction in InSAR time series[J]. IEEE Trans Geosci Remote Sens, 2013, 51(7): 4249-4259. [9] Li F K, Golstein R M. Studies of multibaseline spaceborne interferometric: Synthetic aperture radars [J]. IEEE Trans Geosci Remote Sens, 1990, 28(1): 88-97. [10]蒋锐, 朱岱寅, 朱兆达. 目标高程对SAR图像中目标位置偏差的影响[J]. 数据采集与处理, 2013, 28(4): 425-430. Jiang Rui, Zhu Daiyin, Zhu Zhaoda. Effect of target height on target location displacement in SAR imagery [J]. Journal of Data Acquisition and Processing, 2013, 28(4): 425-430. [11]Michael S, Uwe S. Adaptive multilooking of airborne single-pass multi-baseline InSAR stacks [J]. IEEE Trans Geosci Remote Sens, 2014, 52(1): 305-312. [12]宋舒, 马仑, 廖桂生. 地球同步轨道双基SAR成像方法[J]. 数据采集与处理, 2013, 28(4): 410-415. Song Shu, Ma Lun, Liao Guisheng. Imaging algorithm for GEO-LEO biostatic SAR [J]. Journal of Data Acquisition and Processing, 2013, 28(4): 410-415. [13]Xie X M, Pi Y M. Multi-baseline phase unwrapping algorithm based on the unscented Kalman filter [J]. Let Radar Sonar Navigation, 2011, 5(3): 296-304. [14]Fornaro G, Monti G A, Pauciullo A, et al. Maximum liklehood multi-baseline SAR interferometry [J]. Let Radar Sonar Navigation, 2006, 153(3): 279-288. [15]Martinez C L, Fabregas X. Modelong and reduction of SAR interferometric phase noise in the wavelet domain [J]. IEEE Trans Geosci Remote Sens, 2002, 40(12): 2553-2566. [16]Liao G S, Li H. Estimation method for InSAR interferometric phase based on generalized correlation steering vector [J]. IEEE Trans Aerosp Electron Syst, 2010, 46(3): 1389-1403. [17]Bian Y, Mercer B. Interferometric SAR phase filtering in the wavelet domain using simultaneous detection and estimation [J]. IEEE Trans Geosci Remote Sens, 2011, 49(4): 1396-1416. [18]Li H, Liao G S. An estimation method for InSAR interferometric phase based on MMSE criterion [J]. IEEE Trans Geosci Remote Sens, 2010, 48(3): 1457-1469. [19]Charles V J, Daniel E W. Eigenvector method for maximum-likelihood estimation of phase errors in synthetic-aperture radar imagery [J]. Journal of the Optical Society of America, 1993, 10(12): 2539-2546. [20]张澄波. 综合孔径雷达:原理、系统分析与应用 [M]. 北京:科学出版社, 1989. Zhang Chengbo. Synthetic aperture radar: Theory, system analysis and application [M]. Beijing: Science Press, 1989. [21]Christian P R, George C. Monte Carlo statistical methods [M]. New York: Springer, 2004. [22]Yang J, Xi H S, Feng Y, et al. RLS-based adaptive algorithms for generalized eigen decomposition [J]. IEEE Transactions on Signal Processing, 2006, 54(4): 1177-1188. Novel Filtering Method of Multi-baseline InSAR Interferogram Based on Signal Subspace Processing Jiang Rui1,2, Gong Qingyong1, Zhu Daiyin2, Zhu Zhaoda2 (1.College of Telecommunications and Information Engineering, Nanjing University of Posts and Telecommunications, Nanjing, 210003, China; 2.Key Laboratory of Radar Imaging and Microwave Photonics, Nanjing University of Aeronautics and Astronautics, Ministry of Education, Nanjing, 210016, China) By utilizing the relationship of different baselines, the multi-baseline interferometric synthetic aperture radar (InSAR) can significantly enhance the capability of obtaining higher accuracy of the elevation measurement than that of traditional single-baseline InSAR. A novel filtering method of multi-baseline InSAR interferogram based on signal subspace processing is presented here. In the novel filtering method, we regard each pixel unit of different interferograms of different baselines as a training sample. Then the filter based on subspace tracking operation can effectively filtrate the noise interference of all the interferograms. Monte Carlo tests and simulated InSAR data validate that the new approach can achieve better filtering effect with similar levels of the execution time than the pivoting average-filter and the pivoting median-filter. interferometric synthetic aperture radar (InSAR); multi-baseline; interferogram filtering; signal subspace; pivoting average-filter 国家自然科学基金(61601243)资助项目;江苏省自然科学基金(BK20160915)资助项目;江苏省高校自然科学研究项目(14KJB510024)资助项目;雷达成像与微波光子技术教育部重点实验室开放课题(RIMP-2013001)资助项目;南京邮电大学科研基金(NY213009、NY214042)资助项目。 2015-01-06; 2015-11-12 TN9571.51 A 蒋 锐(1985-),男,博士,讲师,研究方向:雷达信号处理,E-mail: j_ray@njupt.edu.cn。 朱兆达(1939-),男,教授,中国电子学会会士、美国电气和电子工程师学会(IEEE)高级会员,研究方向:雷达信号处理。 龚清勇(1978-),女,博士,讲师,研究方向:动目标检测和雷达信号处理。 朱岱寅(1974-),男,博士,教授、博士生导师,IEEE会员,研究方向:雷达成像和信号处理方面的研究。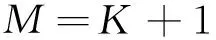
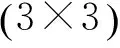
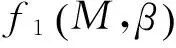
2 仿真实验结果
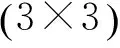

3 结束语





