基于HSMM和K-means的纳米孔多级事件检测

赖永杭, 颜秉勇, 王慧锋(华东理工大学信息科学与工程学院,上海 200237)

基于HSMM和K-means的纳米孔多级事件检测

赖永杭, 颜秉勇, 王慧锋
(华东理工大学信息科学与工程学院,上海 200237)

提出了一种基于隐半马尔科夫模型(HSMM)和K-means的混合算法,用于对纳米孔数据中出现的多级事件进行分析。通过K-means对检测到的阻断事件进行分析,确定纳米孔信号中的电流幅值水平个数,将其作为HSMM模型的隐状态输入;然后采用HSMM识别多级事件内部的不同水平,确定各水平的幅值和持续时间。最后将算法与Opennanopore软件进行比较,对三级、四级事件进行处理。仿真结果发现:HSMM比Opennanopore软件的准确率高,能够准确对事件进行分级。

纳米孔; HSMM; K-means; 多级事件

作为最具前景的第3代DNA测序技术,纳米通道检测技术在过去十年获得了巨大发展,被广泛用于生物化学研究,并已成为单分子检测必不可少的工具。在纳米通道检测技术中,由于纳米孔两侧电极施加电压的作用,待测分子在电场力作用下穿越纳米孔时,离子电流会被短暂阻断,这就达到通过外部设备检测电流变化来进行单分子检测的目的。阻断事件的持续时间、幅值和频率是纳米孔研究中的重要信息,这些参数已经被用来探究DNA、RNA和蛋白质等物质的生物物理学信息、物理化学信息和化学性质[1]。在DNA实验中,不同的碱基(A,G,C,T)通过纳米孔时的阻断事件幅值高度和持续时间是不同的[2],幅值变化范围为5～10 pA,持续时间范围为2～12 ms。

目前,纳米孔检测技术的研究热点主要集中在检测设备上,并已取得显著进展[3]。然而,对于纳米孔数据处理的研究却不够深入,大量的数据、复杂的信号使得纳米孔数据分析成为一个耗时和缺乏标准的过程[4]。Balijepalli等[5]开发的MOSAIC软件采用等效电路法对阻断事件进行建模分析。Arjmandi[3]研究了小波在低通滤波的优势,特别是在准确恢复阻断事件的持续时间和幅值当中的应用。Pedone等[6]对小分子(蛋白质、短DNA、RNA片段)实验中出现的持续时间小于100 μs的短事件进行了研究。

根据电流幅值水平个数,纳米孔阻断事件可分为2类:单级事件和多级事件。通常采用阈值法来检测阻断事件,然而阈值法只能确定事件的起始点和终止点,无法得到事件内部的子事件(即多级事件)的信息。Raillon等[7]开发的Opennanopore软件采用CUSUM算法来检测纳米孔多级事件,然而该方法对于参数选择敏感且准确度不高。只有精确检测出各种纳米孔电流信号,才能通过数据分析得到分子的动态和结构信息。

本文提出了一种基于隐半马尔科夫模型(Hidden Semi-Markov Model,HSMM)和K-means的纳米孔多级事件检测方法,用于对纳米孔信号的参数进行估计和信号的统计重构。该方法利用K-means确定纳米孔信号的最佳分类个数,将其作为HSMM隐状态的个数;采用HSMM模型对信号进行统计分析;在此基础上,对信号进行重构,得到理想的纳米孔多级事件。

1 纳米通道HMM分析

1.1 HMM模型

HMM (Hidden Markov Model)是一个双重随机过程,其中之一是Marcov链,它是基本随机过程,描述的是状态间的转移;另一重随机过程描述了状态和观测值之间的统计对应关系。

一个HMM过程可以由以下参数描述:

(1)N:模型中Markov链状态数目,记N个状态为θ1,…,θN,t时刻的Markov状态为qt,并且qt∈(θ1,…,θN)。本文中,N表示纳米孔多级事件的数目,N=2为单级事件,N>2为多级事件。

(2)M:每个状态对应的可能观测值数目,记M个观测值为V1,…,VM,t时刻的观测值为Ot,其中Ot∈(V1,…,VM)。

(3)π:初始状态概率矢量,π=(π1,…,πN),用于描述观测序列O在t=1时刻所处状态θi的概率。在纳米孔事件检测中,π是确定的,即没有分子通过纳米孔时的电流状态,其中

(1)

(4)A:状态转移矩阵,A=(aij)N×N,描述从状态i转移到状态j的概率,其中

(2)

(5)B:观测值概率矩阵,B=bj(yt),描述t时刻状态为θj条件下,观测值为yt的概率,其中

(3)

记一个HMM为λ=(N,M,π,A,B),或者简写为λ=(π,A,B)。

1.2 纳米通道HMM描述

纳米孔理想事件波形为幅值、持续时间均随机变化的矩形波,单级事件为仅有一个幅值水平的矩形波(除基线外),而多级事件则拥有多个幅值水平,类似“阶梯”状的矩形波。事件的每个幅值水平称为一个状态,1个事件至少拥有2个状态(基线值和事件值),各个状态之间的转移服从时间连续、状态有限的一阶Markov过程。结合纳米孔数据的特点,本文采用的Markov链如图1所示。

图1 纳米孔多级事件Markov链

由于检测池和信号传输过程中的噪声影响,状态间相互转移的Markov性不能直接显现出来,因此可以用HMM模型描述纳米孔检测信号。

(4)

式(4)中:i(t)为检测到的电流,即观测值;ibaseline(t)为带漂移的基线值;inoise(t)为信号噪声;ievent(t)为事件幅值,即隐状态,通过HMM模型判断t时刻的观测值Ot的隐状态,即可实现对纳米孔多级事件的识别。

通过分析发现,模型在状态θi(1≤i≤N)持续d个观测时间的概率为pi(d)=(aii)d-1(1-aii),结果为一个典型的指数分布且最大概率出现在d=0处。根据纳米孔阻断事件的信号特性,概率分布为指数分布是不合理的。

1.3 HSMM模型

为了克服常规HMM的缺点,HSMM在Markov链中加入状态驻留时间的非指数分布pi(d)。这时,隐状态的转移过程就成了半马尔科夫链,每个状态都有一个可变的持续时间分布[8],如图2所示。在这种情况下,状态之间的转移只有在通过pi(d)持续时间密度函数确定一个状态所发射的观测值数目后才会发生。

图2 半马尔科夫模型

HSMM与HMM相比,克服了因马尔科夫链假设造成HMM建模所具有的局限性,在解决现实问题中,HSMM提供了更好的建模能力和分析能力。实现HSMM模型主要有2种方法:

(1) 非参数方法,也是最直接的方法。在Markov链中,增加状态持续时间概率分布pi(d),d=1,…,D,其中D为所有状态可能停留的最长时间。

(2) 参数法,不去估计pi(d)的具体数值,而是假定pi(d)服从某种分布(如高斯分布、泊松分布等),通过估计描述这种分布的参数实现估计pi(d)的目的。

参数法计算量比非参数法大,而且假定pi(d)服从某种分布,并不适用于所有状态。因此,本文采用非参数法实现HSMM模型。

2 纳米孔多级事件检测

2.1 概述

利用HSMM对纳米孔信号进行统计分析,检测多级事件,即根据观测值序列OT=(o1,o2,…,oT)确定纳米孔的隐状态序列QT=(q1,q2,…,qT),然后根据隐状态序列确定各个事件的持续时间与幅值。其中,隐状态序列的确定是多级事件正确分级的关键。

分析过程主要涉及HSMM中的2个问题:学习问题,即HSMM的训练;解码问题,即通过HSMM模型和观察序列,确定隐状态序列。

2.2 HSMM模型训练

初始化:

(5)

递归:

(6)

初始化:

(7)

递归:

(8)

(3) 定义在给定观测序列O=(o1,o2,…,oT),t时刻,状态θm转移到状态θn的概率为

(9)

定义在t时刻,状态为θm且持续d个时间单位的概率为

(10)

定义在t时刻状态为θm的概率:

(11)

初始状态:

(12)

递归:

(13)

(4) 重估模型参数:

(14)

(15)

(16)

(17)

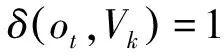
2.3 隐状态序列估计及事件信息确定

2.2节中,γt(m)为t时刻状态为θm的概率,欲获得最佳隐状态序列,即想获得t时刻可能性最大的状态,可对γt(m)取最大值,如式(18)所示:

(18)

隐状态序列确定后,可直接获得多级事件内部各子事件的持续时间,然而,子事件的幅值信息无法直接获得。在单级事件情况下,确定了事件的起始点和终止点后,幅值的选取主要有两种:对同一状态的所有观测值取平均值作为事件幅值;或取同一状态的最小观测值作为事件幅值。本文采用对事件内同一水平的数据点取平均值,作为子事件的幅值。

3 K-means算法确定隐状态个数

运用HSMM对阻断事件进行分析时,必须事先给定隐状态的个数N,即纳米孔事件幅值水平数目。若隐状态的个数判断错误,所得到的结果也是错误的。为了实现纳米孔事件的多级事件的自动检测,本文采用K-means聚类算法对数据进行分析,获得最佳分类个数k,将k值作为HSMM的隐状态个数。

K-means算法是一种聚类算法,常用于数据挖掘和模式识别中,是一种无监督学习式的算法。聚类分析的目的在于把数据集中的数据划分为一系列有意义的子集(或称类),使得每个子集中的数据尽量“相似”或“接近”,而子集与子集之间的数据尽可能有“较大差异”[10]。

假设有L个数据点{x1,x2，…，xL},需要分成K个类簇{μ1,μ2，…，μK},采用误差平方和准则函数作为K-means的目标函数:

(19)

其中:在数据点l被归类到类簇k时rlk为1,否则为0;xl为第l个数据点;uk为第k个类簇的中心点。直接通过寻找rlk和uk的方法来最小化J的值并不容易,通常采取迭代的方法。

(1) 先固定uk,选择最优的rlk,即将数据点归类到离它最近的中心就能使J取到最小值。

(20)

(2) 固定rlk,再求最优的uk。将J对uk求导且导数为0,可得到J最小时uk应满足:

(21)

即uk为类簇k中数据点的平均值。直到迭代前后J值相差小于一个阈值时,算法停止。

K-means由于其简单、快速的特点得到广泛应用。然而,K-means也有其自身的局限性,它需要使用者事先确定类簇的数目k[11]。k值的选取通常需要基于先验知识、假设和实际经验。但是,如果在不同的k下对聚类结果的质量进行评价,往往就可得到正确的k值。给定一个合适的簇指标,如平均半径和直径,当簇的数目等于或高于真实的簇的数目,该指标上升趋势会很缓慢,但是,一旦少于真实的簇数目时,该指标会急剧上升[12]。

本文选用数据点与所在类簇中心点的距离之和的平均值作为指标,用符号E表示,如式(22)所示。经仿真实验和实际信号检验,可以准确确定纳米孔事件的级数。

(22)

其中,Q为最大类簇个数。

4 基于K-means和HSMM的纳米孔事件检测

基于HSMM和K-means的纳米孔事件检测算法主要包括3个部分:事件检测、事件级数判断、事件分析。

(1) 事件检测。纳米孔数据的分析从在含有噪声的基线电流中判断阻断事件开始,目前,普遍采用阈值法来分离事件,在该方法中,如果电流超过所设阈值则为事件。阈值定义为峰值检测因子与噪声均方根σ的乘积。峰值检测因子的选择要尽量满足两个条件:一是数值尽可能大,以减少将噪声误判为事件的数量;二是数值尽可能小,以尽可能多地检测到阻断事件。通常阈值为偏离基线电流的5倍的噪声均方根[13]。

检测到事件发生时,分别将下降沿和上升沿中第1个穿越基线电流的点作为起始点和终止点。为了便于观察和分析,本文在事件前后各增加50个采样点。

(2) 事件级数判断。通过K-means算法判断事件最佳分类数目N,即纳米孔电流幅值水平个数。

(3) 事件分析。对于单级事件,即N=2时,可以通过传统方法确定事件的起始点和终止点,进而得到事件的持续时间和幅值,而不必通过HSMM算法处理,提高算法处理速度。当N>2,即事件为多级事件时,传统方法失效,引入HSMM模型对事件进行分析。该步骤的主要目的是确认事件的持续时间、幅值。系统结构框图如图3所示。

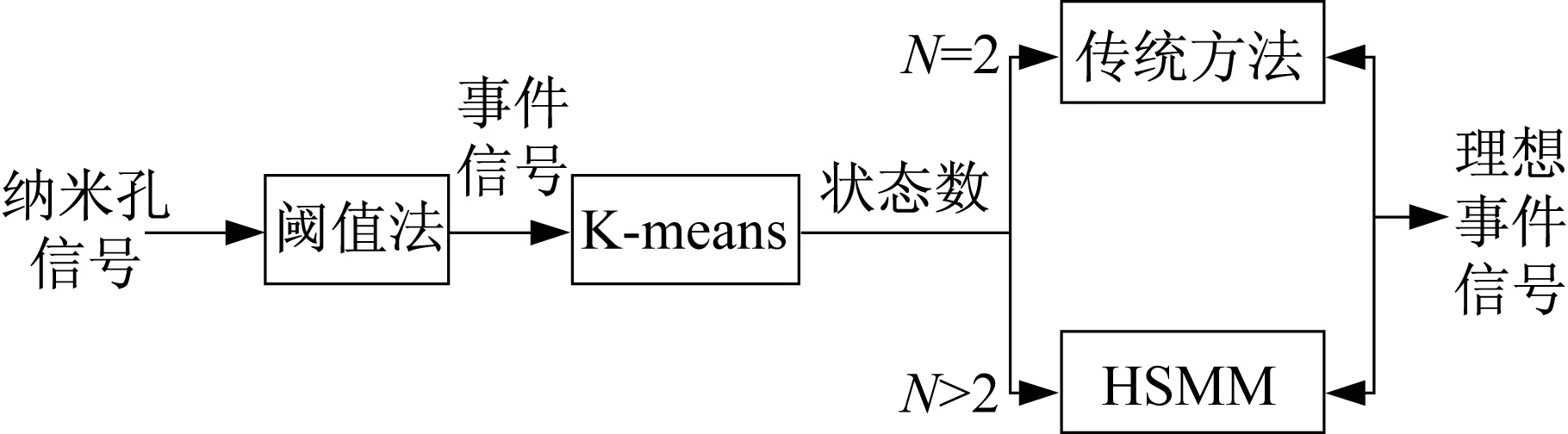
图3 系统框图

5 仿真实验与结果

5.1 实验平台与仿真数据生成

实验采用α-Hemolysin生物纳米孔,缓冲液由10 mmol/L Tri-HCL (pH=7.8)配置。在检测池两端置入Ag/AgCl电极,实验过程中施加100 mV电压。信号采用ChemClamp(Dagan Corporation公司)电流放大器对纳米孔的离子电流进行检测和放大，放大后的信号经过3 kHz的滤波后,选用DigitalData 440A数模转换器(Axon Instruments公司)进行采样,采样频率为250 kHz。

利用纳米孔在检测池中无待测分子时采集7 000个数据点,采样频率为250 kHz,将该信号作为背景噪声,其均值为100.115 6 pA,方差为1.649 6,由式(4)可知,此时的数据为基线电流与噪声之和,如图4(a)所示。在纳米孔实验中,多级事件主要为三级和四级事件,因此本文采用这2种事件来检测算法的有效性。根据实际纳米孔实验信号幅值高度和持续时间特征,取其中较为典型的多级事件信号,产生一个采样点为7 000的模拟纳米孔理想信号,信号中包括单级事件和多级事件,如图4(b)所示。将两个信号叠加,得到模拟实验仿真信号,如图4(c)所示。

图4 模拟纳米孔实验信号

5.2 仿真结果与对比

首先通过阈值法,检测是否有阻断事件发生,本文中,阈值设置为偏离基线值10 pA。检测到事件发生后,确定事件的起始点和终止点。下一步通过K-means算法判断事件的级数,结果如图5所示。

图5中,二级事件(包括基线)即为单级事件,曲线变化不大,几乎成一条直线；三级事件在类簇个数为3时指标骤降,而后趋于平稳；四级事件也在类簇个数为4时指标骤降。可见,K-means可以准确判断事件级数,可以用于纳米孔多级事件的自动判定,无须先验知识。

K-means正确判断事件级数后,当最佳类簇个数为2时,即为单级事件,则由传统算法处理。若最佳类簇个数大于2,即为多级事件,则由HSMM算法处理。

在纳米孔数据分析中,采用直方图来分析事件峰值,对直方图进行高斯拟合后可以得到事件各级的幅值。由图6(a)所示,事件有3个幅值水平,幅值分别为:99.69,70.12,59.97 pA。通过图6(b)示出的处理效果对比图可看出,HSMM方法处理后的事件曲线几乎和理想曲线重合,数据点误判概率接近0,幅值高度误差为0.14～0.32 pA。而CUSUM(Cumulative Sum)算法的处理效果显示,算法对事件错误分级,且出现了不少“毛刺”,数据点错判概率为9.8%。

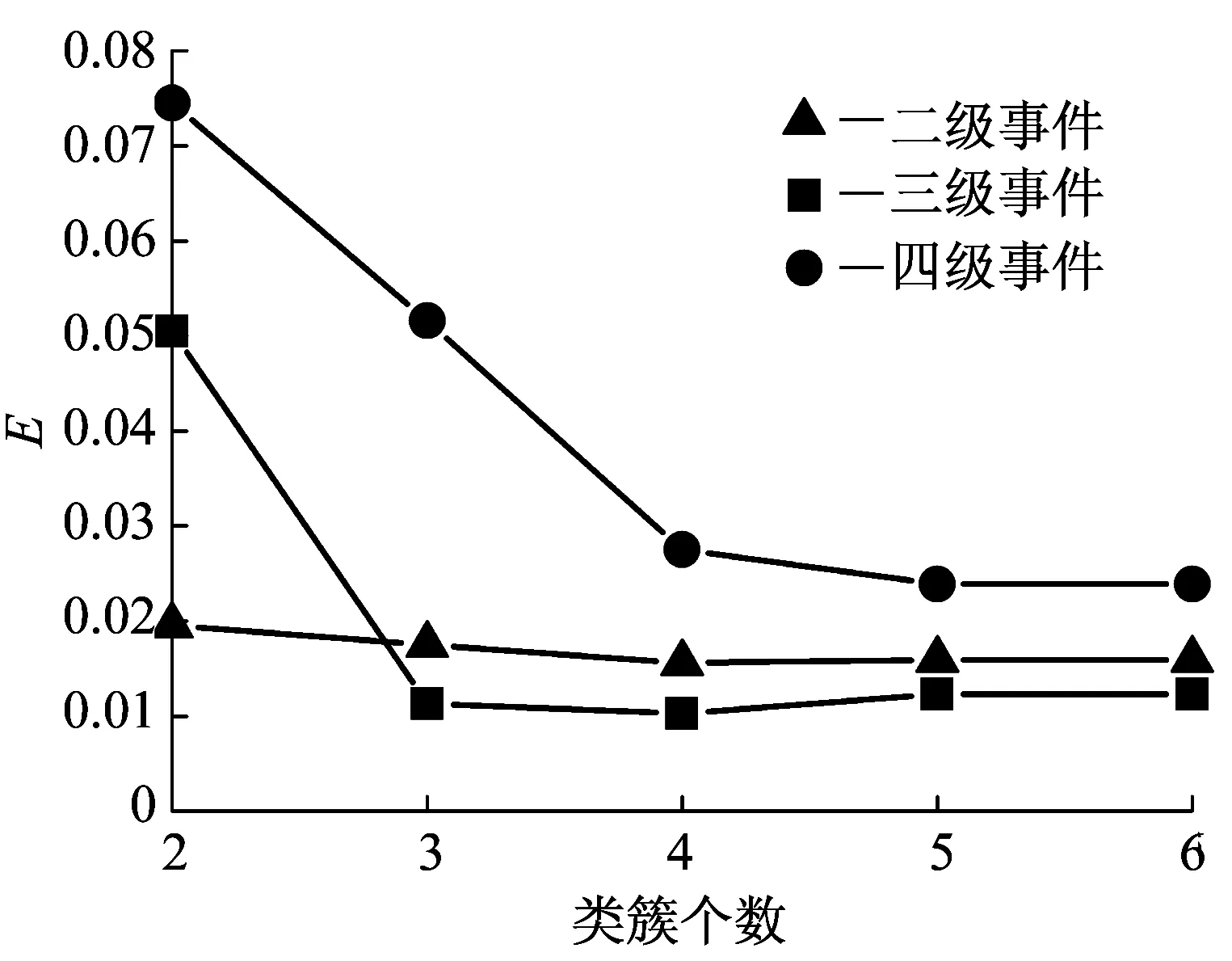
图5 事件级数判断

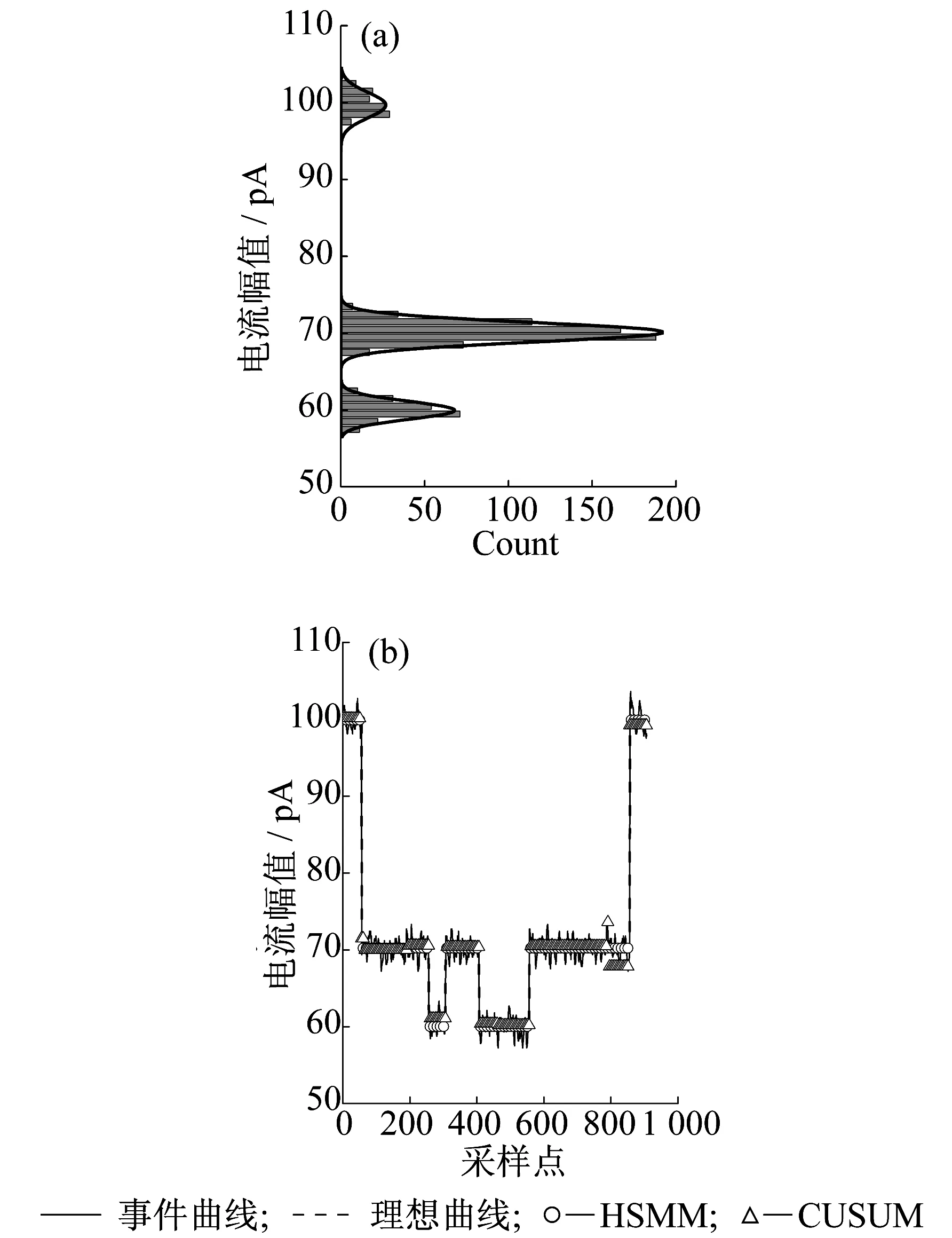
图6 三级事件

四级事件的处理效果对比如图7所示。图7示出了直方图高斯拟合后有4个峰值:100.04,70.07,65.27,60.49 pA。由图7(b)示出的处理效果比较可见,HSMM处理的曲线与理想曲线几乎重合,数据点错判概率接近0,幅值高度误差为0.01～0.19 pA。CUSUM算法的数据点错判概率为11.9%,幅值高度误差为0.17～1 pA。

图7 四级事件

6 结束语

采用HSMM和K-means聚类算法,有效地解决了纳米孔实验中出现的多级事件识别问题,实现了多级事件的自动检测分析。由仿真信号实验结果可得,该算法与Opennanopore软件的CUSUM算法相比,算法精度高,能够实现纳米孔事件的正确自动分级,因此可以用于纳米孔多级事件分析。

[1]GU Z,YING Y L,CAO C,etal.Accurate data process for nanopore analysis[J].Analytical Chemistry,2015,87(2):907-913.

[2]CLARKE J,WU H C,JAYASINGHE L,etal.Continuous base identification for single-molecule nanopore DNA sequencing[J].Nature Nanotechnology,2009,4(4):265-270.

[3]ARJMANDI N,ROY W V,LAGAE L,etal.Improved algorithms for nanopore signal processing[C]∥Nanopores for Bioanalytical Applications Proceedings of the International Conference.[s.l.]:[s.n.],2012:11-17.

[4]ZHANG N,HU Y X,GU Z,etal.An integrated software system for analyzing nanopore data[J].Science Bulletin,2014,59(35):4942-4945.

[5]BALIJEPALLI A,ETTEDGUI J,CORNIO A T,etal.Quantifying short-lived events in multistate ionic current measurements[J].Biophysical Journal,2011,106(2):637-643.

[6]PEDONE D,FIRNKES M,RANT U.Data analysis of translocation events in nanopore experiments[J].Analytical Chemistry,2009,81(23):9689-9694.

[7]RAILLON C,GRANJON P,GRAF M,etal.Fast and automatic processing of multi-level events in nanopore translocation experiments[J].Nanoscale,2012,4(16):4916-4924.

[8]YU S Z.Hidden semi-markov models[J].Artificial Intelligence,2010,174(2):215-243.

[9]YU S Z,KOBAYASHI H.An efficient forward-backward algorithm for an explicit-duration hidden Markov model[J].IEEE Signal Processing Letters,2003,10(1):11-14.

[10]李双虎,王铁洪.K-means聚类分析算法中一个新的确定聚类个数有效性的指标[J].河北省科学院学报,2003,20(4):199-202.

[11]NALDI M C,CAMPELLO R J G B,HRUSCHKA E R,etal.Efficiency issues of evolutionary K-means[J].Applied Soft Computing,2011,11(2):1938-1952.

[12]RAJARAMAN A,ULLMAN J D.大数据-互联网大规模数据挖掘与分布式处理[M].北京:人民邮电出版社,2012:188-189.

[13]PLESA C,DEKKER C.Data analysis methods for solid-state nanopores[J].Nanotechnology,2015,26(8):2890-2898.

Detecting of Multi-level Events in Nanopore Experiments Based on HSMM and K-means

LAI Yong-hang, YAN Bing-yong, WANG Hui-feng

(School of Information Science and Engineering,East China University of Science and Technology,Shanghai 200237,China)

This paper proposes a HSMM and K-means based hybrid algorithm for identifying the multi-level events in nanopore data.By means of K-means to analyze the detected blockade events,the number of current amplitude level of nanopore data can be identified,which will be taken as the input of the HSMM’s number of hidden states.And then,HSMM is used to identify different level inside multi-level event and deceide the dwell times and amplitude of different levels.In the situation of third-level and fourth-level event,the simulation results show that HSMM is more accurate than Opennanopore software,and can classify the events accurately.

nanopore; HSMM; K-means; multi-level events

1006-3080(2017)02-0220-07

10.14135/j.cnki.1006-3080.2017.02.011

2016-07-11

国家重大仪器专项(21327807)

赖永杭(1991-),男,硕士生,主要研究方向为检测技术与自动化装置。

王慧锋,E-mail:whuifeng@ecust.edu.cn

TH776

A