RTM中纤维结构对树脂浸渍影响的数值模拟

周云飞, 方 荀, 王文琪, 郭卫红, 戴干策(华东理工大学化学工程联合国家重点实验室,上海 200237)

RTM中纤维结构对树脂浸渍影响的数值模拟

周云飞, 方 荀, 王文琪, 郭卫红, 戴干策
(华东理工大学化学工程联合国家重点实验室,上海 200237)

在树脂传递模塑成型(RTM)中,缩减充模时间以及降低气泡含量是该工艺不断完善的两个关键。本文以牛顿流体为基础,结合Navier-Stokes方程组,构建了二维双尺度气液两相流模型。采用有限体积法(FVM)求解计算域流场物理量,并利用流体体积(VOF)界面追踪技术实现了等温充模阶段的模拟。综合分析了充模阶段流场物理量的变化情况,研究了纤维结构以及树脂黏度对充模时间以及气泡形成与排除的影响,并与分析结果和实验结果进行对照,吻合度较高。数值计算结果表明,二维双尺度模型能准确反映树脂的充模过程。对于低黏度熔体,编织纤维的横纵向孔隙宽度均有一个最佳尺寸,此外,树脂黏度的增加会影响气泡在纤维中的形成以及排除过程,从而影响最终的充模时间。

充模时间; 数值模拟; FVM; VOF; 纤维结构

树脂传递模塑成型(RTM)由于在树脂基复合材料制备中具有成本低廉、性能优异、增强材料含量高等突出优势,得到了广泛的应用[1]。此外,RTM在大型制品与复杂结构的制备方面表现出的可设计性,以及在闭模情况下不释放有害气体的环保性,使得它越来越受到相关行业(汽车、航天等)的青睐。

RTM基本由两个步骤组成[2]:首先将树脂注入预先放置有增强材料(纤维毡、编织纤维等)的模腔内;然后在特定温度以及压力条件下使树脂固化。此外,RTM工艺有两个基本问题:树脂浸渍时间以及制品气泡含量,后者尤为重要。据文献报导,气泡含量每增加1%,制品性能(主要为拉伸强度与层间剪切强度)则下降大约10%[3]。由于树脂对增强材料的浸渍效果取决于两者物性、树脂/纤维表面能、接触时间等众多因素,因此实验研究如何改善RTM工艺十分耗时、耗力,也不经济。随着计算机技术的发展,如今数值模拟成了RTM研究领域较为常用的方式[4]。先前已有不少研究人员针对浸渍时间以及气泡含量,从模型、数学方法等方面着手,使数值模拟在更贴近实际的情况下,探讨如何改善上述两个问题。

Zhang等[5]采用单相流模型,不考虑内部空气流动的情况,以相对简单的模型对RTM工艺中的树脂流动进行了数值模拟,分析了速度、纤维含量、进口数目、位置以及出口数目对工艺的影响。Echchelh等[2]则认为在不影响制品质量情况下减少树脂浸渍时间依然是RTM工艺中最为重要的一环,而不恰当的注射方式往往导致产生更多的气泡以及增强材料的变形,他们通过有限元/控制体积(FE/CV)方法,深入研究了填充过程中的一系列影响参数,并与分析结果对照,两者十分接近,以数值模拟的方式成功优化了RTM工艺的循环时间。此外,Park等[6]针对LCM中树脂在编织纤维中的非饱和浸渍进行了实验与模拟,观察到明显的“指形流”,认为毛细管数是气泡产生以及排除的重要参数,同时在数值模拟方面,指出毛细作用力或表面张力可以使计算更为精确。在此基础上,Yang 等[7]提出树脂在纤维束内束间流动的不均一性是造成气泡滞留的首要原因,并提出对称模型,在束内使用Brinkman方程,束间采用Stokes方程,通过VOF追踪树脂流动前沿,以此研究了树脂在束内、束间流动时的相互关系。Padaki等[8]对铺有多层纤维织物的RTM进行数值模拟,在与实验结果比较后提出交织指数对充模时间有显著影响,交织指数越高,充模时间越长,并提出两者间的数学公式作为参考。另外结合计算方法的优化,Chen等[9]在简化运算后,利用两个线性方程,预测了RTM工艺中简单模腔的注射口对充模时间的影响。Advani等[10]提出串联优化算法,以流动前沿为参照,并在虚拟加工环境中进行验证,优化了RTM工艺的树脂进出口位置。文献[11]结合半经验公式,对尼龙6结构反应注射成型过程进行了计算模拟,在优化进出口位置设计基础上,提出最佳入口参数(如速度值)来达到减少充模时间与气泡含量的目的。国内研究者如李海晨等[12]则是利用达西定律,并以此为基础建立树脂流动控制方程,结合贴体坐标法与有限差分法对树脂浸渍进行了模拟,获得了树脂流动前沿和压力场分布,确定了排气口位置以及树脂浸渍时间。Porto等[13]在RTM基础上提出了LRTM工艺,并运用FLUENT以及PAM-RTM两款软件对这两种工艺进行数值模拟,比较后得出LRTM在整体浸渍时间上有绝对优势。

虽然近几十年来,国内外研究人员对RTM工艺的数值模拟做了大量的研究,但是多数研究者将工艺简化为牛顿流体在均匀多孔介质内的浸渍流动,在此基础上通过改变工艺参数或是模腔结构,从宏观上优化工艺,使充模时间减少,制品气含量降低。然而,关于纤维结构本身在RTM工艺中对树脂浸渍的影响研究相对较少。本文着重考虑纤维结构的影响,简化后提出了二维双尺度结构模型,从分析与实验两方面数据进行数值模拟验证,揭示了纤维结构对树脂浸渍时间以及气泡的产生与排除过程的影响,并进一步研究了树脂黏度对其浸渍速率的作用。

1 模型与方程

1.1 物理模型

一般编织纤维结构如图1所示,主要由纬向纤维束与经向纤维束相互交叉编织而成。通常纤维束与纤维束之间无法紧密结合,存在一定孔隙,与纤维束内孔隙相比,其量级尺度较大,故称之为大孔隙通道。

图1 编织纤维结构局部图

本文提出的二维双尺度模型如图2(a)所示,其中实线填充区域分别为纬向纤维束与经向纤维束,其余为束间大孔隙通道,分成与纬向纤维束平行的横向通道以及与经向纤维束平行的轴向通道。二维双尺度模型以实际编织纤维结构为基础,截取其中一个“单元”作为研究对象,其中纬向纤维束长9 mm,宽6 mm;经向纤维束长6 mm,宽3 mm。另外,纤维束间孔隙又分为轴向孔隙宽度WA与横向孔隙宽度WT。相应的树脂浸渍预测如图2(b)所示。

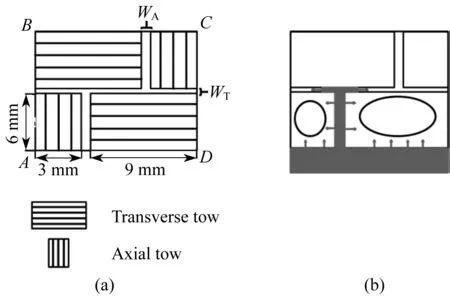
图2 二维双尺度模型(a)与树脂浸渍预测(b)

1.2 纤维束渗透率

在二维双尺度模型中,纤维束区域为多孔介质区,其中渗透率分为横向渗透率K⊥(垂直于纤维取向)与轴向渗透率K//(平行于纤维取向),其余区域为空气填充区域。根据文献[14]的研究,横向渗透率与纤维丝半径r以及纤维束孔隙率ε的关系可由式(1)与式(2)表示:

(1)

而l与孔隙率ε有关:

(2)

纵向渗透相较横向渗透而言,过程相对简单,其表达式[15]如下:

(3)

其中c为常数,对于截面为六边形排列的纤维束,c=53。

1.3 边界条件及模拟预测

边界条件的设定是数值模拟的重要一环。本文模拟条件下的树脂黏度较低,实验中在真空泵协助下即可将树脂注射入模腔中,故采用压力驱动的方式,模型中将树脂入口AD边设置为压力入口(p=p0),BC边设置为压力出口(p=0)。此外,由于模型为“单元”模型,在纤维结构中具有代表性,理论上AB边与CD边上的动量变化为零,因此将两边设置为对称边界。

由于纤维束内存在多孔介质黏性阻力,而束间孔隙通道阻力较小,故预测树脂在孔隙间运动速度会高于束内,如图2(b)所示,树脂在接触到纤维束与孔隙通道后,由于两者运动速度存在差异,树脂会“优先”进入孔隙通道,这样就会对图中椭圆区域形成气泡裹挟。裹挟的气泡要么被周围树脂不断挤压变小,要么随着后续树脂的推动也不断随着树脂运动,但基本以后者为主。然而,在运动过程中,由于运动途径不一致,气泡会分裂,这对充模时间以及最终制品的质量是一个考验,而气泡的运动主要与纤维结构有关。因此纤维结构中孔隙通道的大小在树脂浸渍的过程中起着关键作用。

1.4 模型方程与计算方法

在单尺度的RTM数值模拟中,常常把树脂在纤维束中的流动简化成牛顿流体在多孔介质中的流动,并且为了顺利进行数值模拟,做出以下假定:纤维束为刚性多孔材料,树脂浸渍不会造成其变形;树脂不可压缩;与黏性力相比,不考虑惯性力与毛细作用力。基于上述简化以及假定,可知流动符合Darcy定律,用其描述动量守恒,动量守恒方程可表示为

(4)

结合连续性方程,转化为式(5):

(5)

然而,在本文的双尺度模型中,毫米级的束间孔隙尺度与微米级的束内孔隙尺度相比,存在几个量级的差别,并不能简单地用单尺度模型描述,其流动方程也不能完全用Darcy定律描述。针对树脂在束间的宏观流动,Tan等[16]提出添加非零源项Sm,具体如下式:

(6)

式(6)中Sm可利用式(7)通过体积平均法求得,式(7)中V为平均化体积,n为树脂相法向向量。

(7)

对于束内的微观流动,由于纤维不会吸收树脂,故整体依然可以看成流体在多孔介质内的流动,符合Darcy定律。

此外,本文中RTM模拟涉及两相流,分别为树脂相与空气相,利用VOF[7]进行树脂流动前沿追踪。在二维计算域中,对于每个控制体,黏度和密度的计算方法为

(8)

(9)

体积分数(α)定义:

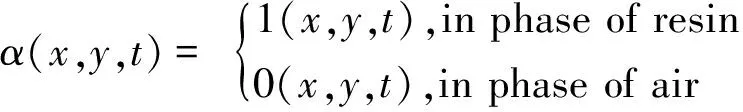
(10)

在两相界面处,0<α<1。树脂体积分数守恒方程为

(11)

2 计算验证

2.1 概述

为验证计算的可靠性以及有效性,本文先研究了RTM中的两个基本问题[17]:轴向流和径向流,并将FLUENT计算所得结果与分析结果进行比较,分别从一维和二维两个方面对该计算方法进行验证,确保得到有效的结果。此外,也将二维双尺度模型计算结果与文献实验结果进行比较,发现两者发展趋势基本保持一致。

2.2 轴向流

在轴向流验证中,树脂通过恒压线性注射从左侧进入矩形模腔,如图3所示,具体参数见表1。由于注射口宽度与模腔宽度相同,使得流动前沿垂直于左、右壁面直线推进,所以将此例视为一维流动问题。同时,由于计算区域的规整性,通过结构化网格对其进行离散。

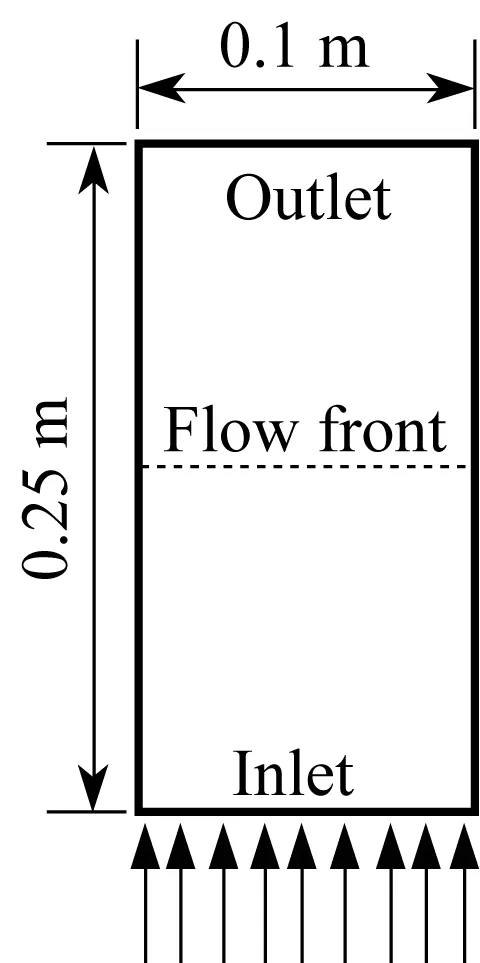
图3 轴向流示意图

在恒压注射条件下,树脂流动前沿距离(xf)随时间的变化可以通过解析方法获得:

(12)

图4将解析得到的树脂流动前沿位置与由FLUENT数值模拟得到的前沿位置进行了比较,同时也验证了网格无关性。由图4可知,随着网格数目的增加,数值模拟得到的结果越来越精确,同时与解析解符合程度不断提高,当网格数为25 400个时(网格尺寸为0.5 mm2),数值模拟与解析解的结果基本一致,说明该条件下数值模拟结果可靠。

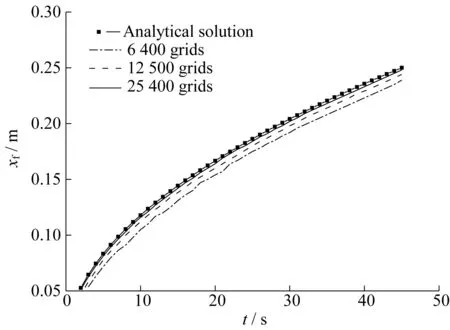
图4 轴向流网格无关性以及数值模拟验证

2.3 径向流

在径向流验证中,树脂在恒定压力p0作用下由几何中心点注入,如图5所示。此例是二维流动问题,树脂流动前沿处渗透率在各个方向上均相同。树脂与增强体的物理性能以及注射压力与上例相同,具体如表1所示。

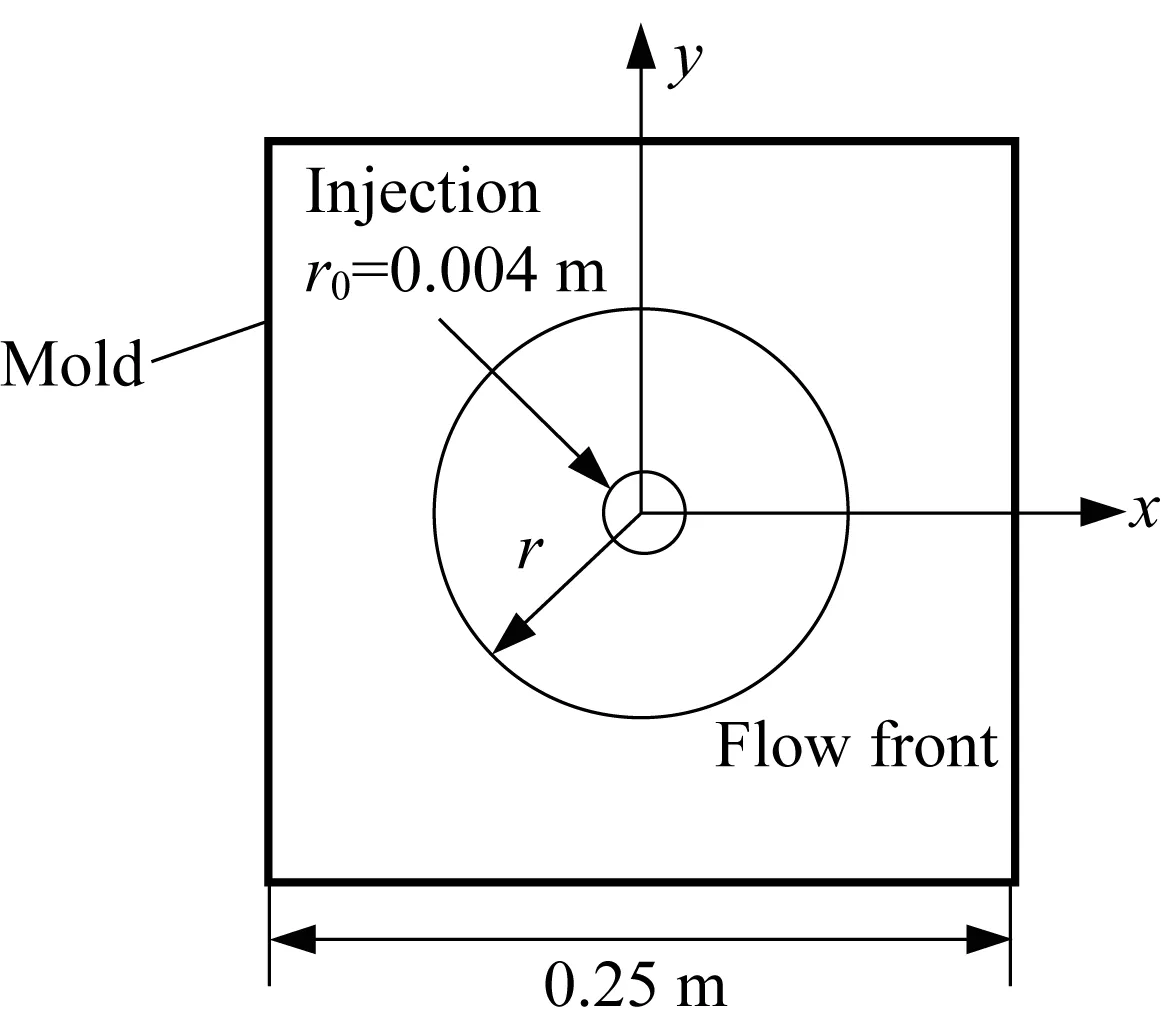
图5 径向流示意图

μr/(Pa·s)ρ/(kg·m-3)v/(m·s-1)εK/m2μa/(Pa·s)0．069600．50．65×10-101．8×10-5

由于计算区域不规则(中心挖去了半径极小的圆),因此采用非结构性网格(三角形)对其进行离散。图6所示为径向流数值模拟结果与分析结果的比较,分析解计算式如下:

(13)

图6 径向流网格无关性及数值模拟验证

从图6可以看出,与上例相似,数值模拟得到的结果与分析解相近,而且随着网格尺寸的不断细化,与分析解不断逼近,几乎重合。

2.4 实验验证

以上两例皆反映了CFD计算对网格细密要求的依赖,因为在VOF方法中,需要利用有限体积法同时求解非线性偏微分方程,因此对网格尺寸有所要求。此外,计算结果与分析解的对照说明了该计算方法的可靠性以及有效性。因此,本文运用相同的计算方法对二维双尺度模型以及所设定边界条件进行验证,具体参数见表2。

计算结果如图7所示,与文献[18]中实验结果趋势基本一致。以恒定速度注射,入口压力变化可分为4个阶段:(Ⅰ)树脂开始浸渍,由于流动阻力的存在,可观察到压力是非线性变化,可由达西定律预测[19];(Ⅱ)可发现压力是线性变化,主要为大孔隙通道的单尺度浸渍;(Ⅲ)压力增加为树脂浸渍编织纤维造成;(Ⅳ)浸渍接近饱和后,压力趋于稳定。

表2 实验验证各项参数

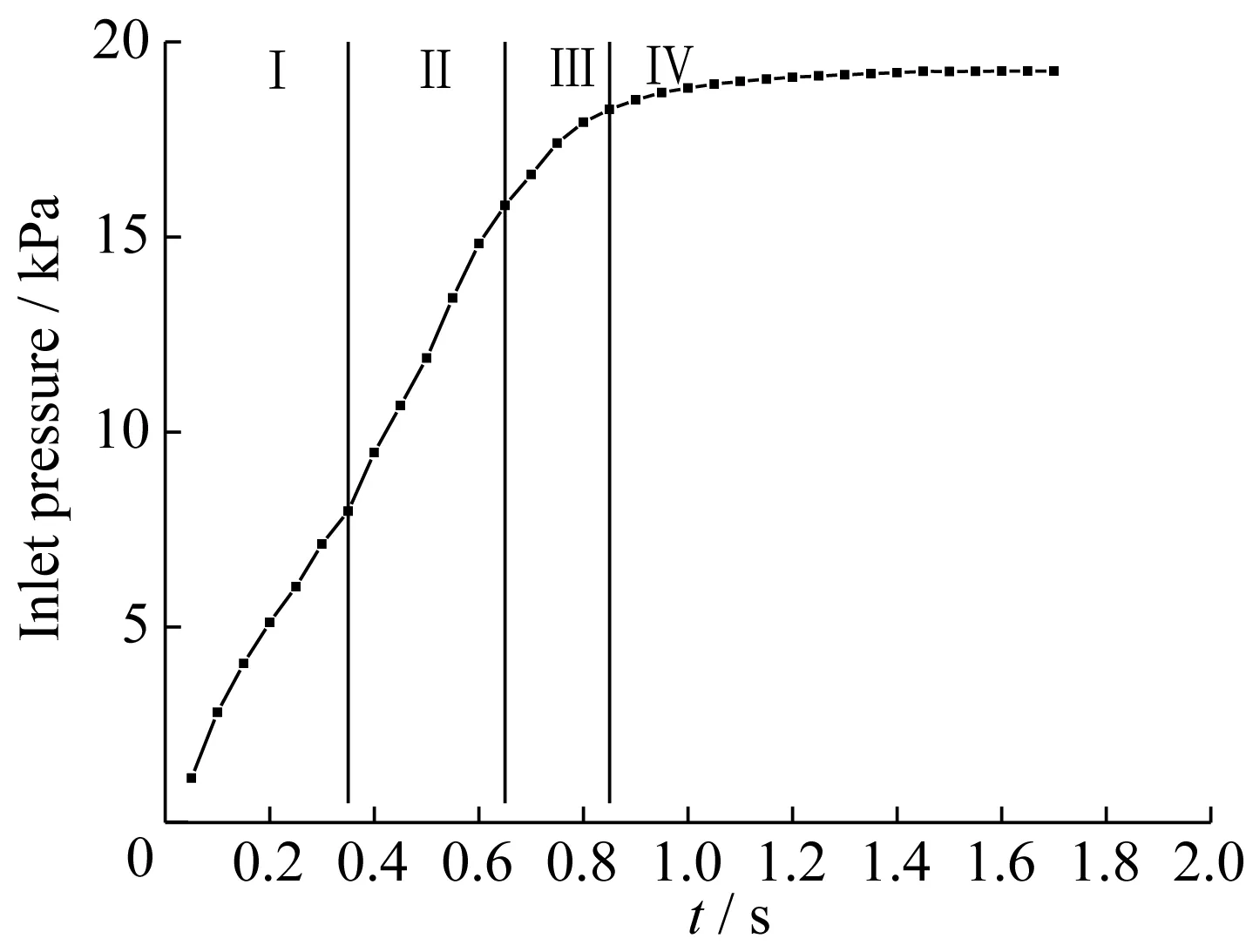
图7 入口压力随时间的变化(v=0.5 m/s)

经过计算发现,二维双尺度能较为真实地反映树脂在编织纤维内的浸渍情况,为下文计算所得结果的准确性提供了保证。

3 结果与讨论

3.1 参数设定

在研究纤维结构的影响时,假设单根纤维丝的半径为20 μm,纤维孔隙率为0.4,经过式(1)和式(3)计算,其纵向渗透率与横向渗透率分别为9.98×10-12m2和2.72×10-13m2,树脂黏度为0.06 Pa·s,注射压力为0.1 MPa,轴向孔隙宽度与横向孔隙宽度变化范围是0.1～0.9 mm,变化幅度为0.2 mm。在研究树脂性能影响时,在上述研究的基础上选出了最优化结构,进一步进行黏度在0.06～0.14 Pa·s范围内的比较。

3.2 轴向孔隙宽度

轴向孔隙宽度的大小主要影响树脂在大孔隙内的流动速度以及流量,进而影响树脂向纤维带的横向浸渍能力。当轴向孔隙宽度较小时,树脂在大孔隙内的流动速度较小,与纤维带内的树脂流动速度差距不大,这本有利于其横向浸渍,但由于轴向孔隙通道较窄造成其内部整体树脂流量小,横向浸渍量有限。因此,纤维带主要依靠流动方向上的树脂浸渍,而这部分主要以树脂对纤维的绕流为主,故整体浸渍时间长。

图8所示为树脂在0.1 MPa的压力驱动下,不同轴向宽度编织纤维浸渍速率与时间的关系。从图8中可以观察到浸渍速率的趋势是先快后慢,而且随着轴向孔隙宽度的增加,前期(树脂体积分数低于70%)浸渍时间不断减少。但是,当宽度超过0.5 mm之后,前期浸渍速率基本一致。经过分析,由于轴向孔隙通道的增大,流动阻力减小,树脂在大孔隙通道流动速度加快,而且流动量也迅速增加。与0.1 mm及0.3 mm孔隙宽度不同,孔隙宽度超过0.5 mm之后,树脂在大孔隙通道浸渍影响显著。如图9所示,树脂沿流动方向对纤维束的浸渍能力相差无几,但是大孔隙通道内树脂的浸渍情况却差别很大,与0.1 mm孔隙宽度相比,靠近入口的0.5 mm宽度轴向孔隙完全浸渍,并开始向孔隙流动以及两侧纤维带横向浸渍。如上所述,孔隙通道宽度增加,流动阻力相应减小,树脂能优先浸渍大孔隙通道,同时也能横向浸渍纤维带,所以前期浸渍时间能迅速减小,而且本次数值模拟得到的编织纤维内树脂流动情况与Gourichon[18]描述的一致,也符合前文预测结果。

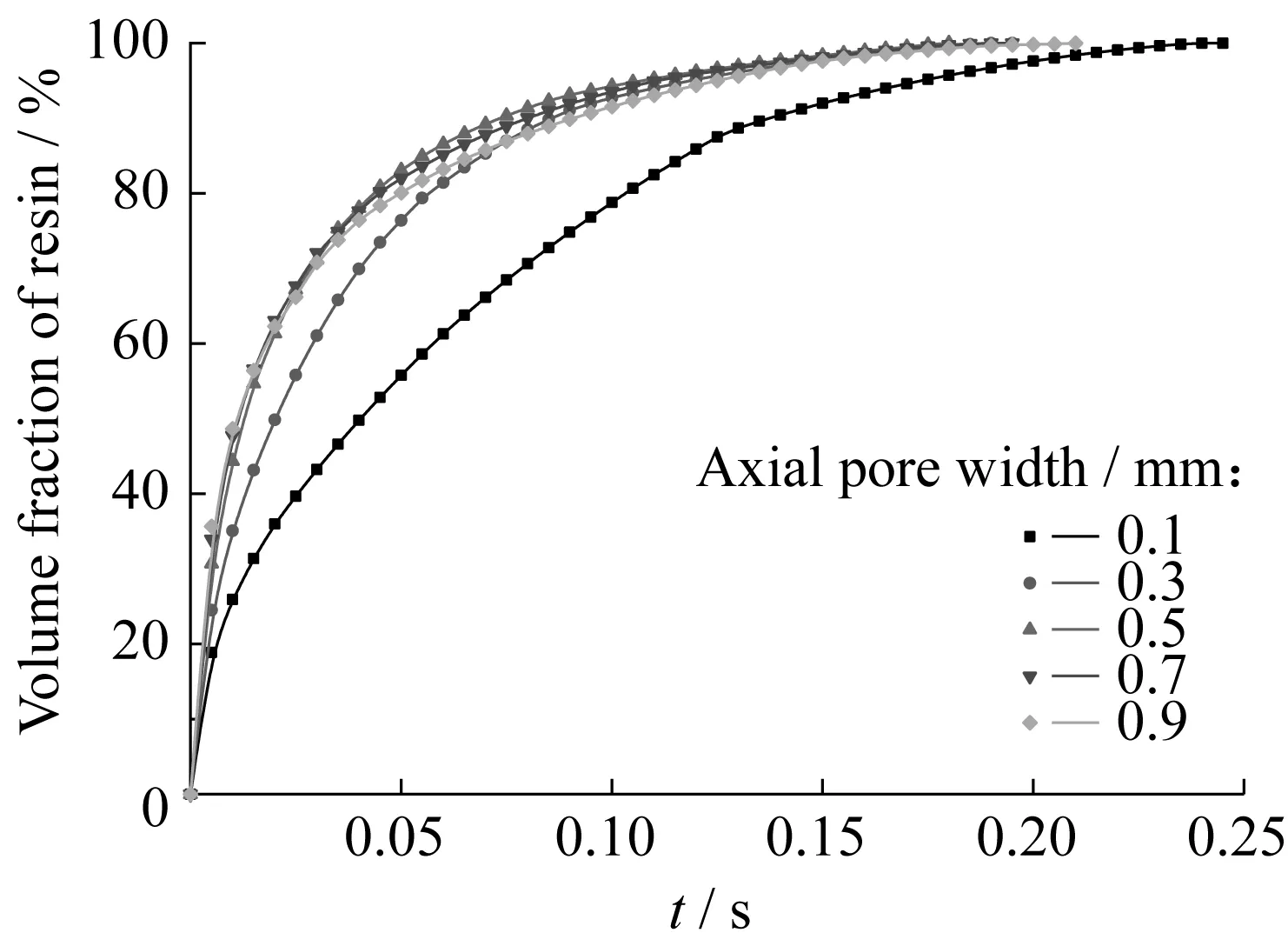
图8 不同轴向孔隙宽度编织纤维内的树脂浸渍过程

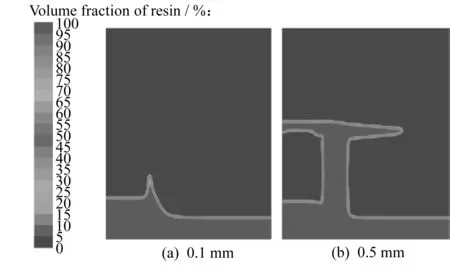
图9 不同轴向宽度编织纤维内的树脂浸渍对比(0.002 5 s)

从图8和图10可以看出,轴向孔隙宽度超过0.5 mm以后,完全浸渍的时间又随着宽度的增加而增加,增幅与前者降幅相比则较小。这主要由两个原因造成:一是轴向孔隙完全浸渍后,树脂沿轴向孔隙通道流出还是横向浸渍展开了竞争,由于宽度增加导致阻力减小,树脂沿轴向孔隙通道流出优势更为明显。从图11可以看出,随着轴向孔隙宽度的增加,其内部树脂流动速度与纤维束内树脂的浸渍速度差距越来越大,使得树脂主要沿轴向孔隙通道流动,故而相对减少了横向浸渍树脂量,进而影响浸渍时间;二是轴向孔隙通道宽度的增加,低黏度的流体在压差推动下容易流动不稳,而一旦流动不稳,流体分裂与融合的过程则较易形成小气泡。最终,这些轴向孔隙通道内形成的气泡会进入纤维束中,而树脂在纤维束内的整体运动速度较慢,小气泡不易排除,从而整体浸渍时间增加。

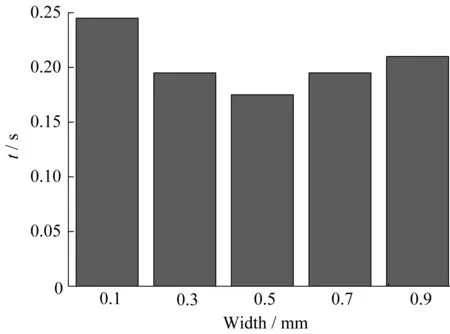
图10 不同轴向孔隙宽度编织纤维内的树脂浸渍总时间

图11 不同轴向孔隙宽度编织纤维内的树脂浸渍速度对比

3.3 横向孔隙宽度

轴向孔隙宽度主要决定前期树脂流动量以及树脂的横向浸渍程度,而横向宽度则影响横向通道内的树脂流动能力,进而影响树脂在下一排纤维束沿流动方向上的浸渍程度。

图12所示为0.001 5 s时不同横向宽度编织纤维内的树脂浸渍对比情况(浅色区域为树脂,深色区域为空气),从图中可以明显看到,当横向宽度为0.1 mm时,树脂在横向通道内流动阻力较大,甚至超过了纤维束内的渗透阻力,此时树脂以横向浸渍纤维束为主。随着横向通道宽度的增加,沿程阻力减小,树脂逐渐以横向通道流动为主,增加了与下一排纤维带的接触面积,使得树脂整体浸渍能力提高。

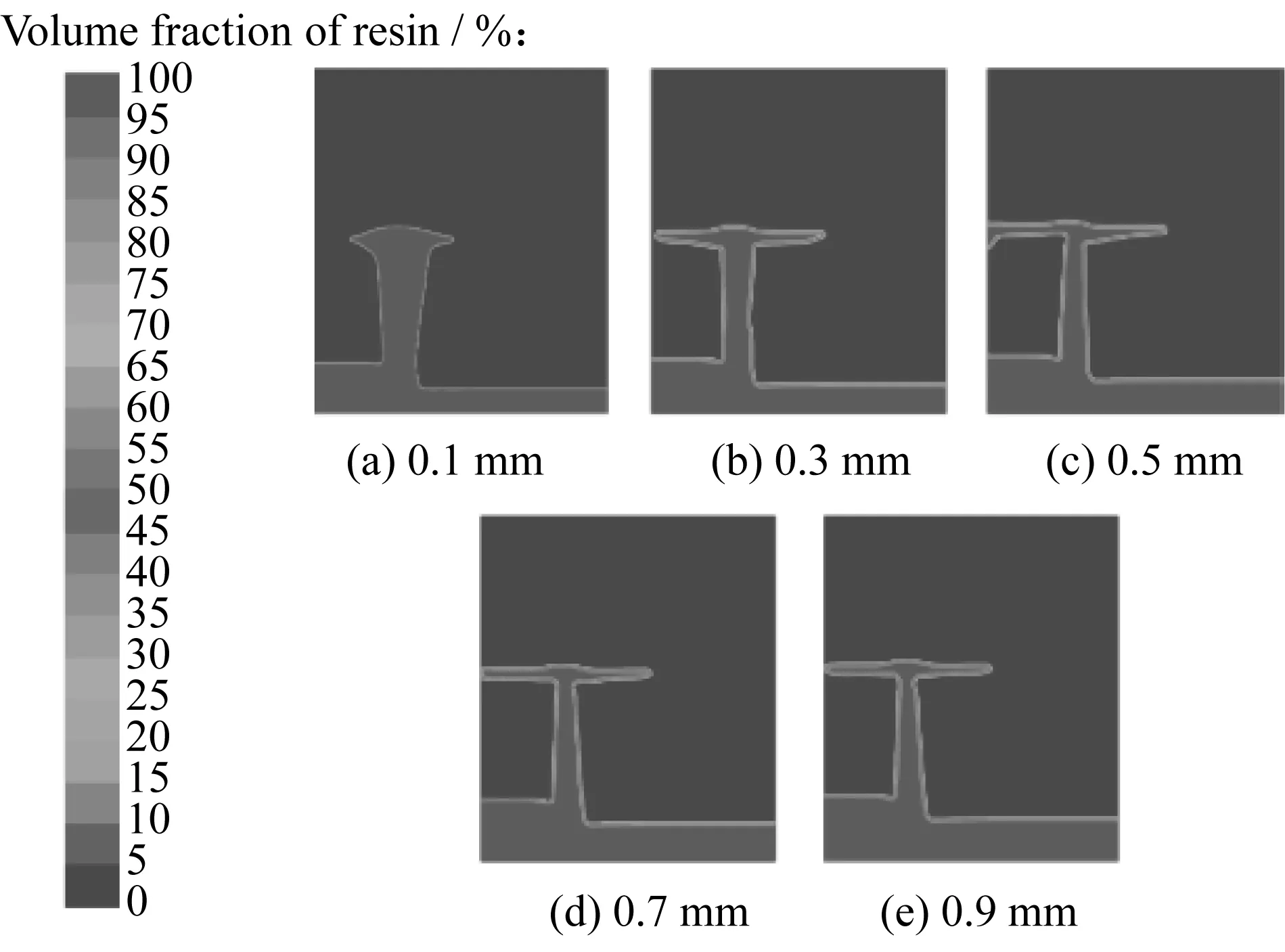
图12 不同横向孔隙宽度编织纤维内的树脂浸渍对比(0.001 5 s)

图13所示为不同横向宽度编织纤维内的树脂浸渍过程曲线。横向宽度超过(包含) 0.3 mm后,树脂的整个浸渍过程十分相近,不过浸渍量为75%～90%时,随着横向宽度的增加,曲线波动明显。这是因为在轴向宽度不变的情况下,横向宽度不断增加,沿轴向孔隙进入横向孔隙的树脂不足以填充整个横向孔隙通道,类似树脂突然进入突扩管的扩展段,受力发生改变,树脂流动也就变得不稳定,不像理想中那样树脂平推赶走大孔隙内的气泡,而是大孔隙内的气体裹挟在树脂内部,形成大小不一的气泡,如图14所示。这些气泡会有部分进入下一排纤维带中,由于气泡体积不均一,运动速度必然也不尽相同,这就造成随后的气体排出速度不一致,也就发生了图13中曲线波动的情况。图15所示为不同横向孔隙宽度编织纤维内的树脂浸渍总时间。上述情况同时也解释了图15中随着横向宽度的增加完全浸渍时间又开始增加的现象。因为一旦气体变成裹挟在树脂中的小气泡时,它的排出过程就比较复杂而缓慢,相应浸渍时间变长。一开始浸渍时间减少,原因如上所述,合适的横向宽度有利于树脂的流动,扩大浸渍的横截面积,从而达到加快浸渍过程的目的。

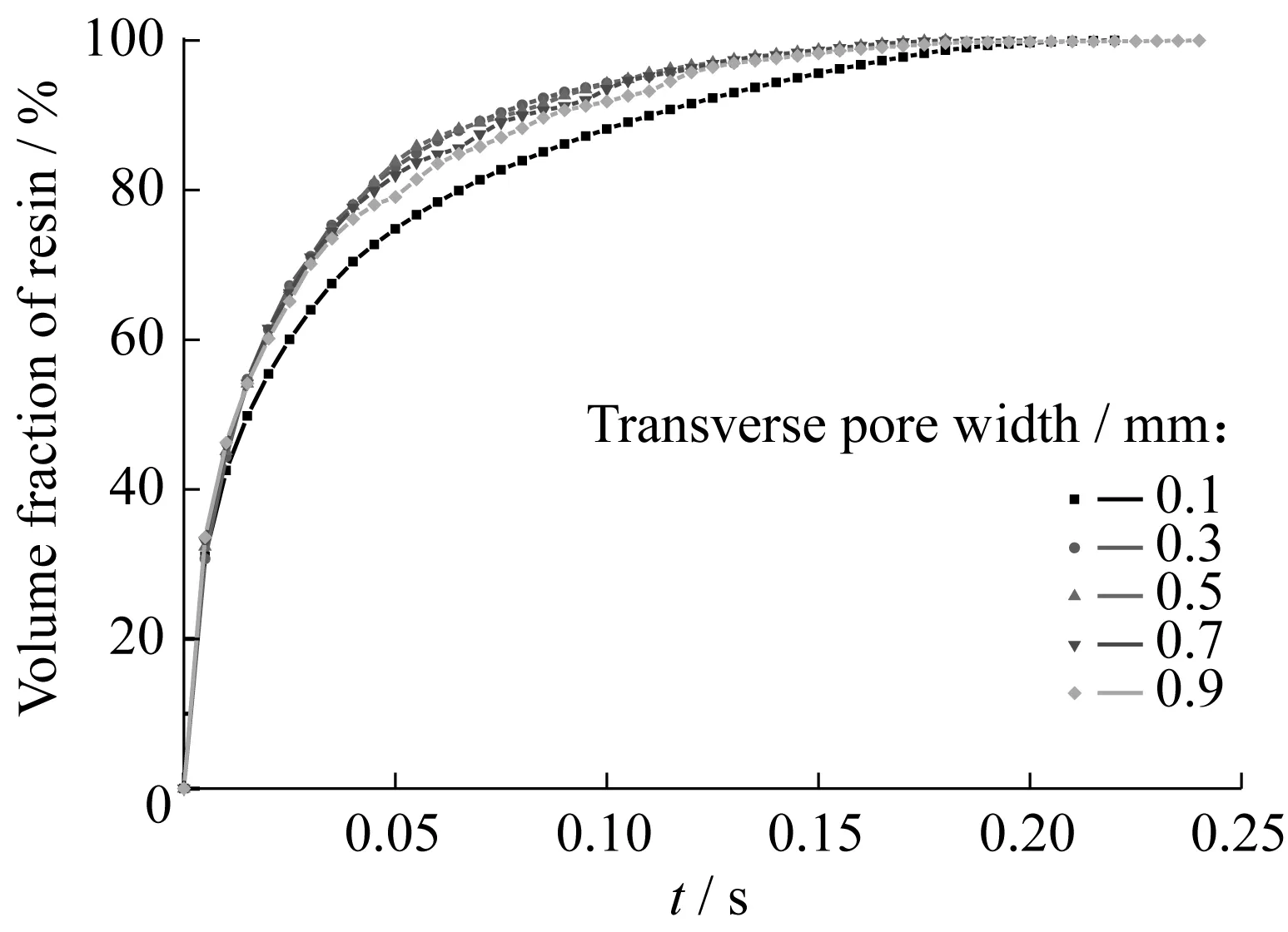
图13 不同横向孔隙宽度编织纤维内的树脂浸渍过程曲线

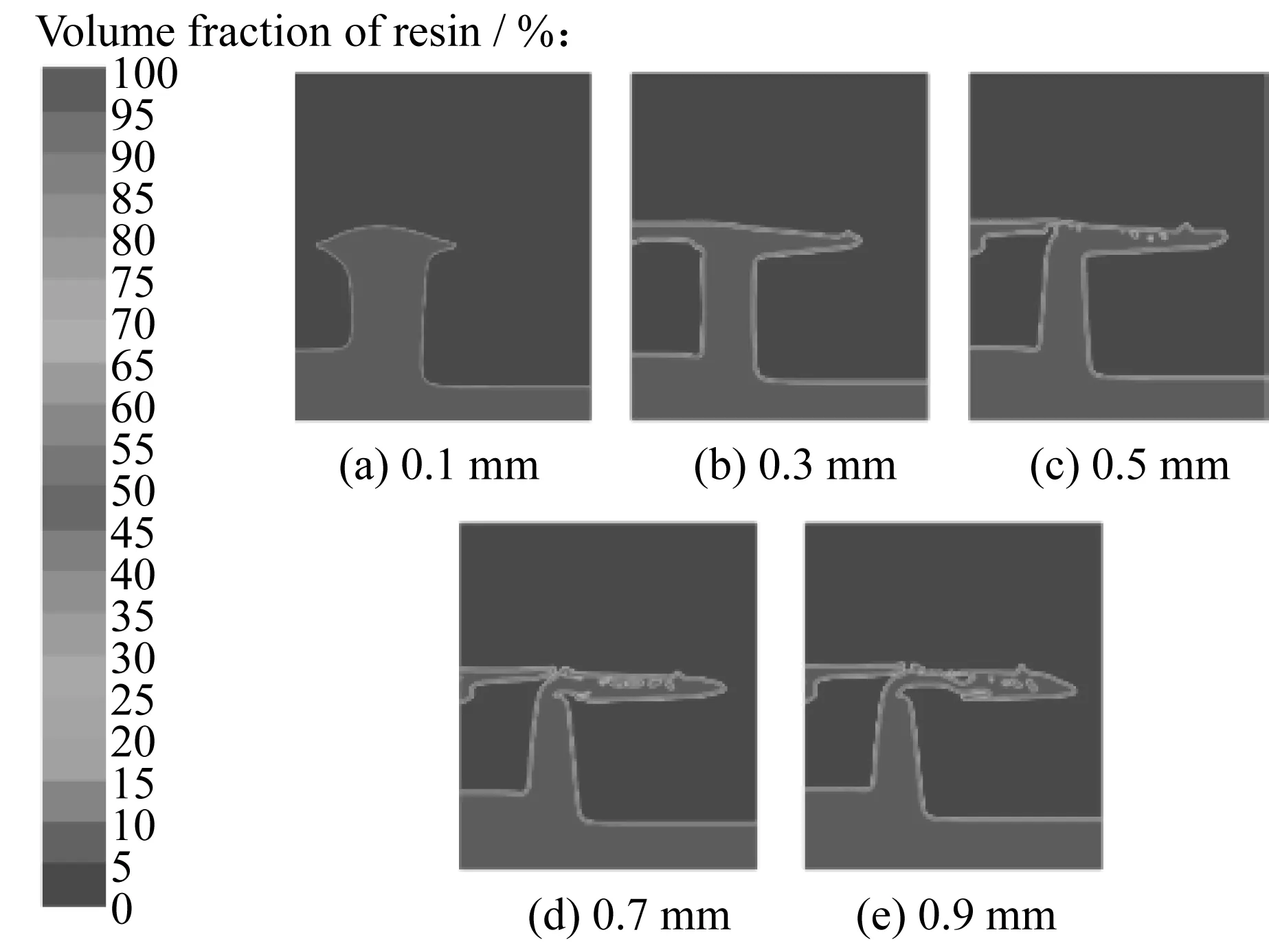
图14 不同横向孔隙宽度编织纤维内的气泡分布情况(0.003 s)

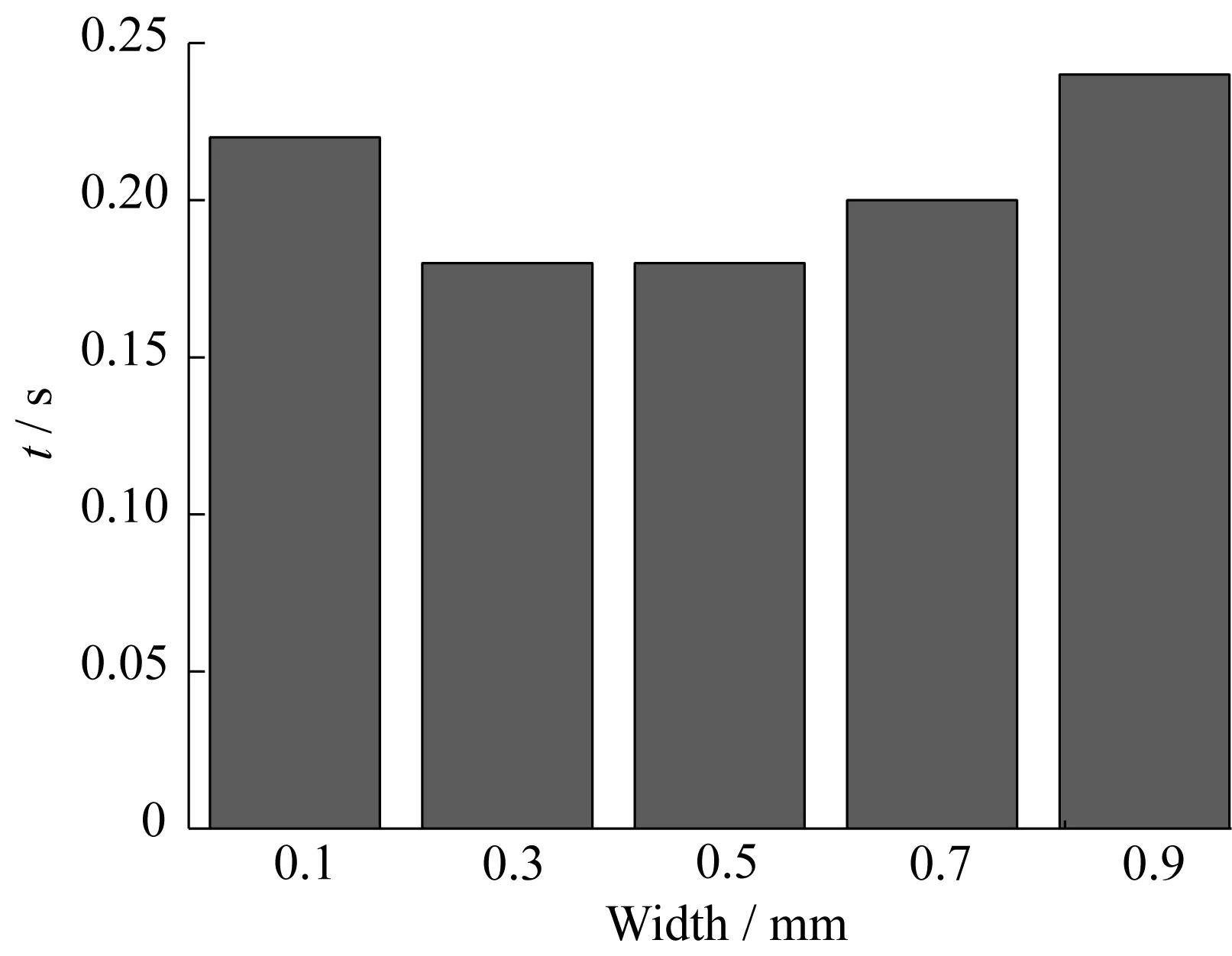
图15 不同横向孔隙宽度编织纤维内的树脂浸渍总时间

3.4 树脂黏度

树脂的黏度与体系的反应程度、温度、剪切力、剪切速率等多种因素有关,是一个复杂的变量。本文中假设为等温条件,改变树脂黏度，使之在0.06～0.14 Pa·s范围变化。

图16所示为不同黏度树脂在编织纤维内的浸渍过程曲线。从图中可以看出,不同黏度的浸渍趋势是相似的,都是前期快,后期比较缓慢。一部分原因可以根据压差动力dp/dx进行解释,在恒定压力条件下,前期树脂流动前沿dx较小,则压差动力大,树脂浸渍速度快,而后期随着树脂体积分数增加,前沿距离变大,压差动力渐渐减小,相应的浸渍速度降低,因此曲线斜率由大变小,最后趋于零。另一部分原因就是前期树脂浸渍以大孔隙通道为主,其内部阻力与纤维束内的渗透阻力相比几乎可以忽略,所以浸渍速度较快,根据图16中曲线的切线斜率比较,可知前期浸渍速度比后期平均大十几倍。

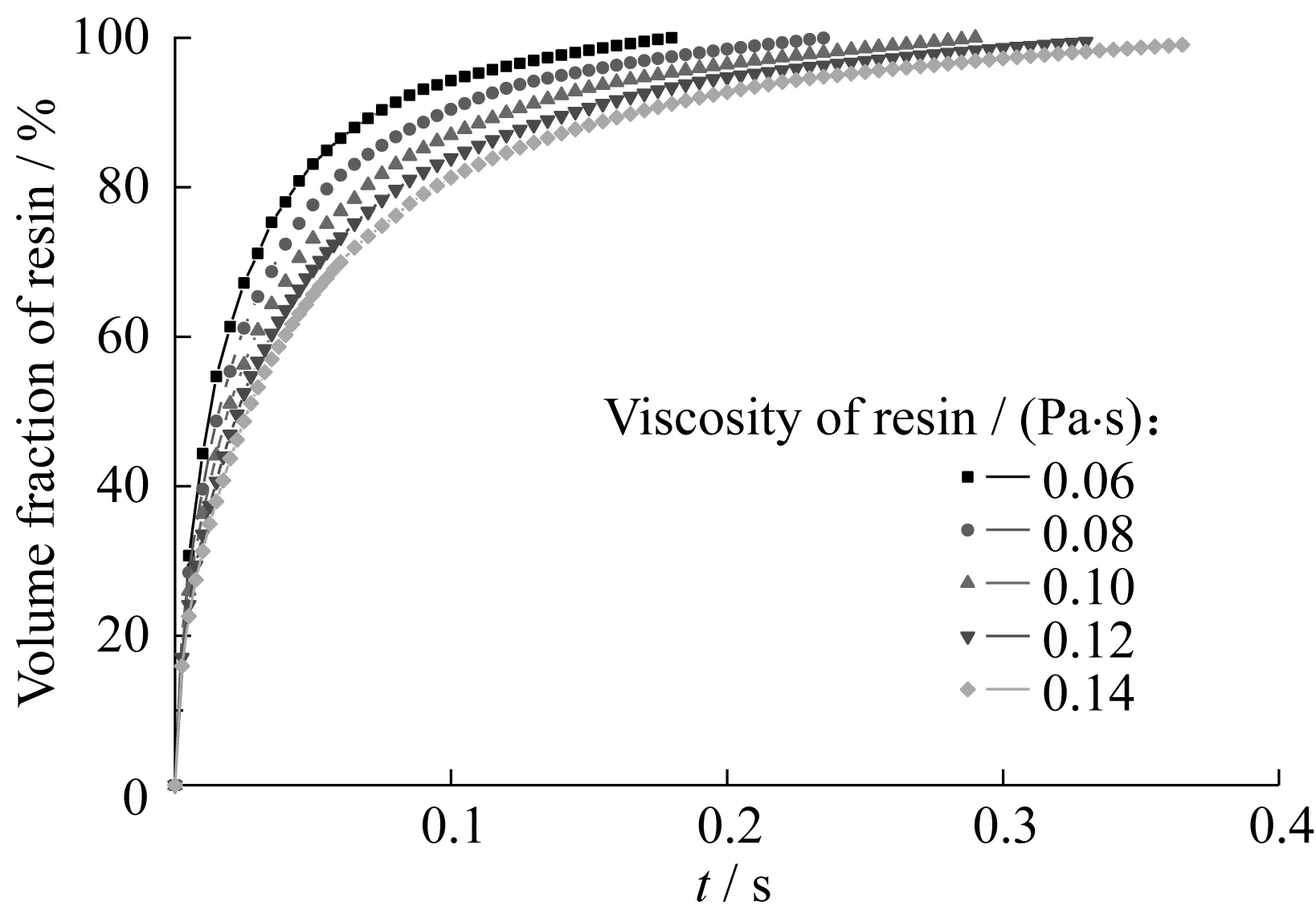
图16 不同黏度树脂在编织纤维内的浸渍过程曲线

随着树脂黏度的增加,浸渍总时间也在增加,趋势接近线性增加。在理想的一维浸渍条件下(均匀介质,各处渗透率相等),理论分析得到的流动前沿xf与时间t的关系[20]如下:

(14)

将式(14)变换后得到式(15):

(15)

上述结果表明,当浸渍距离一定时,浸渍时间与树脂黏度成正比。本文模拟得到的结果基本符合这一结论,只是与理想条件相比,本文存在大孔隙通道,而且纤维带轴向与横向渗透率不同,这两方面因素使得浸渍时间不完全与树脂黏度成正比,随着黏度的增加,浸渍时间的增加幅度越来越小。

4 结 论

本文提出二维双尺度模型,并对其进行了数值模拟,以编织结构变化对浸渍影响研究为主,数值模拟结果揭示了树脂在浸渍编织纤维时,纤维结构存在最佳尺寸。此外还研究了树脂黏度的增加对树脂流动的影响,着重观察气泡产生以及对其排除的过程,两者为预测充模时间以及气泡产生位置与其含量提供了重要的借鉴作用,所得结论如下:

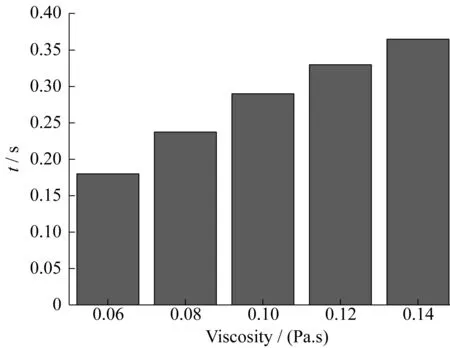
图17 不同粘度树脂在编织纤维内的浸渍总时间

(1) 当轴向孔隙宽度为0.5 mm时,树脂浸渍时间相比其他宽度的纤维结构要短,而且气泡在运动过程中分裂成小气泡的可能性最小,从而在整个浸渍过程中,能使充模时间与气含量达到最佳组合。

(2) 当横向孔隙宽度为0.3 mm与0.5 mm时,浸渍时间几乎相同,但是较窄的宽度能提高纤维的体积含量,进而提升最终制品的性能。此外,就横向宽度0.3 mm与0.5 mm相比较,孔隙通道的减小,也使制品内部气泡存在的几率降低。综合比较,横向孔隙宽度为0.3 mm时占优。

(3) 随着树脂黏度的增加,浸渍时间也在增加,但是增加的幅度不断减小。浸渍时间的增加主要与黏度增加后树脂内部的剪切应力增加有关,而与气泡分裂造成的排除困难关联度较少,因为黏度的增加,对气泡运动轨迹的变化影响较小。

符号说明：

A——横截面积

K——渗透率,m2

K⊥——横向渗透率,m2

K∥——轴向渗透率,m2

l——量纲为一的参数

p——压力,Pa

p0——注射压力,Pa

r——纤维半径,μm

r0——注射点半径,m

Sm——源项

t——时间,s

ut——树脂间流动速度,m/s

u——x方向速度,m/s

v——y方向速度,m/s

WA——轴向孔隙宽度,mm

WT——横向孔隙宽度,mm

xf——流动前沿,m

α——树脂相体积分数

ε——孔隙率

ρ——平均密度,kg/m3

ρa——空气密度,kg/m3

ρr——树脂密度,kg/m3

μ——平均黏度,Pa·s

μa——空气黏度,Pa·s

μr——树脂黏度,Pa·s

[1]GRÖSSING H,STADLMAJER N,FAUSTER E,etal.Flow front advancement during composite processing:Predictions from numerical filling simulation tools in comparison with real-world experiments[J].Polymer Composites,2015,39(9)：2782-2793.

[2]SAAD A,ECHCHELH A,HATTABI M,etal.Optimization of the cycle time in resin transfer molding process by numerical simulation[J].Journal of Reinforced Plastics and Composites,2012,31(20):1388-1399.

[3]JUDD N C.Voids and their effects on the mechanical properties of composites:An appraisal[J].Sampe Journal,1978,14(1):55-62.

[4]MIDDELBERG J M,BARBER T J,LEONG S S,etal.Computational fluid dynamics analysis of the acoustic performance of various simple expansion chamber mufflers[C]//Proceedings of Acoustics.Australia:Australian Acoustical Society,2004:123-127.

[5]GOU J,ZHANG C,LIANG Z,etal.Resin transfer molding process optimization using numerical simulation and design of experiments approach[J].Polymer Composites,2003,24(1):1-12.

[6]PARK C H,WOO L.Modeling void formation and unsaturated flow in liquid composite molding processes:A survey and review[J].Journal of Reinforced Plastics and Composites,2011,30(11):957-977.

[7]YANG J,JIA Y,SUN S,etal.Mesoscopic simulation of the impregnating process of unidirectional fibrous preform in resin transfer molding[J].Materials Science and Engineering:A,2006,435/436:515-520.

[8]PADAKI N V,ALAGIRUSAMY R,DEOPURA B,etal.Studies on preform properties of multilayer interlocked woven structures using fabric geometrical factors[J].Journal of Industrial Textiles,2010,39(4):327-346.

[9]CHEN Y F,STELSON K,VOLLERT V.Prediction of filling time and vent locations for resin transfer molds[J].Journal of Composite Materials,1997,31(11):1141-1161.

[10]GOKCE A,ADVANI S G.Simultaneous gate and vent location optimization in liquid composite molding processes[J].Composites:Part A.Applied Science and Manufacturing,2004,35(12):1419-1432.

[12]秦伟,李海晨，张志谦，等.RTM工艺树脂流动过程数值模拟及实验比较[J].复合材料学报,2003,20(4):77-80.

[13]PORTO J D S,LETZOW M,SANTOS E D D,etal.Computational modeling of rtm and lrtm processes applied to complex geometries[J].Journal of the Brazilian Society of Mechanical Sciences & Engineering,2012,11(1):93-99.

[14]BRUSCHKE M,ADVANI S.Flow of generalized newtonian fluids across a periodic array of cylinders[J].Journal of Rheology,1993,37(3):479-498.

[15]SCHELL J,SIEGRIST M,ERMANNI P.Experimental determination of the transversal and longitudinal fibre bundle permeability[J].Applied Composite Materials,2007,14(2):117-128.

[16]TAN H,PILLAI K M.Multiscale modeling of unsaturated flow in dual-scale fiber preforms of liquid composite molding I:Isothermal flows[J].Composites:Part A.Applied Science and Manufacturing,2012,43(1):1-13.

[17]ISOLDI L A,OLIVEIRA C P,ROCHA L A,etal.Three-dimensional numerical modeling of RTM and LRTM processes[J].Journal of the Brazilian Society of Mechanical Sciences and Engineering,2012,34(2):105-111.

[18]GOURICHON B,BINETRUY C,KRAWCZAK P.Experimental investigation of high fiber tow count fabric unsaturation during RTM[J].Composites Science and Technology,2006,66(7):976-982.

[19]PARNAS R S,HOWARD J G,LUCE T L,etal.Permeability characterization:Part 1.A proposed standard reference fabric for permeability[J].Polymer Composites,1995,16(6):429-445.

[20]MASOODI R,PILLAI K M,GRAHL N,etal.Numerical simulation of LCM mold-filling during the manufacture of natural fiber composites[J].Journal of Reinforced Plastics and Composites,2012,31(6):363-378.

Numerical Simulation of the Influence of Fibrous Structure on Resin Filling in RTM Process

ZHOU Yun-fei, FANG Xun, WANG Wen-qi, GUO Wei-hong, DAI Gan-ce

(State Key Laboratory of Chemical Engineering,East China University of Science and Technology,Shanghai 200237,China)

Reducing mold filling time and bubble content are the two key issues in Resin Transfer Molding (RTM).The two-phase flow model was built in this paper based on Newtonian fluid and Navier-Stokes equations.Combining the FVM with volume of fluid approach,a successful numerical simulation of isothermal filling stage was achieved.The changes of physical parameters in the filling stage,the influence of the fibrous structure and viscosity of the resin on mold filling time and the formation and exclusion of voids were analyzed.Moreover,there is a good agreement between numerical results and the analytical solutions as well as experimental results.The numerical results show that the model can accurately reflect the process of resin filling.For low viscous melt,pore width of woven fiber has the best horizontal and vertical size.In addition,increase of the viscosity of resin will affect the formation and the removal process of air bubbles in the fiber,thus influence the final mold filling time.

mold filling time; numerical simulation; FVM; VOF; fibrous structure

1006-3080(2017)02-0162-09

10.14135/j.cnki.1006-3080.2017.02.003

2016-07-11

周云飞(1991-),男,浙江余姚人,硕士生,研究方向为复合材料加工成型及其数值模拟。E-mail:yyzhouyunfei@163.com

郭卫红,E-mail:guoweihong@ecust.edu.cn

TB332

A