自吸泵自吸过程气液两相流数值模拟分析

刘洪生, 苏永升(华东理工大学承压系统与安全教育部重点实验室,上海 200237)

自吸泵自吸过程气液两相流数值模拟分析

刘洪生, 苏永升
(华东理工大学承压系统与安全教育部重点实验室,上海 200237)

自吸泵的自吸过程是一个很复杂的气液两相混合流动与分离过程。本文利用非稳态数值模拟方法模拟自吸泵自吸过程,初始条件为进水管及出水管含有部分空气,然后估算自吸时间。模拟结果表明:泵吸气和排气主要集中在自吸初期,期间叶轮入口和泵出口气含率最高分别可达62.4%和45.3%;叶轮入口气含率变化较泵出口气含率变化剧烈;此外,叶轮与导叶间隙对自吸性能有影响,间隙与自吸时间呈负相关变化,说明较大的间隙有利于泵的自吸。

自吸泵; 自吸过程; 气液两相流; 非稳态数值模拟

自吸泵是一种特殊用途的离心泵,利用泵的特殊结构及气液混合原理实现抽吸气体,目前广泛应用在农业排灌、城市消防以及石化等工业领域[1]。自吸泵具有如下特点:能够自动排出吸入管路及泵体内的空气；在第一次启动前和灌泵后,如吸入管路不漏气,那么在以后泵启动时则无需灌泵[2]。

随着计算流体力学的快速发展,近年来一些学者对自吸泵进行了实验与数值模拟研究。李红等[3]对自吸泵在自吸过程中的内部流场进行了非定常模拟,分析得出了自吸泵自吸过程中内部气液两相流动的特点;王洋等[4]研究了不同工况下漩涡自吸泵内部瞬态流动特性,得到了泵内部流动情况和监测点处压力脉动特性。崔玉松等[5]针对自吸泵的气液分离室对泵性能影响很大的问题,选择不同分离室高度进行性能预测,最后得出在小流量区时气液分离室高度对泵效率影响很小;John Kanute[6]分析了蜗壳式自吸与扩压式自吸的原理,并分析了两种不同自吸方式的优缺点。范宗霖[7]对外混式自吸泵的自吸时间和自吸高度的计算方法进行了讨论,给出了不同自吸高度下自吸时间的计算公式。陈茂庆等[8]研究了回流孔对自吸泵自吸性能的影响,最后给出临界回流孔与自吸时间的关系。

自吸泵自吸过程很复杂,关于自吸的部分还没有比较完善的设计方法,目前对自吸泵的数值模拟主要集中在两方面:一是自吸泵正常输水运转时内部流场信息,比如模拟工况改变时泵水力性能变化;二是模拟不同进口气含率时泵内部流动情况[9],对带导叶的自吸泵自吸时间的非稳态数值模拟鲜见报道。本文选取一台立式导叶自吸泵,利用ANSYS CFX软件对自吸泵自吸过程中气液两相进行非稳态流数值模拟分析。同时,依据导叶基圆直径与叶轮外径之间相关公式[10],进一步探讨了改变叶轮与导叶之间间隙对自吸时间的影响。

1 研究对象及网格划分

1.1 计算模型

选取一台比转速为58的立式导叶自吸泵作为研究对象,该泵的主要过流部件包括叶轮、导叶、储水室、气液分离室等。泵的设计流量为13.5 m3/h,额定转速为2 970 r/min,扬程为25 m;泵的主要结构参数如表1所示,叶轮叶片数为6,泵的流道造型如图1所示。利用Solid-works软件对自吸泵的过流部件进行三维建模,数值模拟计算区域由进出口管、储水室、导叶、叶轮和气液分离室5部分组成。

表1 自吸泵设计参数

泵采用离心式叶轮,导叶采用径向设计方法,叶片数为7,进口直径为149 mm,其余设计参数如表2所示。

图1 自吸泵流道

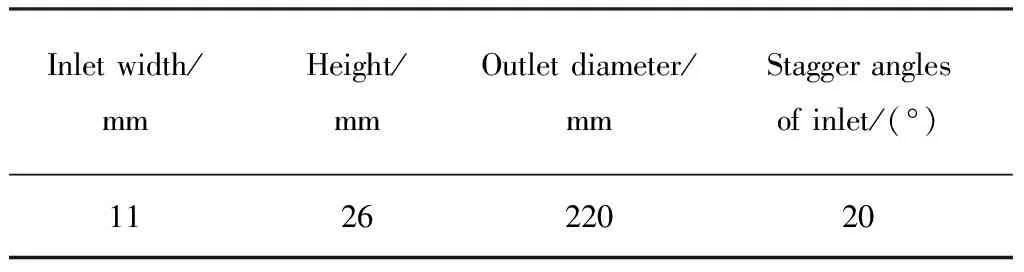
Inletwidth/mmHeight/mmOutletdiameter/mmStaggeranglesofinlet/(°)112622020

1.2 网格划分

由于自吸泵叶轮和导叶形状复杂,特别是形状扭曲的叶片与导叶造成计算域的复杂,因此应用四面体非结构网格对流道进行划分。整机流道网格如图2所示。

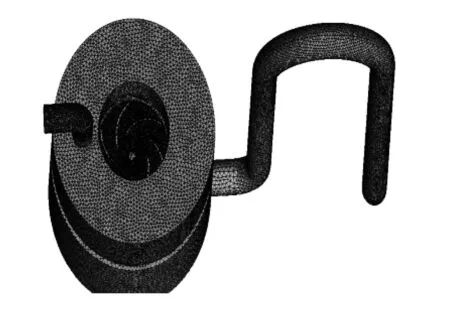
图2 自吸泵数值计算网格

1.3 网格无关性验证

网格无关性验证的目的是为了保证自吸泵的外特性及主要性能参数不受网格数目影响,在设计流量下计算比较不同网格数目对应的扬程与效率以此进行网格无关性验证。本文选取了4组不同的网格数目,同时保证进出口边界条件也一样,在设计流量下经过稳态计算所得自吸泵性能参数如表3所示。

从表3可以看出,随着网格数目的增大,扬程(H)和效率(η)基本趋于恒定,变化范围很小,表明数值计算结果受网格数目影响较小。综合考虑计算精度与计算时间,本文选择1.5×106左右的网格数目进行数值模拟计算,即方案2。

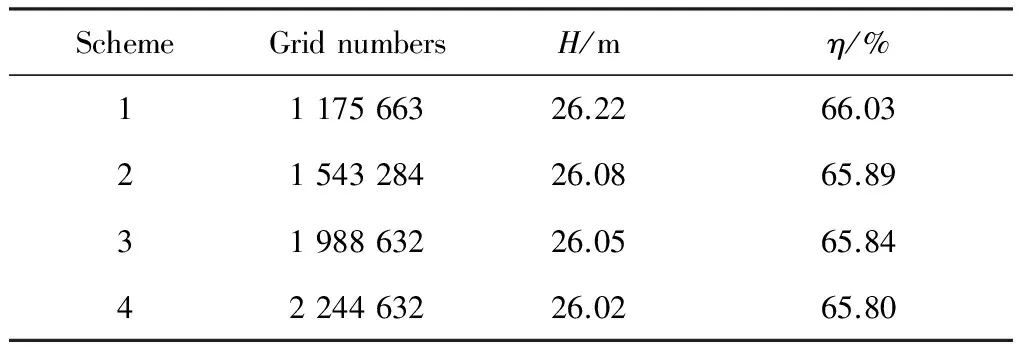
表3 网格无关性验证

2 数值计算方法

2.1 两相流控制方程

VOF模型的基本方程式由连续性方程、物性方程、混合流体的雷诺平均Navies-Stokes方程、湍动能方程(k方程)和湍动能率耗散方程(ε方程)5类方程组成[9]。根据不可压缩流体物性方程等可以得到各相体积组成的输运方程为

(1)

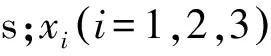
混合流体的雷诺平均Navier-Stokes方程为

(2)

(3)

式中:ui,uj为混合流体速度,m/s;μ1,μ2分别为第1相和第2相黏度系数,Pa·s;μ为混合流体黏度系数,Pa·s;μt为湍动能黏度系数,Pa·s;ρ为混合流体密度,kg/m3;φ1,φ2为各相体积分数;g为重力加速度,9.8 m/s2;xi(i=1,2,3)为直角坐标系中3个方向。

2.2 边界条件及初始条件

实际工作中叶轮从静止到恒定转速需要一定时间,但为了避免计算过于复杂,本文作以下假设:

(1) 泵的转速为定值,忽略泵启动过程中的转速变化。

(2) 气相与液相之间无热量交换,系统保持恒温。

(3) 当绝大部分气体排出时,便认为自吸过程完成。

选取25 ℃时的空气和水分别作为气相和液相,取进水管口为计算进口,出水管口为计算出口,进口以质量流量计,出口按opening(环境压力为大气压)设置,控制方程采用VOF方法和标准k-ε湍流模型;根据自吸泵的转速,时间步长设置为3.367×10-3s,内迭代的迭代次数上限取默认值20,固壁处采用绝热、无滑移边界条件。计算前对模型进行初始化,吸入管路以及出水管有一段空气,吸入管空气段长度为2 m,其余部分为水。

3 计算结果与分析

3.1 气液两相情况

图3选取了自吸过程中心截面上具有代表性4个时刻的气液两相分布图,其中α代表气含率,α=1表示全部为气相,α=0表示全部为液相。由图3(a)可以看出泵还未启动时,进水管及出水管的一部分含有空气,其余部分为水的情形;图3(b)显示当t=3.5 s时,随着叶轮旋转,管路中的气体进入泵内,此时气体已经进入气液分离室进行气液混合并分离,密度较小的气体经分离后通过出口管排出,随着自吸过程的进行,储水室中的气体越来越少;图3(c)显示大部分气体已经通过储水室进入气液分离室;图3(d)显示绝大部分气体已经排出,自吸过程基本完成,此时水泵进入正常工作状态。

图3 泵内中心截面气液两相分布

3.2 叶轮与导叶中的流动状态

为了判断在自吸过程中叶轮与导叶中流动情况,取2个典型时刻进行判断,如图4所示。图4(a)为泵自吸过程中大量吸入气体时叶轮与导叶的流线图,可以看出,此时叶轮与导叶流道中有很多漩涡,流线很不规则,这是由于泵的自吸过程是很复杂的气液两相混合与分离过程。图4(b)为气体基本排完时叶轮与导叶流道中的流线图,可以看出此时流道内已无漩涡,流线分布较规则。

图4 叶轮与导叶流线图

图5示出了由后处理得到的泵自吸过程中叶轮入口与泵出口气相流量随时间变化曲线。由图可知,泵大量吸入气体以及排出气体主要集中在自吸初期阶段。

图5 叶轮入口和泵出口处气相流量随时间变化情况

图6示出了自吸泵自吸过程中叶轮入口与泵出口气含率变化曲线。可以看出,开始时出水管有部分空气,在排气的初始时刻,出口气含率为1。从图中曲线可以看出,在自吸初期,叶轮入口气含率很高且变化剧烈,最高可达62.4%,之后迅速下降,在8.5 s之后,保持在5%上下波动;泵出口气含率最高可达45.3%,出口含气率曲线随时间变化相对平缓,在10 s之后基本维持在5%上下波动。自吸过程中泵出口气含率较叶轮入口气含率曲线变化平缓,这是由于管道中的气体刚进入储液室的流量比较大,未能与水混合均匀即进入叶轮,而泵出口的气体已经在气液分离室内经过混合与分离,故导致叶轮入口气含率较泵出口气含率变化剧烈;此外,泵出口气含率的峰值较叶轮进口气含率峰值有一个延迟,随着自吸泵自吸过程的进行,两者气含率逐渐趋于一致。

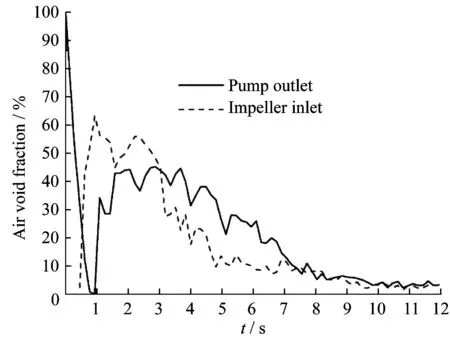
图6 叶轮入口和泵出口处气含率随时间变化情况

3.3 估算自吸时间

假定在整个自吸过程中没有相变发生,则理论上泵的自吸时间应等于吸入管中所有气体排出泵的时间。但由于气体经过叶轮进入气液分离室之后,与水已经混合较均匀,所以完全排出需较长时间,同时考虑到模拟计算会耗费较长时间,因此本文利用积分来估算自吸时间。

初始时进水管所含气体体积为0.003 91 m3,气体密度为1.185 kg/m3,可算出初始时气体质量为4.633 g。

根据图5作出12 s内泵出口气体质量对时间的累加值曲线L,如图7所示,可以看出,在8 s之后,L近似为一条直线,因此可作出L在8 s之后的趋势线(虚线所示)近似反映L的趋势,延长线与吸入管内初始气体质量的交点的横坐标为自吸时间。据此得到本文自吸时间为14.37 s,实际工作时的自吸时间可能会存在差异,但在分析判断自吸泵自吸时间时可采用此方法。

4 叶轮与导叶间隙对自吸时间的影响

叶轮与导叶间隙δ对自吸泵自吸时间有影响,根据文献[11]知δ一般取1～5 mm,δ不能太小,如果δ过小,一方面容易引起泵的噪声和振动,另一方面也会使安装困难、容易损坏;但间隙过大也会使泵正常工作时内泄漏增大,对泵的运行效率有影响。本文中叶轮与导叶间隙δ=2.0 mm。现改变叶轮与导叶间隙,制定两组方案,分别为δ=2.5 mm与δ=1.5 mm,利用同样的网格划分标准与数值模拟方法进行模拟,为便于对比,初始时吸水管内空气段长度相同,进出口边界条件设置也一样。图8示出了3组不同间隙时泵出口气含率对比情况。从图中可以看出,泵出口气含率曲线变化趋势基本一致,并且随着间隙的变大,气含率的峰值所对应的时间变短,这说明叶轮与导叶间隙变大后,自吸能力变大。

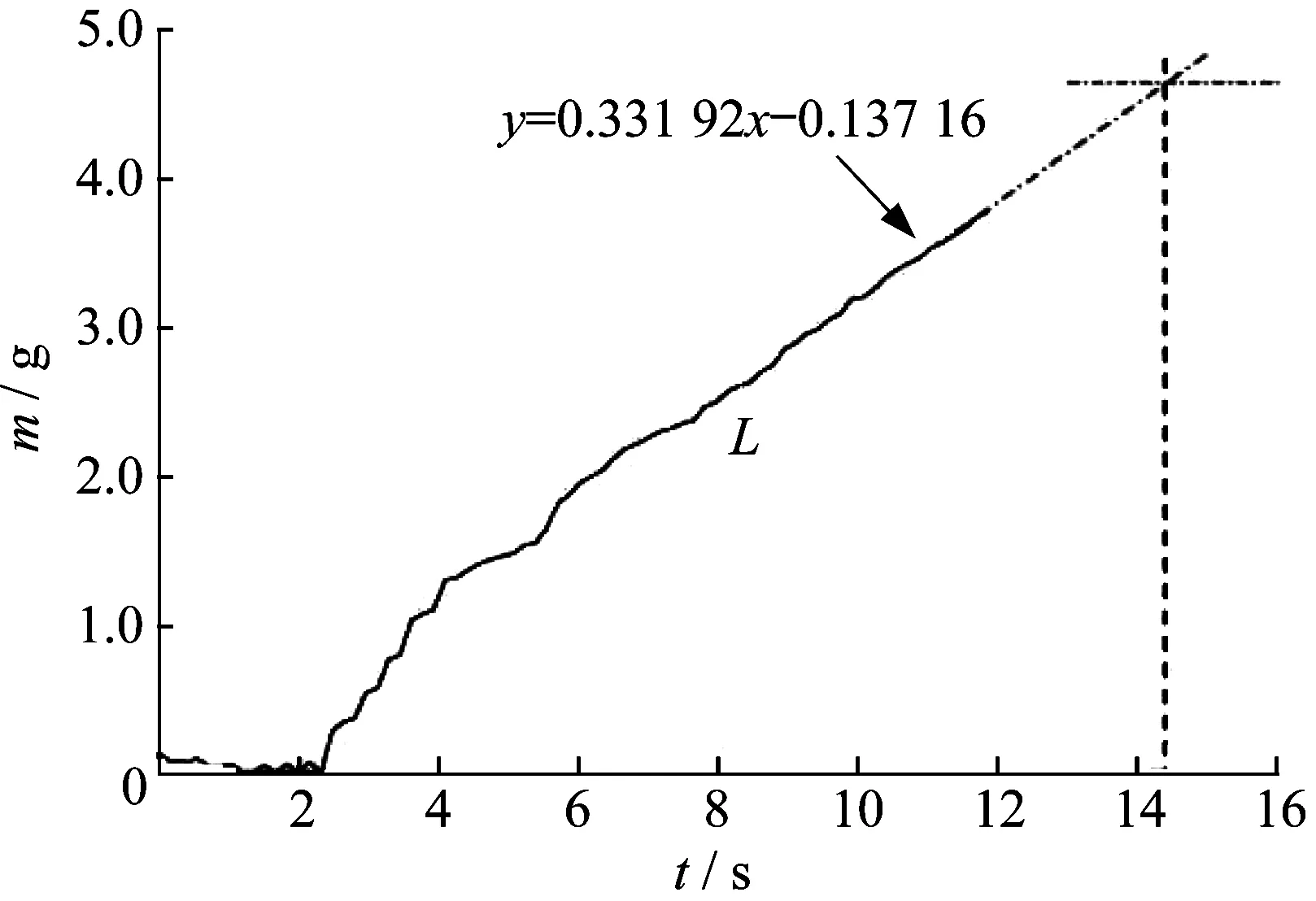
图7 泵出口气体质量对时间累加值

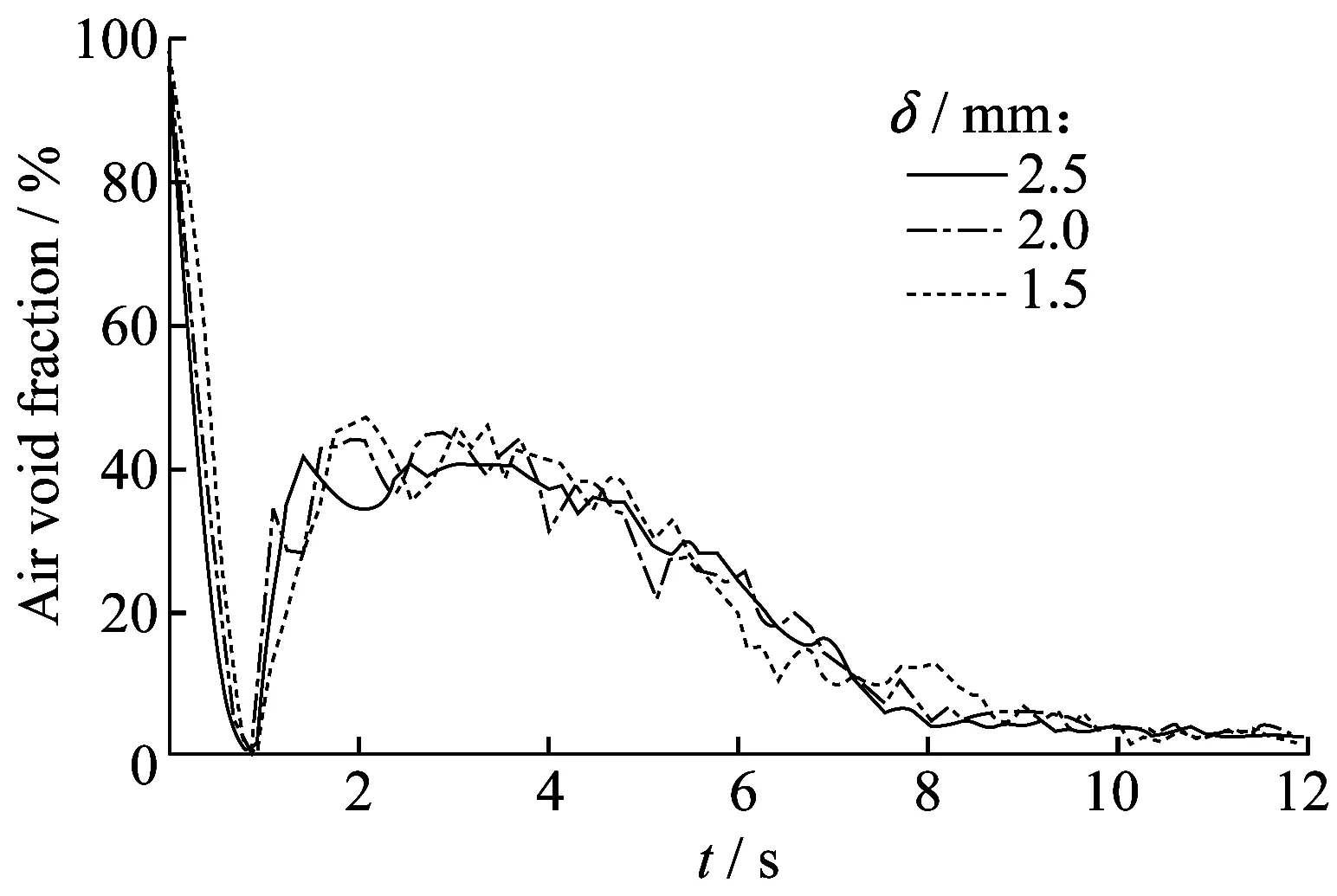
图8 不同间隙时泵出口气含率对比

图9所示为改变间隙后自吸时间的估算,利用与3.3节同样的方法即可求出自吸时间。表4示出了不同间隙时自吸时间对比,从表中可以看出随着间隙变大,自吸时间越来越小。

图10对比了叶轮与导叶不同间隙时泵出口气体质量与自吸时间关系。从图10可以看出,曲线变化趋势基本一致,间隙变小后,自吸时间变长;间隙变大后,自吸时间变短。此结果说明叶轮与导叶间隙对自吸的完成有影响,这是由于间隙变小后,经过气液分离之后的液体回流阻力变大,所以会使自吸时间变长。而较大的间隙有利于分离之后的液体回流和自吸时间减小;但间隙过大时也会使泵在正常工作时内泄漏增大,从而影响泵的运行效率。

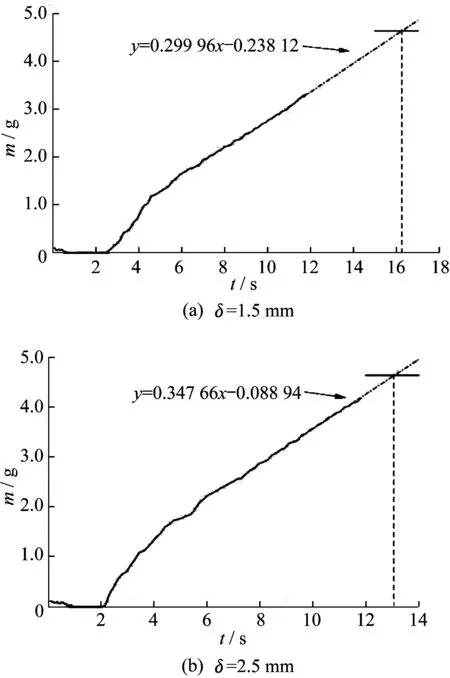
图9 不同间隙时自吸时间估算

δ/mmSelf⁃primingtime/s1．516．252．014．372．513．07

图10 不同间隙时泵出口气体质量与自吸时间关系对比

5 结 论

(1) 以进水管及出水管含有一段空气作为初始条件,模拟得到自吸过程中气液两相流场情况,通过计算得到叶轮入口与泵出口气相流量随时间变化关系以及叶轮进口与泵出口气含率随时间变化关系,由此估算自吸时间。

(2) 在自吸过程中,叶轮与导叶中的气液流动很复杂,流道中有很多漩涡,流线分布很不均匀;当气体基本排完时,流道中流线分布比较均匀。

(3) 当泵在自吸时,吸入和排气主要集中在自吸初期,此时叶轮入口气含率最高可达62.4%,泵出口气含率最高可达45.3%。之后叶轮入口气含率迅速下降,在8.5 s之后,保持在5%上下波动;泵出口气含率随时间变化相对平缓;泵出口气含率峰值较叶轮进口气含率峰值有一个延迟。

(4) 叶轮与导叶间隙对泵的自吸性能有影响。计算结果表明:当间隙变小后,自吸时间变长,这是因为间隙变小后,气液分离之后的液体回流阻力也会变大;当间隙变大后,自吸时间变短,说明间隙变大有利于泵的自吸性能,但过大的间隙也会使泵正常工作时内泄漏风险增大,影响泵的运行效率。

[1]郭晓梅,杨敏官,王春林.自吸泵现状分析[J].水泵技术,2002(1):27-29.

[2]赵雪华,朱天霞.泵的理论与应用[M].上海:华东理工大学出版社,1994.

[3]李红,徐德怀,李磊,等.自吸泵自吸过程瞬态流动的数值模拟[J].排灌机械工程学报,2013,31(7):565-569.

[4]王洋,彭帅,刘瑞华,等.漩涡自吸泵内部流场压力脉动数值模拟[J].排灌机械工程学报,2015,33(7):583-588.

[5]崔玉松,司艳雷,易同祥,等.漩涡自吸泵气液分离室结构对性能影响预测[J].排灌机械工程学报,2009，27(2):119-123.

[6]KANUTE J.Self-priming centrifugal pumps:A primer[J].World Pumps,2004(456):30-32.

[7]范宗霖.自吸泵的自吸时问及自吸高度计算[J].甘肃工业大学学报,1991，17(1):7-13.

[8]陈茂庆,吴卫东.回流孔对自吸离心泵自吸性能影响的研究[J].水泵技术,1998(1):26-30.

[9]李红,徐德怀,涂琴,等.自吸泵启动过程气液两相流动的数值模拟[J].农业工程学报,2013,29(3):77-83.

[10]关醒凡.现代泵理论与设计[M].北京:中国宇航出版社,2011.

[11]江帆,黄鹏.FLUENT高级应用与实例分析[M].北京:清华大学出版社,2008.

Numerical Simulation of Gas-Liquid Two-Phase Flow in Self-priming Pump During Self-priming Period

LIU Hong-sheng, SU Yong-sheng

(Key Laboratory of Pressurized Systems and Safety,Ministry of Education, East China University of Science and Technology,Shanghai 200237,China)

The self-priming process of self-priming pump was a very complicated gas-liquid mixed flow and separation process.In this article,a unsteady numerical simulation was applied to simulated the self-priming process of self-priming pump,with the initial condition was that the inlet and outlet pipe filled with air,and then self-priming time was estimated;The simulation results showed that gas inhaled into and discharged of the pump were mainly concentrated in the early stage of the self-priming process,the air void fraction reached up to 62.4% and 45.3%,respectively at the impeller inlet and the pump outlet in the initial stage;The change of air void fraction in the impeller inlet was more drastic than that of the pump outlet;In addition,self-priming performance was affected by the gap between impeller and guide vane,and the data showed a negative correlation between gap and self-priming time,which revealed the lager gap was beneficial to self-priming of the pump.

self-priming pump; self-priming process; gas-liquid two-phase flow; unsteady numerical simulation

1006-3080(2017)02-0280-06

10.14135/j.cnki.1006-3080.2017.02.020

2016-07-12

刘洪生(1990-),男,安徽人,硕士生,从事流体机械方向研究。

苏永升,E-mail:yssu@ecust.edu.cn

TH317

A