基于动力吸振器的中空轴系纵向减振研究*
赵 帅, 陈 前, 姚 冰
(南京航空航天大学机械结构力学及控制国家重点实验室 南京,210016)
基于动力吸振器的中空轴系纵向减振研究*
赵 帅, 陈 前, 姚 冰
(南京航空航天大学机械结构力学及控制国家重点实验室 南京,210016)
针对中空轴系的纵向振动,在轴系内部安置阻尼动力吸振器对其进行了减振设计。结合子结构综合法和传递矩阵法建立了附加阻尼动力吸振器复杂轴系的动力学模型,分析了阻尼动力吸振器与轴系的耦合系统在简谐激励下的动力学响应,并采用了有限元仿真,表明阻尼动力吸振器的加入使得轴系的纵向共振峰得到抑制,轴系共振频率附近的频响曲线趋于平缓。试验结果表明,附加阻尼动力吸振器后的轴系一阶纵向共振峰值下降显著,阻尼动力吸振器对轴系的纵向减振具有显著的效果。在中空轴系内部空间安装吸振器,既不占用多余的空间,又能获得较好的减振效果,可以作为船舶推进轴系纵向减振的一种新选择。
中空轴系; 纵向振动; 阻尼动力吸振器; 传递矩阵法; 子结构综合
引 言
随着船舶的大型化,大功率船舶越来越常见,推进轴系纵向振动对船舶动力系统的危害逐渐显现出来。纵向共振会影响推进轴系的寿命以及工作的可靠性。特别对于舰艇来说,严重的推进轴系振动会经过推力轴承基座传递到艇体,随之产生的二次激励力会造成艇体振动,并向水下辐射噪声,从而在艇体周围形成一个强大的辐射声场,降低舰艇的声隐身性能。所以,针对船舶推进轴系的纵向减振研究显得很有必要。
动力吸振器又称调谐质量阻尼器,通过在主系统上附加一个子结构,从而改变系统的振动状态,使得在特定的频段范围内减小主系统的振动响应[1]。动力吸振器结构简单,安装便利,所以在轴系上安装动力吸振器是减小船舶推进轴系纵向振动的有效方法。国外很早就开展了推进轴系纵向减振理论与试验研究。早在1960年,Goodwin[2]就提出用共振转换器来减小推进轴系纵向振动,由充满液压油的外接腔体和外接管系组成,采用的就是调谐吸振理论。本世纪初,Dylejko等[3-6]在Goodwin研究的基础上,继续开展了共振转换器对推进轴系纵向振动研究。Dylejko对共振转换器的减振效果进行了分析,并优化了其结构参数。Merz[6]则分析了共振转换器对轴系纵振所引起的水下辐射噪声的控制效果。近些年,国内学者也开展了运用共振转换器对轴系的纵向减振的研究。刘耀宗等[7]参考Dyleiko用功率流法分析了推进轴系纵向振动传递至艇体的能量,分析表明用轴向动力吸振器可以有效衰减一定频率范围内的纵向共振峰值。李良伟等[8]在Goodwin的基础上获得了动力吸振器参数的最优值。
上述的动力吸振器都需要安装在推力轴承基座上,而且是串联在纵振传递路径中,需要对结构变动较大。实际上,空心轴由于其在满足强度的要求下可以大量节约材料和减轻结构质量,早已广泛应用于船舶领域。基于这一特性,将动力吸振器安置于中空轴系内部可以作为轴系减振一种新的方式。本研究的目的在于探索内置式动力吸振器轴系减振的可行性和有效性以及设计方法。
针对中空轴系的具体结构特点,基于动力吸振器吸振原理,采用阻尼动力吸振器,并且安装在中空轴系内部空腔,结合子结构综合法和传递矩阵法建立了附加单个阻尼动力吸振器的复杂轴系的动力学模型;对由阻尼动力吸振器和轴系组成的耦合系统的纵向振动频率响应进行了理论分析,并采用有限元仿真进行了验证;最后设计制造了吸振器样件,验证了阻尼动力吸振器对轴系纵向振动的减振效果。
1 并联阻尼动力吸振器轴系的动力学模型
在探讨动力吸振器的减振效果时,通常将主振系简化为单自由度系统,但对于轴系而言,结构一般比较复杂以及冗长,要想获得更接近实际情况的减振效果,并不能将主振系简化为单自由度系统。对于单独的轴系连续系统,一般都采用传递矩阵法进行轴系的动力学响应计算,但只限制于链式的系统,即系统各个部件串联在一起。对于局部含有并联的子结构部件(吸振器)的复杂系统则无法直接利用传递矩阵法进行响应计算,结合子结构综合法和传递矩阵法来分析子系统对主振系的影响。简单来说,先将连续系统离散化成若干个单元,把含有子结构的单元作为一个二自由度系统,利用子结构综合法得到该单元与子系统在对接点的关系,再利用单元之间传递矩阵关系建立子系统与主系统各个单元之间的联系,进而可得到子结构对主系统任意单元的影响效果。
附加单个阻尼动力吸振器轴系的复杂系统如图1所示,将轴离散成p个单元, 阻尼动力吸振器安装在第i个单元位置处,轴系在单元j处受到激励力F0sin(ωt)。在附加阻尼动力吸振器的轴系中,对于轴系自身的主系统而言,吸振器质量块运动产生的惯性力会传递给主系统,相当于主系统在第i个单元的对接点上会产生一个附加的外激励力Psin(ωt),该激励力方向与主系统在对接点处的运动方向相反,频率相同。而对于由阻尼动力吸振器构成的子系统而言,其成为在基础位移激励下的单自由度运动。根据基础简谐激励的受迫振动理论,对接力P为
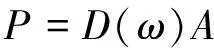
(1)
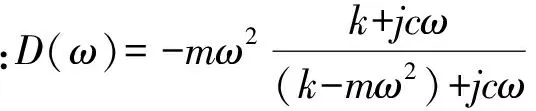
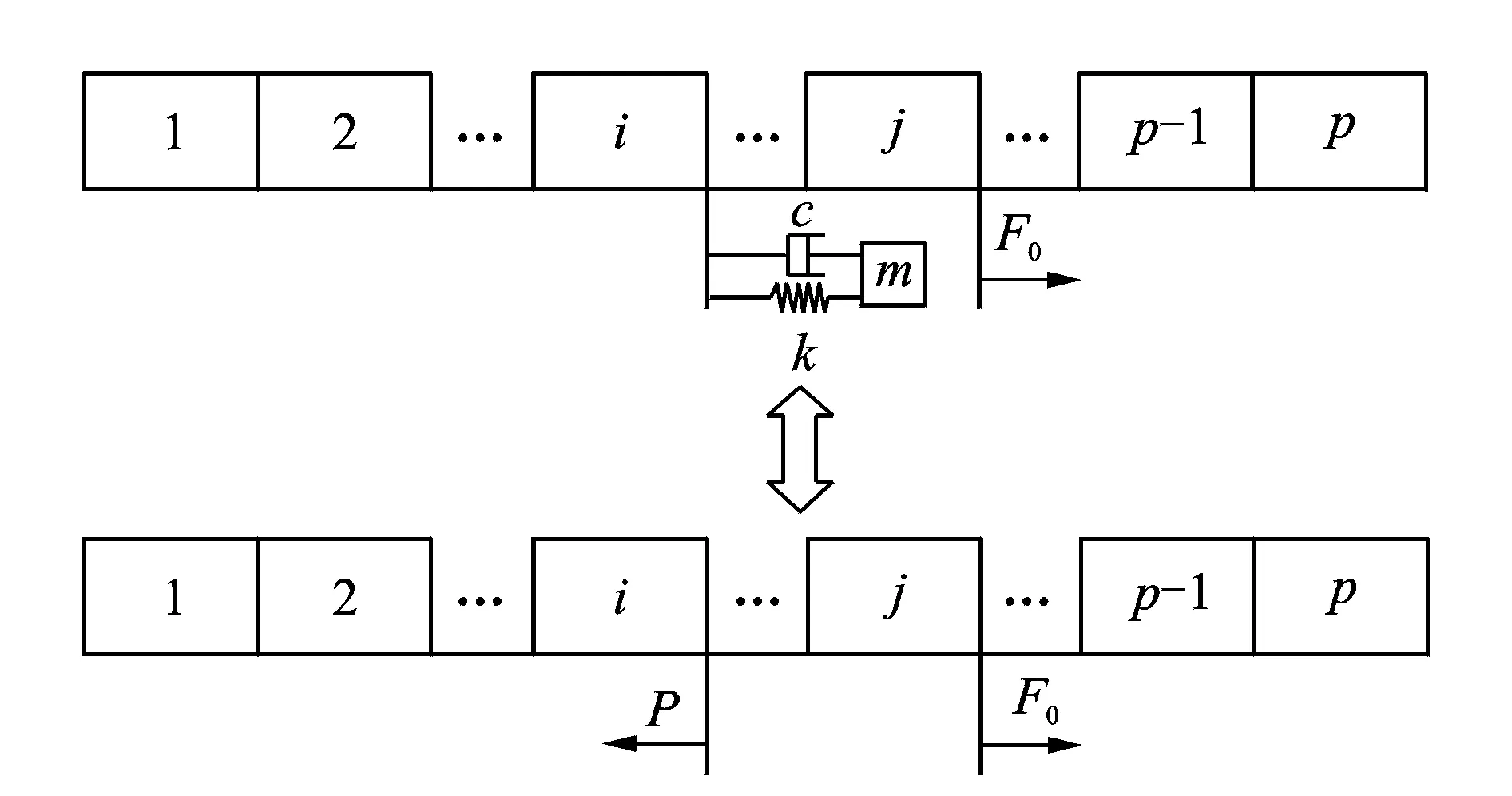
图1 附加阻尼动力吸振器后的简化模型Fig.1 Simplified model of a shafting with a damped DVA
加入吸振器后对接点的纵向位移可以表示为
(2)
其中:ui,F0为外力F0作用下单元i处的对接点产生的位移;ui,P为对接力P作用下单元i处的对接点产生的位移。
对于ui,P的求解需要得到对接力P,由式(1)可知对接力P为A的函数,故需要一定的推导得到对接力P的具体表达式。
对于轴系,定义轴系各单元的状态矢量为z=[X,N,1]T,式中X,N分别为位移和力。假设只在单元i处的对接点上施加单位力,第i个单元的传递矩阵可表示为
(3)

余下p-1个单元的传递矩阵则表示为
U0,k=
(k=1,2,…,i-1,i+1,…,p)
(4)
同样,对于在单元j处施加外力F0,第j个单元的传递矩阵可表示为
UF0,j=
(5)
余下p-1个单元的传递矩阵则表示为
UF0,k=
(k=1,2,…,j-1,j+1,…,p)
(6)
为了简化后续的理论推导,令
(7)
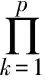
Tk=
(k=1,2,…,p)
(8)
结合式(3)、(4)可知,轴系仅在第i个单元受到单位力作用下,轴系系统的总传递矩阵可表示为
(9)
同样,结合式(5),(6)可知,轴系仅在其第j个单元受到外力F0作用下,轴系系统的总传递矩阵为
(10)
再令
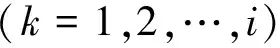
(11)
其中:Uk为轴段单元k的传递矩阵,表示为
(k=1,2,…,i)
(12)
则根据传递矩阵关系,可得到轴系仅在第i个单元受到对接力P作用下,对接点产生的位移为
(13)
同样,轴系仅在第j个单元受到外力F0作用下,对接点产生的位移为
(14)
将式(13)、式(14)代入式(2)可得到
(15)
由此可求得对接点的纵向位移为
(16)
将式(16)代入式(1)可得到对接力P
(17)
至此得到了P的具体表达式,则可知轴系在对接力P作用下的总传递矩阵为
(18)
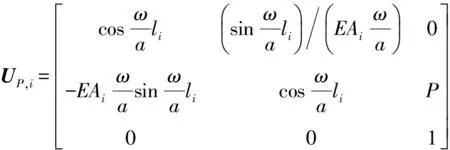
(19)
其余p-1个单元的传递矩阵表示为
UP,k=
(k=1,2,…,i-1,i+1,…,p)
(20)
通过式(18)可求得轴系在阻尼动力吸振器的作用下任意单元产生的位移,再由式(10)可求得轴系在外力作用下任意单元产生的位移。最后根据叠加原理即可求得吸振器和外力共同作用下轴系任意单元位置处的响应。对于自由-自由的边界条件,即X0,1≠0,N0,1=0,Xp,p+1≠0,Np,p+1=0,可得到轴系最左端的位移响应为
(21)
轴系最右端的位移响应为
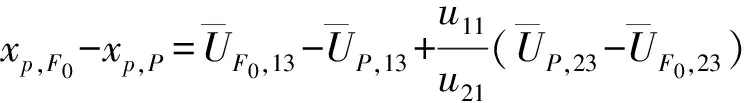
(22)
2 阻尼动力吸振器设计
图2为总长为5.7 m的中空阶梯轴,材料为45号钢(材料参数见表1),轴系各段的长度和内外径具体尺寸如图中所示,轴系的边界条件为两端自由。针对轴系的一阶纵向振动,利用中空轴系空腔,在其内部安置阻尼动力吸振器进行纵向减振。

图2 推进轴系尺寸参数(单位:m)Fig.2 Parameters of the hollow shafting(unit:m)
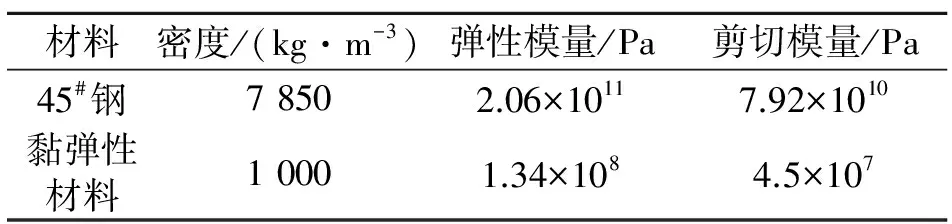
表1 材料参数
2.1 阻尼动力吸振器结构形式
阻尼动力吸振器是由圆柱形芯棒和黏弹性材料组成,如图3所示,芯棒提供吸振器所需质量,黏弹性材料则提供刚度和阻尼。其中芯棒的内、外半径分别为R0和R1,芯棒长度为l1,材料为45号钢。黏弹性材料的外半径为R2,总长度为l=2l2。
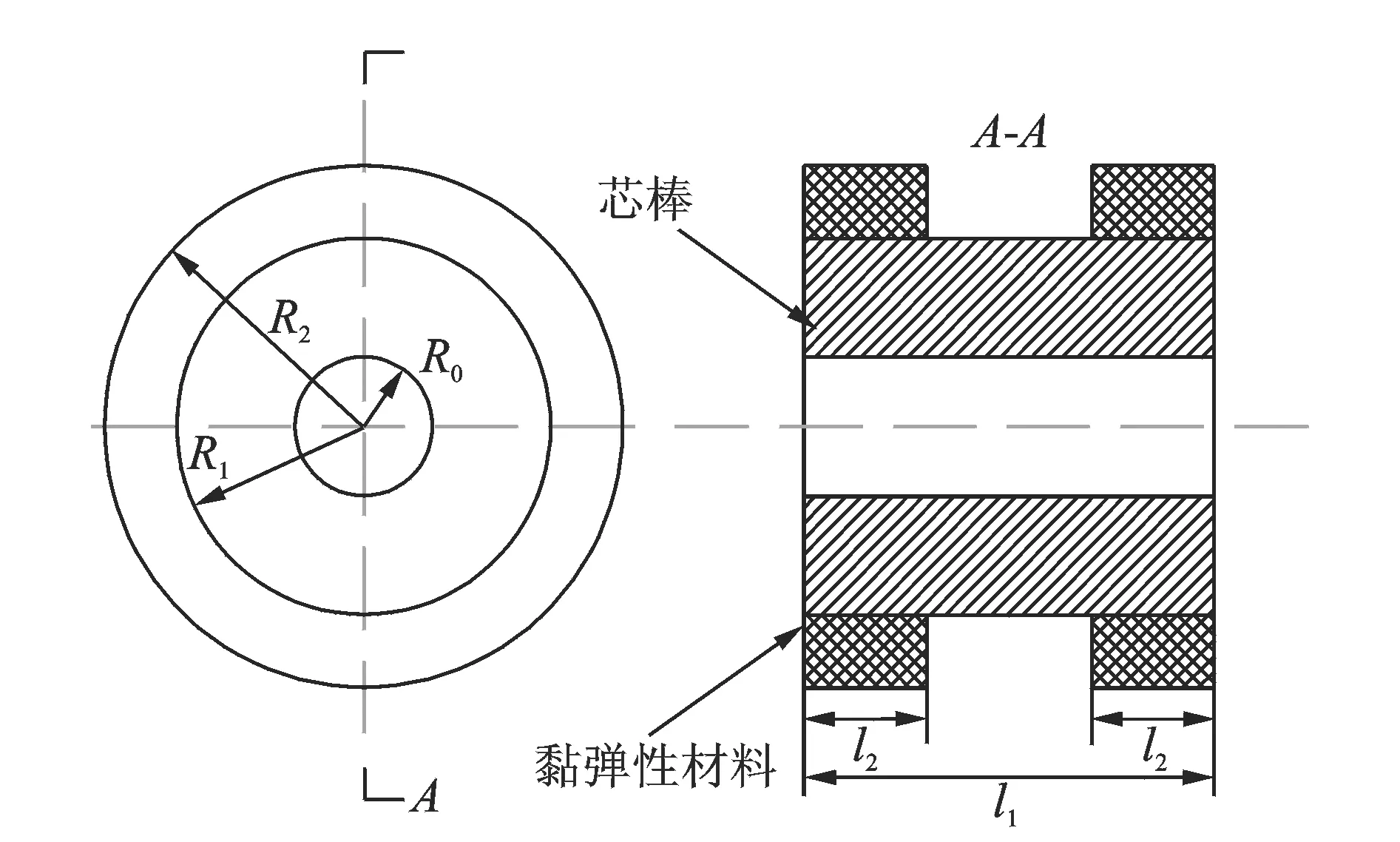
图3 吸振器结构示意图Fig.3 Schematic diagram of the dynamic vibration absorber (DVA)
当芯棒产生轴向位移,圆柱形黏弹性层将产生剪切变形,此时黏弹性材料层的纵向刚度[9]可以近似表示为
(23)
其中:R1和R2为圆柱形黏弹性材料的内半径和外半径;G为黏弹性材料的剪切模量;l为黏弹性材料的长度。
2.2 阻尼动力吸振器具体参数
为了获得良好的吸振效果,阻尼动力吸振器应尽量布置在振动响应强烈的地方。通过对轴系一阶纵振振型(图4)分析可知,阻尼动力吸振器可安装在轴系的左端部。
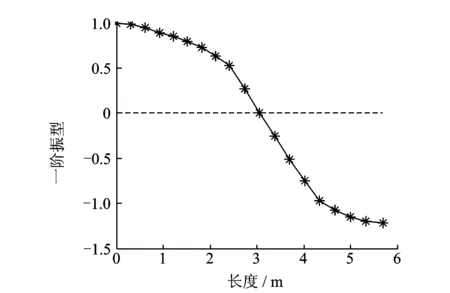
图4 轴系一阶纵振振型Fig.4 1st mode of longitudinal vibration of the shafting
将轴系按其第一阶纵振模态进行等效,根据能量等效原理[10],将轴系在各点处的总能量等效到吸振器安装位置处,可以计算得到轴系在吸振器位置处的一阶纵振等效质量为Meq=511.187 kg。由于吸振器的加入会引起轴系的横向变形,质量比不宜过大,综合考虑取吸振器的质量比为μ=3.8%,理论计算得到轴系一阶纵振频率为f1=424.5 Hz,根据最佳调谐频率比
(24)
吸振器固有频率设计为f=409 Hz。由芯棒和黏弹性材料的材料参数最终确定吸振器的具体尺寸参数如表2所示。

表2 吸振器尺寸参数
吸振器的最优阻尼比为
(25)
根据计算得到的最优调谐阻尼比ξopt=0.113,综上可得到吸振器的刚度参数为k=1.331×108N/m,吸振器的质量参数为m=19.57 kg,吸振器的阻尼系数为c=1.183×104N·s/m。
3 阻尼动力吸振器减振效果
吸振器的参数确定后,根据前两节的理论可以计算得到附加阻尼动力吸振器复杂轴系的动力学响应。计算时,在轴系的最右端施加单位纵向激励力。通过计算得到的阻尼动力吸振器加入前后轴系的原点位移频响曲线如图5所示,从图中可以看到,不加入阻尼动力吸振器的轴系在一阶共振频率(424.5 Hz)处出现一个很强烈的纵向共振峰。加入阻尼动力吸振器后,轴系的纵向共振峰得到抑制,使得频响曲线在共振频率附近趋于平缓,计算结果表明阻尼动力吸振器的加入对轴系纵向共振峰的控制效果十分明显。
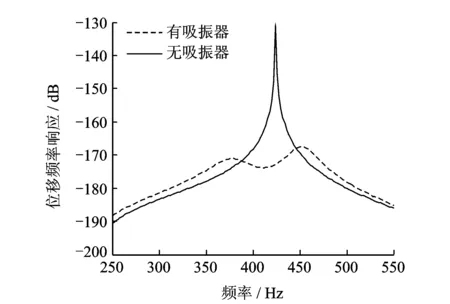
图5 轴系位移频响计算结果Fig.5 Calculated results of displacement FRF of the shafting
为了验证传递矩阵法计算的理论结果,采用有限元软件对理论计算模型进行了仿真,获得了吸振器加入前后的轴系位移频响曲线,结果如图6所示,图中可以发现理论计算结果同软件有限元仿真结果吻合良好,进而验证了上述理论方法的正确性。同时,吸振器的吸振效果也得到有限元计算的进一步证实。

图6 轴系位移频响计算和仿真结果比较Fig.6 Comparison between calculated and stimulated results of displacement FRF of the shafting
4 试验结果与分析
为了验证阻尼动力吸振器对轴系减振产生的实际效果,针对图2所示的中空轴系,制造了阻尼动力吸振器样件,并进行振动试验(图7)。阻尼动力吸振器的几何参数和材料参数同上节理论计算时的参数一致。需要说明的是,由于黏弹性材料的损耗因子会受到频率的影响,而黏弹性材料在实际条件下测得的吸振器的阻尼比为ξ=0.162,因此在调谐频率下吸振器的阻尼比无法满足最优阻尼比所要求的ξopt=0.113。阻尼动力吸振器安置在中空轴系的最左端,中空轴系安放在两个支撑架上,支撑架固定在地面上。纵向振动试验时,在中空轴系的右端面底部,用力锤进行纵向激励,以激励出轴系的纵向振动模态,并通过布置在轴系右端部的测点进行频率响应数据的测量。

图7 轴系试验Fig.7 Experiment of the shafting
图8给出了阻尼动力吸振器加入前后轴系的原点加速度频响曲线的试验结果。光轴在427 Hz左右有个强烈的纵向共振峰,同理论计算的424.5 Hz非常接近,进而也验证了轴系动力学建模的正确性。加入阻尼动力吸振器后,尽管吸振器的阻尼比无法达到最优值,轴系的纵向共振峰依然得到极大衰减,并且能够在较宽频带内实现轴系的纵向减振,表明阻尼动力吸振器对轴系的纵向减振效果十分显著。值得指出的是,由于试验时激励施加在轴系的下端面,从而施加的是一偏心激励力,所以试验中除了激励出了纵向振动模态,同时也激励出轴系的部分横向振动模态,故测得的频响曲线在纵向共振频率两侧也出现了峰值。另外,由于加入纵向阻尼动力吸振器后,吸振器的质量会对轴系的横向振动产生影响,从图中的试验结果可以看到,吸振器的加入使得横向振动固有频率有所下降。

图8 轴系原点加速度频响试验结果Fig.8 Experimental results of FRF of acceleration of the shafting
5 结 论
1) 对于附加阻尼动力吸振器轴系的复杂系统,通过子结构综合法将阻尼动力吸振器对轴系的作用简化成在对接点处的反作用力,再结合传递矩阵法计算得到吸振器-轴系耦合系统在任意位置处的动力学响应,进而能够分析阻尼动力吸振器的减振效果,可以为连续系统吸振器设计提供理论指导。
2) 轴系加入阻尼动力吸振器后,理论计算和有限元仿真都表明吸振器对轴系纵向振动减振效果十分突出,尽管试验条件下的阻尼动力吸振器并未达到最优阻尼比,轴系的纵向共振峰依然得到大幅度衰减。
3) 基于大型船舶推进轴系的中空特点,可充分利用中空轴系的内部空间安装阻尼动力吸振器,既可以获得良好的减振效果,又不增加对安装空间的要求,能够较好地适应工程要求,可以作为船舶推进轴系纵向减振的一种新选择。
[1] 曾胜,任意,程涛涛,等.利用调谐质量阻尼器进行管路系统减振[J].振动、测试与诊断,2012,32(5): 823-826.
Zeng Sheng, Ren Yi, Cheng Taotao,et al. Vibration suppression of pipe system with tuned mass damper[J]. Journal of Vibration, Measurement& Diagnosis, 2012,32(5): 823-826. (in Chinese)
[2] Goodwin A J H. The design of a resonance changer to overcome excessive axial vibration of propeller shafting[J]. Institute of Marine Engineers Transactions,1960,72:37-63.
[3] Dylejko P G, Kessissoglou N. Minimization of the vibration transmission through the propeller-shafting system in a submarine[J]. Journal of the Acoustical Society of America,2004,116(4):25-69.
[4] Dylejko P G, Kessissoglou N, Tso Y, et al. Optimization of a resonance changer to minimize the vibration transmission in marine vessels[J]. Journal of Sound and Vibration,2007,300(1-2):101-116.
[5] Dylejko P G. Optimum resonance changer for submerged vessel signature reduction[D]. Sydney:University of New South Wales,2007.
[6] Merz S, Kessissoglou N, Kinns R, et al. Minimization of the sound power radiated by a submarine through optimization of its resonance changer[J]. Journal of Sound and Vibration,2010,329(8):980-993.
[7] 刘耀宗,王宁,孟浩,等.基于动力吸振器的潜艇推进轴系轴向减振研究[J].振动与冲击,2009,28(5):184-187.
Liu Yaozong, Wang Ning, Meng Hao, et al. Design of dynamic vibration absorbers to reduce axial vibration of propelling shafts of submarines[J]. Journal of Vibration and Shock,2009,28(5):184-187.(in Chinese)
[8] 李良伟,赵耀,陆坡,等.减小船舶轴系纵向振动的动力减振器参数优化[J].中国造船,2010,51(2):139-148.
Li Liangwei,Zhao Yao,Lu Po,etal.Optimization of dynamic absorber parameters for reducing axial vibration of ship shafting[J]. Shipbuilding of China,2010,51(2):139-148. (in Chinese)
[9] Duan Yong, Wu Weiwei, Wang Fei. Tuned viscoelastic damper for hollow shaft longitudinal vibration control[J]. Journal of Ship Mechanics,2013,17(9):1066-1075.
[10]李玩幽,刘妍.动力吸振器优化设计中等效质量的简化求解法[J].集美大学学报,2000,5(3):50-53.
Li Wanyou, Liu Yan. Method of estimating equivalent mass in optimum design of vibration absorber[J]. Journal of Jimei University,2000,5(3):50-53. (in Chinese)

*江苏高校优势学科建设工程资助项目;中央高校基本科研业务费专项资金资助项目;江苏省普通高校研究生科研创新计划资助项目(KYLX-0242)
2015-01-20;
2015-04-03
10.16450/j.cnki.issn.1004-6801.2017.02.022
TB532; TH113
赵帅,男,1990年9月生,博士生。主要研究方向为振动与噪声控制。 E-mail:szhao-detec@nuaa.edu.cn 通信作者简介: 陈前,男,1951年11月生,博士、教授、博士生导师。主要研究方向为振动控制与故障诊断。 E-mail:Q.Chen@nuaa.edu.cn

