基于交易费用的信息控制投资组合模型

李阿娜,孙华东,景永强

(中北大学 理学院, 太原 030051)



基于交易费用的信息控制投资组合模型

李阿娜,孙华东,景永强

(中北大学 理学院, 太原 030051)

通过将信息风险函数引入投资组合模型，构建更加符合实际的带交易费用的信息控制模型，与传统的带交易费用的投资组合模型进行了比较，并且通过数学规划中的罚函数算法对模型进行求解，完成了模型的实证分析，验证了该模型和罚函数算法的有效性。

交易费用；数学模型；罚函数；信息控制；组合投资

从1952年马克维茨针对组合投资问题提出了均值-方差模型以来[1],最优化在组合投资问题中的应用已受到越来越多的研究人员及投资者的关注[2-8]。投资组合的组合优化模型可以降低投资中的非系统风险,达到分散风险的目的,然而针对具体的非系统风险构建的投资组合模型还较少[8-10]。因此,本文将非系统风险中的信息风险函数引入投资组合优化模型中,构建了带交易费用的信息控制投资组合优化模型,提出了改进的罚函数算法，并对模型进行求解,与传统的带交易费用的投资组合模型进行比较,验证了模型和算法的有效性。

1 带交易费用的投资组合模型

假设投资组合模型中的收益函数用线性函数来表示，加入交易费用函数后投资组合的收益比原来的投资组合的收益有所降低，由于资产交易过程中需要使用一部分收益用于支付交易佣金，则投资组合的收益函数表示为

g(x,r)=xTr-c(x)

其中：x表示资产的投资权重的向量；r表示资产收益率向量。

由于交易费用是从投资者的资本总额中扣除的，因此总的资本额的约束条件也发生了相应的变化，新的投资总额的约束条件可表示为

基于交易费用函数的投资组合问题可通过如下模型表示：

其中：向量x表示引入交易费用函数模型的资产配置权重；向量r表示每种资产的收益率；E(R)表示引入交易费用函数模型投资组合的期望收益，wi为第i种风险资产的单位交易费用； c(x)表示投资组合的交易费用函数； ck(xk)表示资产k所需交纳的费用。带交易费用的投资组合模型是含有绝对值函数的数学规划模型，由于绝对值函数是非光滑的，因此该模型为非光滑的二次数学规划模型。

2 带交易费用的信息控制投资组合模型

由于信息控制函数的变化量可导致投资者对投资组合进行相应的调整，进而影响整个组合投资的收益率，因此信息控制函数对资产收益率的影响可表示为

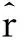
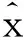
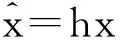
则总的资本额的约束条件也发生了相应的变化,引入信息函数后的投资总额的约束条件可表示为

带交易费用的信息控制投资组合模型可表示为：

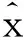
3 模型的求解

由于交易费用函数中含有非交易的绝对值函数，则带交易费用的信息控制投资组合模型为非光滑的二次数学规划模型，为模型的求解带来困难。针对非光滑的交易费用函数，可通过变换进行求解。

针对绝对值函数作以下变换，令

那么uk满足：

因此，带有交易费用函数的信息控制投资组合模型可转换为

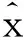
该模型为二次规划模型，本文通过罚函数算法进行求解。首先通过罚函数将带约束的模型转化为无约束的非线性规划模型，然后通过无约束规划问题的相应求解方法进行该模型的求解。

定义1 称

为带交易费用的信息控制投资组合模型的罚函数模型，

为上述的带红利的信息控制投资组合优化模型的罚函数，σ>0为罚因子，其中

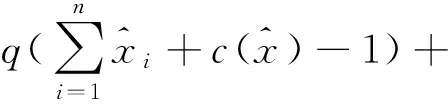
罚函数算法步骤如下：

步骤1 选定变量的初始点为x0；选取罚函数的初始罚因子σ1>0(可取σ1=1)，罚因子的放大系数c>1(可取c=10)；置k=1。

步骤3 若σkQ(x)<ε，则xk就是所要求的最优解，停止；否则转下一步。

步骤4 置σk+1=cσk；k=k+1，转步骤2。

因为惩罚项的特点，当k趋向于无穷大时，随着σk的不断增大，对每个不可行点的惩罚σkQ(x) 也将不断的增大并且趋向于无穷。所以，在对应于σk的约束极小化问题的最优解xk处，σkQ(x)的值应该是不断地减小，从而保证xk逐步趋向于可行并最终得到上述问题的最优解。

4 实证分析

对本文提出的带有交易费用函数的信息控制投资组合模型及其相应的罚函数算法进行数值实验和实证分析。依据行业背景和公司的成长性分析，选取大秦铁路(601006)、申能股份(600642)、青岛海尔(600690)、丰乐种业(000713)、华东医药(000963)、成霖股份(002047)、华神集团(000790)、如意集团(000626)8只股票进行实证研究。 收集这8只股票从2010年1月—2015年12月的月平均收益率(数据来源于www.ytarsc.com)，通过每种资产的历史资产收益的数据计算每只股票收益率的均值和方差。如表1所示，采用蒙特卡罗法进行每种资产收益率的数据模拟[11-12]。本文选取的模拟数据的样本数为30 000，模型中参数的初始化数据如表2所示。

表1 资产的期望与方差

表2 模型参数的初始化数据

1) 通过设定不同的投资者预期收益率，应用Matlab软件对带有交易费用的投资组合模型进行求解，计算结果如表3、表4和图1所示。将带交易费用的投资组合模型简记为CP模型。 表3为在投资者的预期收益率为10%时，通过计算得出的带交易费的模型的计算结果。表3表明在预期收益率一定时，通过配置风险较小、收益率较高的资产可达到投资组合的风险最小化。表4为带交易费用的模型在不同预期收益率下得到的投资组合的目标值，即风险值。 由表4和图1可知：随着预期收益率的增大，其相应的目标函数值也增大，符合收益越大风险越大的投资规律。表3、表4表明了本文提出的模型和算法的有效性，为投资者提供了一定的决策性参考。

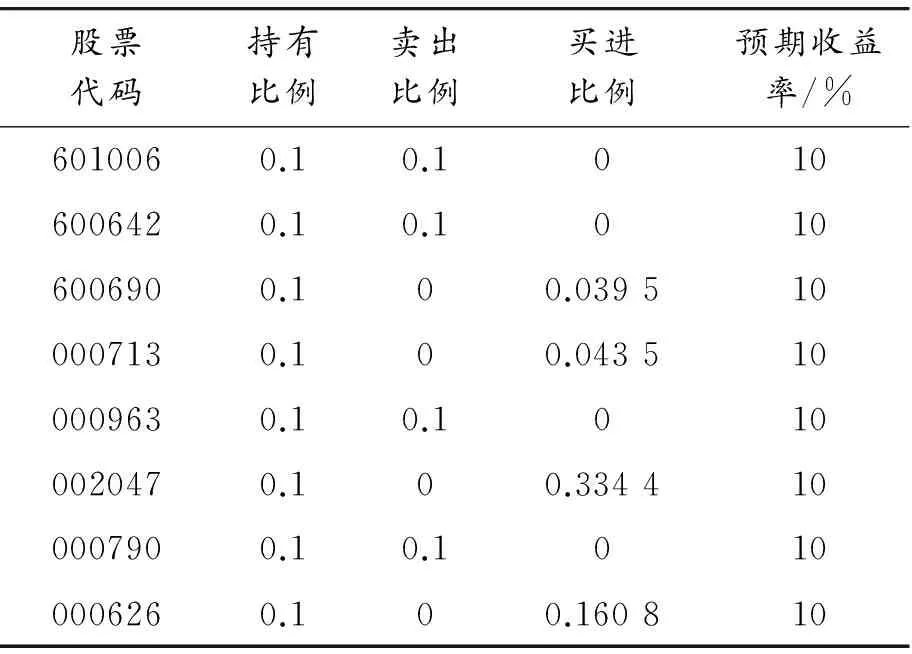
表3 带交易费的投资组合模型的计算结果

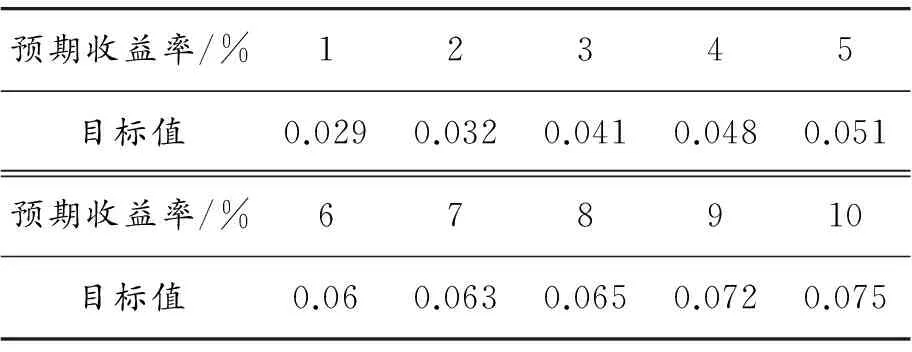
表4 不同预期收益率下CP模型的计算结果

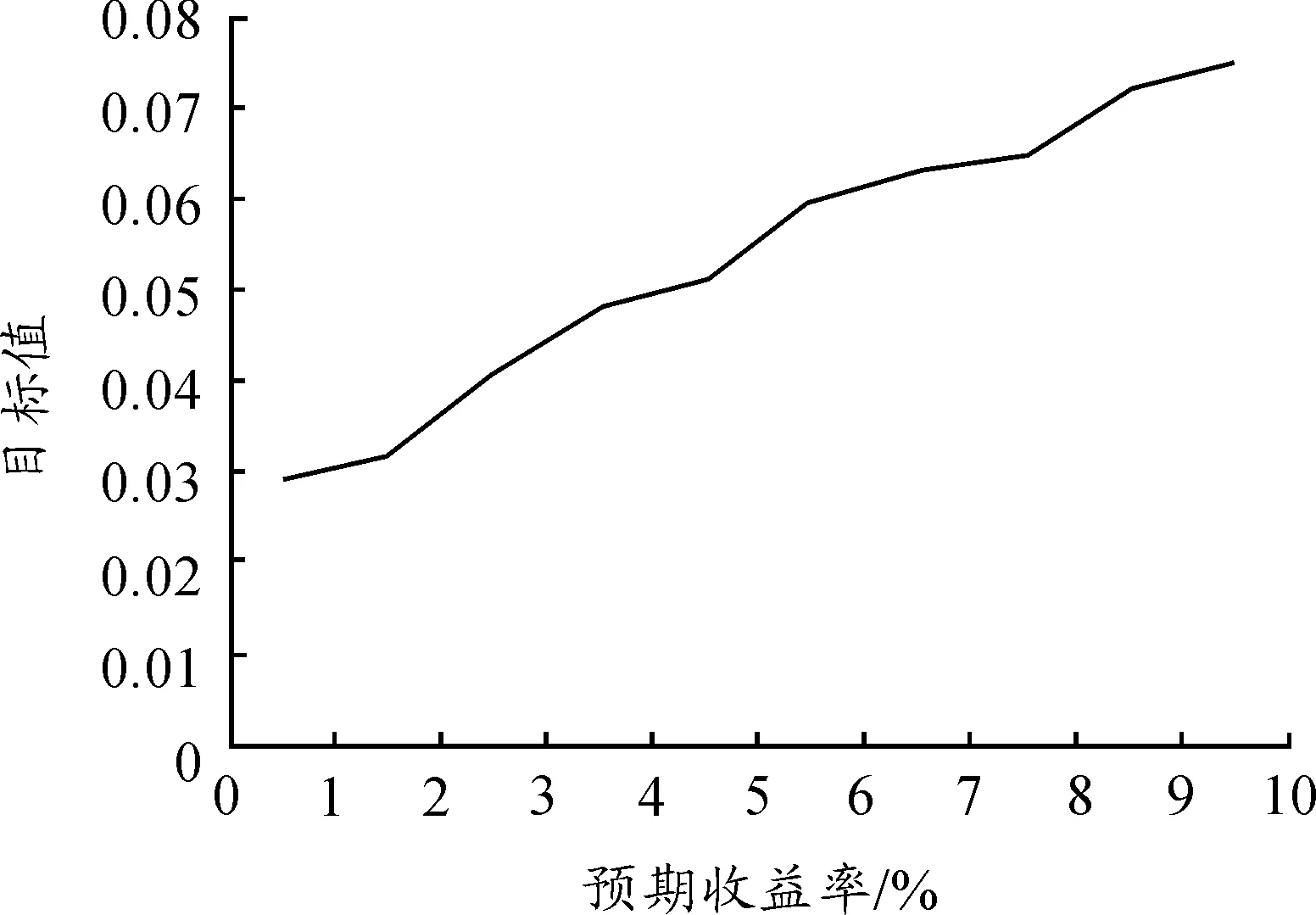
图1 不同预期收益率下CP模型的计算结果

2) 设定不同的投资者的预期收益率，通过Matlab软件对带交易费用的信息控制投资组合优化模型进行计算，结果如表5、表6和图2所示。将带红利的信息控制投资组合模型简记为CIP模型。

表5表示在投资者的预期收益率为10%时，通过Matlab计算的带交易费用的信息控制投资组合优化模型的结果，验证了该模型及其相应的罚函数算法的有效性。通过对比表3发现：带交易费用的信息控制模型具有较低的投资组合风险。投资者将带有不利信息的资产卖出，增持带有利信息的资产，从而获得风险更低的投资组合。通过设定不同的预期收益率，利用带交易费用的信息控制模型得到其相应的风险值，如表6和图2所示。表6表明：预期收益率越高，资产组合的风险越大，符合高风险高收益，低风险低收益的投资规律。通过对比表4和表6，发现带交易费用的信息控制模型更符合实际，能更好地为投资者提供投资决策。

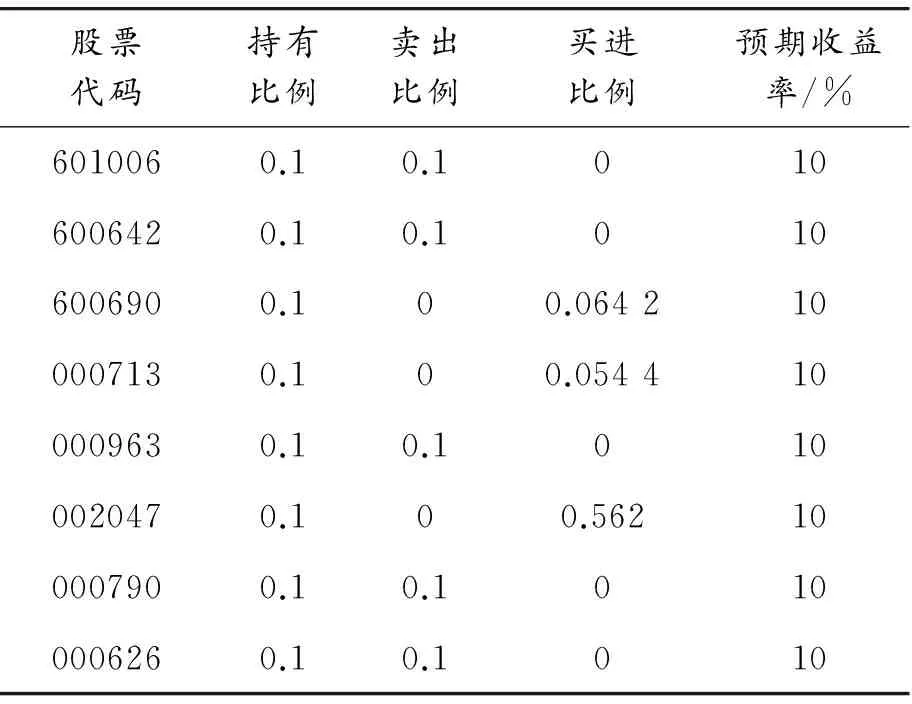
表5 带交易费用的信息控制投资组合

表6 不同的预期收益率下CIP模型的计算结果

图2 不同的预期收益率下CIP模型的计算结果

3) 通过设定不同的交易费用比例，应用matlab软件对带交易费用的信息控制投资组合模型进行求解，所得结果如表7和图3所示。结果表明：随着交易费用比例的增大，目标函数值在逐渐变小，资产配置的分散程度逐渐变小，由于交易费用的增大，资产收益降低，从而导致投资组合的风险值降低，且基于信息控制的投资组合模型比一般的投资组合模型具有更低的风险。

表7 不同的交易费用比例下CIP模型的计算结果

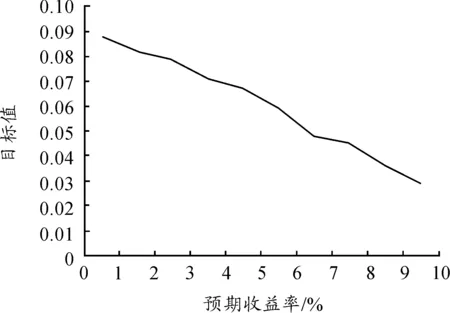
图3 不同的交易费用比例下CIP模型的计算结果

5 结束语

本文通过将信息风险函数引入投资组合模型，构建更加符合实际的带交易费用的信息控制模型，与传统的带交易费用的投资组合模型进行了比较，并且通过数学规划中的罚函数算法对模型进行求解。进行了模型的实证分析，验证了该模型和罚函数算法的有效性。实证分析结果表明：同传统的带交易费用的模型相比，带交易费用的信息控制模型具有较低的投资组合风险，且随着投资者预期收益率的不断提高，模型的目标值也逐渐增大，即投资组合的风险在逐步增加。

[1] HARRY M．Portfolio selection[J]．Journal of Finance,1952,7(1)：113-124.

[2] SHARPE W F.A Simplified Model for Portfolio Analysis[J].Management Science,1963,(3):13-26.

[3] EASTHAM J E,HASTING K J.Optimal impulse control of portfolios[J].Mathematical Programming,2008(4):11-24.

[4] 赵春峰.基于条件风险价值(CVaR)投资组合模型的分析及应用[D].成都:西南财经大学,2010.

[5] 梁素红.组合投资数学模型发展的研究[D].长春:吉林大学,2011.

[6] 王贞.几类投资组合优化模型及其算法[D].西安:西安电子科技大学,2012.

[7] 申飞飞,杨柳.基于CVaR的债券投资组合模型[J].经济数学,2014(2):56-59.

[8] 杨梅.凸规划和模糊线性规划模型在组合投资中的应用[J].统计与决策,2013(10):59-63.

[9] 张波,陈睿君,路璐.粒子群算法在投资组合中的应用[J].系统工程,2007,25(8):108-110.

[10]文凤华,马超群,陈牡妙,等.一致性风险价值及其算法与实证研究[J].系统工程理论与实践.2004,24(10)：15-21.

[11]BOUDOUKH J,WHITELAW R.The benchmark effect in the Japanese government bood market[J].Applied Mathematics and Computation,2009,(2):23-38.

[12]KONNO H,YAMAKAZI H.Mean-absolute deviation portfolio optimization model and its applications to Tokyo stock market[J].SIAM Journal on Optimization,2007(4):112-131.

(责任编辑 陈 艳)

Model of Portfolio Optimization Based on Information Control and Transaction Cost

LI A-na, SUN Hua-dong, JING Yong-qiang

(School of Science, North University of China, Taiyuan 030051, China)

This paper constructed a more realistic portfolio information control model with transaction costs and the information risk function, and the information control portfolio model with transaction costs was compared to the traditional portfolio model with transaction costs. The model was solved by the penalty function algorithm in mathematical programming. The validity of the model and penalty function algorithm was verified through the empirical analysis of the model.

transaction cost; mathematical model; penalty function; information control; portfolio

2016-01-12

电子测试技术国家重点实验室基金资助项目(9140C120401080C12)；中北大学科学基金资助项目(201406)

李阿娜(1989—)，女，山西运城人，硕士研究生，主要从事最优化模型及其数值方法研究，E-mail:454252140@qq.com; 孙华东(1965—)，男，教授，硕士生导师，主要从事弹塑性动力学、计算力学研究。

李阿娜,孙华东,景永强.基于交易费用的信息控制投资组合模型[J].重庆理工大学学报(自然科学)，2017(4):163-168.

format：LI A-na, SUN Hua-dong, JING Yong-qiang.Model of Portfolio Optimization Based on Information Control and Transaction Cost[J].Journal of Chongqing University of Technology(Natural Science)，2017(4):163-168.

10.3969/j.issn.1674-8425(z).2017.04.027

F830.59

A

1674-8425(2017)04-0163-06