基于蚁群算法的自动锁螺丝机路径优化方法

邓志强+++梁淑芬

摘 要：文章是介绍蚁群算法的应用，随着自动化技术的高速发展，自动锁螺丝机也被广泛的使用，然而对螺丝锁付路径没有得到合理的利用，针对目前螺丝锁付机器对螺丝锁付路径没有进行合理规划的问题，使用传统蚁群算法对螺丝锁付路径进行优化， 结合实际应用问题，通过模拟实验的方式，去调整群算法的参数设置，得到比较优化的结果。并给出了螺丝锁付优化路径图；实验表明该针对锁付路径的合理布局，螺丝锁付效率得到显著提高。

关键词：路径优化；蚁群算法；锁螺丝机

Abstract： This paper is to introduces the application of ant colony algorithm in the field of automation. With the rapid development of automation technology， the automatic locking screw machine is widely used. However， the screw locking method has not been used rationally. The algorithm of the ant colony algorithm is used to optimize the screw locking path， and the method of simulation is used to adjust the parameter setting of the group algorithm， and the result of comparison optimization is obtained. And the optimal path of screw lock is given. The experiment shows that the efficiency of screw locking is improved greatly.Keywords： path optimization； ant colony algorithm； lock screw machine

1 自动锁螺丝机路径问题描述

本文以XY-table型自动锁螺丝机为基准，设定每个螺絲孔为一个工位，则路径问题可以用数学图（Graph）来表示：V={c1，c2，c3，…ci，…cn}；i=1，2，…….n 是所有工位的集合，ci表示第i个工位，n表示工位的数目

E={（r，s）：r，s∈V}；表示所有工位之间的集合；

C={rrs：r，s∈V}；是所有工位之间连接的成本度量（工位之间距离）。

一个路径最优问题可以表达为：

求解遍历图G=（V，E，C），所有的节点一次都回到起始节点，使得到连接这些节点路径成本最低[1]。

2 蚁群算法简介

蚁群算法是对自然界蚂蚁的寻找路径的方式进行模拟得到的一个仿生物算法，是由意大利学者Marco Dorigo， Vittorio Maniezzo， Alberto Colorni 提出的一种模拟进化算法。

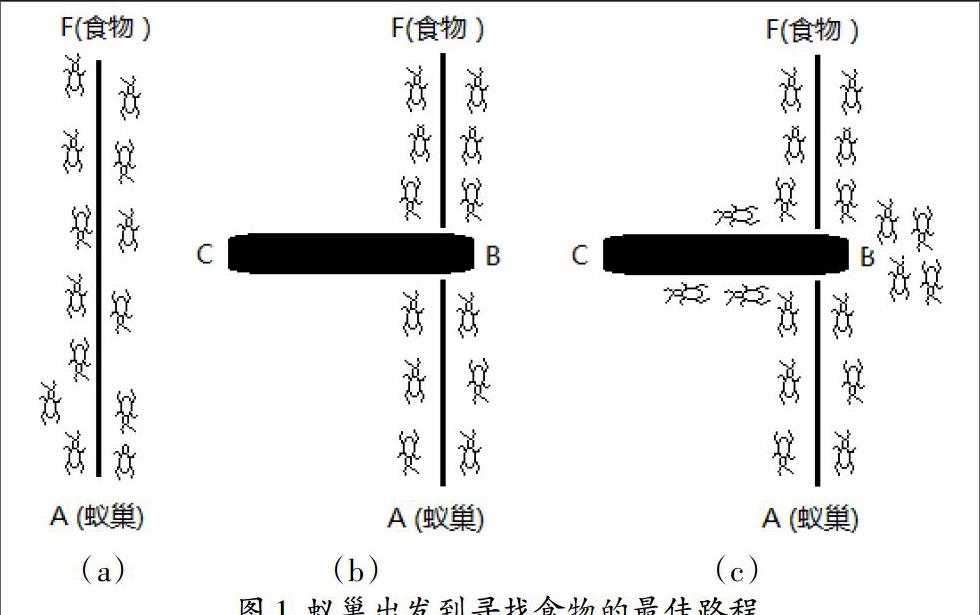
图1所示，一个真实的蚁群从蚁巢出发到寻找食物的最佳路程，不论有无障碍，蚁群总是可以找到从最优的路径。（a）没有蚂蚁从A到F（b）有障碍物的情况，蚂蚁到障碍物有不同的选择，而且选B或者选C是等概率的 （c）更多的蚂蚁选择B到目的。

蚂蚁在运动的过程中，可以在它自己所经过的路径一种信息传递的物质，被称之为信息素（pheromone）[2]是一种生物学激素，另外一蚂蚁同样可以感知到这种生物学激素，并且指导蚁群行进的方向。因此，大量的蚂蚁组成的这种群体行为可以表现出一种信息正反馈，当某一路径的蚂蚁越多，信息素浓度越大，被后续蚂蚁感知的概率就越高，因此选择该路径的直到整个种群找到最佳的路径。

为了更清晰的解释蚁群算的原理，先模拟一下蚂蚁搜索食物的具体过程。以图2为例说明，蚂蚁搜索食物的过程，信息素的浓度变化的过程，同时也是算法模拟的核心部分。

图2所示，ABF、ACF都表示蚂蚁的行进路程并且设定ACF的路程是ABF的两倍，（a）表示单次行走，（b）表示一个来回的示意图。设定每只蚂蚁的速度相同，目的地在F，蚂蚁从A点出发可以选择A-B-F或A-C-F路径。

设定以相同的时间行每一步，（a）图中，蚂蚁从A出发走ABF路线时，时间到达目的F用时记为1个单位时间，而走ACF路线同样的单位时间到C，只走完路程的一半。经过2倍单位时间的情况，走ABF路线的蚂蚁到达终点拿到食物又返回蚁巢，而走ACF路线的蚂蚁到达目的地。设定每只蚂蚁经过一处所留下的信息素为一个单位。经过4个单位时间后，所有从A出发的蚂蚁都取到食物并且返回，此时ABF路径已经往返了两次，每一处留下的信息素为4个单位，而经过ACF路线值往返了一趟，每一处的信息素为2个单位，其比值为2：1。寻找食物的过程继续进行，蚁群在A处派出蚂蚁，按照信息素的指导，ABF路线增加一只（共2只），ACF上仍未一只，再次进4个时间单位，ABF和ACF两条路径的信息素单位累计为12和4，比值为3：1，按照以上规则继续，ABF上增一只（共3只）而且ACF上仍然只有一只，再次经过4个时间单位，信息素的比值会变成4：1。继续进行，最终所有的蚂蚁会放弃ACF路线，而选择ABF路线。这个就是信息素的正反馈效应[3]。

3 算法的应用

假定算法中需要用到的机器蚂蚁数量为m，并且每个蚂蚁都用自己的内存，内存中有一个禁忌表（Tabu）用来存储蚂蚁已经到访过的位置，表示在以后的搜索中将不再会访问禁忌表中的标记，同时还有一个允许访问的工位标记表（Allowed）来存储蚂蚁可以访问的工位；另外还有一个矩阵（Delta）用来存储蚂蚁在一个循环中所经过的路径的信息素，所有工位之间的信息素用矩阵pheromone表示。最短路径bestLength，最佳路径为bestPath；设定NC_max为最大迭代次数。

3.1 初始化过程

设定在开始时刻，bestLength初始化为一个非常大的数（正无穷）[4]，bestPath数组为空。Allowed表中加入所有的工位节点并且设置所有蚂蚁的Delta矩阵为0，Tabu表为空。随机选取它们的起始位置，在Tabu表中加入初始工位（随机选取）节点，并且Allowed中去掉该节点。

3.2 算法在运行时选择下一个节点

算法要求遍历每个工位节点，选择下一个节点只能从Allowed表中某一概率（公式1）搜索到，每次选择到哪个工位节点，则把该工位节点加入到Tabu表，同时也必须从Allowed表中删除该节点，对于每只机器蚂蚁来说该过程重复（n-1）次，遍历所有的节点。此时，将初始节点加入到Tabu（禁忌）表中，Tabu表中这个时候的元素个数为n+1（n位螺丝孔个数），Allowed表中的标记全部清空，不允许任何节点被访问。 下一步按照（公式2）计算每只机器蚂蚁的Delta矩阵值并保存，最后计算出最佳路径，先比较每个蚂蚁的路径长短，然后和bestLength比较，如果其长度比bestLength小，则需要把该值赋值给bestLength，并且把Tabu（禁忌）赋值给BeatPath，即为最佳路径[8][9][11]。

3.4 结束条件

如果达到最大代数MAX_GEN，算法终止，转到第（5）步（输出最优值）；否则，重新初始化所有的蚂蚁的Delt矩阵所有元素初始化为0，Tabu表清空，Allowed表中加入所有的城市节点[10]。随机选择它们的起始位置（也可以人工指定）。在Tabu中加入起始节点，Allowed中去掉该起始节点，重复执行（2），（3），（4）步。

4 蚁群算法流程图

如图3所示，蚁群算法的简要流程：

5 基于蚁群算法对螺丝锁付路径的优化模拟

为了提高自动锁螺丝机的锁付效率，节省锁付时间，现使用蚁群遗传算法对自动螺丝机锁付的工件的30个螺丝孔螺丝路径进行路径优化，其中30个螺丝孔的工位坐标为

[45.2，14.15]；[76.85，9.49]；[107.42，18.4]；[178.31，130.62]；

[140.6，10.33]；[168.74，9.11]；[175.93，48.37]；

[196.92，132.6]；[150.3，142.16]；[140.96，133.49]；

[138.94，101.42]；[125.1，89.6]；[124.53，70.13]；

[99.96，61.23]；[97.41，78.1]；[77.6，92.35]；[49.88，54.29]；

[74.82，30.16]；[80.11，36.06]；[94.78，28.46]；[8.83，53.96]；

[27.46，86.3]；[29.4，114.1]；[38.76，86.59]；[41.34，122.96]；

[62.45，132.3]；[83.99，118.96]； [109.5，125.92]；

[136.26，118. 4]；[170.2，95.1]；

參数设置：

实验中，蚂蚁的最佳数目选择问题由Dorigo M 等提示了设计思路，由于实现过于复杂，本次实验采用相对比较简单的方式，即问题规模大致是蚂蚁数目的1.5倍时，蚁群算法的全局收敛性和收敛速度比较好[7]。由于目标为30，所有本次实验的蚂蚁的个数设定m=20，最大循环次数NC_MAX=300。

蚁群算法中各参数的作业是紧密耦合的，其中对算法性能起着关键作用的是信息素启发式因子？琢，期望启发式因子？茁和信息素挥发因子？籽三个参数。信息强度Q对算法的影响有赖于上述3个参数的配置以及对算法模型的选取，Q对算法性能的影响情况显然有较大的差异[12]，本文采用的是ant-cycle模型，试验是改变一个参数，其它参数不变的策略来探讨参数设置对蚁群算法的性能的影响，默认设置参数为？琢=1，？茁=1，？籽=0.3，Q=100，每组数据实验10次取平均值。实验得到的模拟结果如表1所示。

说明：在表1中，平均值表示将10次运行中每次得到的最短路径长度的平均值，最优值表示10次运行路径中的最小值，最差值表示10次运行得到的最大值，差值表示实验得到的最优与最差值字之间的差值。

分析表1得到以下可以参考的结论，最佳参数配置是？琢=1，？茁=5，？籽=0.3；在该蚁群算法中，？琢=1其它为默认值时，所得到的平均值比其它值得到的结果要好，此时差值是最小的，这说明解结果稳定且符合目标要求，？茁=5解的质量最高，超过5时，接结果远离最优，对应信息素挥发因子？籽值在0.1～0.5之间变化不大，取整0.3时接的结果质量最优。最优结果如图4所示。

以上分析是迭代300次运行下的试验结果，试验时还增加了不是最佳配置运行试验，结果表明，对于不是最优配置的实验，即使是增加运行次数得到的结果也不会有明显的改善。

因此，可以？琢=1，？茁=5，？籽=0.3最优配置为参考来结果不同目标实验结果，得到最优解，对于不同目标实验结果如表2所示。

6 结论

在目标个数不超过20个时不需要修改参数，就能快速的得到最优的结果，而且收敛次数很低。超过20个目标需要根据实际情况来微调？茁或者？籽的系数来得到最优的结果；实验验证在实际的应用中根据不同的目标需求需要具体分析才能得到最优的结果。

参考文献

[1]Othon Michail，Paul G. Spirakis. Traveling salesman problems in temporal graphs[J]. Theoretical Computer Science，2016.

[2]程冬保. 白蚁信息素研究进展[J]. 昆虫学报，2013（04）：419-426.

[3]段海滨.蚁群算法原理及其应用[M].北京：科学出版社，2005.

[4]A Hybrid Genetic Algorithm for the Traveling Salesman Problem with Pickup and Delivery[J]. International Journal of Automation & Computing，2009，01：97-102.

[5]Marco Dorigo，Ant Colony System：A Cooperative Learning Approach to the Traveling Salesman Problem

[6]M. Dorigo， V. Maniezzo， and A.Colorni， "The ant system： optimization by a colony of cooperating agents，" IEEE Transactions on Systems， Man， and Cybernetics-Part B， vol. 26，No.2pp.29-41， 1996.

[7]杜衡吉，李勇. 蚁群算法中参数设置对其性能影响的研究[J]. 现代计算机（专业版），2012，13：3-7.

[8]Zhi-Wei Ye；Zhao-Bao Zheng Research on the configuration of parameter alpha， beta， rho in ant algorithm exemplified by TSP，Proceedings of the International Conference on Machine Learning and Cybernetics， 2003，4；2106～211.

[9]Vasko， F J， Bobeck， J D， Governale， M A， Rieksts， D J， Keffer， J D，"A statistical analysis of parameter values for the rank-based ant colony optimization algorithm for the traveling salesperson problem" EN， 2011，Vol.62（6），pp.1169-1176.

[10]Tenbrink Thora， Wiener Jan. The verbalization of multiple strategies in a variant of the traveling salesperson problem.[J]. Cognitive Processing， 2009，10（2）.

[11]R. Moeini， M.H. Afshar，Constrained Ant Colony Optimisation Algorithm for the layout and size optimisation of sanitary sewer networks，Urban Water Journal， 2013，Vol.10（3），pp.154-173.

[12]葉志伟，郑肇葆. 蚁群算法中参数α、β、ρ设置的研究——以

TSP问题为例[J].武汉大学学报（信息科学版），2004（07）.

作者简介：邓志强（1991，01-），男，民族：汉，学历：硕士，方向：电子通信。