基于最小均方和递归最小二乘的有源滤波器谐波检测*

袁晓曦,彭 升

(1.武汉软件工程职业学院,武汉 430205;2.招商银行武汉分行,武汉 430012)

基于最小均方和递归最小二乘的有源滤波器谐波检测*

袁晓曦1*,彭 升2

(1.武汉软件工程职业学院,武汉 430205;2.招商银行武汉分行,武汉 430012)

针对当前有源滤波器谐波检测算法的精度低、运算量大、实时性差等不足,为了获得更加理想的谐波检测结果,提出了基于最小均方和递归最小二乘的有源滤波器谐波检测算法。首先针对锁相环获取输入信号运算量大、谐波检测时间长的难题,将过负载电流作为参考输入,加快有源滤波器的响应速度,然后基于最小均方算法和递归最小二乘算法快速、准确的实现谐波检测,最后在MATLAB 1204平台对本文算法的有效性和先进性进行了仿真验证性实验。实验结果表明,本文算法得到了较高的有源滤波器谐波检测精度,能够提高有源滤波器的补偿性能,而且具有较快的动态响应速度,改善了算法的实时性。

有源滤波器;谐波检测;过负载电流;最小均方算法;最小二乘算法

随着我国经济水平不断的增长,人们生活水平不断提高,大量的非线性负载在电网中投入运行,谐波含量不断增加,谐波问题出现的频率越来越高,对电网的电能质量产生不利影响,严重威胁到了电网的高效、安全运行,因此电力系统谐波治理已经成为当前一个重要研究课题[1]。为了有效解决谐波问题,当前主要有采用无源滤波器和有源滤波器APF(Active Power Filter),其中无源滤波器不仅运行成本高,而且谐波的滤波效果差[2],而APF可以对谐波进行自适应抑制,对各次谐波进行动态补偿,鲁棒性好,解决了无源滤波器存在的局限性,在电力系统谐波治理领域得到了成功应用[3-4]。

为了提高有源滤波器的工作性能,当前涌现了许多有效的有源滤波器谐波检测算法[5]。经典有源滤波器谐波检测算法包括瞬时无功功率理论和快速傅里叶变换[6],在实际应用中,它们均存在各自固有的缺陷,如瞬时无功功率理论的谐波检测性能与低通滤波器密切相关,而低通滤波器会导致信号的延迟和衰减,使谐波检测结果不稳定,有时检测精度过低[7];基于快速傅里叶变换的谐波检测算法需要对处理器的处理速度比较苛刻,使得它们的实际应用范围受限[8]。近些年来,自适应谐波检测算法由于具有实现简单,鲁棒性强等优点,受到了广大学者的高度重视[9]。当前自适应谐波检测算法参考输入采用余弦信号作为参考输入,使谐波检测的运算量大、实时性差,算法收敛速度慢[10]。

为了解决当前有源滤波器谐波检测算法的缺限,以获得更优谐波检测效果为目标,提出了基于最小均方LMS(Least Mean Square)和递归最小二乘RLS(Recursive Least Square)的有源滤波器谐波检测算法,实验结果表明,本文算法提高了有源滤波器谐波检测精度,动态响应速度更快。

1 最小均方和递归最小二乘的有源滤波器谐波检测算法

1.1 自适应谐波检测算法的工作原理

有源滤波器的补偿性能与谐波检测结果的优劣相关,而自适应谐波检测算法是一种有源滤波器检测算法,是有源滤波器能否正常工作的基础[11]。设i1(t)和ih(t)分别表示负载电流的基波和谐波,x(t)表示标准正弦信号,e(t)表示误差信号,那么自适应有源滤波器谐波检测算法的工作原理如图1所示。

图1 自适应谐波检测算法的工作原理

当电源电压理想,没有发生无畸变时,有:

us(t)=Ussin(ωt)

(1)

采用傅里叶级数对电网系统的非线性负载电流进行展开,可以得到:

=I1sin(ωt)cosφ1+I1sinφ1cos(ωt)+

(2)

式中:i1p(t)和i1q(t)分别表示基波的有功电流和无功电流;ih(t)表示高次谐波电流。

那么电网系统的畸变电流实际由基波无功电流和高次谐波电流组成,即有

id(t)=i1q(t)+ih(t)

(3)

自适应谐波检测算法的工作步骤为:

Step 1iL(t)包括基波电流i1(t)、ih(t),其中i1(t)可以看作为噪声部分,参考信号为锁相的正余弦信号x1(t)和x2(t)。

step 2 将iL(t)作为原始输入,与电网信号进行锁相同步后,输出为x(t)。

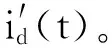
Step 5 采用最小均方差不断逼近id(t),主要通过对权值进行ω调节使输出信号的误差e(t)尽可能最小。

1.2 最小均方算法(LMS)

LMS算法是一种经典的自适应谐波检测算法,十分简单,而且具有较好的鲁棒性[12],其可以分为两种类型:定步长和变步长,其中定步长的LMS算法不能平衡谐波检测精度和检测速度之间的矛盾,而变步长的LMS算法的谐波检测性能,应用范围更广。LMS算法在工作过程是,不断根据期望和输出信号间的均方误差值对权值进行动态调整,尽可能使均方误差最小,最优ω对应的均方误差性能函数为

f(w)=ξ=E{e2(n)}

(4)

当均方误差性能函数的值最小时,自适应滤波器工作达到最佳。

LMS算法的迭代公式为

e(n)=d(n)-y(n)=d(n)-XT(n)W(n)

(5)

ω(n+1)=ω(n)+μe(n)X(n)

(6)

式中:X(n)表示输入信号矢量,ω(n)表示权值系数向量,μ代表步长。

1.3 递推最小二乘法

递推最小二乘法又称之为最小二乘算法(RLS),可以直接根据相关数据来找到最优的滤波,相对于最小均方算法,RLS算法可以获得更加理想的最佳滤波器[13],其中2个比例因子k1(n),k2(n)的计算公式如式(7)和式(8),其工作流程参考文献[14]。

(7)

(8)

1.4 本文的谐波检测算法

在传统的自适应谐波检测算法中,输入参考信号通常和基波相关联,没有考虑谐波的影响,因此为了获得理想的输入信号,通常情况下根据锁相环得到电网的电压相位,然后构建与该相位一致正余弦信号,由于锁相环本身的内部结构复杂,导致计算运算量非常大,降低了谐波检测效率,使有源源滤波器补偿实时差。

为了解决该难题,本文直接没有利用锁相环的电网电压相位,而时直接将三相负载电流iLa,iLb,iLc进行Clark坐标变换,产生正交信号iLα,iLβ作为输入信号,使谐波检测的动态响应时间明显缩短。本文谐波检测算法的工作步骤如下:

(1)将过负载电流作为参考输入,加快有源滤波器的响应速度。

(2)最小均方算法实现有源滤波器的谐波检测.

(3)采用递归最小二乘算法实现有源滤波器的谐波检测。

(4)对最小均方算法和递归最小二乘算法进行自适应加权,得到最优的有源滤波器谐波检测结果。

2 实验结果与分析

2.1 实验参数

为了全面分析基于最小均方和递归最小二乘的有源滤波器谐波检测算法的有效性和优越性,采用MATLAB 2104工具箱进行了仿真实验,并编写了具体的源滤波器谐波检测算法程序,其中仿真实验的参数设置具体见表1。

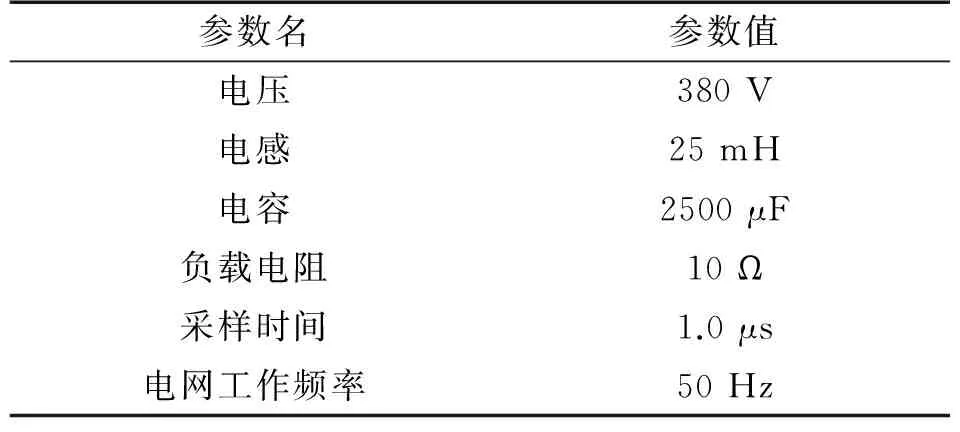
表1 仿真实验的相关参数设置

2.2 结果与分析

2.2.1 电网电流的波形的分析

对于电网系统,当负载发生变化时,没有补偿和补偿后电网电流波形的变化曲线如图2和图3所示。对图2和图3进行对比分析可以发现,当负载发生突变时,无有源滤波器补偿的情况下,电网电流波形幅度大,极不平稳,没有达到标准正弦波状态,电流畸变严重;而经过有源滤波器补偿后,电网电流的变化十分平稳,有规律,周期性十分明显,而且电流畸变率大幅度下降,获得了更优的电网电流,从而证明了本文算法的有效性。

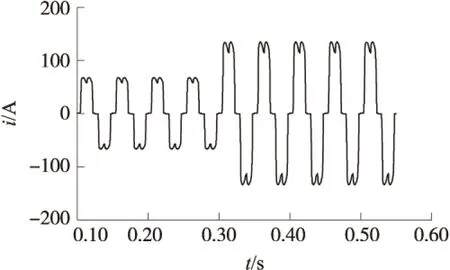
图2 补偿前的电网电流波形

图3 补偿后的电网电流波形

2.2.2 基波电流波形和谐电流波形的分析

本文算法的基波电流波形和谐波电流波形输出结果如图4和图5所示。

图4 本文算法的基波电流波形检测结果

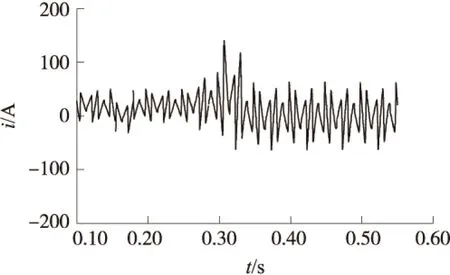
图5 本文算法的谐波电流波形检测结果

从图4和图5可以知道,当负载突变发生变时,本文算法设计的自适应滤波器可以及时、准确检测到突变状况,在很短时间使基波电流波形和谐波电流波形达到稳定状态,算法的收敛速度明显加快,显示较好的鲁棒性,电网的电能质量得到改善,保证了电网能够的高效、安全的运行。

2.2.3 与传统算法的性能比较

为了使本文算法的有源滤波器谐波检测结果更具说服力,在参数相同条件下,实验环境不变的情况下,采用传统算法[13]进行对比实验,其基波电流波形和谐波电流波形输出结果如图6和图7所示。

图6 传统算法的基波电流波形

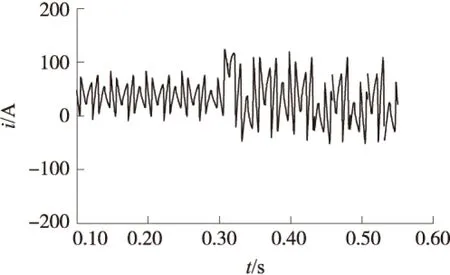
图7 传统算法的谐波电流波形

对图6和图7的实验结果进行分析可以发现,当负载突变发生变时,传统算法设计的应滤波器的响应速度慢,在较长一段时间使基波电流波形和谐波电流波形达到稳定状态,比本文算法的收敛速度要慢一倍,无法保证了电网系统的工常的运行,对比结果说明了本文算法提高了有源滤波器谐波的检测精度,获得较好的有源滤波器补偿性能,很好地兼顾稳态精度与收敛速度,而且具有较快的动态响应速度,可以满足有源滤波器谐波检测的实时性要求,从而证明了本文算法的优越性。

3 结束语

在有源滤波器的实际应用中,动态响应速度和检测精度十分关键,而传统自适应谐波检测算法存在计算时间长,动态响应慢等不足,在分析当前有源滤波器谐波检测检测研究现状的基础上,提出了基于最小均方和递归最小二乘的有源滤波器谐波检测算法。将过负载电流作为参考输入,避免采用余弦信号作为参考输入的不足,然后采用最小均方算法和递归最小二乘算法进行谐波检测,MATLAB 2014平台的仿真实验结果表明,本文算法加快了提高了谐波检测的动态响应速度,降低了计算时间复杂度,改善了有源滤波器的补偿性能,获得理想的有源滤波器谐波检测结果,具有广泛的应用前景。

[1] 姜齐荣,赵东元,陈建业. 有源滤波器——结构原理控制[M]. 北京:科学出版社,2005:1-7.

[2] 呼小亮,谢钊文,李学锋,等. 一种有源滤波器电流环控制的新方法[J]. 电气传动,2015,45(2):35-38.

[3] 范瑞祥,罗安,涂春鸣. 井联混合型有源滤波器的分频控制方法研究[J]. 中国电机工程学报,2007,27(25):108-113.

[4] 高鹰,谢胜利. 一种变步长LMS自适应滤波算法及分析[J]. 电子学报,2001,29(8):1094-1097.

[5] 李辉,吴正国,邹云屏,等. 变步长自适应算法在有源滤波器谐波检测中的应用[J]. 中国电机工程学报,2006,26(9):99-103.

[6] 工振浩,吴杰,工晓冲,等. 有源滤波器任意指定次谐波电流检测和控制策略[J]. 电气传动,2008,38(1):77-80.

[7] 翟瑞淼,英超,任国臣,等. 基于Nuttall窗的三峰插值谐波算法分析[J]. 电力系统保护与控制,2015,43(10):38-43.

[8] 杨秋霞,梁雄国,郭小强,等. 准谐振控制器在有源滤波器中的应用[J]. 电工技术学报,2009,24(7):171-176.

[9] 吕广强,刘 娱,段海军. APF中一种改进的变步长LMS自适应谐波检测算法[J]. 电力系统保护与控制,2016,44(7):96-101.

[10] 宋志雄,喻翌,赵海全. 基于箕舌线函数的变步长自适应谐波电流检测算法[J]. 电力系统自动化,2013.37(22):54-58.

[11] 陈欢,何怡刚,肖建平,等. 基于CWT和DWT相结合的谐波检测[J]. 电力系统保护与控制,2015,43(20):71-75.

[12] 刘心旸,王杰. 基于瞬时无功功率理论的自整定因子变步长低通滤波器研究[J]. 电力系统保护与控制,2012,40(10):84-89.

[13] 杨建宁,陈捷,关佳军,等. 一种改进变步长的自适应谐波检测算法[J]. 电力系统保护与控制,2011,39(16):40-52.

[14] 郑征,杜翠静,常万仓. 三相不对称系统中谐波电流检测的新方法[J]. 电力系统及其自动化学报,2010,22(3):50-54.

Harmonic Detection of Active Power Filter Based on Least Mean Square Algorithm and Recursive Least Square Algorithm*

YUANXiaoxi1*,PENGSheng2

(1.Wuhan Vocational College of Software and Engineering,Wuhan 430205,China;2.China Merchants Bank Wuhan Branch,Wuhan 430012,China)

Current active filter harmonic detection algorithms have defects as low detection accuracy,big computation quantity,and poor real time and so on,in order to obtain more ideal harmonic detection results,a novel harmonic detection algorithm of active power filter was proposed based on least mean square algorithm and recursive least square algorithm. Firstly,the load current is taken as reference input to solve the problem of large amount input signal and harmonic detection time long for the phase locked loop and accelerate the response speed of the active filter,and secondly fast and accurate harmonic detection results are achieved based on least mean square algorithm and recursive least squares algorithm;finally,the effectiveness of the proposed algorithm is simulated and verified in the MATLAB 1204 platform. Experimental results show that the proposed algorithm can obtain higher harmonic detection accuracy,can improve the compensation performance of active power filter,and it has fast dynamic response speed,and improves the real-time performance.

active power filter;harmonic detection;least mean square algorithm;recursive least square algorithm

项目来源:2014年湖北省教育厅科学技术研究项目(B2014211)

2016-03-20 修改日期:2016-08-28

C:1270

10.3969/j.issn.1005-9490.2017.02.025

TM352

A

1005-9490(2017)02-0386-04