基于CIC滤波器和madζ检测法的多频脉冲信号检测与估计

孙 昕，张世海

（中国人民解放军91439部队 辽宁 大连116041）

基于CIC滤波器和madζ检测法的多频脉冲信号检测与估计

孙 昕，张世海

（中国人民解放军91439部队 辽宁 大连116041）

在多频脉冲信号检测与估计的算法中，通过采用三级CIC滤波器实现对多个频率脉冲信号的快速检测，采用传统的能量检测和madζ法联合检测的方法实现了信号频率等参数的准确估计。实验验证该算法满足在复杂背景噪声下可靠地检测多频水声脉冲信号，数据处理算法的有效性得到了验证。

检测；估计；CIC滤波器；madζ法；多频脉冲信号

当水声信号检测背景受到海洋环境噪声、平台运动噪声、平台的高速运动引起多普勒频移以及多途干扰等组成的多种因素影响，实现对多个频点不同，到达时序和幅值也不同，且接收时间上可能有混叠的脉冲信号的快速检测和参数估计将十分困难[1]。

级联积分梳状滤波器（Cascade Integrator Comb，CIC）是一种特殊的FIR滤波器，具有通带平坦，旁瓣非常低，比传统的FIR滤波器更加有效等优点[2]。为满足多个频点且接收时间上可能有混叠的脉冲信号检测，采用多组多级CIC滤波器级联的信道化划分技术[3]，其基本原理是对接收带宽范围内的全频带信号进行分割，即用一组性能相同的带通滤波器组将全频带划分为一系列的子频带。滤波器组对各个子频带的输出反映了信号的频率信息，且采用滤波器组的方法能够提高每个信道内信号的信噪比，具有对每个目标的脉宽和周期进行估计的优势，满足对多个频点的脉冲信号的快速检测与估计，在多个信号混叠时也能准确检测。

信号瞬时频率估计是通过复相关计算的信号短时谱重心ζ获得的。向大威教授等提出的短时谱重心方法（madζ检测法）是一种新的信号检测方法[4]。所谓短时谱重心，就是从有限时间段内的数据得到的谱重心，对每个时刻，信号短时谱重心ζ的估计是一个随机起伏量。对信号短时谱重心ζ加权平均，可以得到信号频谱的中心频率（载频）的估计值。在脉冲信号的形式未知，信号频率等参数亦未知条件下对整个信号进行参数的准确估计，首先应对信号的到达时刻进行估计，对通过CIC滤波器组的信号求包络幅值并与动态能量门限比较，即可以得到检测信号窗口，进而估计出信号到达、结束的时刻。根据信号到达及结束时刻和相邻两个脉冲的信号到达时刻，可以得到信号的脉宽和周期的估计值，并确定接收信号包络幅值，进而得到多频脉冲信号各参数。

1 级联积分梳状滤波器的设计

1.1 级联积分梳状滤波器（CIC滤波）

CIC滤波器是一种基于零极点相抵消的FIR滤波器[4-7]，它由积分器（Integrator）和梳状器（Comb）两部分组成，其结构图如图1所示[8]。

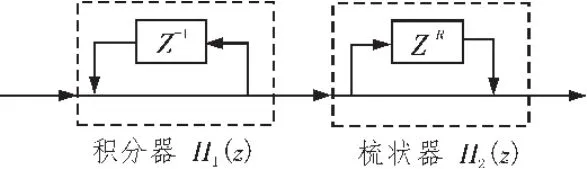
图1 CIC滤波器结构图

级联积分梳状滤波器的z域传输函数为:

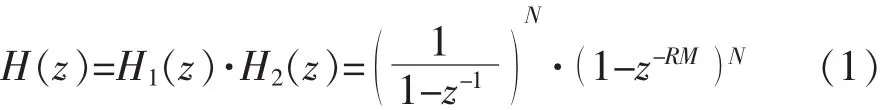
其中级联积分器的传输函数为H1（z），

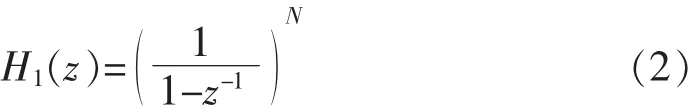
级联梳状滤波器的传输函数为H2（z），

在上述式中，N为积分梳状滤波器的级联数，R为数字变频中的抽样率或插补率，M是为调整滤波器特性而设置的调整因子，R、N、M为取值1，2，3，4……的自然数。

CIC滤波器具有通带平坦、阻带低、抗混叠效果好，不需要太高的阶数就能满足性能指标，比传统的FIR滤波器更加有效等优点[9]。应用CIC滤波器可实现多频点脉冲信号的前、后沿快速检测。由于多级CIC滤波器的旁瓣抑制好，因此实际应用中采用多级CIC级联。

信号前沿快速检测中，为了满足前沿检验时延要求，将接收信号下变频到零频，使用8 kHz全频带的三级CIC滤波器进行滤波降噪，后经过幅度门限法获取到信号，立即转发。其幅频特性图如图2所示。其中暗色白线分别对应一级、二级和三级的CIC滤波器幅频特性曲线，高亮白线为联合后的滤波器幅频特性曲线。从图中可以看出，通带内非常平坦，旁瓣降至-100 dB。

1.2 信道化划分的多级CIC滤波器

在实际应用中，为了解决同时发射多频点但幅度不同的信号检测问题，建立多个1 kHz带宽的滤波器组，对接收信号分别进行动态门限检测确定信号结束时刻。这种机制满足了实时检测的需要，又大大降低漏报率。在具体实现上是将接收信号通过与各子带中心频率正交变频，再低通滤波获取到差频信号，然后再进入到带宽为1 kHz的CIC滤波器中处理。图3是带宽为1 kHz的三级CIC滤波器幅频特性图。从图中可以看出，通带内非常平坦，旁瓣降至-120 dB，很好的抑制了子带间信号串漏，有益于信号检测与判断。

图2 带宽8kHz的CIC幅频特性

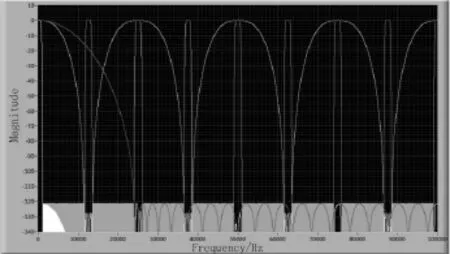
图3 带宽为1kHz的CIC幅频特性

2 短时谱重心（madζ）检测法

2.1 短时谱重心方法

短时谱重心方法是一种新的信号检测方法，向大威教授在文献[10]中对短时谱重心法进行了详细的数学推导。当检测的背景是由海洋噪声、目标噪声以及各种干扰相叠加时，采用动态能量检测方法将十分困难[11-12]；由于在高信噪比时，短时谱重心起伏较小，而在低信噪比（或无信号）时，短时谱重心起伏很大。信号瞬时频率的估计是通过复相关计算的信号短时谱重心ζ获得的。所谓短时谱重心，就是从有限时间段内的数据得到的谱重心，对每个时刻，信号短时谱重心ζ的估计是一个随机起伏量。信号接收机输出的短时谱重心是不断起伏的，起伏在高信噪比时会变得很小，而在低信噪比时会变得很大。由于起伏的绝对偏差移动平均madζ可以用来度量起伏的大小，因此它可以被用来检测信号。对信号短时谱重心ζ加权平均，可以得到信号频谱的中心频率（载频）的估计值，再通过瞬时频率估计后得到的频率-时间曲线，就可以估计出信号的调制方式。madζ是短时谱重心绝对偏差的移动平滑值，它可以用来衡量谱重心在不同时间的起伏大小。实际上，短时谱重心起伏就是频率起伏，起伏的大小与信噪比有关。若用一个频率值当作门限。能够可靠地检测信噪比高于某一个特定值的信号，而排除低信噪比的多途干扰以及噪声。使用这种新的检测方法，在海洋噪声、目标辐射噪声以及小的多途干扰背景中，能可靠地检测信号，并能同时对信号的一些参数作出估计。

2.2 算法实现

接收机接收的信号为r（t），其由信号s（t）和噪声n（t）组成，接收机的实输出r（t）经过希尔伯特变换就可以得到。由于r（t）和是互相正交的，因此通称它们是接收机的正交输出。利用这两个正交的分量可以组成接收机的复输出γ（t），即接收机的输出的解析形式为[13]：

根据复相关函数的定义[14]，接收机复输出γ（t）的复相关函数R（τ）可以表示为

复相关函数R（τ）还可以表示为极坐标形式：

上式中Φ（τ）是R（τ）的幅角，即：

按照一阶原点谱矩的定义[15]，其一阶原点谱矩可以表示为：

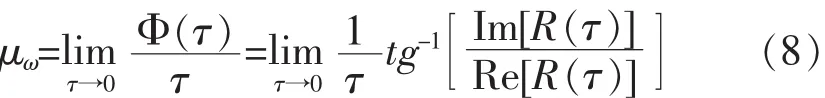
由此得到

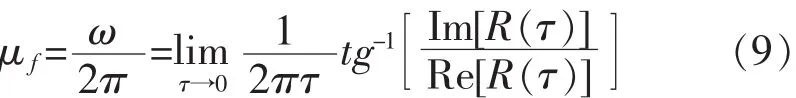
在实际应用中无法利用谱重心。因为要得到精确的谱重心需有非常长的数据。然而，可以采用短时谱重心来代替谱重心。所谓短时谱重心，就是从有限时间段内的数据得到的谱重心。此时，短时谱重心就不再是一个常量，而是一个随机起伏量。短时谱重心用来表示，其单位就是频率的单位。频率通常用英文字母f来表示。因此，为了书写方便，我们用希腊文的字母ζ来代表短时谱重心，即，如果ζ是平稳随机起伏的，而数据长度是一个非常大的数N，则ζ的平均值为，其标准偏差值。如果ζ是非平稳的，数据长度N有限，就应当用移动平滑来代替平均。此时，用移动平滑来代替平均而得到ζ的短时均值为，其对应的偏差值为dζ（n）=ζ（n）-mζ（n），为了避免在计算标准偏差时出现平方与开方运算，将用绝对偏差的移动平滑值来代替标准偏差，即

而madζ就是短时谱重心绝对偏差的移动平滑值，它可用来衡量谱重心在不同时间的起伏大小。

3 多频脉冲信号处理流程

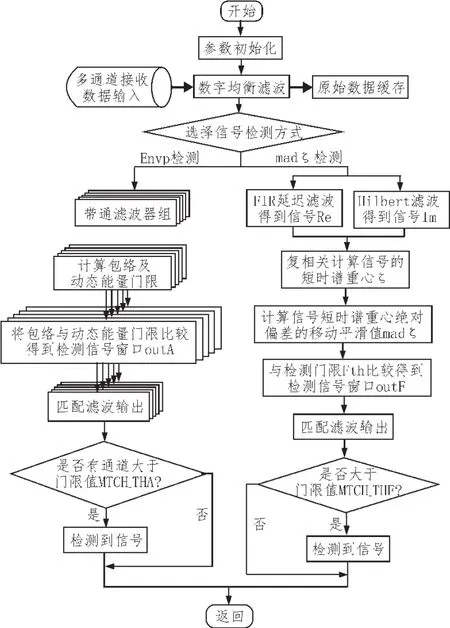
图4 信号检测算法流程

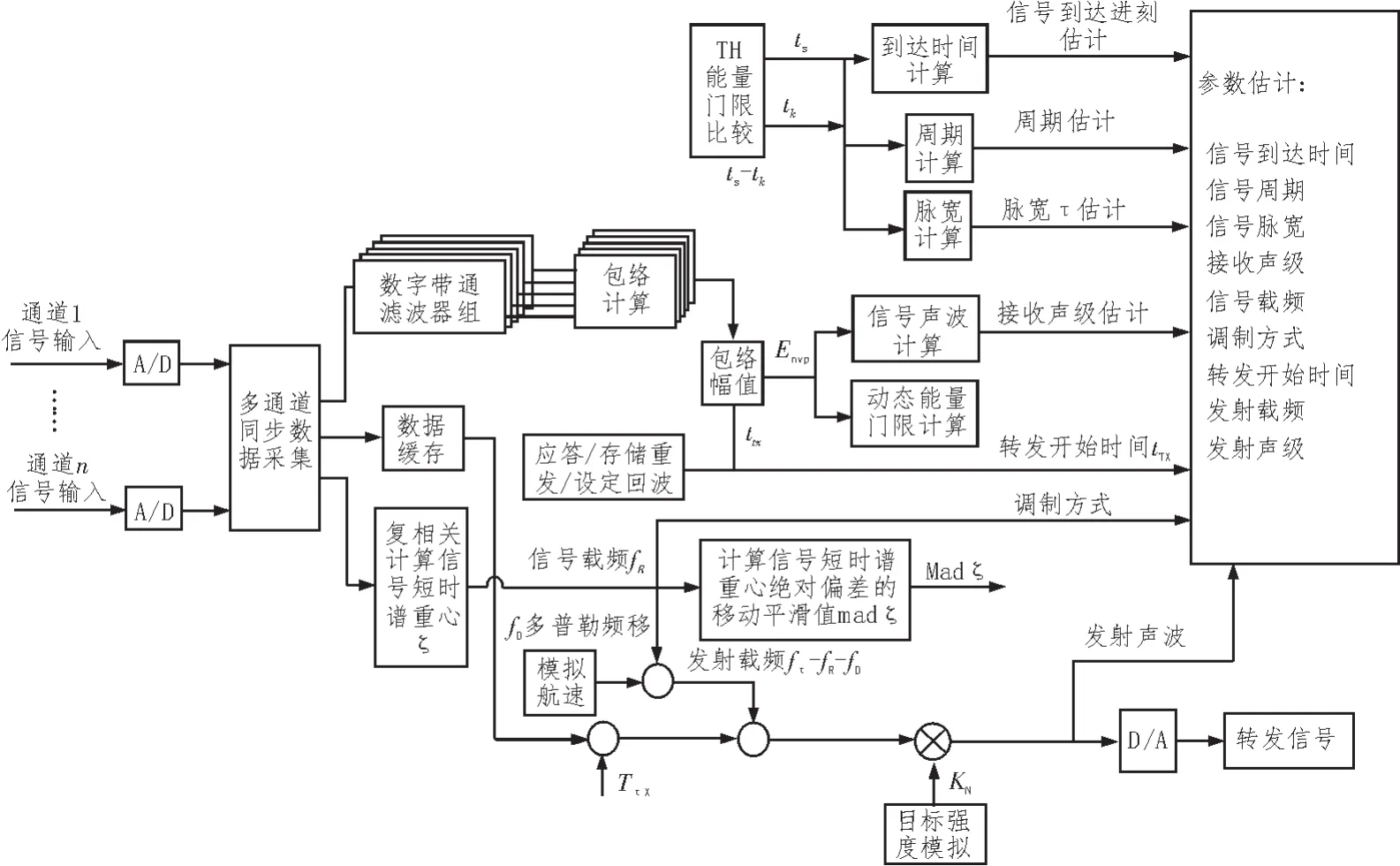
图5 多频信号频率等估计流程图

在脉冲信号的形式未知，信号频率等参数亦未知条件下对整个信号进行观察[16]，首先应对信号的到达时刻进行估计。对通过数字带通滤波器组的信号求包络幅值并与动态能量门限比较，即可以得到检测信号窗口，进而估计出信号到达、结束的时刻。根据信号到达及结束时刻和相邻两个脉冲的信号到达时刻，可以得到信号的脉宽和周期的估计值，根据接收信号包络幅值可以计算出接收声级。其信号检测流程及信号参数估计的流程如图4、图5所示。

4 实验验证

为了验证信号处理算法的可行性，对典型的单频（1个）和多频（4个）脉冲信号进行了实验验证，如图6至图9所示，图中上为接收信号波形和接收信号频谱，下为接收信号在不同频率的信号声级结果。

其中图6为信号脉宽为2 ms，频率为18 kHz时接收信号波形图。图7为信号脉宽为20 ms，频率为18 kHz时接收信号波形图。图8为模拟4个不同频率，脉宽10 ms，幅度较小的的脉冲信号检测试验结果。图9为模拟4个不同频率，脉宽10 ms，幅度较大的脉冲信号检测试验结果。以上试验结果充分证明了该算法的有效性。

图6 2ms脉宽的单频脉冲信号检测结果

5 结束语

在水声多频脉冲信号检测与估计的算法设计中，通过采用三级CIC滤波器实现对多个频点信号的前、后沿的快速检测，以及采用传统的能量检测[17]和madζ法联合检测的方法实现了信号频率等参数的准确估计。实验验证该算法满足在复杂背景噪声下，可靠地检测多频水声脉冲信号；并且还能够对信号的到达时间、载波频率、调制方式、信号脉宽、包络形式或发射周期等做出估计。数据处理算法的有效性得到了验证。

图7 20ms脉宽的单频脉冲信号检测结果

图8 幅度较小的多频点（4个）脉冲信号检测结果

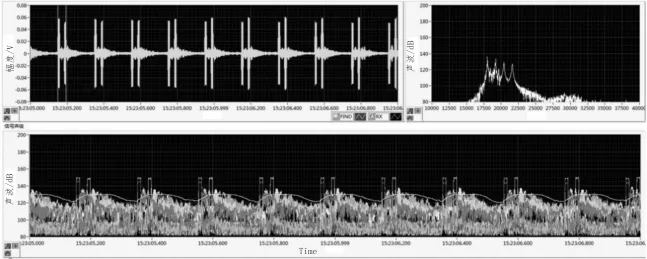
图9 幅度较小的多频点（4个）脉冲信号检测结果

[1]Urick R J，Principle of Underwater Sound 3rd Editon[M].LasAltos，California:Peninsula Publishing，1996.

[2]李强，吴顺君.级联积分梳状滤波器与DSP的实现[J].无线电通信技术，2005，31（3）：21-22，25.

[3]皇甫文斌，朱江，王世练.改进的高性能CIC抗混叠滤波器[J].通信技术，2012，45（7）：119-121.

[4]齐晓辉，王峰，等.多通道中频采样数字下变频应用技术研究 [J].科学技术与工程，2013，13（3）：1821-1826.

[5]史毅俊，朱杰.CIC滤波器的优化设计及FPGA实现[J].电子测量技术，2007，30（3）:88-90.

[6]许彦辉，年夫顺，等.基于FPGA的CIC滤波器优化设计与实现 [J].数据采集与处理，2010，25（S）: 169-173.

[7]牛大胜，唐丽萍.积分梳状滤波器在FPGA中的实现[J].国外电子测量技术，2006，25（9）:48-50.

[8]冯维婷.多速率采样中的CIC滤波器设计与分析[J].现代电子技术，2007（14）:18-20.

[9]刘凌，胡永生.数字信号处理的FPGA实现[M].北京:清华大学出版社，2002.

[10]向大威，许伟杰，景永刚.水声脉冲信号检测的新方法[J].声学技术，2012，31（1）:19-23.

[11]赵树杰，赵建勋.信号检测与估计理论[M].北京:清华大学出版社，2005.

[12]彭鹏菲，邢军，等.一种多通道联合自适应水声瞬态信号检测方法[J].武汉理工大学学报：交通科学与工程版，2010，34（3）:625-628.

[13]McDonough R N,Whalen A D.Detection of signal in noise 2nd edition[M].San Diego:Academic Press，1995.

[14]郑兆宁，向大威.水声信号被动检测与参数估计理论[M].北京:科学出版社，1983.

[15]Miller K S，Rochwarger M M.A Covariance approach to spectral moment estimation[J].IEEE Trans.on IT，1972，IT-18（5）:588-596.

[16]马保科，常红芳，尹纪欣.电磁脉冲信号电离层传播的时间特性[J].西安工程大学学报，2016，30（6）：854-860.

[17]郭红.一类Kirchhoff方程最小能量变号解的存在性[J].纺织高校基础科学学报，2016，29（2）：135-140.

The detection and estimation for multi-frequency pulse signals based on CIC filter& madζ method

SUN Xin，ZHANG Shi-hai
（Navy Forces 91439，PLA，Dalian 116041，China）

In the algorithm of detection and estimation for multi-frequency pulse signals，the fast detection for multi-frequency pulse signals are achievedby using the three-stage CIC filters.A joint detection method using the traditional energy detection and madζ method is used in the exact estimation for the signal parameters，such as signal frequency etc.The processing results from trial data show that the algorithm could effectively detect the underwater acoustics multi-frequency pulse signals in the complicated background noises，the validity of the proposed algorithm is verified.

detection；estimation；CIC filter；madζ method；multi-frequency pulsesignals

TN929.3

：A

：1674-6236（2017）08-0055-06

2016-03-30稿件编号：201603410

孙 昕（1972—），男，黑龙江哈尔滨人，硕士，高级工程师。研究方向：水声测控技术。