基于状态估计和特征模型的高空飞艇定点控制

沈少萍

（厦门大学 航空航天学院，福建 厦门 361005）

基于状态估计和特征模型的高空飞艇定点控制

沈少萍

（厦门大学 航空航天学院，福建 厦门 361005）

针对风场干扰下高空飞艇的定点驻留控制问题，阐述如何利用系统状态估计值和特征模型对飞艇进行控制器设计。首先，在平流层飞艇受力分析的基础上，建立了数学模型；然后设计了扩展卡尔曼滤波器，利用测量得到的飞艇位置信息估算飞艇当前的位置、艇速和风速3个状态变量；随后建立系统特征模型，并将估计所得的状态变量和基于特征模型的黄金分割控制器相结合，对飞艇进行定点控制；最后通过数学仿真验证本文所设计的控制器的有效性，并且和传统PD控制器的控制结果对比，表明了该控制器的优越性。

特征模型；高空飞艇；定点控制；扩展卡尔曼滤波器；状态估计

高空飞艇是重要的浮空平台。它可以携带大量有效载荷长期驻留于20 km左右的高空，在通信中继，对地遥感遥测，空中交通管制等领域发挥类似人造地球卫星的作用。与卫星相比，高空飞艇的机动范围不受轨道限制，驻留范围更广，也容易实现更高的观测精度，还具有可重复使用，节能环保的优点[1-2]。目前，美、俄、加、德、英、法、意、日、韩、以色列等和我国，都在加紧高空飞艇的研究[3-14]。飞艇到达指定位置后，如果没有外部干扰，则无须控制作用就可以静浮于此位置。但实际上，由于种种因素的影响，例如风干扰，往往会使飞艇偏离指定位置，此时需要施加控制作用，定点控制问题就是使飞艇的运动范围不超过完成任务所要求的指标。梁栋等[15]采用李雅普诺夫稳定性理论对平流层飞艇定点保持模式的非线性系统设计了一种非线性控制律，但该控制律对系统模型非常依赖；王延等[16]设计了一种改进遗传算法进行平流层飞艇定点悬停控制，算法复杂且没考虑风场影响；屈卫东[17]采用反馈控制律和状态观测器设计了某飞艇的定点控制律，进行了飞行试验，但控制精度不是很理想；高伟等[18]采用神经网络动态逆控制设计飞艇水平面内的定点控制律并进行仿真，但并没有考虑高空风场模型。

文中利用GPS测量所得的飞艇的实时位置信息设计扩展卡尔曼滤波器（EKF）估计出当前的风速、飞艇位移及飞艇速度，将估计所得的这些状态变量信息与特征模型控制方法相结合对风场干扰下的高空飞艇进行定点控制。在数学仿真中将该控制器的控制结果和传统PD控制器的控制结果想比较，显示出了本文所设计的控制器的有效性和优越性。

1 特征模型理论

特征建模理论[19]和方法是对现有控制理论关于对象建模理论的一个发展，为高阶、参数未知对象进行低阶控制器、自适应控制器和智能控制器的设计提供了理论依据，为工程设计带来极大的方便。基于特征模型的自适应控制方法与常用的间接自适应方法相比，待辨的参数更少，控制器算法更简单。基于特征模型的自适应控制方法在结构上包含了特征建模、特征模型参数辨识、黄金分割控制、逻辑微分等部分。

2 高空飞艇模型

对以定点驻留为目标的飞艇，其基本飞行方式是顶风或顺风飞行，可以简化为质心的一维运动[20-21]。文中针对上述情况建立了高空飞艇的一维运动模型，考虑高空飞艇的水平定点保持。假设飞艇采用硬式多气囊结构。运行过程中，飞艇侧翼推进系统与垂直尾翼协调作用产生侧向力矩平衡侧滑力矩，保证飞艇头部始终逆（顺）着风向[22]；同时水平面推进系统提供动力以平衡风的阻力以及风速变化产生的附加质量惯性力。此时飞艇的运动可以简化为一维运动，受力分析如图1所示，其中T是飞艇的动力，R是风力，而Ra是风速变化产生的附加质量惯性力。

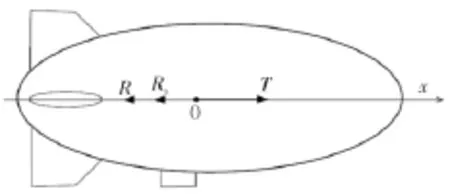
图1 飞艇水平面内受力分析

假设飞艇质量为m，飞艇的位置和对地速度分别为x和vg，由牛顿第二定律，飞艇质心水平运动学方程为

风力和附加质量惯性力满足

其中，vw，ρ，Cx和S分别是风速，大气密度，气动系数和飞艇参考面积。m0是飞艇附加质量，计算公式为[23]

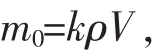
其中V是飞艇体积，k是惯性因子。

假设平流层风场由定常风和阵风组成，风速是定常风速va和阵风风速ω（t）的叠加[24]

假设ω（t）是有色噪声，由零均值白噪声η（t）～N（0，Q）通过成形滤波器生成[25]

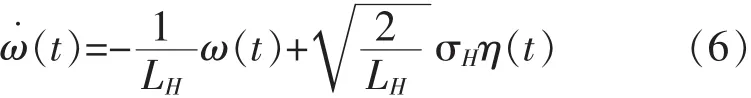
其中LH是水平风速纵向积分尺度，是风速方差，

其中为测量误差，假设d（t）～N（0，R），式（12）是系统的输出方程。

3 基于EKF的飞艇位置、飞艇速度及风速估计

文中设计了扩展卡尔曼滤波器（EKF），提出用飞艇的位置信息估算飞艇的实时位置、艇速和风速。飞艇的位置可以通过GPS或地面测量得到，但存在测量误差。

EKF是非线性系统滤波的有效方法[25-26]。考虑上述非线性系统

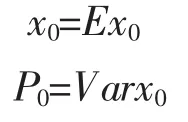
利用扩展滤波公式（17）和（18），在给定初始条件下进行迭代运算就可以估计状态x。

4 高空飞艇水平面定点控制律设计

1）状态估计值和特征模型方法相结合的自适应控制方案设计

①特征建模

根据文献[19]，可对系统状态方程式（11）、（12）进行特征建模，得：

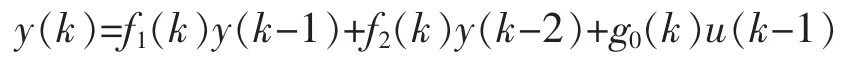
②黄金分割自适应控制律

③逻辑微分控制律:

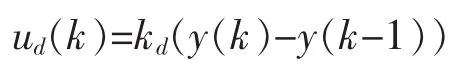
其中kd为可调逻辑参数。

将状态估计值和上述黄金分割控制律和逻辑微分控制律相结合得到总的控制量为

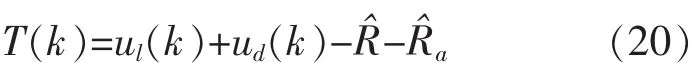
图2 基于特征模型控制器的飞艇定点保持闭环受控系统

5 数学仿真研究

设飞艇初始位置为离原点5 km处，需要定点到原点位置并保持，受风场扰动影响，平流层风场由定常风和阵风组成，定常风设为-10 m/s，叠加阵风风速ω（t），飞艇位移可由GPS测量得到，通过EKF算法得到飞艇位移，飞艇速度和风速的估计值，这些状态变量的估计值及其跟真实值的偏差如图3～图5所示，并比较传统PD控制方法和本文设计的控制方法的控制效果，如图6所示。从图3可以看出，300 s后飞艇位移的估计值的误差为±1 m以内，飞艇速度估计误差在±0.05 m以内，对风速的估计误差在±0.2 m内，这些数据表明用EKF估计系统状态变量是有效的。图6中，用本文设计的特征模型和状态变量估计相结合的控制方法将飞艇定点到原点位置，400 s后定点误差在±1 m以内，但若采用传统的PD控制，控制结果存在一个平均-6 m的偏差量，所以数学仿真表明了本文设计的控制方法的有效性和优越性。

图3 采用EKF对飞艇位移的估计及估计误差曲线

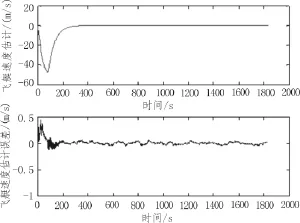
图4 采用EKF对飞艇速度的估计及估计误差曲线

图5 采用EKF对风速的估计及估计误差曲线

图6 采用传统PD控制和采用特征模型控制的飞艇位移定点误差对比曲线

6 结 论

文中基于高空飞艇的一维运动模型设计了扩展卡尔曼滤波器（EKF），估计出了飞艇位移、飞艇速度和风速，并将估计所得的这些状态变量信息和基于特征模型的黄金分割控制相结合对飞艇进行定点驻留控制，数值仿真表明，EKF估计风速在风速包含有色噪声时具有良好的精度，所设计的控制方法能够有效用于风场干扰下的高空飞艇定点驻留控制，为进一步研究高空飞艇的风速估计和进行飞艇高精度定点驻留控制打下了基础。

[1]李智斌，吴雷，张景瑞，等.平流层飞艇动力学与控制研究进展[J].力学进展，2012，42（4）:482-493.

[2]樊昌信.一种发展中的新移动通信方式-平流层通信研发概况[J].现代电子技术，2005，210（19）:1-3.

[3]Stavros P.Androulakakis，Ricky A.Judy，Status and Plans of High Altitude Airship（HAATM）Program [C]//Aerodynamic Decelerator System Technology Conferences，AIAA Lighter-Than-Air Systems Technology （LTA）Conference，25-28 March 2013，Daytona Beach，Florida，USA.

[4]Neydorf Rudolf，Sigida Youriy，Voloshin Vitaly，Chen Yong.Stability analysis of the MAAT feeder airship during ascent and descent with wind disturbances[C]//SAE 2013 Aero Congress and Exhibition，AEROTECH 2013，September 24-26，2013.

[5]Grumondz VT，Stability of the stationary motion of the airship[J].Russian Aeronautics，2016，59（1）: 29-35.

[6]Kwon Ji-Wook，Kim Jin Hyo，Seo Jiwon.Vector field guided auto-landing control of airship with wind disturbance[C]//19th IFAC World Congress on International Federation of Automatic Control，IFAC 2014，August 24-29，2014.

[7]Kazuhisa Chiba，Shin Satori，Ryuichi Mitsuhashi，etc， Behavior of tether for captive stratosphere platform using airship[C]//Asia-Pacific International Symposium on Aerospace Technology，APISAT 2014：24-26.

[8]Alessandro Ceruti，Pier Marzocca，Conceptual approach to unconventional airship design and synthesis[J].Journal of Aerospace Engineering，2014，27（6）:4014035.

[9]Jelenciak Frantisek，Gerke Michael，Masar Ivan. Airship aerodynamics-Modeling principle of the aerodynamic forces by PEM method [C]//Proceedings of the 2013 International Conference on Process Control，2013:25-30.

[10]Kahale Elie，Garcia， Pedro Castillo， Bestaoui Yasmina.Autonomous path tracking of a kinematic airship in presence of unknown gust[J].Journal of Intelligent and Robotic Systems:Theory and Applications，2013，69（1-4）:431-446.

[11]Bennaceur Selima，Azouz Naoufel.Contribution of the added masses in the dynamic modelling of flexible airships[J].Nonlinear Dynamics，2012，67（1）:215-226.

[12]Wu Jiangtao，Fang Xiande，Wang Zhenguo，et al. Thermal modeling of stratospheric airships[J]. Progress in Aerospace Sciences，2015，75:26-37.

[13]Dai Qiumin，Fang Xiande.Numerical study of forced convective heat transfer around airships[J]. Advances in Space Research，2016，57（3）:776-781.

[14]Han Ding，Wang Xiaoliang， Chen L.I.，et al. Adaptive backstepping control for a multi-vectored thrust stratospheric airship with thrust saturation in wind [J].Proceedings of the Institution of Mechanical Engineers， Part G: Journal of Aerospace Engineering，2016，230（1）:45-59.

[15]梁栋，李勇.平流层飞艇定点保持模式控制方法研究[J].航天控制，2008.8，26（4）:35-39.

[16]王延，周凤岐，周军，郭建国.基于改进遗传算法的平流层飞艇定点悬停控制 [J]，火力与指挥控制，2010，35（2）:22-27.

[17]屈卫东，范启富.平流层演示飞艇自主飞行试验[J].装备指挥技术学院学报，2007.2，18（1）:96-98.

[18]高伟，王生，姜鲁华.基于神经网络动态逆的飞艇定点控制及仿真[J].微计算机信息，2010，26（5-1）: 56-57.

[19]吴宏鑫，刘一武，刘忠汉，等.特征建模与挠性结构的控制[J].中国科学（E辑），2001，431（2）:137-149.

[20]Lin X，Hong L，Lan W.One dimensional trajectory optimization for stratospheric airship with varying thruster efficiency[C]//2013 10th IEEE International Conference on.IEEE，2013:378-383.

[21]Hong L，Lin X，Lan W.Mode switch sequence analysis on one-dimensional trajectory optimization of stratospheric airships[J].Control and Intelligent Systems，2014，42（2）:151-158.

[22]方存光，王伟.自主飞艇水平位移动力学建模及其控制[J].控制理论与应用，2007，24（2）:161-169.

[23]（俄）尼卡拉伊维奇.现代飞艇设计导论 [M].吴飞，王培美，译.北京:国防工业出版社，2009.

[24]Nichita C，Luca D，Dakyo B，et al.Large band simulation of the wind speed for real time wind turbine simulators [J].IEEE Trans.Energy Conversion，2002，17（4）:523-529.

[25]徐明友，丁松滨.飞行动力学[M].北京:科学出版社，2003.

[26]秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理[M].2版.西安:西北工业大学出版社，2012.

Fixed point control of high altitude airship based on state estimations and the characteristic model

SHEN Shao-ping
（School of Aerospace Engineering，Xiamen University，Xiamen 361005，China）

To solve the problem of the fixed point control of high altitude airship disturbed by the wind field，the design of a controller based on the system state estimation and the characteristic model is presented.First，the mathematical model is established based on the force analysis of the stratospheric airship，and then designed the extended Kalman filter，using the measured location information of the airship to estimate the airship current position，airship speed and wind speed.Then the system characteristic model is established，and the estimated state variables are combined with the golden section controller based on the characteristic model.Finally，the effectiveness of the proposed controller is verified by mathematical simulation，and compared with the control results of the traditional PD controller，the superiority of the proposed controller is demonstrated.

characteristic model；high altitude airship；fixed point control；extended Kalman filter；state estimation

TN710

：A

：1674-6236（2017）08-0001-05

2016-07-28稿件编号：201607199

国家自然科学基金面上项目（61273199）

沈少萍（1978—），女，福建厦门人，博士，助理教授。研究方向:控制理论及其航空航天应用。