大规模风电接入对电力系统暂态稳定性影响研究综述
林旻威 温步瀛
大规模风电接入对电力系统暂态稳定性影响研究综述
林旻威温步瀛
(福州大学电气工程与自动化学院,福州350108)
近年来随着风电装机在电力系统中的比例逐步增加,风电场并网对电力系统的影响越来越大。本文总结了从风力发电机单机建模、风电场聚合建模到含风场的系统暂稳特性等相关技术研究成果,并对含风电电力系统的暂态特性分析方法进行了概括分析,比较了各种方法的优缺点。最后,对相关技术的发展趋势做出预测,提出了一些后续研究的建议。
风力发电;变速恒频;机电暂态稳定性;时域仿真;直接法
我国从20世纪50年代开始探索发电技术,80年代中期引入了55kW容量等级的风力发电机组,并将其投入了商业应用。在此之后的近30年内,世界范围内的风力发电机组均向大容量、高参数发展,我国的风力发电产业也已基本成熟。受到金融危机的影响,我国风电新增装机容量在2008—2009年有小幅度的下降,近几年来我国的风电装机仍然进展迅猛,2009—2015年年均风电新增装机也达到了1905万kW。到2015年为止,我国的风力发电装机总容量已经达到了14536万kW[1-2]。
随着并网运行的风力发电穿透率日渐提升,对风力发电的研究重点逐渐从风力发电机的电能质量转移到了由并网风机所引起的电网运行稳定性问题上[3]。由于各类风力发电机组的工作原理和连接方式与传统的同步发电机组均有较大的差异,以前的稳定性研究方法和研究工具在并网风机的稳定性问题上难以适用。电力系统电磁暂态与机电暂态的仿真是研究该问题的重要手段,而对风力发电机组的准确建模是该研究方法有效的重要保证[4]。
本文从不同的角度,对国内外在大规模风电并网影响电力系统暂态稳定性方面的各研究成果进行了总结,为后续的研究提供了思路和启发。
1 风电机组及其控制策略的建模
1.1 风速及风力机建模
风力机是风力发电机组的原动机,工作时捕获风中的动能并将其转化为机械能。许多文献都从贝兹理论[5-10]出发,建立了风速、风力机转速与风力机转轴上的输出功率与输出力矩的关系,如式(1)、式(2)所示,并可以据此画出不同风速下风力机的输出功率与风力机转速的关系,如图1所示。
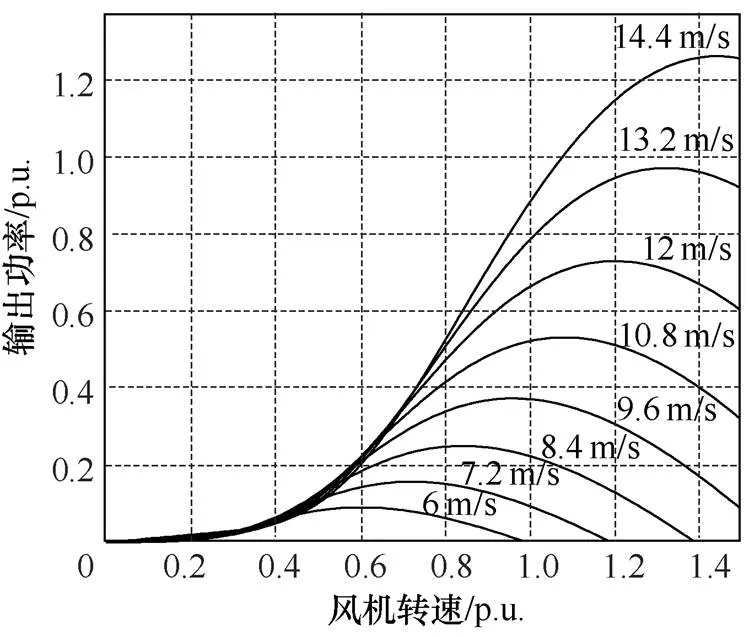
图1 不同风速下风力机的输出功率特性
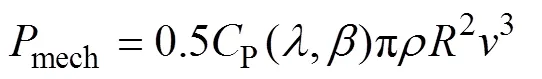
(2)
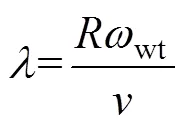
在对风速的建模中,根据不同的应用场景,有的文献将风速看做恒定值,有的文献采用了四分量法[7]对短时间内的风速变化情况进行了模拟。文献[6]将时间序列法应用于风速与风力发电功率的预测,引入了Weibull分布对时间序列法预测得到的风速序列进行了修正,并与时序神经网络法风速预测进行对比。文献[11]则使用了时间序列法得出了一种适合于风力发电机组暂态特性仿真的风速模型。
1.2 传动轴模型
传动轴在风电机组中用于传递风力机的输出功率。大部分文献中均采用了双集中质量块法[4-12]来描述传动轴的弹性动态。除此之外,还有一些别的传动机构的数学模型,例如文献[12]中提到的三质量块等效模型及单质量块等效模型,以及文献[13]提到的基于行星齿轮机构的风电齿轮箱模型。文献[14]提出了一种可以借助发电机功率控制来调整风力机偏航方向的风力发电机组传动机构模型,但是该机构及其控制过于复杂,不便于大规模应用。
1.3 双馈风力发电机建模
双馈风力发电机组(DFIG)是一种已经被广泛应用的变速恒频风力发电机型,其系统结构如图2所示。
与其他的风力发电机组的机型相比,双馈风力发电机有许多优点,例如双馈风力发电机组中的电力电子变流器只需要对转子的功率进行变换与处理,大大减小了所需要的变流器容量;还可以通过对转子侧变流器的控制实现双馈发电机定子的有功、无功解耦控制,在运行上具有很大的灵活性[3]。文献[10-15]均给出了双馈发电机的5阶模型与3阶模型,并通过仿真手段比较了两个模型的区别。3阶模型与5阶模型相比,略去了定子磁链的变化动态,因此模型更加简洁。式(4)为DFIG的5阶矢量表示的数学模型。
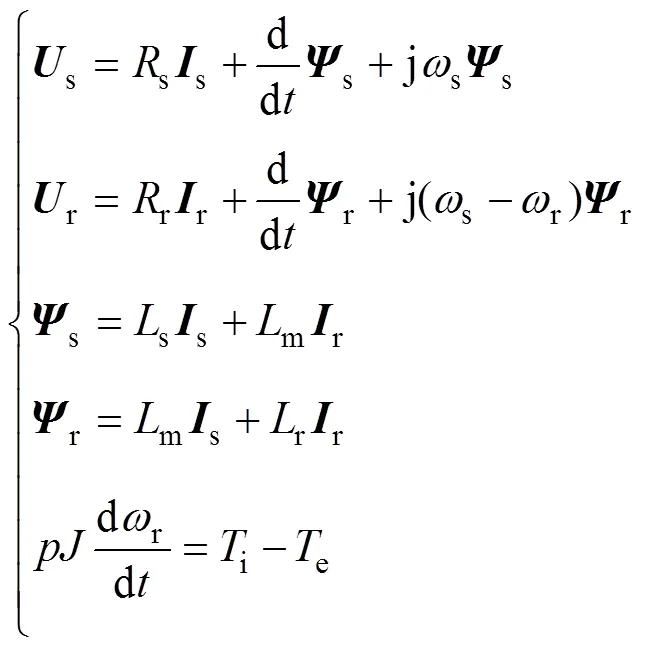
在仿真计算中,一方面与5阶模型的差别并不明显,另一方面可以省去较多的计算时间,且在电力系统机电暂态仿真计算中,3阶模型可以更好地与电力系统的网络模型对接。文献[16]在双馈发电机的5阶模型基础上使用定子磁链跟踪同步旋转坐标系提出了双馈发电机的直接功率控制方法;文献[17]在文献[16]的基础上实现了电网电压不对称情况下的双馈发电机直接功率控制。文献[9]利用AMPSO算法,先通过试测法得到了双馈电机对扰动的响应曲线,再使用基于AMPSO算法的电机模型参数辨识方法建立了双馈电机的等值模型,最后通过仿真证实了该模型的有效性。
1.4 永磁同步风力发电机建模
永磁同步风力发电机(PMSG)是一种以多极永磁同步电机作为发电机,并将全部发电功率通过电力电子变流器变换为工频电能馈入电网的一种新型变速恒频风力发电机,系统基本结构如图3所示。
PMSG风电机组的数学模型为

文献[5,18-19]等详细介绍了多极永磁同步电机的结构与工作原理,并且给出了多极永磁同步电机的数学模型,如式(5)所示。文献[20]介绍了一种采用了双星形定子绕组的多极永磁同步电机,并给出了其数学模型和d、q轴解耦控制方法。背靠背连接的三相电压源型变流器是永磁同步风力发电机组中的一个重要部分,文献[21]给出了电机侧及电网侧的电力电子变流器的数学模型。零d轴电流是一种最常用的永磁同步电机控制方法,文献[5-22]阐述了电机侧变流器的零d轴电流控制方法,并指出该控制方法的优点在于可以实现电流大小与转矩的线性关系,以及能够保护永磁体,使其不被电机定子上的去磁电流退磁等。
2 风电场等值
目前的大多数风电场经常由几十台甚至上百台风力发电机组成,集中并网发电。在实际的仿真运算中,如果对风电场中的每一台机组均进行详细地建模与计算,将会导致过长的计算时间消耗和过度的内存使用。为了解决这个问题,需要对风电场建立动态的等值模型,来减少仿真计算时的计算资源消耗[23-24]。风电场等值有多种不同的等值方法,针对采用了不同机型的风电场,在搭建等值模型时也有很多不同之处。
风电场中的风机分群是风电场等值的重要的一环。文献[25-29]指出,分群的前提是群内的机组同调,常用的信息源包括风电机组的初始运行状态、状态量在受扰初始时刻的数据及受扰过程中的事件响应数据等。文献[29-31]均采用了聚类分析的方法来搜索风电场内的同调风电机组,区别主要在于分群指标的选取,其中文献[29]选取的是风力发电机组在故障发生后的几个时间点的转速,而文献[30]选取的是各风力发电机组在风电场PCC发生三相短路故障后的机端电压动态轨迹作为分群的依据。文献[32]基于风电场功率曲线,提出一种作用于等值风力机模型上的等值集合风速模型,这能够解决由于风电场内各风机所受风速不同而产生的等值困难的问题。
文献[25]总结了几种针对采用了笼型异步发电机的风电场等值方法,分别为容量加权单机等值方法、改进加权单机等值方法、参数变换单机等值方法和变尺度降阶多机等值方法,其中参数变换单机等值方法适用于采用了多种不同型号的风力发电机组的风电场;变尺度降阶法一般用于风电机组参数一致且排列规则的风电场,这种方法考虑了尾流效应和风机运行点的不同。文中在对风速尾流效应的建模方面选择了Jensen尾流效应模型。随着新型的变速恒频风力发电机组的普及,针对笼型异步风电场的等值方法的应用场合将会变少,但是针对尾流效应的Jensen模型仍然可以应用于变速恒频风电场中的尾流效应仿真中。
随着风力发电技术的迅速发展,双馈笼型风电场的装机量显著增大,且在海上风电领域的应用前景十分广泛。双馈笼型风电场采用了具有变速恒频运行性能的双馈风力发电机组,与笼型异步风电场相比,其运行的灵活性有很大的改善,动、暂态特性也与笼型异步风电场有所区别。文献[33]提出了基于双馈风电机组参数聚合的风电场等效方法;文献[34]在考虑双馈风电机组分群的前提下,针对同群机组采用了参数聚合方法进行了等效建模;文 献[35]考虑风速波动和风电场内集电网络构架,基于分群的参数聚合方法建立了整个双馈风电场的等值模型。实际投运的双馈风电机组均带有Crowbar保护电路,该电路是双馈风电场实现故障穿越的关键。文献[36]考虑双馈风电机组的Crowbar电路,选择Crowbar电路的投入时间与电阻值,建立了考虑Crowbar动作特性的双馈机组风电场等效模型。
永磁同步风力发电机组也是一类重要的变速恒频风力发电机组。与双馈风电机组相比,永磁同步风电机组的控制回路少,控制比较简单;永磁同步风电机组的并网采用电压源型交直交变频器,容量达到了永磁同步电机额定容量的1.2~1.4倍,在实现柔性并网的同时产生了较大的成本;相同容量的永磁同步风电机组的装机成本大于双馈风电机组[37]。文献[38]根据基于风电场出力计算的等值风速曲线,采用参数聚合法,建立了考虑风电场内部集电线路参数的永磁同步风电场等值模型。文献[39]采用单台风电机组模型与理想受控电流源结合的方式,建立了永磁直驱风电场的聚合模型。
风电场等值的目的是避免计算机在对风电场仿真时需要对场内每台风电机组逐一建模仿真,防止仿真模型“维数灾”的出现。在目前的研究中,针对该问题的研究思路主要有两种:①在已知风电场所采用风电机组型式的前提下,根据风电场的外特性,采用单机或多机等值方法来得出风电场的等效模型,并使用一些智能算法找出风电场等效模型的参数;②通过详细分析风电场内的各风电机组运行状况以及结线方式,在根据机组的运行状况合理分群后,运用合理的等值方法,得出该风电场聚合模型的各个参数。总而言之,风电场的等值,也即风电场聚合建模,主要的目的是平衡风电场仿真计算量与仿真精度。采用较精确复杂的建模方案,就会带来模型阶数过高、计算资源占用过大等问题;采用简单的单机等值等方法,就有可能出现仿真精度不符合要求等问题。
3 风电场的机电暂态特性与含风电电力系统的暂态稳定性研究
3.1 含风电电力系统的暂态稳定性分析的必要性
在大容量风电并网运行的情况下,由于风电出力的不确定性,电网的运行特性将会十分复杂,电网的安全形势也与风电大规模并网前的传统电力系统有较大区别。将并网运行的风电场计入电力系统的动态安全分析,有助于电网调度部门更好地安排输电计划、更好地对风电场及常规同步机组进行调度,在保证安全水平的前提下提高输电线路的利用率。因此在当前风电大规模并网的背景下,研究含大规模风电场的电力系统的暂态稳定性对电力系统的运行安全具有重要意义[40]。
3.2 风电场的机电暂态模型
不同于传统的同步发电机组,双馈风电机组与永磁直驱风电机组都是变速恒频机组,它们的出力与转速解耦,不能提供与传统同步发电机的电力系统惯量。因此,变速恒频风电场的暂态稳定特性与传统的同步发电机组有较大的区别。在对含有大规模风电的电力系统进行动态安全分析时,需要将不同于传统同步发电机模型的新型风电场的机电暂态模型引入电力系统的动态安全分析中[33-41]。由于详细的风电机组电磁暂态模型模型考虑了风力发电机定子磁链的动态以及电力电子变换器的动态特性等,在实际工程中使用时存在模型过于复杂、计算时间长等问题。因此必须开发一个由风电机组电磁暂态模型简化而来的机电暂态模型,才能满足电力系统机电暂态仿真的要求[42]。文献[41]基于异步电机三阶模型,在考虑转子侧变流器的控制策略与Crowbar保护的动作特性的前提下建立了适用于机电暂态仿真的双馈风电机组模型。文献[42]在PSASP与PSCAD两种仿真环境下测试了简化的双馈风电机组机电暂态模型。文中所介绍的模型与详细的电磁暂态模型能够较精确地吻合,在保证计算精度的前提下大大减少了计算时间。
机电暂态模型与电磁暂态模型之间最大的区别在于,机电暂态模型仅需计及仿真对象的电磁转矩、转速等运行数据的动态,而对于电气量均采用准稳态的模型来表示。这样做的优点在于,风电场模型与电气网络之间的配合更加简单,而且能够合理地规避暂态下由电磁暂态造成的电磁转矩波动等问题,使仿真计算更加简洁。由于采用不同机型的风电场并网方式不同,其机电暂态模型也有较大的差异。以双馈风电场与永磁直驱风电场为例,双馈风电场的定子直接并网,转子则通过励磁变频器作交流励磁运行,故在建立机电暂态模型时可以参照同步发电机的机电暂态模型,使用电机的暂态电抗,以及在机电暂态过程中不变的暂态电势来表示场内风电机组在机电暂态过程中的动态。但是这种建模方法没有考虑双馈发电机组与同步发电机组之间的差异,特别是机组结构和其分别对应的励磁系统之间的差异。这样就有可能导致仿真结果不够精确。也有部分模型采用了DFIG 3阶动态方程,并考虑其运行控制系统,也即其励磁系统,形成完整的DFIG机电暂态模型,进而推导出双馈风电场的机电暂态模型。这种模型虽然能够提供精度很高的仿真结果,但是不论DFIG发电机组本身还是其控制系统,都含有较多的状态变量,造成整个模型阶数过高,不利于仿真计算的运行。现在比较常用的双馈风电场模型,多为注入电流源模型、功率注入模型与恒阻抗模型等,例如文献[42]所提出的“电流源-电压源-无源阻性”三状态切换模型。这类简单的模型在暂态中可以大致地代表双馈风电场自身的机电暂态特性以及其对电力系统的影响,但是精确度并不高,因此常用于定性的直接法研究。永磁直驱型风电场的并网方式比较简单,其所有功率均通过一个交直交变频器变换成工频的电能后,注入电网,因此其机电暂态特性主要体现为永磁直驱机组中并网变换器的暂态特性。并网变换器的运行控制十分灵活,在机电暂态仿真计算中可以看作网侧变换器滤波电抗后面的受控电压源。因此其机电暂态特性可以等效为网侧变换器的功率注入特性,主要受到网侧变换器控制系统动态特性的影响。
综上所述,在建立风电场的机电暂态模型时首先要考虑场内装机的机型,再结合一些等值建模方法,才能最终得出合理的结果。
3.3 含大规模风电电力系统的暂态稳定性分析
电力系统暂态稳定性分析的技术已经相当成熟,主要的方法有时域仿真法与暂态能量函数法(EEAC)[42-43]。一般而言,时域仿真法的适应性比较强,物理意义明确,可以根据仿真计算得出的轨迹准确地判断电力系统在某个故障发生时的暂态稳定性,但是时域仿真法无法给出稳定性的定量指标。直接法通常有暂态能量函数法和扩展等面积准则法等,优点在于计算速度快、可以给出稳定裕度,但是这种方法对模型的适应性不够好。实践证明,直接法与时域仿真法互补性强,无法互相取代。将两种方法相结合既能增强模型的适应性、得到精确的仿真轨迹,又可以计算出各种稳定性指标。
在目前的研究中,一部分文献[44-47]采用了时域仿真的方法来研究含风电电力系统的暂态稳定性。文献[44]认为风场并网后的电力系统暂态稳定性与并网点、故障位置均相关,与同容量的同步机组相比可能使系统的暂态稳定性变好,也可能变差,不能一概而论。文献[45]通过仿真研究了大风电比例送端电网的暂态稳定性,文献[46]定义了双馈电机的功角,阐述了双馈风电机组对电力系统暂态稳定性影响的机理。这部分文献得到的结论基本一致,即认为新型的变速恒频风力发电场代替原有的同步发电机组时,可以通过对机组的故障穿越控制,使整个系统的暂态稳定性得到增强。但是没有总结出风场接入对系统暂稳性能影响的普遍规律。
文献[48-55]应用扩展等面积准则,在双机系统中通过研究风机接入导致的功角变化及功角加速度变化,来给出系统在接入风机后的暂态稳定性变化情况,最后通过时域仿真来验证文中所提的暂稳特性变化规律。文献[50]将风场的机械功率及注入有功功率等效成同步发电机组的机械功,并由此推导含风电电力系统的扩展等面积准则。文献[48-49]在系统无功补偿措施充足、风电场并网公共连接点PCC电压波动较小的情况下,采用了双馈风电场功率注入模型,即认为故障后的瞬间风电即可恢复故障发生之前的出力水平,没有波动过程。但是文献[53]认为,在并网功角稳定水平影响研究中,将双馈风力发电系统等效为恒功率源进行分析,较之实际工况是较为保守的。文献[51]认为DFIG风电场在故障恢复之后应当看做恒阻抗功率源,即出力与电压幅值相关。多数文献[50-55]在应用扩展等面积法的时候都采用了系统的交流潮流模型,即功角特性为一个正弦函数,但是文献[48-49]采用了直流潮流模型,即认为系统中传送的功率与功角差成正比。这种模型虽然在系统功角差较大时有较大误差,但是能够在保证定性判断的准确性的前提下降低分析过程的复杂程度,有一定实用价值。
基于传统电力系统暂态稳定分析的直接法及其部分延伸方法在大规模风电接入对电力系统暂稳性能影响的研究方面也有所应用。文献[56]以机电暂态分析中负荷的暂态能量为切入点,提出了风电场端口能量的概念,并将其应用于风电系统的暂态稳定分析中。文献[57]介绍了含风电电力系统失稳模式与系统方程奇异面之间的关系,并指出风电比例的增加会使系统的非线性增强,从而改变系统的失稳模式。另一些研究中[58-59]着重考虑了风电场本身的一些特性,例如文献[58]引入了与风电场装机地理位置相关的风速相关性,文献[59]考虑了风电不确定性对系统暂态稳定性影响,这表明,之前只在宏观的系统调度中考虑的一些因素,现在也被引入到了含风电电力系统的暂态稳定研究中来。
综上所述,含风电电力系统的暂态稳定性与众多因素有关,包括风电穿透率、系统中同步机组的负荷情况、风电场所采用的风电机组型式有关。一般而言,在大规模风电的接入不改变电力系统潮流的情况下,只要风电场本身具有故障时无功补偿的能力,那么风电场的接入是有利于电力系统的暂态稳定的。因此与恒速恒频的鼠笼式风电机组相比,新式的变速恒频机组一般能够使电力系统的稳定性增强,但是风电占比很大的情况仍然有待研究。需要强调的是,若风电的接入改变了系统运行的潮流、同步发电机组的运行状态,那么得出的结论是不具参考价值的。
4 总结与展望
随着风力发电比例的不断增加,在电力系统暂态稳定安全校核方面考虑风电的并网和出力已经不可避免。虽然各类风电场建模方法的研究已经逐步完善,但是如何在暂态稳定仿真计算中通过合理地简化风电场模型,来达到又快又好的仿真效果仍然没有定论。在风力发电机组及风电场建模方面,很多电力系统仿真软件已经开发了内置的动态模型,例如PSASP、PSCAD、DIgSILENTPowerFactory等。但是这些模型只能适用于各自的仿真环境,与其他仿真软件不兼容,通用性不高,且模型的内部结构不够清晰,同条件下各模型之间的仿真结果也有所差异。
本文对含大规模风电电力系统暂态稳定性问题及相应的分析方法进行了综述,总结其内容如下:
在风电场的建模方面,大部分研究都采用了基于风电场所采用风电机组本身的暂态特性的方法,即根据风电机组本身的电磁暂态特性,在采取了简化措施之后,保留与机电暂态的时间尺度比较相关的一部分特性,即可得到适用于机电暂态分析的风力发电机组模型。一些其他研究中,根据风力发电机组的动态模型,进行了机组运行点附近的线性化模态分析,并应用主成分分析方法挑选出机组在机电暂态尺度上的重要暂态特征模态。类似的思路可以应用到风力发电机组暂态模型的建立上。对于整个风电场而言,可采取单机等值方法为风电场建模,也可以依据风电场内风电机组工作状态的不同,可采取不同的方案对场内风电机组进行分群,再进一步采用组合的风电场模型对其进行模拟。应当指出,各类将风电场模型简化处理的方法,都是为了避免仿真计算模型的维数灾而开发的。随着现在电子计算机计算能力的跨越性进化,最终应力求将完整的,包含风电机组精确模型、风电场内集电线路电磁暂态模型的风电场模型应用与电力系统暂态稳定性研究中。
在含风电电力系统暂态分析方面,大部分研究中根据传统的电力系统暂态分析方法,发展出了一些结合时域仿真法和直接法的电力系统稳定分析方法。时域仿真法方面,当前的热点在于电磁-机电混合仿真方法在含风电电力系统暂态特性分析中的应用。电磁-机电混合仿真方法是随着高压直流输电系统的投运而被提出、开发的,其本质是针对仿真对象中特征时间常数的数量级有区别的两个部分进行差异化处理。由于风电机组的多时间尺度特性,可以利用电磁-机电混合暂态仿真方法中的电磁暂态部分,对风电机组中涉及到PWM变换装置、直流母线等环节的部分进行处理,而对系统其余时间常数与机电暂态仿真步长相近的环节应用机电暂态分析方法处理,以达到工程上的精度、效率的平衡。直接法方面,目前采用暂态能量函数法来研究风电大规模并网对电力系统暂态稳定影响的例子还比较少,大多数研究中都运用了扩展等面积准则,以双机摇摆系统为对象来研究风电并网对系统稳定性影响的问题。
由于现有分析理论和手段的种种不足,本文在现有的一些研究成果的基础上提出如下展望:
1)新型风电场等效模型及应用
现代的变速恒频风电场均具有较强的故障穿越、无功补偿、故障时的无功电流注入、正负序电流控制等功能,在系统故障时可以提高公共连接点电压水平,减少有功注入,这都有利于系统的暂态稳定。这使得现有的部分研究成果对风电接入后的电力系统暂态稳定水平的判断不够准确。因此,将新型的风电场机电暂态模型应用于含风电电力系统的暂态稳定仿真校核中,可以获得更加准确的结论。
2)电磁暂态-机电暂态混合仿真方法的应用
现代的大规模风电场多采用大容量变速恒频风力发电机组,其动态特性在很大程度上受到机组控制系统与电力电子变换器特性的制约。由于风电机组的多时间尺度特性,与机电暂态仿真计算中的一些仿真对象(如同步发电机励磁系统、电力系统稳定器的动作情况、功角的摆动等)相比,变速恒频风电机组中的运行控制系统、电力电子变换器等部分的暂态时间常数大大减小,常规机电暂态仿真的时间尺度无法满足其分析需要,需要在风电场部分应用电磁暂态尺度的仿真手段来对其暂态响应过程做更进一步的研究。在这方面,目前已经有SMRT、ADPSS等软件在直流输电系统仿真中得到应用,但是在其对风电场的暂态研究方面还需要继续推进。
3)智能化的暂态稳定分析方法的提出
现有的含风电电力系统暂态稳定分析方法大都是时域仿真法与直接法或暂态能量函数法的结合。这类方法虽然能在给出精确暂态过程仿真轨迹的同时计算出稳定裕度,但还无法对系统的失稳模式做出准确判断。因此,将现有的暂态稳定分析方法与模式识别、神经网络等人工智能方法结合起来,提高暂态稳定分析系统的自动化水平,是下一步研究的一个主题。
4)基于互联网与数据库技术的暂态稳定分析系统的开发
根据大部分研究的结论,大型风电场的运行状态,尤其是出力水平,对系统在故障下的暂态稳定性影响较大。而风电场的运行受到风况、天气状况等多重因素的影响,具有较大的不确定性,对暂态稳定分析系统的实时性与准确性有较大影响。因此,利用互联网和数据库技术,实现含风电电力系统暂稳分析与系统运行数据、系统运行状态监测系统之间的数据链接,可以有效增强暂稳分析系统的实时性与有效性,有较高的研究价值。
[1] 王丽宏. 我国风力发电现状及技术发展[J]. 科技与企业, 2015(18): 96-96.
[2] Polinder H. Basic operation principles and electrical conversion systems of wind turbine[C]//Proceedings of the Nordic workshop on power and industrial elec- tronics, 2004: 43-50.
[3] Lei Y Z, Mullane A, Lightbody G, et al. Modeling of the wind turbine with a doubly fed induction generator for grid integration studies[J]. IEEE Transactions on Energy Conversion, 2006, 21(1): 257-264.
[4] 许寅, 陈颖, 梅生伟. 风力发电机组暂态仿真模型[J]. 电力系统自动化, 2011, 35(9): 100-107.
[5] 赵仁德, 王永军, 张加胜. 直驱式永磁同步风力发电系统最大功率追踪控制[J]. 中国电机工程学报, 2009, 29(27): 106-111.
[6] 肖洋. 风电场风速和发电功率预测研究[D]. 长春: 东北电力大学, 2005.
[7] 韩肖清, 雷巧红, 胡月星, 等. 含风电场的电力系统动态仿真[J]. 太原理工大学学报, 2007, 38(3): 244- 246.
[8] 刘其辉, 贺益康, 赵仁德. 变速恒频风力发电系统最大风能追踪控制[J]. 电力系统自动化, 2003, 27(20): 62-67.
[9] 栗然, 唐凡, 刘英培, 等. 基于自适应变异粒子群算法的双馈风电机组等值建模[J]. 电力系统自动化, 2012, 36(4): 22-27.
[10] 尹明, 李庚银, 周明, 等. 双馈感应风力发电机组动态模型的分析与比较[J]. 电力系统自动化, 2006, 30(13): 22-27.
[11] 李东东, 陈陈. 风力发电系统动态仿真的风速模型[J]. 中国电机工程学报, 2005, 25(21): 41-44.
[12] 李辉, 韩力, 赵斌, 等. 风电机组等效模型对机组暂态稳定分析结果的影响[J]. 中国电机工程学报, 2008, 28(17): 105-111.
[13] 周世华, 李朝峰, 王开宇, 等. 风电齿轮箱传动系统的动力学建模[J]. 东北大学学报(自然科学版), 2014, 35(9): 1301-1305.
[14] Lee K, Im J, Choy I, et al. MPPT and yawing control of a new horizontal-axis wind turbine with two parallel-connected generators[C]//IEEE International Conference on Power Electronics & Ecce Asia. IEEE, 2011: 2618-2624.
[15] Ekanayake J B, Holdsworth L, Jenkins N. Comparison of 5th order and 3rd order machine models for doubly fed induction generator (DFIG) wind turbines[J]. Electric Power Systems Research, 2003, 67(3): 207- 215.
[16] Zhi Dawei, Xu Lie. Direct power control of DFIG with, constant switching frequency and improved transient performance[J]. IEEE Transactions on Energy Con- version, 2007, 22(1): 110-118.
[17] Nian Heng, Song Yipeng, Zhou Peng, et al. Improved direct power control of a wind turbine driven doubly fed induction generator during transient grid voltage unbalance[J]. IEEE Transactions on Energy Conver- sion, 2011, 26(3): 976-986.
[18] Sanchez A G, Molina M G, Rizzato Lede A M. Dynamic model of wind energy conversion systems with PMSG-based variable-speed wind turbines for power system studies[J]. International Journal of Hydrogen Energy, 2012, 37(13): 10064-10069.
[19] VladislavAkhmatov, Nielsen AH. Variable-spped wind turbines with multi-pole synchronous permanent magnet generators.Part I:Modelling in dynamic simulation tools[J]. Wind Engineering, 2003, 27(6): 531-548.
[20] Kallio S, Andriollo M, Tortella A, et al. Decoupled- model of Double-Star Interior-Permanent-Magnet syn- chronous machines[J]. IEEE Transactions on Industrial Electronics, 2013, 60(6): 2486-2494.
[21] 祝贺. 直驱永磁风力发电机组数学模型及并网运行特性研究[D]. 沈阳: 沈阳工业大学, 2013.
[22] 陈晓红, 王一飞, 尚鹏, 等. 永磁同步风力发电机转速桨距综合功率控制策略研究[J]. 可再生能源, 2014, 32(9): 1306-1311.
[23] Zou Jianxiao, Peng Chao, Yan Yan, et al. A survey of dynamic equivalent modeling for wind farm[J]. Renewable & Sustainable Energy Reviews, 2014, 40: 956-963.
[24] Zou Jianxiao, Peng Chao, Xu Hongbing, et al. A fuzzy clustering Algorithm-Based dynamic equivalent mode- ling method for wind farm with DFIG[J]. IEEE Transactions on Energy Conversion, 2015, 30(4): 1329-1337.
[25] 王荷生. 风电场等值建模及其暂态运行特性研究[D]. 重庆: 重庆大学, 2010.
[26] 潘学萍, 张弛, 鞠平, 等. 风电场同调动态等值研究[J]. 电网技术, 2015, 39(3): 621-627.
[27] Conroy J, Watson R. Aggregate modelling of wind farms containing full-converter wind turbine gener- ators with permanent magnet synchronous machines: transient stability studies[J]. Renewable Power Generation, IET, 2009, 3(1): 39-52.
[28] Mercado-Vargas M J, Gomez-Lorente D, Rabaza O. Aggregated models of permanent magnet synchronous generators wind farms[J]. Renewable Energy, 2015, 83: 1287-1298.
[29] 朱乾龙, 韩平平, 丁明, 等. 基于聚类-判别分析的风电场概率等值建模研究[J]. 中国电机工程学报, 2014, 34(28): 4770-4780.
[30] 徐玉琴, 王娜. 基于聚类分析的双馈机组风电场动态等值模型的研究[J]. 华北电力大学学报(自然科学版), 2013, 40(3): 1-5.
[31] 米增强, 苏勋文, 杨奇逊, 等. 风电场动态等值模型的多机表征方法[J]. 电工技术学报, 2010(5): 162- 169.
[32] Fernández L M, García C A, Saenz J R, et al. Equivalent models of wind farms by using aggregated wind turbines and equivalent winds[J]. Energy Conversion and Management, 2009, 50(3): 691-704.
[33] Garcia-Gracia M, Comech M P, Sallan J, et al. Modelling wind farms for grid disturbance studies[J]. Renewable Energy, 2008, 33(9): 2109-2121.
[34] 米增强, 苏勋文, 余洋, 等. 双馈机组风电场动态等效模型研究[J]. 电力系统自动化, 2010, 34(17): 72-77.
[35] 付蓉, 谢俊, 王保云. 风速波动下双馈机组风电场动态等值[J]. 电力系统保护与控制, 2012, 40(15): 1-6.
[36] 高远, 金宇清, 鞠平, 等. 考虑Crowbar动作特性的DFIG风电场动态等值研究[J]. 电网技术, 2015, 39(3): 628-633.
[37] 汪令祥. 永磁同步直驱型全功率风机变流器及其控制[D]. 合肥: 合肥工业大学, 2011.
[38] 夏玥, 李征, 蔡旭, 等. 基于直驱式永磁同步发电机组的风电场动态建模[J]. 电网技术, 2014, 38(6): 1439-1445.
[39] 龚陈雄, 王剑, 吴丹岳, 等. 永磁直驱型风电场的并网仿真研究[J]. 广东电力, 2014(2): 38-42, 110.
[40] 张琛, 李征, 蔡旭, 汪宁渤. 面向电力系统暂态稳定分析的双馈风电机组动态模型[J/OL]. 中国电机工程学报, 2016(20): 5449-5460.
[41] 訾鹏, 周孝信, 田芳, 等. 双馈式风力发电机的机电暂态建模[J]. 中国电机工程学报, 2015(5): 1106- 1114.
[42] 白雪峰, 倪以信. 电力系统动态安全分析综述[J]. 电网技术, 2004, 28(16): 14-20.
[43] 刘其辉, 韩贤岁. 双馈风电机组的通用型机电暂态模型及其电磁暂态模型的对比分析[J]. 电力系统保护与控制, 2014(23): 89-94.
[44] 石立宝, 戴世强, 徐政, 等. 大规模双馈型风电场并网的系统暂态稳定仿真[J]. 电力系统及其自动化学报, 2009, 21(4): 1-7.
[45] 张明理, 徐建源, 李佳珏. 含高渗透率风电的送端系统电网暂态稳定研究[J]. 电网技术, 2013, 37(3): 740-745.
[46] 迟永宁, 王伟胜, 刘燕华, 等. 大型风电场对电力系统暂态稳定性的影响[J]. 电力系统自动化, 2006, 30(15): 10-14.
[47] Hossain M J, Pota H R, Mahmud M A, et al. Investigation of the impacts of Large-Scale wind power penetration on the angle and voltage stability of power systems[J]. IEEE Systems Journal, 2012, 6(1, SI): 76-84.
[48] 汤蕾, 沈沉, 张雪敏. 大规模风电集中接入对电力系统暂态功角稳定性的影响(一): 理论基础[J]. 中国电机工程学报, 2015(15): 3832-3842.
[49] 汤蕾, 沈沉, 张雪敏. 大规模风电集中接入对电力系统暂态功角稳定性的影响(二): 影响因素分析[J]. 中国电机工程学报, 2015(16): 4043-4051.
[50] Lin L, Zhao H, Lan T, et al. Transient stability mechanism of DFIG wind farm and grid-connected power system[C]//PowerTech (POWERTECH), 2013 IEEE Grenoble. 2013:1-9.
[51] 于强, 孙华东, 汤涌, 等. 双馈风电机组接入对电力系统功角稳定性的影响[J]. 电网技术, 2013(12): 3399-3405.
[52] 田新首, 王伟胜, 迟永宁, 等. 双馈风电机组故障行为及对电力系统暂态稳定性的影响[J]. 电力系统自动化, 2015(10): 16-21.
[53] 罗煦之, 易俊, 张健, 等. 结合DFIG功率特性研究风电并网对系统功角稳定性的影响[J]. 电网技术, 2015, 39(12): 3401-3407.
[54] 卢锦玲, 徐超, 程晓悦, 等. 基于DFIG的变速风电机组对系统暂态稳定影响[J]. 电力系统及其自动化学报, 2016, 28(1): 68-73.
[55] 林俐, 杨以涵. 基于扩展等面积定则的含大规模风电场电力系统暂态稳定性分析[J]. 电力系统保护与控制, 2012, 40(12): 105-110, 115.
[56] 陈乾, 沈沉, 刘锋. 端口能量及其在风电系统暂态稳定分析中的应用[J]. 电力系统自动化, 2015(15): 9-16.
[57] 高峰, 黄鸣宇, 乔颖. 考虑低电压穿越能力的风火联运系统暂态稳定分析[J]. 电力科学与技术学报, 2015, 30(4): 40-47, 70.
[58] 梁立龙, 白雪峰. 计及风速相关性的含风电电力系统暂态稳定分析[J]. 电网技术, 2015(11): 3228-3232.
[59] 张波, 蒋海军. 基于风电不确定性的电力系统机电暂态过程[J]. 电网与清洁能源, 2016, 32(4): 44-51.
The Overview of Influence of Large Scale Wind Generation on Transient Stability of Power System
Lin Minwei Wen Buying
(College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350108)
In recent years, as the penetration of wind power in power system growing, the impact of wind farm integration on power system is larger. Firstly, this paper summarizes some relevant achievement such as wind power generation system modelling, wind farm equivalent modelling and transient stability of power system containing wind farm. Then, the summary and comparison of methods of transient stability analysis is proposed. At last, this paper forecast the developing trend of relativetechnology, and make some suggestions to the follow-up studies.
wind generation; VSCF; transient stability; time-domain simulation; direct method
林旻威(1992-),男,硕士研究生,主要研究方向为风电并网运行技术。

