水平井致密油储层近井和远井可压性研究
刘坤, 孙建孟, 陈心宇
(1.中国石油大学(华东)地球科学与技术学院, 山东 青岛 266580;2.中国石油川庆钻探国际工程公司, 四川 成都 610051)
0 引 言
致密油储层由于其物性较差,一般无自然产能或自然产能极低,现场多采用水平井加体积压裂的方式进行储层改造[1]。储层的可压性是进行压裂施工评估的关键要素,储层的可压性越好,储层也就越易形成复杂的裂缝网络,并获得较大的改造体积。储层的可压性分为近井可压性和远井可压性。国内外研究中对储层可压性的评价几乎全部局限于近井筒的测井探测深度范围,并利用脆性指数表征储层可压性。一些学者认为脆性指数法对影响因素考虑不够全面,因此,综合利用脆性指数和断裂韧性表征可压性[2-5]。由于基于测井参数表征的储层可压性只代表近井筒储层的特征,不能反映远井筒的可压性情况。因此,一些学者利用压裂施工曲线反求岩石力学参数[6-8],进而为评价远井可压性奠定了基础。
本文针对水平井致密油储层,研究其分段多簇射孔压裂的可压性情况。利用测井资料,求取脆性指数和断裂韧性,得到近井可压性指数;基于压裂施工曲线,反求各压裂段的岩石力学参数,从而得到远井脆性指数,同时利用地层破裂耗能表征地层破坏的难易程度,综合远井脆性指数和破裂耗能构建远井可压性指数,并分别与储层改造体积作相关分析,对压前预测和压后评估有很大的指导意义。
1 近井可压性评价研究
1.1 近井脆性指数评价研究
国内外学者多利用脆性指数表征岩石的可压性,并用于指导储层的压裂施工[9]。李庆辉[10]对现有脆性指数的计算方法总结了20种,测井中常用声波法和矿物组分法。
Rickman等[11]提出了根据弹性模量和泊松比量化表征岩石储层的脆性指数的计算公式,泊松比指示岩石受力后抵抗破坏的能力,弹性模量指示岩石破裂后维持裂缝的能力,弹性模量越高,泊松比越低,脆性越强。声波法测量结果为动态弹性模量和动态泊松比,需要转化为静态弹性模量和静态泊松比。
(1)
(2)
(3)
式中,IB为近井脆性指数,无量纲;E为静态弹性模量,GPa;Emax和Emin分别为研究层段最大和最小静态弹性模量,GPa;ν为静态泊松比,无量纲;νmax和νmin分别为研究层段最大和最小静态泊松比,无量纲。矿物组分法[12]利用岩石中脆性矿物占总矿物量的百分比表征脆性指数,初期仅石英被当成脆性矿物,后经进一步的研究表明除石英外还包括长石、云母和碳酸盐矿物等。
IB=(WQFR+WCarb)/WTot
(4)
式中,WQFR为石英、长石和云母的总含量;WCarb为碳酸盐矿物含量;WTot为总矿物量。
1.2 近井断裂韧性评价研究
断裂韧性是一项表征储层改造难易程度的重要因素,反映压裂过程中,裂缝形成之后维持裂缝向前延伸的能力[2]。对于Ⅰ型裂缝,基于Irwin断裂力学理论[13],当应力强度因子KI达到某一临界值KIC时,裂缝向前扩展,其中,KIC为断裂韧性,其值越小,水力压裂造缝能力越强,越有利于水力压裂[3]。当地层断裂韧性较小时,不在水力延伸路径上的天然裂缝极有可能发生剪切破坏,一旦水力裂缝有效地沟通天然裂缝就会形成复杂的裂缝网络。因此,地层的断裂韧性越小,地层的可压性程度越高[4]。
断裂韧性的值可通过实验测得,但操作十分复杂,且只能获得研究层段的离散数据。金衍等[14]根据大量实验,利用测井数据建立了预测深部地层岩石的Ⅰ型断裂韧性的等效计算方法,可获得研究井段的连续断裂韧性剖面。
0.517σt-0.3322
(5)
式中,σt为岩石抗拉强度,MPa;pc为围压,MPa。
1.3 近井可压性评价研究
为使水力压裂能够形成可连通的复杂缝网,可压裂层段应具有较高的脆性指数和较低的断裂韧性。构建近井可压性指数IF
IF=IB,nKIC,n
(6)
式中,IB,n为正向归一化的脆性指数,无量纲;KIC,n为反向归一化的断裂韧性,无量纲。IB,n和KIC,n定义为
(7)
(8)
式中,IB,max和IB,min分别为研究层段最大和最小脆性指数,无量纲;KIC,max和KIC,min分别为研究层段最大和最小断裂韧性,MPa·m0.5。
2 远井可压性评价研究
岩石力学参数关系到压裂施工工艺参数的优选,主要通过室内三轴岩心实验和测井资料解释获取。实验室三轴实验测试费时费力,而且费用较高。而对于测井资料,无论声波法还是矿物组分法都有其缺点,声波法要求测井必须测阵列声波测井资料,特别是对于水平井致密油储层,阵列声波测井资料匮乏,并且取心困难,以及需要动静态转换得到静态岩石力学参数;矿物组分法认为石英和方解石对岩石脆性指数贡献相同,但两者岩石力学性质有一定差异[15]。最重要的是,基于测井资料得到的可压性为近井筒的可压性情况,难以反映整个压裂过程的准静态过程。因此,需要研究一种简单易行、价格低廉、结果可靠的方法,从压裂施工本身所反馈的信息,去求取就地岩石力学参数。
2.1 远井岩石力学参数评价研究
蒋廷学[6]应用常规地面压裂施工和前置液阶段的瞬时停泵压力测试等资料,初步探讨了求取储层原位岩石力学参数的方法。该方法首先由地面施工压力计算井底压力,并由井底压力的增长模式确定裂缝的扩展形态。然后根据裂缝形态的不同,确定相应的计算公式。其实质就是利用裂缝宽度既与弹性模量有关,又与裂缝净压力有关的特点,建立不同时间的井口压力与弹性模量间的对应关系曲线。同时,利用泊松比与最小水平主应力的相关式,由最小主应力的变化曲线,求出了泊松比的变化曲线。田勇[16]在此基础上,建立了井底压力与考虑拟三维裂缝扩展模型时的就地岩石力学参数关联式。采用动态应力强度因子积分公式作为裂缝垂向延伸的判据,使新模型兼具拟三维模型的简单和真三维模型的准确,使得就地岩石力学参数的评价更符合实际。
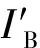
2.2 远井可压性评价研究
根据上文求出的远井岩石力学参数,可以构建远井脆性指数。压裂实践表明,单纯依靠岩石的脆性指数是不能完全判断地层的可压性,可从能量的角度去评价地层压裂的难易程度。在分段多簇压裂施工的过程中的前置液阶段,随着泵注排量不断提升,地层发生形变直到破裂。当压裂段地层达到破裂时所需要的能量越小,该压裂段越容易压裂;反之,地层越难压裂。破裂消耗的能量可简化为变形长度与变形期间基本恒定压力的乘积,用水力压裂施工参数表示,可等效为施工压力、施工排量和施工时间的乘积[17]。考虑到变形期间,压力和排量可能是一直变化的,必须采用破裂前阶段期间内井底施工压力与排量的乘积,并对时间进行积分求解

(9)
式中,P为破裂地层所消耗的能量;Q为泵注排量;t0为地层破裂所需要的时间。
由于水平井压裂段采用分段多簇射孔方式,在进行分段压裂设计时,段内部物性参数基本一致,可近似认为当前压裂段储层是均质的。在分簇射孔时,认为每一簇射孔均发生起裂,每簇射孔消耗的能量基本一致。为了便于比较分析,应先求出压裂段每簇射孔破裂的耗能Pi,然后对Pi进行归一化,得到压裂段单簇射孔破裂的耗能指数IP
IP=P/N
(10)
(11)
式中,N为压裂段的射孔簇数;Pmax和Pmin分别为研究区块破裂地层所消耗的最大能量及最小能量。
现场进行水力压裂的目的是形成复杂的裂缝网络系统,用最小的消耗,得到最大程度的油藏改善体积。因此可压性好的层段应该具有较高的脆性指数和较低的地层破裂耗能。鉴于此,远井脆性指数和耗能指数相结合,构建地层的远井可压性综合指标IF

(12)
3 应用效果实例分析
×3井为D区的1口水平井(见图1),水平段为致密油储层,测深1 880~2 520 m,垂深约为1 655 m,该井分7段进行体积压裂,其过程中,加入了示踪剂,对每段的产能进行跟踪监测,同时采用微地震裂缝监测技术,对储层压裂规模进行评价。
基于上述研究方法,计算了该井的近井脆性指数、断裂韧性和近井可压性指数;并对该井的7条主压裂施工曲线进行分析,反求了各压裂段的岩石力学参数,得到了远井脆性指数,并计算各压裂段的耗能指数,构建远井可压性指数。图1中第8道为测井计算断裂韧性和由压裂施工曲线计算的耗能指数;第9道为近井和远井脆性指数曲线道;第10道为近井和远井可压性曲线道;第11道为微地震监测各段造缝体积(VSR)及示踪剂跟踪监测各段产能。
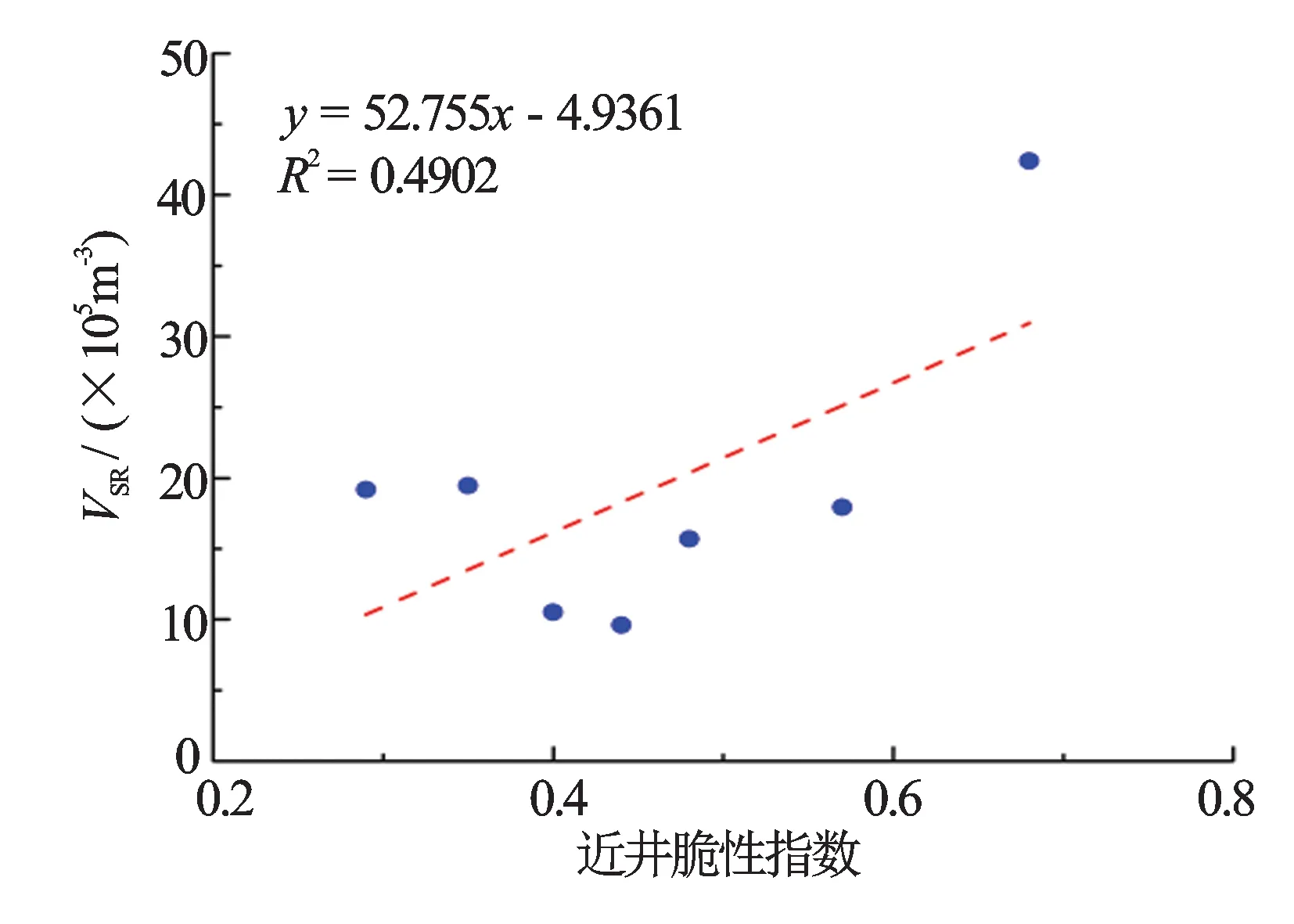
图2 近井脆性指数与VSR关系图

图3 远井脆性指数与VSR关系图

图4 近井可压性指数与VSR关系图
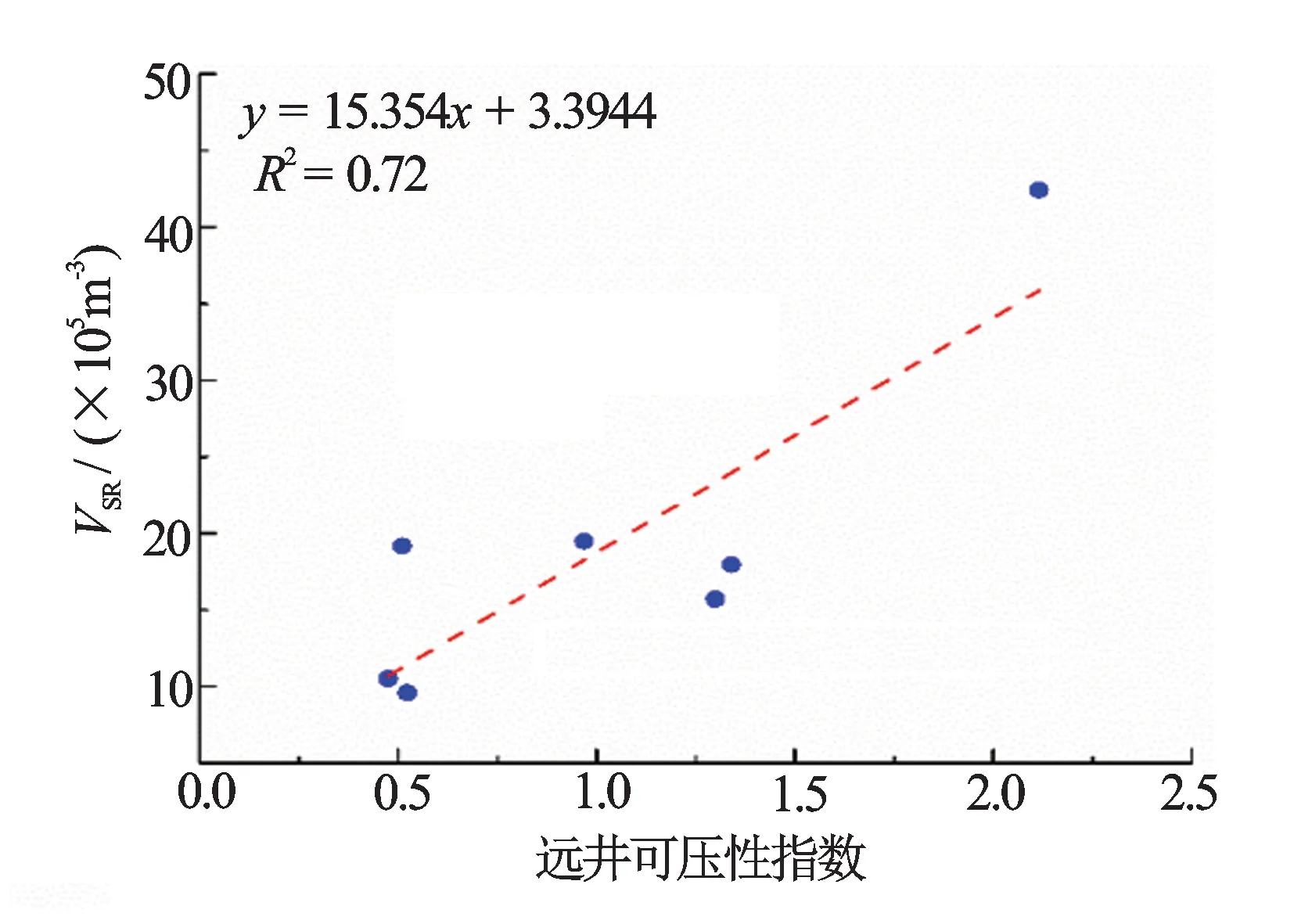
图5 远井可压性指数与VSR关系图
近井和远井脆性指数分别与VSR对比分析(见图2、图3)可以看出,脆性指数越高,储层改造体积越大,但两者与VSR相关性较差,并不能很好地反映储层的改造体积。分析近井和远井可压性指数分别与VSR的关系(见图4、 图5)可以看出,可压性指数较脆性指数更能反映储层改造体积的情况,且远井可压性要优于近井可压性。远井可压性考虑了压裂段整个地层的性质,因此,远井可压性更能反映地层的实际改造情况。近井和远井可压性指数与示踪剂跟踪监测各压裂段产能关系分别见图6和图7。

图6 近井可压性指数与产能关系图
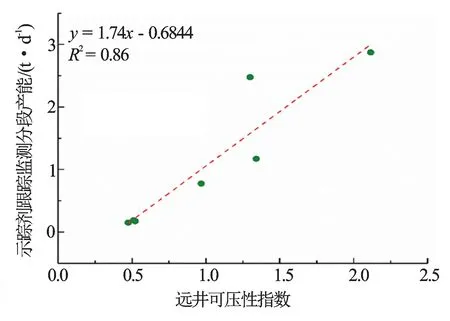
图7 远井可压性指数与产能关系图
4 结 论
(1) 基于测井资料,讨论了近井脆性指数和近井可压性指数的求取方法;利用压裂施工曲线反求岩石力学参数及远井脆性指数,计算破裂耗能指数,表征地层压裂的难易程度,构建远井可压性指数。
(2) 从近井和远井脆性指数、近井和远井可压性指数分别与VSR的关系可知,脆性指数反映储层改造体积有限,可压性指数更能反映储层改造体积情况,远井可压性优于近井可压性,且可压性指数与产能趋势基本一致,表明这2种方法可行。
参考文献:
[1] 许冬进, 尤艳荣, 王生亮, 等. 致密油气藏水平井分段压裂技术现状和进展 [J]. 中外能源, 2013, 18(4): 36-41.
小学一年级儿童(约6岁)的阅读能力呈现出很大差别。有的能够独立阅读,有些却无法拼读单词。因此,在学步期及学龄前阶段家庭为儿童营造良好的阅读氛围有助于上学后迅速适应学习环境,理解教学指令,消化教学内容。
[2] 袁俊亮, 邓金根, 张定宇, 等. 页岩气储层可压裂性评价技术 [J]. 石油学报, 2013, 34(3): 523-527.
[2] 孙建孟, 韩志磊, 秦瑞宝, 等. 致密气储层可压裂性测井评价方法 [J]. 石油学报, 2015(1): 74-80.
[4] 赵金洲, 许文俊, 李勇明, 等. 页岩气储层可压性评价新方法 [J]. 天然气地球科学, 2015, 26(6): 1165-1172.
[5] JIN X, SHAH S N, ROEGIERS J C, et al. Fracability Evaluation in Shale Reservoirs——An Integrated Petrophysics and Geomechanics Approach [J]. Spe Journal, 2014, 20(3): 518-526.
[6] 蒋廷学, 汪永利, 丁云宏, 等. 由地面压裂施工压力资料反求储层岩石力学参数 [J]. 岩石力学与工程学报, 2004, 23(14): 2424-2429.
[7] 刘登峰. 煤层气井压裂施工资料反演岩石力学参数及压后产能预测研究 [D]. 成都: 西南石油大学, 2006.
[9] KAHRAMAN S, ALTINDAG R. A Brittleness Index to Estimate Fracture Toughness [J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41(2): 343-348.
[10] 李庆辉, 陈勉, 金衍, 等. 页岩脆性的室内评价方法及改进 [J]. 岩石力学与工程学报, 2012(8): 1680-1685.
[11] RICKMAN R, MULLEN M J, PETRE J E, et al. A Practical Use of Shale Petrophysics for Stimulation Design Optimization: All Shale Plays are not Clones of the Barnett Shale [C]∥SPE Annual Technical Conference and Exhibition, Society of Petroleum Engineers, 2008.
[12] JARVIE D. Finding Bypassed or Overlooked Pay Zones Using Geo-chemistry Techniques [R]. IPTC 12918, 2008.
[13] IRWIN G R. Analysis of Stresses and Strains Near End of a Crack Traversing a Plate [J]. J appl mech, 1956, 24: 361-364.
[14] 金衍, 陈勉, 张旭东. 利用测井资料预测深部地层岩石断裂韧性 [J]. 岩石力学与工程学报, 2001, 20(4): 454-456.
[15] 李霞, 周灿灿, 赵杰, 等. 泥页岩油藏测井评价新方法——以松辽盆地古龙凹陷青山口组为例 [J]. 中国石油勘探, 2014, 19(3): 57-65.
[16] 吴华. 地层条件下岩石力学特性研究 [D]. 青岛: 中国石油大学, 2010.
[17] 蒋廷学, 卞晓冰, 苏瑗, 等. 页岩可压性指数评价新方法及应用 [J]. 石油钻探技术, 2014, 42(5): 16-20.

