ECOS过套管电阻率测井响应自适应hp有限元数值模拟

张盼, 王正楷, 邓少贵

(中国石油大学地球科学与技术学院, 山东 青岛 266580)

0 引 言

套管井电阻率测井响应模拟的主要困难在于金属套管和其他介质(水泥环、地层等)的强电导率对比度所导致的计算精度问题[1-2]。传输线方程较好描述了套管井环境场的分布特点[3],成为过套管电阻率测井理论计算的重要方程[4]。刘福平等[5]建立了改进型传输线模型,把影响因素吸收到传输线方程的系数中,假定介质参数分块变化,提出了改进型传输线方程的递推算法,在对各种因素的考察中获得广泛的应用[6-8]。但是,当套管纵向单位长度电阻、水泥环单位厚度电阻或地层电阻率非分块均匀时,改进型传输线的递推算法变得困难。为提升改进型传输线的适用性和计算精度,采用自适应hp有限元求解具有灵活性。

本文在自适应hp有限元框架下[9-12],求解ECOS过套管电阻率的改进型传输线方程,自动调节网格剖分大小h和单元插值函数阶数p,寻找适合问题解本身特征的拟优化的网格。在相同自由度条件下,自适应hp有限元能够达到最高的计算精度。实际计算中,基于先验信息的拟最优网格的几乎是不可行的。自适应hp有限元从粗网格迭代开始,不断寻找当前粗网格的细化网格,有限元误差可控。

1 ECOS过套管电阻率的测井原理

ECOS的过套管电阻率测井仪器结构如图1所示,以测量电极N为中心上下对称分布1对测量电极M1、M2和发射电极A1和A2,测量电极N到测量电极M1的距离为0.5 m,到发射电极A1的距离为1.8 m。测井时,仪器推靠到井壁固定,上发射电极A1发射电流强度为I1的电流,分别测量测量电极N的电压UN(I1)、测量电极M1与N的电压和测量电极M2与N的电压;下发射电极A2发射电流强度为I2的电流,分别测量测量电极N的电压UN(I2),测量电极M1与N的电压和测量电极M2与N的电压,根据电压的线性叠加特性,得到过套管的电阻率表达式

(1)

式中,UN(I1)、UN(I2)分别为上供电电极和下供电电极供电时,测量电极N同套管的接触点的电位;ΔUN(I1)、ΔUN(I2)分别为上供电电极和下供电电极供电时,电极系的2个电极M1、M2的一阶差分;Δ2UN(I1)、Δ2UN(I2)分别为上供电电极和下供电电极供电时,3个测量电极同套管接触点之间套管段上电位的二阶差分;I1、I2分别为A1和A2供电电极向套管注入的电流。

2 一维自适应hp有限元方法

2.1 过套管电阻率的传输线方程

设单极供电电极位于井轴线上z点,则产生的电位沿井轴的分布可表述为

(2)

当Rr/Rz≫1时,套管边界面上的电流近似垂直金属套管壁流向地层[13],径向电流可以表示为

(3)

式中,U(z)为井轴z处的电位,V;Jz(z)为经过同一坐标的套管横截面的电流,A;Jr(z)为由单位长度深度段井壁进入周围地层的电流,A/m;Rr为单位厚度介质对电流Jr(z)的电阻,Ω/m;Rz为单位长度套管对轴向电流Jz(z)的电阻,Ω/m。

以发射电极中心圆柱的中心作一个套管圆柱体,应用恒定电流的连续性方程,即

∮sJ·ds=I

(4)

将式(4)整理得

(5)

式中,I表示在z0点施加的直流电流的强度,A。

考虑边界条件,套管壁上的电势满足下列边值问题

u|Γ=0

(6)

根据Galerkin方法,式(6)等价成下列的问题

(7)

2.2 变阶插值函数

自适应hp有限元要求求解区域单元上的形状函数为层状形状函数,即高阶的形状函数包含低阶的形状函数,单元上的形状函数通过拼合而构成有限元空间的基函数[14]。通常情况下,选择Lobatto基函数作为自适应hp有限元的基函数。它是由2个一阶函数和多个高阶函数组成,k阶Lobatto基函数定义为

(8)

(9)

(10)

式中,Lk(x)为k次勒让德多项式,其定义为

(11)

2.3 投影型插值方法

投影型插值是单元顶点上的插值和单元内部投影相结合的拟合方法,它是自适应hp有限元自适应策略的核心组成部分[15]。投影型插值函数定义:假设某个单元上连续函数u,定义在[a,b]上到的p阶层次形状函数为φ1,φ2,φ3,i(i=1,2,…,p-1),则投影型插值函数为

(12)

式中,u1=u(a),u2=u(b),u3,j由在单元内部的投影系数求得下列的线性方程得到

(13)

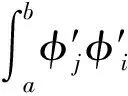
投影型插值保证插值算子是局部的,它只与单个单元上的解的信息有关;是整体连续的,每个单元的算子在整个网格连续;是最优的,它具有整体插值的特性,对h和p都是渐近收敛的。这些特点使得自适应hp策略效率更高。

2.4 自适应hp策略

自适应hp迭代是从一个粗网格开始,利用参考解在粗网格单元多种可能细化网格下的投影型插值的误差相对大小,寻找当前粗网格相对应的拟最优细化网格。当前粗网格的拟最优细化网格满足

hpopt=

(14)

实际上,真解u是未知的,采用参考解来近似。假设给定的当前粗网格单元尺寸为h和网格单元上的插值函数的阶数p,将每个单元二分变成2个等尺寸单元,变成h/2,每个单元上的阶数提高1阶,在新的全局一致细化网格上求得的解叫做当前粗网格下的参考解,记为uh/2,p+1。利用参考解和投影型插值,式(14)的全局优化问题可以通过粗网格每个单元上局部的优化问题来求解,将每个单元上增加的单位个自由度误差下降最大值称为误差下降速率,其表达式为

(15)

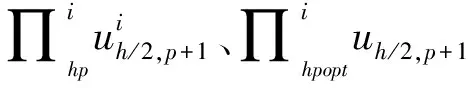
当前粗网格中每个单元的最优化的细化单元采用枚举的方式获得,枚举的细化单元的自由度个数介于当前粗网格单元和当前粗网格单元的参考单元自由度个数之间。

2.5 自适应hp算法

给定初始的粗网格单元和每个单元上插值函数的阶数,一般取1～2阶。

步骤1:计算当前粗网格上的有限元的解,记为uhp。

步骤2:对粗网格上的每个单元,二分单元h并将得到每个单元的多项式阶数p提升到p+1,计算有限元的参考解uh/2,p+1,如果相对能量误差‖uh/2,p+1-uh,p‖/‖uh/2,p+1‖小于容忍误差,停止迭代,并输出hp有限元的解uh/2,p+1,否则转入步骤3。

步骤3:将参考解投影到粗网格中的每个单元所有可能细化单元上,利用式(15)计算误差下降速率ri,确定每个单元误差下降速率的h细化和p细化。

3 测井响应计算

3.1 方法验证

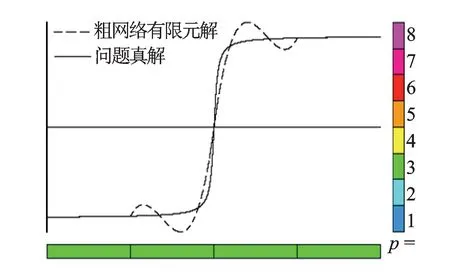
图3 问题真解和粗网格有限元的解

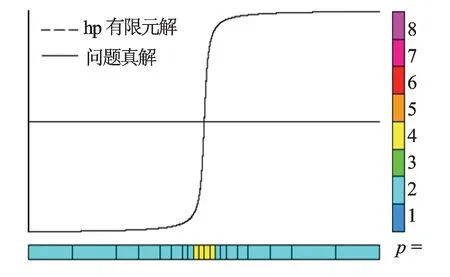
图4 问题真解和自适应hp有限元的解

为了验证自适应hp有限元方法的有效性和程序的正确性,给出一个具有解析解的边值问题,该解析解在中心部分剧烈变化。图3为问题真解和粗网格有限元的解,图3中的横坐标表示求解区域,纵坐标表示解的大小,实线为实际问题的解,虚线为粗网格剖分下的有限元的解。图3中低端部分表示网格的大小,颜色表示阶数。图3中右侧部分是颜色刻度,不同的阶数对应不同的颜色。可以看出,求解该边值问题的初始网格为4个单元,每个单元的插值函数都为3阶,粗网格的有限元解与真解之间的误差较大。图4为问题的真解和自适应hp有限元解,计算中相对能量误差取为0.1%,从图4中可以看出二者吻合相当好。细化网格集中在问题真解剧烈变化,说明基于参考解投影型插值的自适应hp策略捕捉到问题真解的剧烈变化的特性,充分体现了自适应hp方法的正确性和有效性(见图4)。

3.2 金属套管异常条件影响

为研究金属套管电导率异常对测井响应影响,所建研究模型的金属套管的电导率为5×106S/m,深度分别为1 993.5～1 995.5 m、1 999.5～2 000.5 m和2 004.5～2 006.5 m的电导率为3×106S/m。图5为在该模型下的过套管电阻率测井响应,图5中蓝线为地层的真电阻率,带点的实线为过套管电阻率的测井响应。从图5中可以看出,在金属套管电导率发生突变的地方,视电阻率出现类似一个周期正弦的异常,该周期的宽度约为电极系中M1和M2之间的距离(1 m),金属套管高电导率部分对应约为半个周期的低值部分,而金属套管低电导率部分对应约为半个周期的高值部分,如果金属电导率分段异常部分小于M1和M2之间的距离,过套管电阻率异常将出现重叠。

图5 金属套管异常条件下过套管电阻率测井响应

假设金属套管的电导率为5×106S/m不变,在深度为1 982～1 986 m、1 990～1 994 m和1 998～2 002 m的电导率分别为3×106、2×106、4×106S/m。图6为该金属套管电导率条件下的过套管电阻测井响应,图6中,除了图5中展示的特点,类似正弦的异常值的大小与金属套管电导率的突变值有关,金属套管的突变值越大,过套管电导率的异常值越大。

图6 金属套管异常条件下过套管电导率

图7为金属套管电导率线性变化模型,图8为对应的过套管电阻率测井响应,结合这2张图可以看出,金属套管线性变化部分对应的过套管电阻率没有出现异常,异常值出现在金属套管电导率导数突变的地方,异常值随线性变化率增大而增大。一般情况下,异常值通常很小。

图7 金属套管电导率线性变化模型

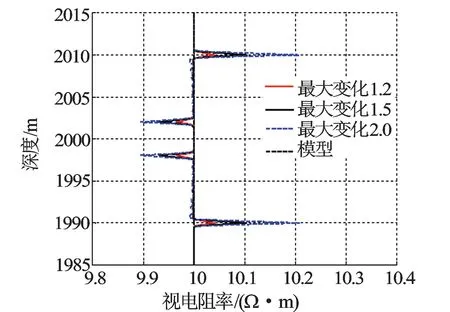
图8 金属套管电导率线性变化过套管电阻率测井响应

对于金属套管电导率正弦变化的情形,视电阻率也出现异常,异常的低值与套管的电导率的高值对应,异常的高值与套管电导率的低值对应,但电导率的异常值一般很小。

3.3 围岩电阻率影响

图9为分层地层的过套管电阻率测井响应。该模型中背景电阻率为2 Ω·m,深度1 994～1 995 m、1 999～2 001 m、2 005～2 008 m之间为3层厚度不同电阻率为10 Ω·m的地层。从图9中可以看出,ECOS过套管电阻率纵向分辨率的极限为1 m,由于计算中记录点长度为0.1 m,在层厚为1 m的地层中最多只有一个点反映到地层的真实电阻率,其余各点都受到围岩的影响。当记录点长度变大时,测量到围岩的影响就愈加明显。记录点长度小于1 m时,层厚大于2 m的地层在实际测井中受围岩的影响可以不计。图10为地层电阻率为正弦电阻率变化,视电阻率大致能够反映原来地层的形态,在高值点由于受到上下低阻围岩的影响,视电阻率变小;在低值点由于受到上下高阻围岩的影响,视电阻率变大。

图9 分层地层的过套管电阻率测井响应

图10 地层电阻率连续变化时测井响应

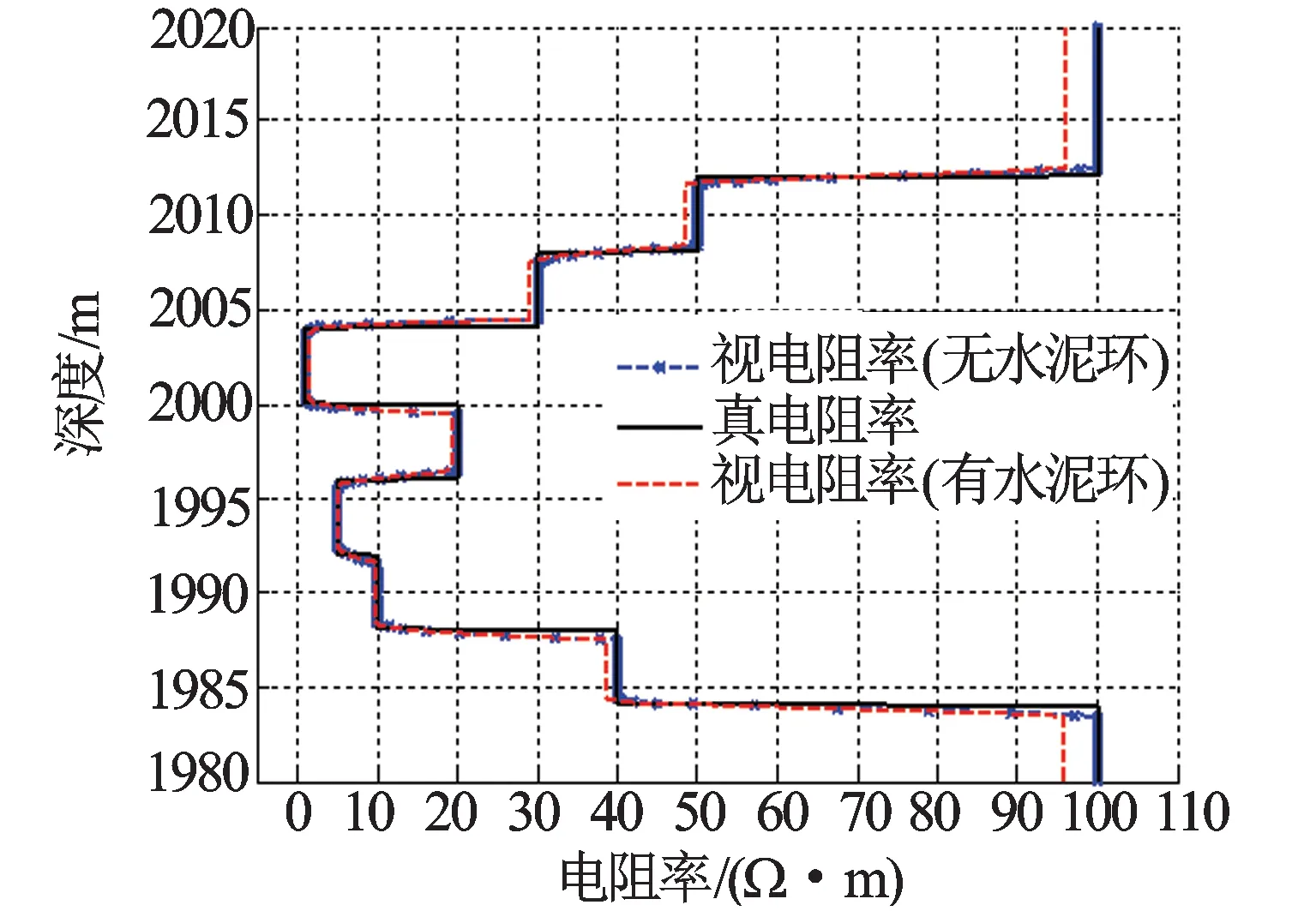
图11 水泥环存在时过套管电阻率测井响应

3.4 水泥环的影响

图11为水泥环存在时过套管电阻率测井响应。计算模型:套管的电导率1×105S/m,水泥环的厚度为5 cm,电阻率为5 Ω·m,共有10层地层(见图11)。图11中,水泥环电阻率大于地层电阻率,水泥环存在使视电阻率增加;水泥环电阻率等于地层电阻率,水泥环存在不影响电阻率;水泥环电阻率小于地层电阻率,水泥环的电阻率存在使视电阻率降低,且二者差异越大,影响越明显。

4 结 论

(1) 采用一维自适应hp有限元求解了ECOS过套管电阻率在不同条件下的测井响应,数值计算结果表明,该方法适应性强和计算精度高,适合于介质参数连续变化等复杂条件下问题的求解。

(2) 金属套管电导率的连续变化对ECOS过套管电阻率视电阻率的影响与间断变化的影响特征不同,通常条件下,连续变化的影响很小,可以忽略。

(3) 水泥环电阻率连续变化和地层电阻率连续变化对ECOS过套管电阻率的影响与相应参数间断变化特征类似。

参考文献:

[1] SINGER B H, FANINI O. Through-casing Resistivity: 2-D and 3-D Distortions and Correction Techniques [C]∥ SPWLA 36th Annual Logging Symposium, June 26-29, 1995.

[2] 刘福平, 陈小安, 杨长春. 过套管电阻率测井响应数值模拟研究进展 [J]. 地球物理学进展, 2011, 26(6): 2018-2025.

[3] KAUFMAN A A. The Electrical Field in a Borehole With a Casing [J]. Geophysics, 1990, 55(1): 29-38.

[4] KAUFMAN A A. WIGHTMAN W E. A Transmission-line Modelfor Electrical Logging Through Casing [J]. Geophysics, 1993, 58(12): 1739-1747.

[5] 刘福平, 高杰, 包德洲, 等. 实际井眼条件下过套管电阻率测井响应的传输线方程的正演算法 [J]. 地球物理学报, 2007, 50(6): 1905-1913.

[6] 高杰, 刘福平. 过套管电阻率测井方法研究 [C]∥ 第四届中俄测井国际学术交流会 [M].北京: 石油工业出版社, 2006: 339-349.

[7] 高杰, 刘福平, 保德州, 等. 非均匀套管井中的过套管电阻率测井响应 [J]. 地球物理学报, 2008, 51(4): 1255-1261.

[8] 魏宝君, 田坤, 张旭, 等. 模拟过套管电阻率测井响应的递推矩阵方法 [J]. 中国石油大学学报: 自然科学版, 2011, 35(6): 59-65.

[9] PARDO D, DEMKOWICZ L F, TORRES-VERDIN, et al. A Goal-oriented Hp-adaptive Finite Element Method with Electromagnetic Applications. Part I: Electrostatics, Int. J. Numer [J]. Methods Engrg. 2006, 65(8): 1269-1309.

[10] VARCIACASTILLO L E, PARDO D, GARCA-CASTILLO L E, et al. A Two-dimensional Self-adaptivehpFinite Element Method for the Characterization of Waveguide Discontinuities. Part I: Energy-norm Based Automatic Hp-adaptivity [J]. Comput. Methods Appl. Mech. Engrg., 2007, 196: 4823-4852.

[11] PARDO D, DEMKOWICZ L F, TORRES-VERES C, et al. Simulation of Resistivity Logging-while-drilling (LWD) Measurements Using a Self-adaptive Goal-orientedhp-finite Element Method [J]. SIAM J. Appl. Math, 2006, 66(6): 2085-2106.

[12] KURTZ J, DEMKOWICZ L F. A Fully Automatichp-adaptivity for Elliptic PDEs in Three Dimensions [J]. Computer Methods in Applied Mechanics and Engineering, 2007(196): 3534-3545.

[13] 刘福平, 陈小安, 赵宝成, 等. 过套管电阻率测井高电阻率层段不稳定性分析 [J]. 测井技术, 2013, 37(01): 85-89.

[14] 李辉, 刘得军, 刘悦, 等. 基于自适应hp-FEM的过套管电阻率测井仪器响应数值模拟 [J]. 地球物理学进展, 2013, 28(06): 3243-3253.

[15] DEMKOWICZ L F. Computing withhp-Adaptive Finite Elements, Vol. I. One and Two Dimensional Elliptic and Maxwell Problems [M]. Taylor and Francis: Chapman & Hall/CRC Press, 2007.