带指向约束的多目标调零天线*
曾浩 周建文 王秋实 王洪良 何海丹
(1. 重庆大学 通信工程学院, 重庆 400044; 2. 西南电子技术研究所, 四川 成都 610036)
带指向约束的多目标调零天线*
曾浩1,2周建文1王秋实1王洪良1何海丹2
(1. 重庆大学 通信工程学院, 重庆 400044; 2. 西南电子技术研究所, 四川 成都 610036)
在卫星导航接收机中,传统调零天线无法形成对卫星信号的主瓣指向.为了能同时形成多个天线方向图主瓣,并分别对准不同卫星信号,从而提高阵列增益,文中引入导向约束条件,采用直接矩阵求逆方法求解每个卫星信号的最优权矢量解,并完成波束合成;分析了文中算法的运算量,给出了阵列增益的解析表达式.研究表明,文中算法不仅抑制了外部干扰,而且克服了卫星信号间的相互干扰,形成了对每个卫星信号的主瓣指向,提高了输出信噪比.方向图和期望信号输出信干噪比的仿真结果验证了该算法的有效性.
天线阵列;干扰抑制;最优化
卫星导航系统在军事和人们日常生活中发挥了重要的作用,但卫星信号非常微弱,在存在带内干扰情况下接收机很难对其有效接收[1-2].已有的卫星导航接收机调零天线利用功率倒置准则来获得阵列加权矢量,比相控阵天线更能有效地抑制干扰[3-4].为了提高调零天线的抗干扰数量,文献[5]采用了极化敏感阵列.为了提高抗宽带干扰能力,文献[6]提出了空时二维调零天线.但上述调零天线的阵列方向图仅仅是在干扰方向形成零陷,没有明显的主瓣指向卫星方向,故对卫星信号没有获得阵列增益.同时,其他卫星信号相对于期望卫星信号而言也是干扰的,但这个干扰没有被抑制.雷达领域和移动通信领域中的自适应阵列天线可以在抑制干扰的情况下,形成主瓣并获得阵列增益,但只适用于单目标系统[7-8].在卫星导航中,接收机必须同时接收至少4颗卫星信号才能正常工作,因此,这是一个多目标系统.把自适应阵列天线进行多目标扩展,就可以应用于卫星导航接收机中,同时获得阵列增益和更好的抗干扰功能.
为了能同时形成多个天线方向图主瓣,并分别对准不同卫星信号,从而提高阵列增益,文中引入导向约束条件,建立信号模型,采用直接矩阵求逆方法求解每个卫星信号的最优权矢量解,分析了文中算法的运算量,给出了阵列增益的解析表达式,最后通过方向图仿真和期望信号输出信干噪比仿真验证算法的有效性.
1 信号模型
为实现抗干扰功能,文中采用阵列天线空域滤波方法.首先设阵列为均匀线阵,阵元个数为M,阵元都是理想的全向天线,电磁波满足远场入射和窄带条件,忽略通道不一致性和互耦的影响.空间有I个卫星信号si(t),入射角为θi,同时存在J个干扰信号mj(t),入射角为θj,则阵列接收信号矢量x(t)为
x(t)=[x1(t),x2(t),…,xM(t)]T=
(1)
式中,xm(t)为第m(m=1,2,…,M)个阵元接收信号,方向矢量v(θ)为与入射角θ相关的函数,n(t)为阵列接收噪声矢量.如果阵元间距为载波半个波长,方向矢量仅仅取决于信号入射角θ,即
v(θ)=[1,e,…,e]T
(2)
n(t)=[n1(t),n2(t),…,nM(t)]T
(3)则各个阵元接收的噪声信号可认为是独立同分布的.
对于单目标自适应阵列天线,其基本结构如图1所示.
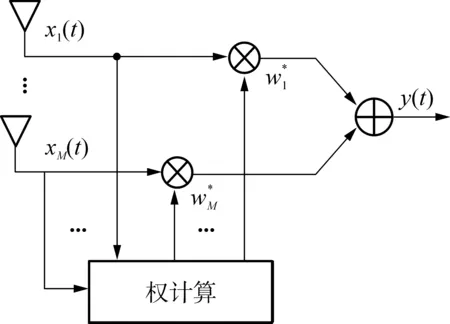
图1 单目标自适应阵列天线示意图Fig.1Schematicdiagramofsingle-objectadaptivearrayantenna
信号经过波束合成后的输出信号为
y(t)=wHx(t)
(4)
式中,权矢量w=[w1,w2,…,wM]T.
阵列输出信号功率可以表示为
Py=E[y(t)y*(t)]=Ps+Pj+Pn
(5)
式中,E[·]表示求随机过程的期望,Ps、Pj、Pn分别为期望信号、干扰信号和噪声的输出功率.需要强调的是,对于I个卫星信号中的某个信号,其余的I-1个卫星信号都应该被视为干扰,即此时干扰数量为J+I-1.对于一个阵列天线,其方向图等于阵因子与阵元因子的乘积.由于阵元为理想全向天线,所以方向图仅仅取决于阵因子,即
(6)
2 约束指向下的调零天线
2.1 最优化问题描述
卫星导航接收机是一个多目标系统,其中的每个目标都进行独立的波束合成.其系统结构框图如图2所示,每个波束合成结构如图1所示.对于第i个目标卫星信号,假设其权矢量为wi=[wi1,wi2,…,wiM]T,对应的输出信号为
(7)
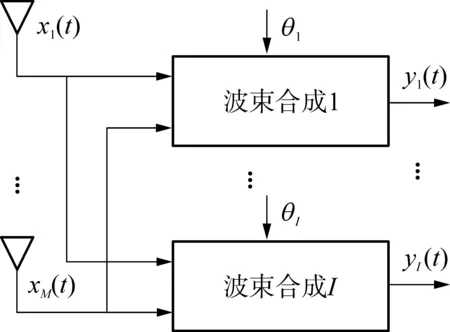
图2 多目标波束合成系统结构框图
Fig.2Structureblockdiagramofmultipleobjectsbeamformingsystem
为了在获得阵列增益的同时能抑制干扰,需要建立合适的最优化目标函数.首先,根据阵列方向图表达式,若第i个信号增益保持为1,则约束方程为
(8)
其次,为了抑制干扰,阵列输出信号yi(t)的功率应该最小,称为最小功率准则[9-11].基于上述两点,权值求解的最优化问题可以表述为
(9)
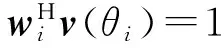
2.2 最优权矢量求解
可以采用拉格朗日乘子算法[12-13]求解上述最优权矢量解.通过施加约束条件(8),可得到第i个卫星信号的最小化函数为
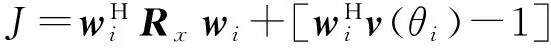
(10)
式中,Rx为接收信号的协方差矩阵,i为一个未知常数.对wi求复梯度,并令其等于0,可以得到

(11)
(12)
有
(13)
2.3 自适应滤波算法
自适应滤波算法是在工程中计算权矢量最优解的方法.直接矩阵求逆(DMI)、最小均方[14-15](LMS)和迭代最小二乘(RLS)是3种基本的自适应滤波算法.由于LMS和RLS均存在步长确定问题,所以其性能往往受输入信号条件的限制而不稳定.采用DMI方法只需要对协方差矩阵进行估计,并完成矩阵求逆运算,就可以得到稳定的输出.协方差矩阵采用有限个快拍进行估计,首先构造数据矩阵X=[x(1),x(2),…,x(K)],其中矩阵的每一列为接收信号矢量的一个时刻的采样快拍,则估计的协方差矩阵为
(14)
协方差矩阵估计误差对波束合成性能有重要的影响,根据文献[16]的分析,快拍数K>2M就可以满足一般的工程需求.对于不同的卫星信号,由于其输入信号是相同的,因此协方差矩阵仅仅需要计算一次.把协方差矩阵估计值代入最优权矢量解(9),就可以完成波束合成.
3 算法性能分析
3.1 运算量统计
传统的调零天线是一个迭代求权的过程,在采用K个快拍的情况下(阵元个数为M),其运算主要包括求取迭代步长μ和迭代求权.求μ的复数乘法运算量为M3+(K2-1)M2+M,迭代求权的运算量为(M2+M+1)K,该算法复数乘法的总计算量为M3+M2(K2+K-1)+M(1+K)+K.
在与传统调零天线相同的条件下,DMI算法求权主要包括对采样数据的协方差矩阵估计、求逆以及利用式(13)进行计算.考虑单个目标情况下,其对采样数据的协方差矩阵估计及求逆的复数乘法计算量为M3+(3+K2)M2-M,求取协方差矩阵逆矩阵后,代入式(13),计算量为2M2+M,故DMI算法的复数乘法总运算量为M3+(5+K2)M2.
使用双核Intel Core I5-4590@3.30 GHz进行仿真,计算不同快拍数K下的运行时间,结果如表1所示.从表中可以看出,单目标带指向约束的调零天线的运算量远小于传统调零天线,但若仅考虑4个目标,则其运算量与传统天线相当.

表1 不同快拍下的运行时间
3.2 输出信干噪比计算
阵列增益定义为阵列输出与单个阵元输入信干噪比(SINR)的比值.对于第i个目标卫星信号,其输入功率可表示为
(15)
输入干扰功率和噪声功率分别为
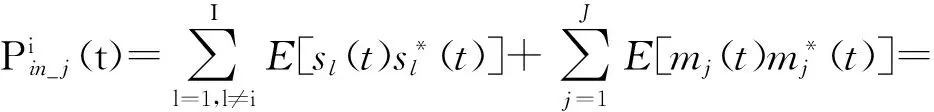
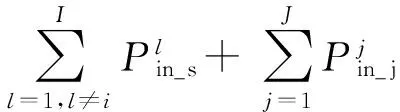
(16)
(17)
显然,输入的SINR为
(18)
同样地,考虑波束合成后的输出信号,根据约束条件(8),此时第i个卫星信号的输出功率为
(19)
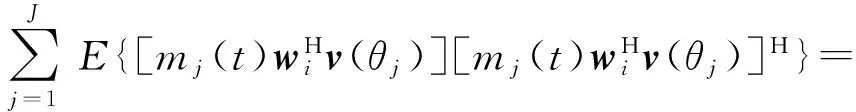
(20)
(21)
从而得到输出的SINR为
(22)阵列增益为
(23)
式中,A=Pin_n.
4 仿真实验
为了验证带指向约束的多目标调零天线性能,文中通过方向图和输出信干噪比两个指标与传统无指向约束的调零天线进行比较.考虑到实际天线阵列尺寸,仿真采用阵元数M=10的均匀线阵,阵元间距为波长的一半,期望信号的入射角(θ)为-50.0°、-24.5°、29.0°、60.0°,信噪比(SNR)均为-10 dB,干扰信号的入射角为3°,干噪比为60 dB,快拍数K=5 000.4.1 方向图仿真
图3为两种天线的阵列方向图,其中多目标调零天线的入射角为60.0°.从图中可以看出:两种天线的阵列方向图都能在干扰方向产生零陷,但文中多目标调零天线的阵列方向图在期望方向角形成明显的主瓣,波束指向期望信号角为60.0°,故提高了期望信号的增益;文中多目标调零天线在其他3个卫星信号角(-50.0°,-24.5°,29.0°)的阵列方向图也形成了零陷,只是深度较小,对其他卫星信号的抑制相对于当前期望卫星信号而言是有意义的.进一步比较两种天线对干扰的抑制情况,由图3可知,文中多目标调零天线的零陷深度为-150.00 dB以下,而传统天线的零陷深度为-70.71 dB.这主要是由传统天线的步长选择决定的,减小步长可以加深零陷,但收敛速度变慢,故稳健性不如文中天线.
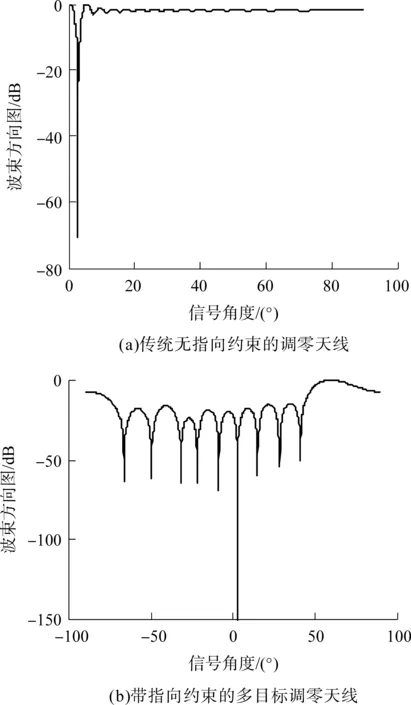
图3 两种天线的阵列方向图
Fig.3Arraypatternsoftwoantennas
图4是多目标情况下的方向图,每个目标卫星信号在干扰方向均形成了-150.00dB左右的零陷,在其他卫星信号方向也形成了一定深度的零陷.因在各种卫星信号入射方向均形成了显著的主瓣,故提高了该卫星信号的增益.
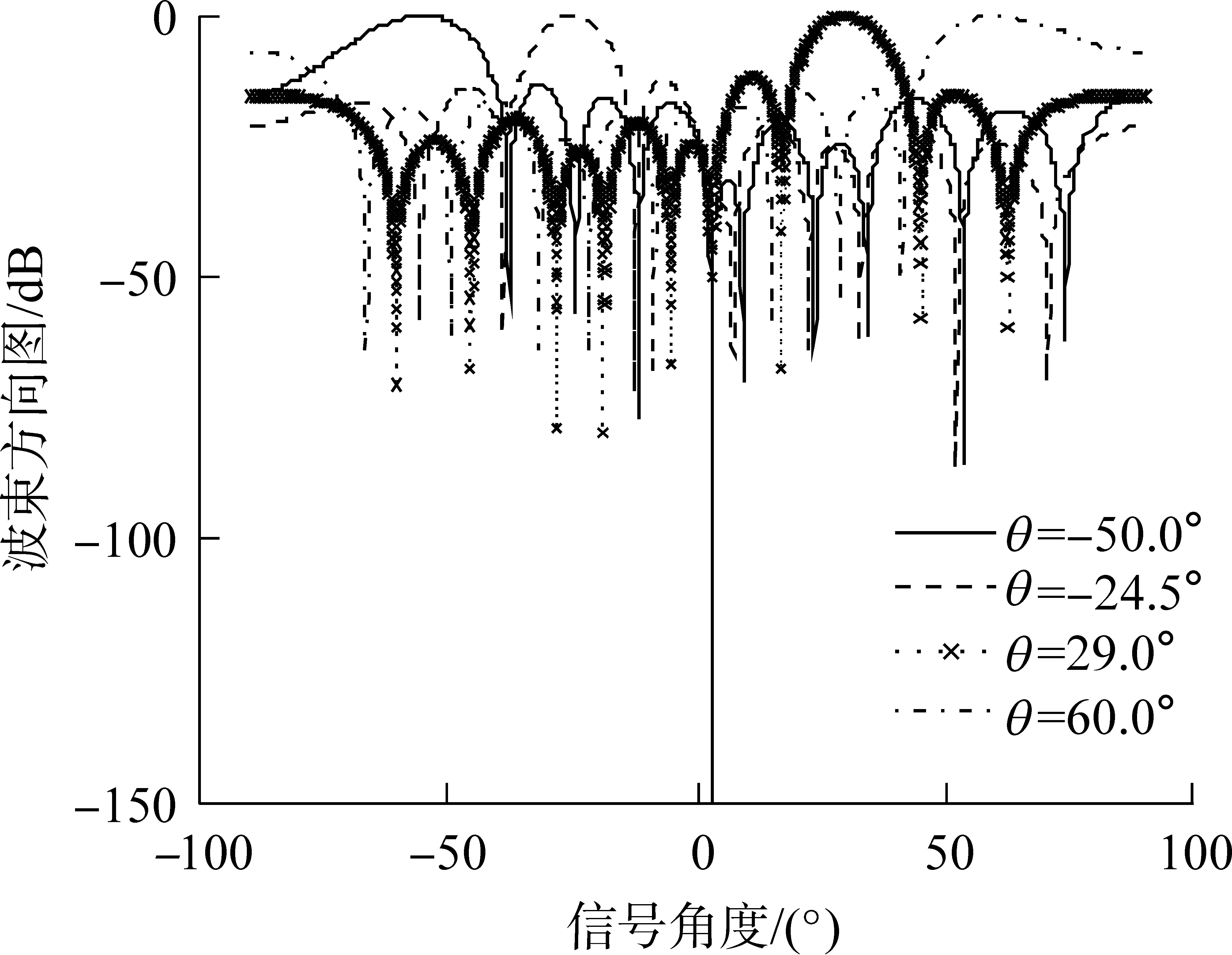
图4 多目标调零天线在不同入射角时的方向图
Fig.4Patternsofmultiple-objectsnullingantennainthediffe-rentincidenceangles
4.2 输出SINR仿真
首先假设阵列干扰信号不变,4个卫星信号的入射角不变.观察60.0°入射的期望信号的阵列增益,该卫星信号的SNR变化范围定义为-30~-10 dB,其他3个卫星信号的SNR保持为-10 dB.理想情况、传统调零天线、带指向约束的多目标调零天线和相控阵天线的输出信干噪比仿真结果如图5(a)所示.理想情况指干扰和其他卫星信号完全被抑制,根据阵列增益的定义,其值为
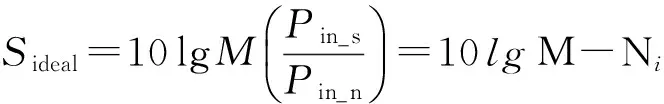
式中,Ni为接收信号的信噪比.
从图5(a)可以看出,输出SINR与输入SNR正好成一次函数关系,但多目标调零天线明显比传统调零天线更接近理想情况.这是由于多目标调零天线抑制了其他卫星信号,同时主瓣的存在也提高了期望卫星信号的增益.由于DMI算法需要估计协方差矩阵,故快拍数K对阵列输出SINR存在明显的影响.
假设4个卫星信号的SNR均为-10dB,其他条件不变,改变快拍数K,观察60.0°入射的期望信号的输出SINR,如图5(b)所示.从图5(b)中可以看出,随着快拍数K的增加,传统调零天线的输出SINR逐渐增加,并趋于平稳,而多目标调零天线的输出SINR始终保持稳定,并比传统调零天线的输出SINR要高.在快拍数较小时,由于传统调零天线的权值没有收敛,故输出SINR较低.由于相控阵天线不具备抗干扰能力,故当干扰从相控阵旁瓣入射时,输出SINR会很低.
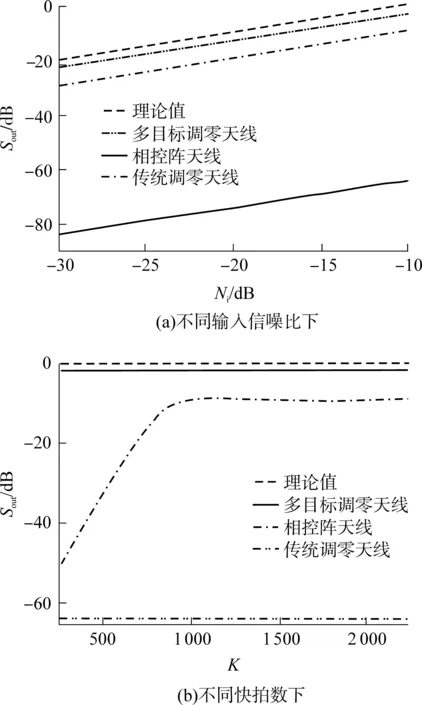
图5 不同天线的输出SINR
Fig.5OutputSINRofdifferentantennas
4.3 入射角度误差仿真
在卫星导航接收机应用中,信号方向一般随接收机和轨道上高速运动的卫星不断变化,可以通过星厉或者其他方法得到卫星角度信息,但很可能存在误差.文中通过指向角度误差与波束方向图和输出SINR的关系来粗略研究指向角度误差的影响.
假设阵列干扰信号不变.采用带指向约束的多目标调零天线观察29.0°入射的期望信号在角度偏差(Δθ)分别为0°、5°、14°时的波束方向图,结果如图6所示.由图可以看出:随着角度偏差的增加,主瓣指向偏离了期望信号方向,期望信号29.0°方向的增益下降;在角度偏差为14°时,方向图会在信号主瓣方向产生零陷,此时期望信号被视为干扰信号而被抑制掉.
当角度偏差在0°~20°范围内变化时,带指向约束的多目标调零天线的输出SINR与无指向误差时的输出SINR之差(ΔSout)如图7所示.由图可以看出:随着角度偏差的不断增大,由于29.0°方向的期望信号被抑制,输出SINR会逐渐降低,即ΔSout逐渐增加;当角度偏差为14.6°时,由于期望信号被抑制,输出ΔSout的误差达到最大值;随着角度偏差的进一步增大,受60.0°方向干扰信号的影响,29.0°方向的期望信号无法被抑制,故此时的输出SINR有所提高.因此,较小的角度误差是可以接受的,但不能太大.
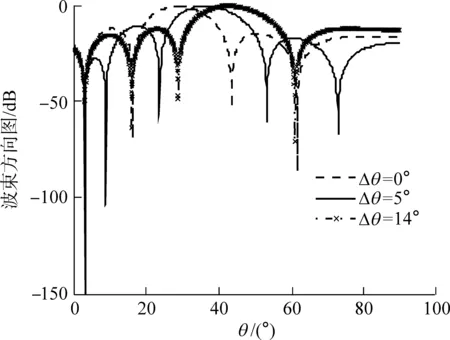
图6 不同角度偏差下的波束方向图
Fig.6Beamformingpatternsindifferentangulardeviation
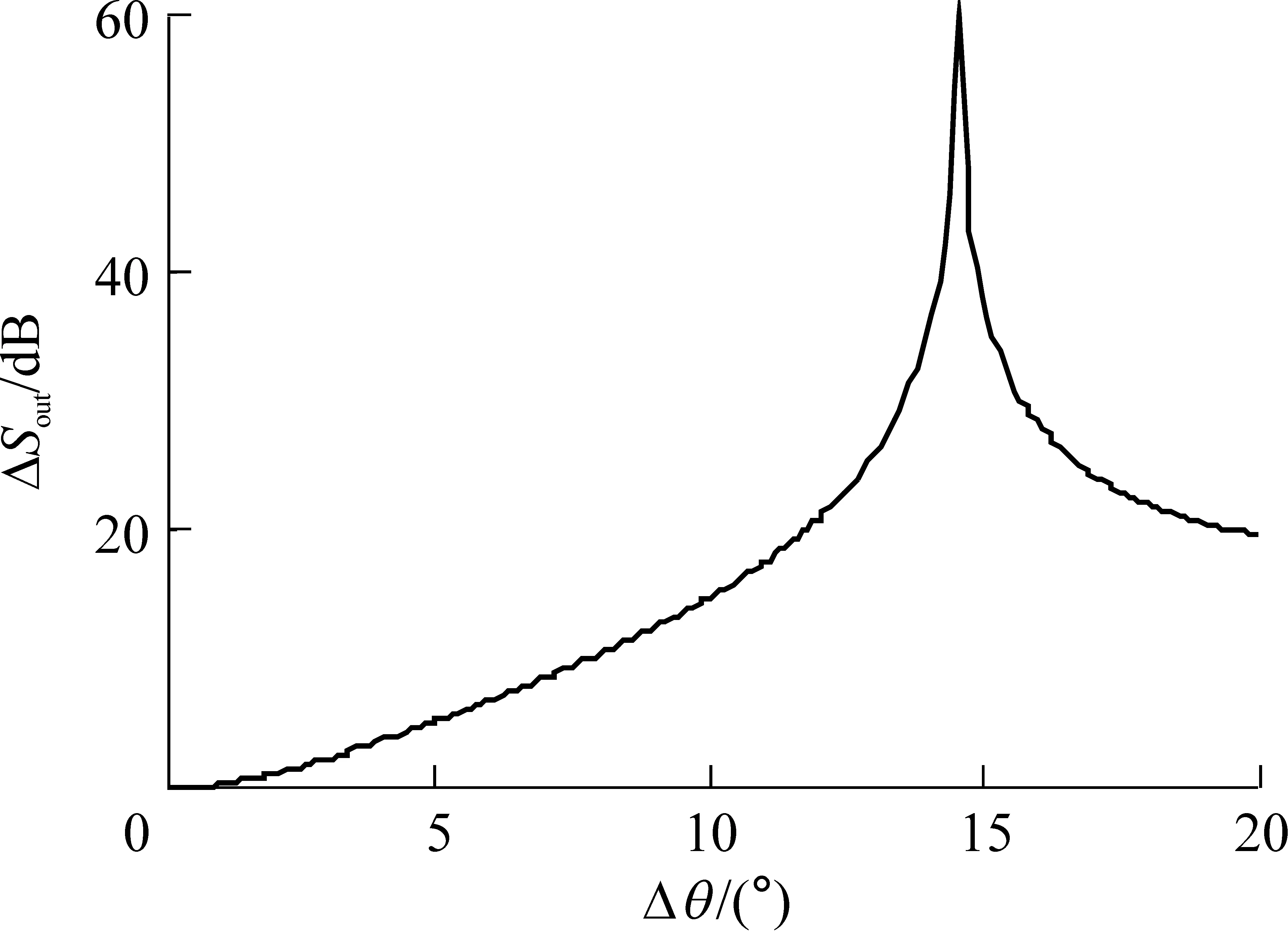
图7 不同角度偏差下的输出信干噪比
Fig.7OutputSINRindifferentangulardeviation
5 结论
采用带指向约束的多目标调零天线,不仅对干扰和其他卫星信号进行了有效的抑制,同时在每个卫星信号入射角度方向形成了主瓣,相比于传统调零天线,大大提高了卫星信号的阵列输出SINR.由于文中算法会对多个目标信号进行波束合成,故系统复杂度增加,数字信号处理器所需的资源会增加3倍.
[1]HANG,DUB,WUW,etal.Anovelhybridphasedarrayantennaforsatellitecommunicationon-the-moveinKu-band[J].IEEETransactionsonAntennasandPropagation,2015,63(4):1375-1382.
[2]YUANY,WANGB,WUUNIFIEDB.Modulationanddemodulationdesignforsatellitecommunicationsystems[J].ElectronicsLetters,2016,52(4):327-329.
[3]RAOJBL,MITELR,PATELDP,etal.Low-costmultibeamphasedarrayantennaforcommunicationswithGEOsatellites[J].IEEEAerospaceandElectronicSystemsMagazine,2013,28(6):122-126.
[4]COMPTONRT.Thepowerinversionadaptivearray:conceptandperformance[J].IEEETransactionsonAerospaceandElectronicSystems,1979,15(6):803-814.
[5]NGAIEC,BLEJERDJ,TRIPhuong,etal.Anti-jamperformanceofsmallGPSpolarimetricarrays[J].IEEEAntennasandPropagationSocietyInternationalSymposium,2002,2(2):128-131.
[6]ZENGHao,AHMADZS,DONGTao,etal.Nullsteeringantennabeamformingutilizingspace-timeadaptiveprocessing[J].JournalofChinaUniversitiesofPostsandTelecommunications,2015,22(4):51-55.
[7]XUJ,LIAOG,ZHUS,etal.ResponsevectorconstrainedrobustLCMVbeamformingbasedonsemidefiniteprogramming[J].IEEETransactionsonSignalProcessing,2015,63(21):1215-1219.
[8]BHOTTOMZA,BAJICIV.ConstantmodulusblindadaptivebeamformingbasedonunscentedKalmanfiltering[J].IEEESignalProcessingLetters,2015,22(4):474-478.[9]ZHITian,BELLKL,vanTREESHL.ArecursiveleastsquaresimplementationforLCMPbeamformingunderquadraticconstraint[J].IEEETransactionsonSignalProcessing,2001,49(6):1138-1145.
[10] HADAD E,MARQUARDT D,DOCLO S,et al.Theoretical analysis of binaural transfer function MVDR beamformers with interference cue preservation constraints[J].IEEE/ACM Transactions on Audio Speech and Language Processing,2015,23(12):2449-2464.
[11] HADAD E,DOCLO S,GANNOT S.The binaural LCMV beamformer and its performance analysis [J].IEEE/ACM Transactions on Audio Speech and Language Processing,2016,24(3):543-558.
[12] RAZAVI S M,RATNARAJAH T.Adaptive LS and MMSE based beamformer design for multiuser MIMO interference channels [J].IEEE Transactions on Vehicular Technology,2016,65(1):132-144.[13] CHANG C P,LIU C W.Unit commitment by lagrangian relaxation and genetic algorithms [J].IEEE Transactions on Power Systems,2000,15(2):707-714.
[14] MEHER P K.Unconstrained hartley domain least mean square adaptive filter [J].IEEE Transactions on Circuits and Systems II:Analog and Digital Signal Processing,1993,40(9):582-585.
[15] BHOTTO M Z A.Robust recursive least-squares adaptive-filtering algorithm for impulsive-noise environments [J].IEEE Signal Processing Letters,2011,18(3):185-188.
[16] ANU Y,WAX M.Performance analysis of the minimum variance beamformer [J].IEEE Transactions on Signal Processing,2015,44(4):928-937.
Multiple-Objects Nulling Antenna with Directional Constraint
ZENGHao1,2ZHOUJian-wen1WANGQiu-shi1WANGHong-liang1HEHai-dan2
(1. College of Communication Engineering, Chongqing University, Chongqing 400044, China;2. Southwest Electronic Technology Research Institute, Chengdu 610036, Sichuan, China)
In satellite navigation receivers, traditional nulling antennas cannot form the main lobe of satellite signal points. In order to form a plurality of main lobes of an antenna corresponding to different satellite signals and thus to improve array gains, an orientation constraint condition is introduced into this paper, and direct matrix inversion is adopted to solve the optimal weight vectors of each satellite signal. Moreover, a beamforming is completed. Then, the computation amount of the proposed algorithm is discussed, and an analytical expression of the array gains is proposed. It is found that this algorithm not only suppresses the external disturbance but also overcomes the mutual interference between satellite signals, and it causes the main lobes of each satellite signal to form, thus improving output SNR. In addition, the effectiveness of the proposed algorithm is demonstrated by the simulation results of pattern and output SINR.
antenna arrays; interference suppression; optimization
1000-565X(2017)01- 0053- 06
2016- 04- 11
重庆市自然科学基金重点资助项目(cstc2013JJB40005);重庆大学中央高校基本科研业务费专项资金资助项目(106112016CDJZR165508)
Foundation item: Supported by the Key Project of the Natural Science Foundation of Chongqing(cstc2013jjb40005)
曾浩(1977-),男,教授,主要从事抗干扰通信技术研究.E-mail:haoz@cqu.edu.cn
TN 928
10.3969/j.issn.1000-565X.2017.01.008

