基于阈值改进Contourlet变换的图像融合算法*

吴鹏 李雯霖,2 齐德昱 宋文龙

(1. 东北林业大学 机电工程学院, 黑龙江 哈尔滨 150040; 2. 华南理工大学 计算机科学与工程学院, 广东 广州 510640)

基于阈值改进Contourlet变换的图像融合算法*

吴鹏1李雯霖1,2齐德昱2†宋文龙1

(1. 东北林业大学 机电工程学院, 黑龙江 哈尔滨 150040; 2. 华南理工大学 计算机科学与工程学院, 广东 广州 510640)

为获得到效果更好的融合图像,提出了一种基于结构相似度(SSIM)阈值自适应判定融合规则的改进算法.该算法对低频子带采用了基于相关系数离均差的加权求和融合算法,以保留更多的概貌信息;对高频子带则先计算待融合图像各个区域的SSIM,然后取平均值作为阈值,再根据各个区域的SSIM与阈值的关系自适应地选择高频子带融合算法,以保留更多的细节信息.实验结果表明,文中改进的图像融合算法可以获得细节更丰富和边缘更清晰的融合图像,融合图像质量的客观评价指标更优.

图像融合;Contourlet变换;结构相似度

图像融合技术能依据需求、利用不同算法对源自同一目标的由不同传感器得到的图像信息进行整合[1],得到冗余度小、可靠性高、信息利用率高的图像[2].在图像融合的多分辨率分析方法中,小波变换因其良好的时频分析特性而成为研究热点[3-4].但由于小波基为不同尺寸的正方形,当分辨率精细程度增加时,正方形尺寸变小最终成“点”来逼近奇异性曲线;水平、垂直、对角方向是一维小波在推广到高维时张成的3个各向同性的方向,这种可分离的小波不能稀疏地表示含线或面的奇异性的高维函数[5- 6].随着多尺度变换技术的发展,人们提出了以Ridgelet[7]、Curvelet[8]为代表的多分辨率分析算法.在此研究基础上,Do等[9]提出的Contourlet变换继承了曲线波(Curvelet)变换的各向异性,是一种“真正的”二维表示方法,它使用“长条形”基灵活多变地逼近曲线,改善了小波变换只有3个方向的基的缺陷,在每个尺度均能提供数目不同、方向灵活的基,产生更多方向的频率子带,通过高维表示更有效地挖掘图像的边缘细节信息,捕捉几何结构,从而迅速成为图像融合界的新宠.

为获得效果更好的融合图像,文中设计了一种基于结构相似度判定融合规则的Contourlet变换,并用于左、右聚焦图像的融合;对Contourlet变换得到低频子带的融合法则进行改进,设计了基于相关系数(CC)离均差(SS)的低频子带加权融合算法,以保留更多的图像概貌信息;计算待融合图像各个区域的SSIM,取平均值作为阈值,再根据各个区域的SSIM与阈值的关系自适应地选择两幅图像对应像素点取平均(AVG)或者边缘信息取最大(EIN)的高频子带融合算法,以保留高频子带更多的细节信息;最后采用基于区域的加权平均(RAVE)融合算法和EIN法进行对比实验.

1 Contourlet变换

Contourlet变换基于Curvelet思想,由拉普拉斯塔形滤波器组(LP)变换[10]和方向滤波器组(DFB)变换分别独立构成,多尺度分析以捕获奇异点[11],多方向分析将方向一致的断点连线形成基本轮廓段,实现完全重构[12].

如图1所示,LP分解能产生一个下采样低通部分b和差值图像a,避免了混频现象的发生.图中,H为分解滤波器,M为采样矩阵,G为合成滤波器.这种处理可循环,进而形成第n层低通部分和高频细节部分,并得到相应低频和高频的子带系数,完成金字塔式图像分解.

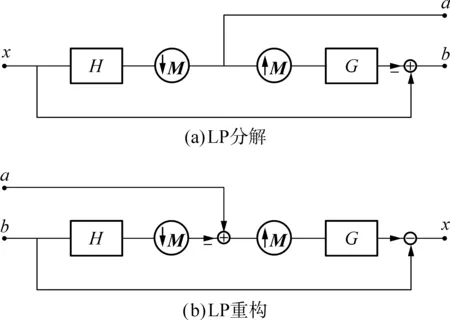
图1 LP分解与重构示意图

Fig.1 Schematic diagram of LP decomposition and reconstruction

这一过程用内积形式表示为

sj=〈x,ψj〉

(1)

Bamberger等[13]构建了可按方向分解图像的DFB,Do[9]等在此基础上做了改进,将分解图像的方式改为经过3次分解后,再对高频子带进行DFB分解,得到的二维(2D)多层频谱划分如图2所示,其中ω1、ω2分别为水平、垂直方向上的频率.

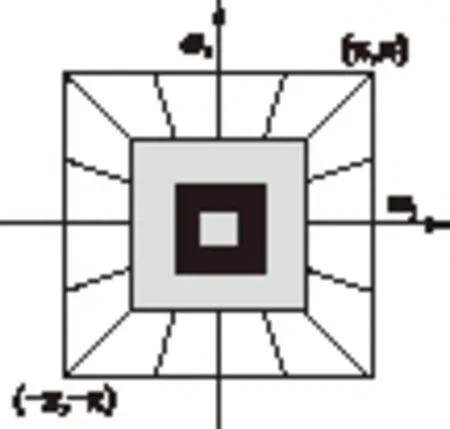
图2 二维多层频谱的划分

用内积形式表示DFB过程：

td=〈x,φd〉

(2)

Contourlet变换的具体过程如图3所示[14].

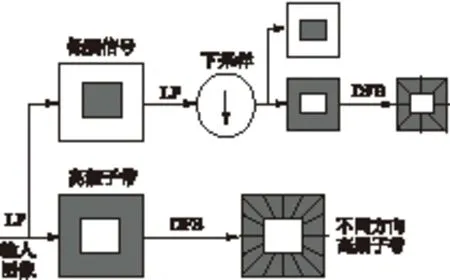
图3 Contourlet变换过程

同样地,用内积形式表示Contourlet变换,根据式(1)、(2),则有

Cj,d=〈sj,φd〉=〈〈x,ψj〉,φd〉=〈x,βj,d〉

(3)

式中,βj,d为Contourlet变换系数空间RM×N的基,βj,d=〈ψj,φd〉. 对均匀分布且对称度高的Zoneplate图像使用Contourlet变换进行3级分解,结果如图4所示,第1级分解得到4个方向子带,第2级分解得到8个方向子带,最细致的第3级分解得到16个方向子带.Contourlet变换可以根据图像特征以及工程需求选择在每一尺度上需要分解的子带数目,细致地展现方向细节特征.Contourlet变换结合了LP有效分解图像低频、高频信息并处理低频信息的优点,以及DFB处理高频信息的优点,这种双滤波器组在空域、频域均具有较完备的表现,能更为稀疏地表示图像细节特征和纹理信息.

2 图像融合

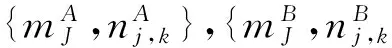
2.1 改进的低频融合规则

低频信息反映了图像的概貌,是反映图像轮廓的绝对性因素.而在Contourlet变换中,多次分解将导致低频子图像成倍缩小,尽可能多地保留图像A、B的低频信息，有助于提高图像质量.

文中提出了基于相关系数(CC)离均差(SS)的低频子带加权融合算法,该算法根据待融合图像的相关性合理地保留图像的概貌信息.

待融合图像A、B的相关函数CAB表示为

(4)

低频信息融合规则为

(5)

式中,wA、wB为改进的基于相关匹配度CAB的权值,

(6)

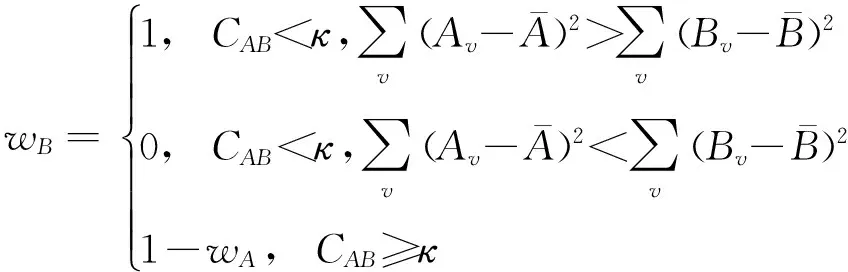
(7)

文中改进了低频信息的融合规则,增加了基于相关系数的阈值判断,当CAB小于判定阈值κ时,表明图像A、B相差较大,引用离均差判定图像区域偏离均值的大小,偏差较大的图像融合系数取0,偏差较小的图像融合系数取1.低频信息能表达图像的概貌,因此匹配相对不剧烈的区域能达到较好的效果.当CAB不小于判定阈值时,表明图像A、B相似度较高,取与κ相关的权值.多次仿真实验发现,κ取0.7时得到的仿真效果最好,故实验中设定κ=0.7.

2.2 改进的高频融合规则

高频信息承载着表现图像细节特性(物体边缘、纹理)的任务[15].这些细节特征融合结果的好坏直接影响了图像的质量,如何更好地保留高频子带信息以减少图像失真一直是Contourlet融合的重点研究方向.Wang等[16]提出了利用图像区域中的亮度、对比度及结构信息定量评价图像质量的方法.文中首先计算待融合图像的结构相似性(SSIM),将其作为高频信息融合算法的选择参数.

设待融合图像A、B的结构相似度为

S(A,B)=[l(A,B)]α[c(A,B)]β[s(A,B)]γ

(8)

(9)

图像A、B越相似,则S(A,B)值越接近于1,这种根据均值方差和协方差评估相似性的算法更符合人眼对影像品质的判断.

图5给出了男人图像的分析结果,其中根据左、右聚焦图像计算得到的SSIM图的图像矩阵由其SSIM值构成,越白的图像区域表示相似度越大,SSIM值越大且越接近于1,越黑的图像区域表示相似度越小,SSIM值越小,直观地表示了原图像A、B的结构相似度;SSIM图的直方图反映了A、B图像的结构相似度SSIM的数值分布情况.计算得到左、右聚焦图像的平均结构相似度为0.927 3.平均结构相似度将原图像结构相似度的数值分布分成两部分,文中令Sth为平均结构相似度的值.根据图5可知,平均结构相似度能够清晰反映不同区域相似度的数值分布.文中引入SSIM判定改进高频区域融合算法,对阈值Sth左、右侧部分对应的原图像区域的高频子带分别采取不同的融合策略,以获得更佳的融合效果.

图5 男人图像的实验结果

首先对图像进行分区,然后计算局部区域的结构相似度.当原图像A、B对应的大小为N×N计算视窗区域内SSIM大于阈值Sth时,表示两者相应区域的相似度比较高.为减少算法耗时,文中选取两幅图像对应像素点取平均(AVG)的融合法则,即

(10)

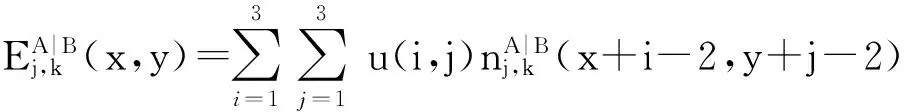
(11)

高频信息融合规则为

(12)

文中改进算法的过程如图6所示.该算法通过针对高、低频子带使用不同的融合法则来得到较优的融合图像.

3 实验

使用Matlab2102a在64位Windows7上进行实验.根据多次实验结果,当Contourlet分解选用塔式分解滤波器“9-7”、方向子带分解滤波器选用“pkva”时有比较好的融合效果.C1、C2是为避免分母为0而设置的常数,计算SSIM值时取C1=(K1l)2、C2=(K2l)2.设定调整因子远小于1,取K=[K1,K2]=[0.02,0.03],默认动态范围L=255.选取局部性视窗为3×3的小区块,通过以像素点为单位平移方形窗口可得到位于窗口内的A、B图像区域的结构相似性指标,直到计算所有位置的局部结构相似性指标为止,最后将所有的局部结构度量的平均值作为阈值Sth.将局部结构相似性值与阈值进行比较,根据规则(10)或者(12)进行融合,得到融合图像.

图6 文中算法过程图

低频信息融合采用经典的基于区域的加权平均(RAVE)融合算法作为对比算法,该算法考虑了邻域像素的值及像素点的关联性,并用加权算法合理地融合.

(13)

高频信息融合采用EIN算法与文中基于SSIM的EIN阈值算法作对比.图7给出了杂物图实验结果.由图中可知,首先分别对右聚焦图与左聚焦图进行Contourlet变换,得到高频系数和低频系数.文中使用3级Contourlet变换可分解得到16个不同方向的系数.分解得到的低频系数按照式(5)-(7)计算,得到融合所需低频信息.由图7(b)与图7(c)计算结构相似度所得SSIM图如图7(f)所示,是高频系数融合判定的索引图.对图像的结构相似度值取平均得到Sth=0.944 7,如图7(d)所示.由SSIM值与阈值的大小关系,得到对应位置的SSIM值的直观显示,见图7(e),然后算法进行融合规则的判定,以尽可能多地保留高频特征信息为原则.对比图7(g)、7(h)可知,图7(h)细节更丰富,如闹钟的指针刻度盘更清晰,书的页面以及边缘也更清楚且物体边缘的明显程度优于相对细节模糊的图7(g).

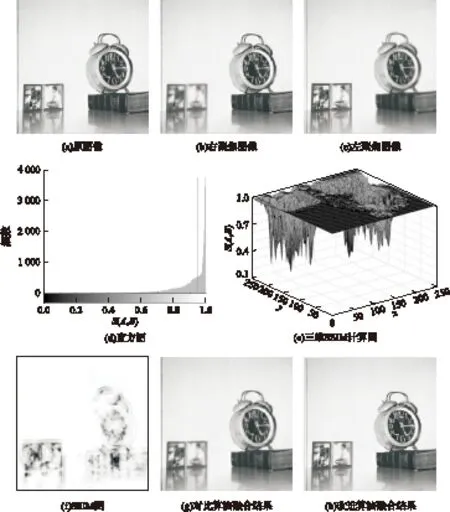
图7 杂物图实验结果

图8给出了夫妇照片的实验结果.由右聚焦图像和左聚焦图像计算得到的SSIM图如图8(f)所示,计算平均SSIM得到阈值Sth=0.940 0,如图8(d)所示,相应的三维SSIM值分布图见图8(e).对比图8(g)和8(h)可知,图8(h)的窗帘褶皱更加精细,花束的轮廓更加清晰，夫妇的神态活灵活现,家具陈设(如沙发、桌子)与周围物体的分界线更明显.这表明,文中改进的融合方法得到的融合图像效果更好.

为客观评价文中图像融合算法的性能,文中利用熵(E)、平均梯度(AG)、峰值信噪比(PSNR)及信噪比(SNR)计算两幅图像的融合效果,结果如表1所示.熵作为体现图像信息量大小的依据,是正相关于信息量丰富程度的.平均梯度反映图像清晰度,其数值与图像层次、清晰程度正相关.峰值信噪比、信噪比也与融合效果正相关.从表1可知,文中改进算法对两幅融合图像的熵、平均梯度、峰值信噪比及信噪比的值均高于对比算法,这表明改进算法的融合效果优于对比算法,融合图像所含的信息量更大,信息的层次更丰富,清晰度更高,与主观判断所得结果一致.

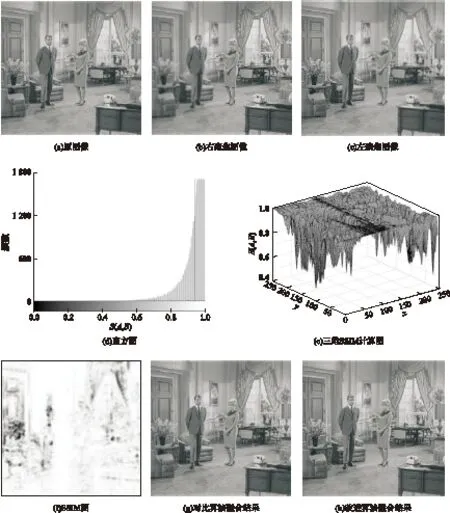
图8 夫妇图实验结果

图名算法EAGSNRPSNR杂物对比算法6.715.5413.1233.56改进算法6.736.7513.5037.39夫妇对比算法7.195.8912.6432.34改进算法7.237.8812.7833.69

4 结论

融合规则对融合效果起着至关重要的作用,为获得效果更好的融合图像,文中改进了融合规则,对包含概貌信息的低频子带采用了基于相关系数的加权求和规则以保留更多的信息,对包含细节信息的高频子带则根据SSIM自适应地选择两幅图像对应像素点取平均或边缘信息取最大的融合规则.实验结果表明,采用文中改进融合规则的算法获得了细节纹理特征更丰富的融合图像,且其客观评判指标结果更优.

[1] 邢涛,李军,王冠勇,等.基于非均匀快速傅里叶变换的SAR方位向运动补偿算法 [J].电子与信息学报,2014,36(5):1023-1029.

XING Tao,LI Jun,WANG Guan-yong,et al.An along-track motion compensation algorithm based on non-uniform fast Fourier transform(NUFFT) for SAR [J].Journal of Electronics & Information Technology,2014,36(5):1023-1029.

[2] HASSAINIA F,MAGANA I,LANGEVIN F,et al.Image fusion by an orthogonal wavelet transform and comparison with other methods [C]∥Proceedings of the 14th Annual International Conference of the IEEE Engineering in Me-dicine and Biology Society.Paris:IEEE,1992:1246-1247.

[3] PERTUZ S,PUIG D,GARCIA M A,et al.Generation of all-in-focus images by noise-robust selective fusion of li-mited depth of field images [J].IEEE Transactions on Image Processing,2013,22(3):1242-1251.

[4] ANDEREAS E,CARLA P L,EDUARDO A B.Multiscale image fusion using the undecimated wavelet transform with spectral factorization and nonorthogonal filter banks [J].IEEE Transactions on Image Processing,2013,22(3):1005-1017.

[5] 李晖晖,郭雷,刘航.基于二代Curvelet变换的图像融合研究 [J].光学学报,2006,26(5):657- 662.

LI Hui-hui,GUO Lei,LIU Hang.Research on image fusion based on the second generation curvelet transform [J].Acta Optica Sinica,2006,26(5):657- 662.

[6] JIAO Li-cheng,TAN Shan.Development and prospect of image multiscale geometric analysis [J].Acta Electronica Sinica,2003,31(12A):1975-1981.

[9] DO M N,VETTERLI M.The contourlet transform:an efficient di-rectional multiresolution image representation [J].IEEE Transactions on Image Processing,2005,14(12):2091- 2106.

[10] WEYRICH N,WARHOLA G T.Wavelet shrinkage and generalized cross validation for image denoising [J].IEEE Transactions on Image Proceeding,1998,7(1):82-90.

[11] 吴一全,殷骏,戴一冕.基于人工蜂群优化的 NSCT 域图像模糊集增强方法 [J].华南理工大学学报(自然科学版),2015,43(1):59- 65.

WU Yi-quan,YIN Jun,DAI Yi-mian.Image enhancement in NSCT domain based on fuzzy sets and artificial bee colony optimization [J].Journal of South China University of Technology(Natural Science Edition),2015,43(1):59- 65.[12] YANG Liu,GUO Bao-long,NI Wei.Multifocus image fusion algorithm based on contourlet decomposition and region statistics [C]∥Proceedings of the 4th International Conference on Image and Graphics.Chengdu:IEEE,2007:707-712.[13] BAMBERGER R H,SMITH M J T.A filter bank for the directional decomposition of images:theory and design [J].IEEE Transactions on Signal Processing,1992,40(4):882- 893.

[14] FENG P,PAN Y,WEI B,et al.Enhancing retinal image by the Contourlet transform [J].Pattern Recognition Letters,2007,28(4):516-522.

[15] 殷明,庞纪勇,魏远远,等.结合 NSDTCT 和稀疏表示的遥感图像融合 [J].光子学报,2016,45(1):10-17.

YIN Ming,PANG Ji-yong,WEI Yuan-yuan,et al.Remote sensing image fusion based on non-subsampled dual-tree complex contourlet transform and sparse representation [J].Acta Photonica Snica,2016,45(1):10-17.

[16] WANG Z,BOVIK A C,SHEIKH H R,et al.Image quality assessment:from error visibility to structural similarity [J].IEEE Transactions on Image Processing,2004,13(4):600- 612.

An Image Fusion Algorithm Based on Threshold-Improved Contourlet Transform

WUPeng1LIWen-lin1,2QIDe-yu2SONGWen-long1

(1. College of Mechanical and Electrical Engineering, Northeast Forest University, Harbin 150040, Heilongjiang, China;2. School of Computer Science and Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China)

In order to obtain better fusion images, an improved algorithm on the basis of structural similarity (SSIM) threshold is proposed to determine fusion rules adaptively. In the algorithm, for low frequency sub-bands, a weighting summation fusion algorithm on the basis of correlation coefficient and deviation from mean is adopted to preserve more general information. For high frequency sub-bands, the SSIM of each region of the image to be fused is calculated first and then the corresponding average value is taken as the threshold. Afterwards, a high frequency sub-band fusion algorithm is selected adaptively according to the relationship between the SSIM of each region and the threshold, so as to retain more detail information. Experimental results show that the improved image fusion algorithm helps achieve the fused images of richer detail, sharper edge and better objective evaluation index of quality.

image fusion; Contourlet transform; structural similarity

1000-565X(2017)01- 0035- 07

2016- 04- 01

国家自然科学基金资助项目(31470714);哈尔滨市科技创新人才研究专项(2014RFQXJ127);东北林业大学中央高校基本科研业务费专项资金资助项目(2572014CB14);黑龙江省博士后科研启动基金资助项目(LBH-Q14006)

Foundation item： Supported by the National Natural Science Foundation of China(31470714)

吴鹏(1980-),男,博士,副教授,主要从事图像处理研究.E-mail:79102570@qq.com

† 通信作者： 齐德昱(1959-),男,教授,博士生导师,主要从事计算机系统结构、人机交互、图像处理算法优化研究.E-mail:qideyu@scut.edu.cn

TP 317.4

10.3969/j.issn.1000-565X.2017.01.005