高考程序框图考查的多种意识

张刚

程序框图是每年高考的常考点，且和高中数学的其他知识交汇命题，考题多以选择题或填空题的形式出现，难度不大。下面就这方面需要强化的几种意识，加以总结，以期能对同学们的学习有所启发和帮助。

一、不等式意識

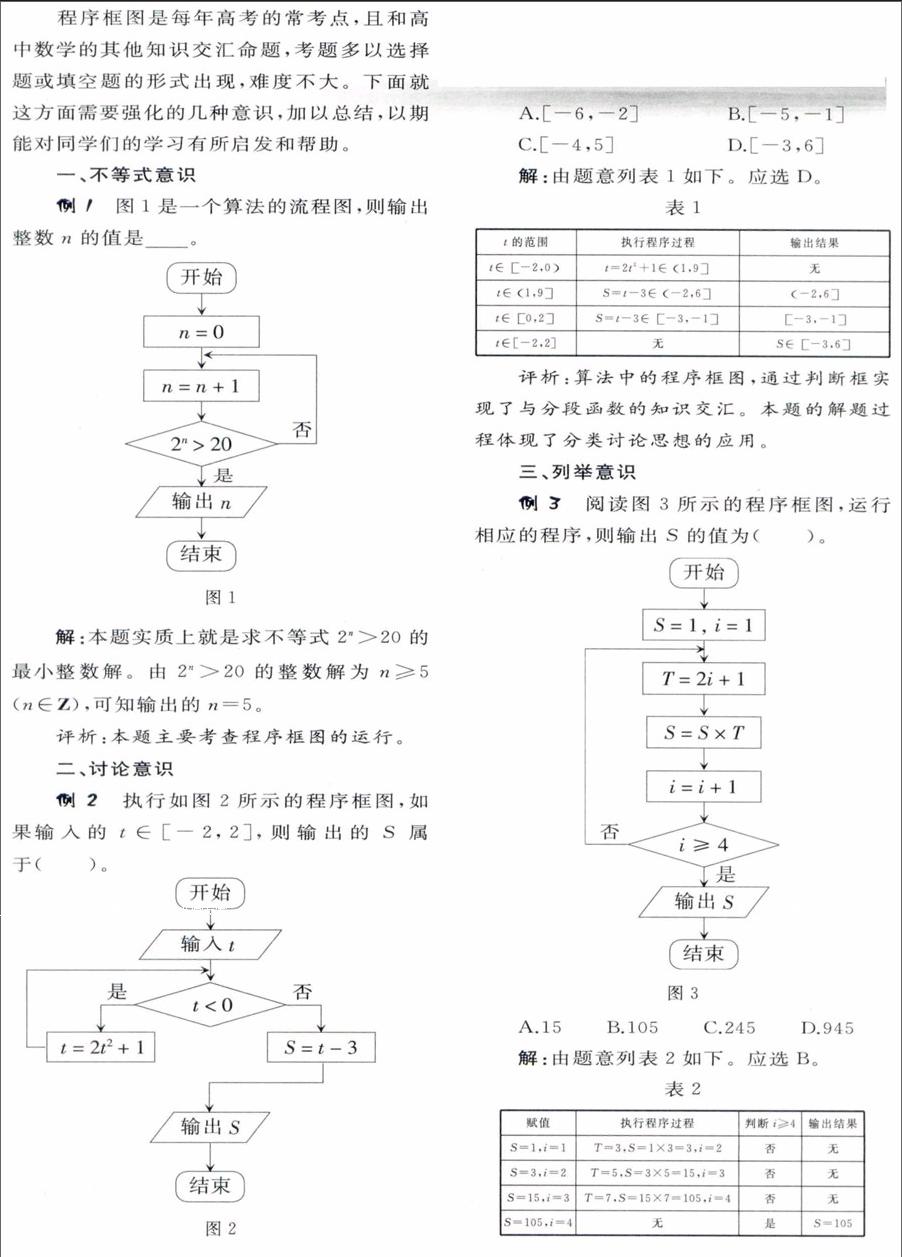
例1 图1是一个算法的流程图，则输出整数n的值是____。

解：本题实质上就是求不等式2ⁿ>20的最小整数解。由2ⁿ>20的整数解为n≥5（n∈z），可知输出的n=5。

评析：本题主要考查程序框图的运行。

二、讨论意识

例2 执行如图2所示的程序框图，如果输入的t∈[-2，2]，则输出的S属于（ ）。

A.[-6，-2] B.[-5，-1]

C.[-4，5] D.[-3，6]

解：由题意列表1如下。应选D。

评析：算法中的程序框图，通过判断框实现了与分段函数的知识交汇。本题的解题过程体现了分类讨论思想的应用。

三、列举意识

例3 阅读图3所示的程序框图，运行相应的程序，则输出S的值为（ ）。

A.15 B.105 C.245 D.945

解：由题意列表2如下。应选B。

评析：程序框图主要是由赋值框和条件框组成的。注意条件框中的判断条件，在运行程序时要将执行的结果逐个列举，直至程序结束。

四、累乘（加）意识

例4 m=7，n=3时，执行如图4所示的程序框图，则输出的S值为（ ）。

A.7 B.42 C.210 D.840

解：由题意列表3如下。应选C。

评析：题中执行S=S×k是累乘化简的关键依据。解题时，要弄清程序退出的条件，要准确运行程序。

五、循环意识

例5 执行如图5所示的程序框图，如果输入的t=0.01，则输出的n=（ ）。

A.5 B.6 C.7 D.8

解：由题意列表4如下。应选C。

评析：准确识别程序框图的循环次数是解答本题的关键。

（责任编辑 郭正华）