开圆形洞口整体墙和小开口整体墙的研究

赵 青 赵 军

(安阳工学院 安阳 455000)

开圆形洞口整体墙和小开口整体墙的研究

赵 青 赵 军

(安阳工学院 安阳 455000)

为了研究开圆形洞口整体墙和小开口整体墙，采用圆形洞口与正方形洞口进行对比分析。分别将圆形洞口等效为边长为直径的正方形、等面积正方形和圆内接正方形对比顶点位移。结合有限元分析和理论分析，采用圆内接正方形作为等效矩形截面，进行惯性矩计算；采用无洞口的横截面面积乘以洞口削弱系数，进行截面面积计算。

圆形洞口；整体墙；小开口整体墙

随着我国经济的迅猛增长，我国居民对住宅建筑的要求不断提高，单一的方形洞口已不能满足人们审美的需要，其他形状洞口的剪力墙成为可能。

根据剪力墙的开洞率对其受力性能的影响分为整体墙（包括小开口整体墙）和联肢墙。整体墙和小开口整体墙整体性较强，破坏首先发生在底层。联肢墙截面的整体性已经破坏，墙体的线刚度比同列两孔间所形成的连梁的线刚度大得多，破坏首先发生在连梁上。圆形洞口所形成的连梁相当于变截面梁，改变了联肢墙的破坏特性，联肢墙不适合设置圆形洞口。因此，研究开圆形洞口的整体墙和小开口墙的位移计算。

1 整体墙和小开口整体剪力墙顶点侧移

在水平荷载作用下，整体墙受力如同竖向悬臂墙，符合平截面假定，正应力为直线规律分布。当整体墙上无洞口时，材料采用弹性变形范围内的小变形特性，按照虚功原理计算，整体墙的顶点侧移包括两部分：弯曲侧移和剪切侧移。当整体墙上有洞口时，洞口对弯曲侧移的影响采用有洞与无洞截面惯性矩沿竖向的加权平均值 ；洞口对剪切侧移的影响采用无洞口的横截面面积乘以洞口削弱系数。

均布荷载作用下，有洞口整体墙考虑弯曲和剪切变形后的顶点位移公式为∶[1]

第一项为弯曲变形对侧移的影响，第二项为剪切变形对侧移的影响。对比无洞口时的公式，仅有惯性矩和截面面积不同。有洞口整体墙的惯性矩采用有洞与无洞截面惯性矩沿竖向的加权平均值：[1]

对于整体墙和小开口墙，剪切对侧移的影响极小，圆形洞口仍可以采用无洞口的横截面面积乘以洞口削弱系数。

各段的开洞部分的惯性矩及相应高度的取值针对的是方形洞口，对于圆形洞口，各段开洞部分的惯性矩采用直径处截面惯性矩或者采用等效正方形洞口时的截面惯性矩，相应高度采用直径或等效正方形边长。

2 有限元分析

2.1 有限元模型

采用ANSYS建立剪力墙试件的有限元模型,对层高为3m的10层双肢对称剪力墙进行计算分析，墙高为6m,墙肢截面厚度均为200mm。试件比例为1∶ 1，在单元左侧作用均布面荷载q=20kN/m2。材料弹性模量为3×104MPa，泊松比为0.2，剪切弹性模量为,1.25×104MPa，剪应力不均匀系数采用1.2。墙体均为整体墙和整体小开口墙，并且洞口居中布置。

对于测序得到的序列信息，首先根据PE reads之间的Overlap关系，将Hiseq测序得到的双端序列数据进行拼接以获得完整的一条序列Tags，同时对Reads的质量和拼接的效果进行质控过滤。之后利用不同软件进行数据分析，如QIIME软件进行OTU划分，基于Silva和UNITE分类学数据库对OTU进行分类学注释分析、利用MEGAN软件分析样品中所有微生物的进化关系和丰度差异，利用Mothur软件对样品进行Alpha多样性指数评估等。

2.2 正方形洞口的边长和顶点位移

选取一组洞口边长为a的正方形洞口，建立有限元模型进行分析，正方形洞口尺寸、顶点位移和开洞率见表1.1。

表1 .1 正方形洞口尺寸、顶点位移和开洞率

2.3 直径为D1的圆形洞口

取圆形洞口的直径D1 与正方形洞口的边长a 相等，圆形洞口直径、顶点位移和开洞率见表1.2。

表1 .2 圆形洞口直径D1、顶点位移和开洞率

2.4 直径为D2的圆形洞口

表1 .3 圆形洞口直径D2、顶点位移和开洞率

2.5 直径为D3的圆形洞口

按照圆形洞口为正方形洞口的外接圆的原则，取洞口的直径D3，洞口尺寸、顶点位移和开洞率见表1.4。

表1 .4圆形洞口直径D3、顶点位移和开洞率

?

2.6 正方形洞口顶点位移有限元值和理论值

对正方形洞口顶点位移的有限元值与理论值对比，见表1.5.

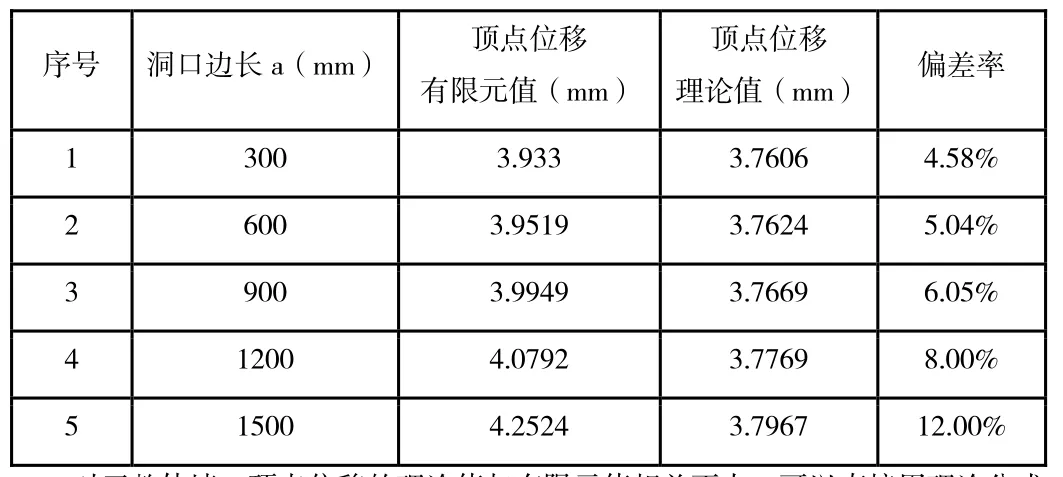
表1 .5 正方形洞口顶点位移有限元值和理论值对比

对于整体墙，顶点位移的理论值与有限元值相差不大，可以直接用理论公式计算，对于小开口整体墙，采用理论值乘以1.2，所得到的等效刚度是保守的。

2.7 正方形洞口与洞口直径为D1、D2、D3圆形洞口的顶点位移对比

分别将正方形洞口的顶点位移与洞口直径为D1、D2、D3的圆形洞口的顶点位移进行对比，见表1.5、表1.6、表1.7，并将顶点位移用图1.1分析。

表1 .5 正方形与直径为D1圆形洞口顶点位移偏差对比

表1 .6 正方形与直径为D2圆形洞口顶点位移偏差对比

表1 .7 正方形与直径为D3圆形洞口顶点位移偏差对比

由上可知，洞口直径为D2的圆形洞口的顶点位移与正方形最接近，即可以按照面积相等的原则，将圆形洞口等效为矩形洞口，然后按照矩形洞口公式进行理论计算。

2.8 圆形洞口顶点位移有限元值和理论值对直径为D2的圆形洞口顶点位移的有限元值与理论值对比，见表1.8。

图1 .1 正方形洞口顶点位移与圆形洞口顶点位移对比

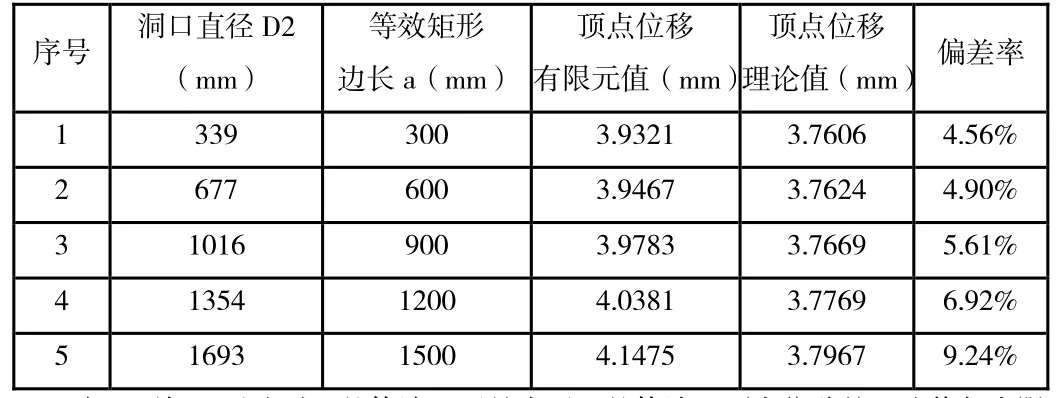
表1 .8 洞口直径为D2圆形洞口的顶点位移有限元值和理论值对比

由上可知，无论对于整体墙，还是小开口整体墙，顶点位移的理论值与有限元值相差不大。主要原因是开圆形洞口的剪力墙的整体性能比开方形洞口的整体性强。

对直径为D3的圆形洞口顶点位移的有限元值与理论值对比，见表1.9。

表1 .9 洞口直径为D3圆形洞口的顶点位移有限元值和理论值对比

由上可知，对于整体墙，顶点位移的理论值与有限元值相差不大，可以直接用理论公式计算，对于小开口整体墙，采用理论值乘以1.2。

3 结论

由图1.1可知：直径为D2圆形洞口的顶点位移与正方形洞口最接近，即采用面积相等的原则得到的等效矩形截面的有限元值最接近。但是，再对矩形截面剪力墙进行有限元分析中，将剪力墙分为整体墙和小开口整体墙，整体墙直接用理论公式计算，对于小开口整体墙，采用理论值乘以1.2。由表1.9可知：直径为D3圆形洞口的顶点位移的有限元值与理论值的偏差不大于20%。因此，对于圆形截面，应采用内接正方形作为等效矩形截面，进行惯性矩Iq计算。对于整体墙直接用理论公式计算，对于小开口整体墙，采用理论值乘以1.2。

[1]包世华，张铜生.高层建筑结构设计和计算[M] .北京：清华大学出版社，2005

[2]江见鲸，陆新征.混凝土结构有限元分析[M] .北京：清华大学出版社，2013

G322

B

1007-6344（2017）01-0246-02

赵青（1977-），女，讲师，安阳工学院土木与建筑工程学院，赵军（1980-），男，讲师，安阳工学院土木与建筑工程学院，