去除移动心电中运动干扰的前馈组合自适应滤波器

张洹千 张树林 杜晓薇 金庆辉 李擎 杨坚 赵建龙†

(1.中国科学院 上海微系统与信息技术研究所， 上海 200050; 2.中国科学院大学， 北京 100049; 3.徐汇区中心医院， 上海 200031)

移动心电信号中的运动干扰会降低心电信号的质量[1]，使其难以被辨认而导致误诊[2].由于运动干扰与移动心电信号的频率类似[3]，很难被去除，为了解决上述问题，通常使用自适应滤波器去除移动心电信号中的运动干扰[4].由Widrow和Hoff等[5]提出的最小均方自适应滤波器(LMS-AF)是最常使用的自适应滤波器，由于其固定步长μ与失调成正比，与收敛速度成反比，因此，传统的LMS-AF在收敛速度和失调上存在矛盾.

通常解决上述矛盾的方法是使用变步长自适应滤波器(VSS-LMS-AF)[6].运算开始时VSS-LMS-AF会使用大的步长来加速算法的收敛速度，步长会随着迭代次数的增加而减小，以保证收敛精度.VSS-LMS-AF可以优化LMS-AF的性能.一些判据可以用来调整步长，例如瞬态均方误差[7]、相邻梯度的符号变化[6]、瞬态均方误差的梯度[8]、误差信号的自相关[9]、误差信号自相关系数的均值[10]、输入信号和误差信号的方差[11]、输入信号和误差信号之间的互相关[12]等.但是VSS-LMS-AF必须改变其步长来跟踪运动干扰的变化，跟踪的延时会增加输出信号的失调[13]，造成信号失真.

有报道称[14]，组合自适应滤波器(C-AF)可以用来减小滤波器的跟踪延时，从而减小信号失真.C-AF将两个自适应滤波器并联，两个自适应滤波器的输出经过组合权重混合后形成最终输出.组合权重由误差信号反馈控制.两个并联自适应滤波器中的第1个具有高收敛精度(HCA-AF)，第2个具有快收敛速度(FCS-AF).但由于C-AF的反馈通路存在延时，会引起滤波器输出失调，造成信号失真.

文中提出了一种前馈组合自适应滤波器(FFC-AF)，用来去除移动心电中的运动干扰，进一步减小滤波器的失真，并提高信号干扰率.

1 方法

1.1 LMS-AF和VSS-LMS-AF的基本情况

如图1所示[15]，LMS-AF使用了一个参考信号X(k)，其与原始信号s(k)没有相关性，与噪声信号n(k)有相关性.

图1 噪声消除应用的自适应滤波器框图Fig.1 Block diagram of adaptive filter for noise cancellation

图1中，d(k)=s(k)+n(k)是输入信号，s(k)是原始信号，n(k)是噪声信号，且与原始信号无关.e(k)是误差信号.y(k)是滤波器的输出，y(k)=WT(k)·X(k)，其中WT(k)是滤波器权重向量的转置，k是迭代次数.

LMS-AF滤波器的权重向量由等式(1)计算得到：

W(k+1)=W(k)+μe(k)X(k)

(1)

式中，μ为LMS-AF的步长.对于VSS-LMS-AF来说，用μ(k)代替μ，且μ(k)随迭代次数k改变.

自适应算法可以调整权重向量W(k)，使得估计误差e(k)的均方值最小化.

这里假设y(k)的均方值近似等于n(k)的均方值，而实际上两者之间存在失调，从而导致信号失真.

LMS-AF滤波器信号输出失调由式(2)计算得到[13]：

(2)

从式(2)可以看出，Mexcess与步长μ成正比，Mlag与步长μ成反比.也就是说，小步长会造成低Mexcess和高Mlag；相反，大步长会造成高Mexcess和低Mlag.

为了维持低的Mtotal，有运动干扰时用一个大步长来减小Mlag，无运动干扰时用一个小步长来减小Mexcess.由于LMS-AF步长固定，不能根据运动干扰改变步长，因此会有一个较大的Mtotal，即有较大信号失真.VSS-LMS-AF可以随运动干扰改变其步长，但其步长变化速度无法跟踪突发的运动干扰.因此，存在突发运动干扰时，会有一个比较大的Mtotal，即有较大信号失真.因此，LMS-AF和VSS-LMS-AF都有较大的信号失真.

1.2 组合自适应滤波器

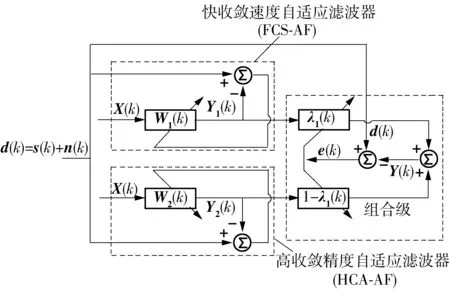
图2 组合自适应滤波器的结构Fig.2 Structure of combined adaptive filter

C-AF的输出可以用下式表示：

(3)

然而，C-AF的组合参数受到误差信号e(k)的反馈通路控制，反馈通路有传播延时，因此组合参数在无运动干扰和有运动干扰切换时存在延时.这个延时会造成失调的增加，增加信号失真，同时降低信号干扰率.

1.3 前馈组合自适应滤波器

为了进一步减小失真，提高滤波器的性能，提出了一种前馈组合自适应滤波器(FFC-AF)，如图3所示.它使用了一条经过参考信号X(k)的前馈通路来控制组合权重参数，而不是使用经过反馈通路的误差信号e(k).参考信号X(k)是从人体采集的电极皮肤接触阻抗信号，具体的采集方法可以参考之前的研究报告[21].

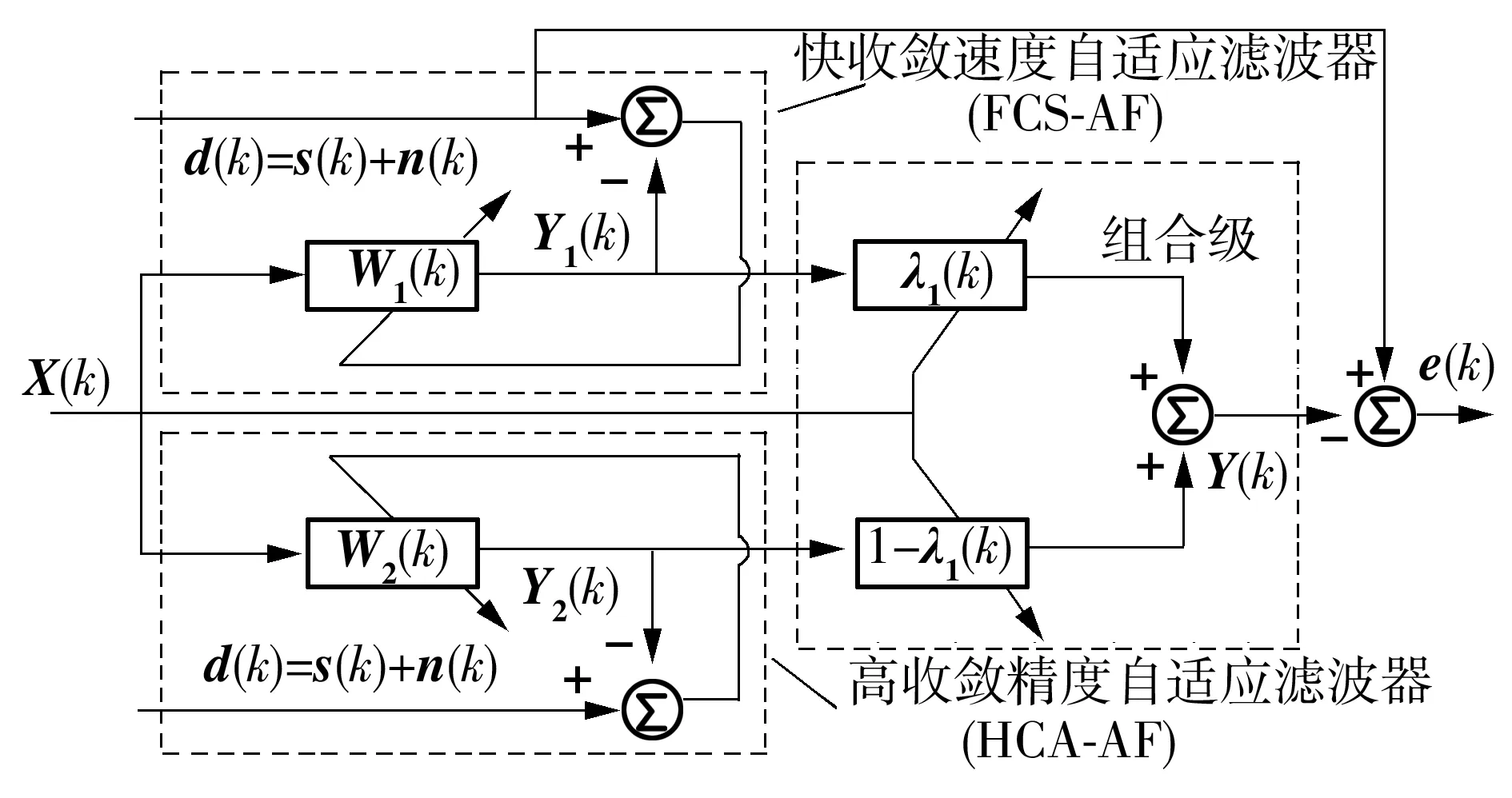
图3 前馈组合自适应滤波器的结构Fig.3 Structure of feed forward combine adaptive filte

无运动干扰情况下，经过参考信号X(k)的前馈通路可以屏蔽误差信号e(k)的变化.有运动干扰情况下，FFC-AF会维持一个小的步长，因此，FFC-AF可以获得比C-AF更小的失真.

图3中滤波器的输出可以用下式表示：

(4)

(5)

δ(k)是参考信号的方差,

(6)

式中，n为参考信号的数据长度.

式(5)中的参数p定义为

(7)

2 计算机仿真和结果分析

使用之前实验中10位健康志愿者的移动心电记录(1143个心动周期)[21]作为原始数据，通过Labview来分析处理数据.

图4中放大显示了有运动干扰的迭代次数为5 000—10 000的情况，可以看出，有运动干扰的情况下：

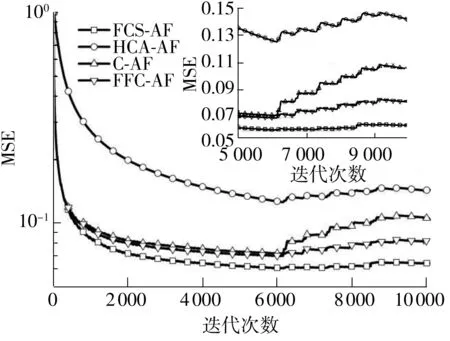
图4 自适应滤波器MSE与迭代次数之间的关系Fig.4 Relation of iteration number and adaptive filters’ MSE

(1)C-AF的MSE位于FCS-AF和HCA-AF的中间,因为C-AF由FCS-AF和HCA-AF的输出经过一个受误差信号的反馈控制的组合参数加权得到;

(2)FFC-AF的MSE位于C-AF和FCS-AF的中间,因为FFC-AF由FCS-AF和HCA-AF的输出经过一个受参考信号的前馈控制的组合参数加权得到,而且前馈控制相比反馈控制对运动干扰信号反应速度更快，因此由前馈控制的FFC-AF相比由反馈控制的C-AF的MSE更小.

为了进一步比较FFC-AF和C-AF的性能，从信号失真和信号干扰率两个方面来比较分析.失真是移动心电信号中去除运动干扰后，与原始信号的相似程度，用无运动干扰的移动心电信号和自适应滤波器输出信号之间的相关性来评估.信号干扰率是自适应滤波器的运动干扰去除效果，用无运动干扰的移动心电信号的方差除以运动干扰的方差来表示.

2.1 信号失真分析

为了比较FFC-AF和C-AF滤波器输出信号的失真度，计算了滤波器输出信号与原始移动心电信号之间的相关性，相关性越高表示失真度越小.计算了705个无运动干扰心动周期的相关性数据，这些无运动干扰的心动周期通过手动选择的方式得到.图5中用散点图的方式概括了相关性的分析结果.表1中统计分析了图5中的数据.10组实验数据的中位数显示两个自适应滤波器输出的相关性系数分别为CorFFC-AF=0.900、CorC-AF=0.871.

结果表明：FFC-AF和C-AF与原始移动心电信号之间的相关系数均大于0.85，说明这两种滤波器的输出信号与原始信号具有良好的相关性，信号失真较小，相比之下，FFC-AF具有更小的信号失真度(相关系数平均值达0.900).

图5 无运动干扰心动周期与自适应滤波器输出之间相关性系数的散点图

Fig.5 Scatter diagrams of correlation between cardiac cycle without motion artifact and adaptive filter output

表1 自适应滤波器的输出与原始心电信号的相关性

Table 1 Correlation between adaptive filter output and original ECG signal

参数相关系数FFC-AF输出C-AF输出数据10.9070.876数据20.9140.870数据30.9200.881数据40.8990.873数据50.8860.856数据60.8840.860数据70.9210.894数据80.9150.890数据90.9160.872数据100.8370.842中位数0.9000.871均方差0.0260.016

2.2 信号干扰率分析

为了比较FFC-AF和C-AF对运动干扰的去除效果，使用信号干扰率(SAR)作为评价指标，即

(8)

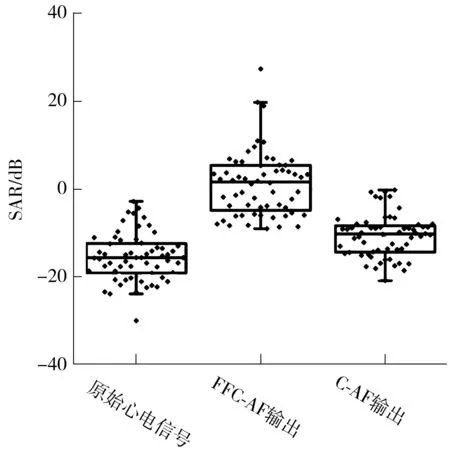
图6 信号干扰率Fig.6 Signal artifact ratio

可以看出FFC-AF的信号干扰率为1.718 dB，C-AF的信号干扰率为-10.174 dB，比原始移动心电信号的信号干扰率(-15.588 dB)均有提高，说明FFC-AF和C-AF均可以有效去除原始信号中的运动干扰.相比之下，FFC-AF具有更高的信号干扰率，比原始移动心电信号的信号干扰率提高了17.306 dB，比C-AF的信号干扰率提高了11.892 dB，可见延时的减小，可以大大提高运动干扰的去除效率.

2.3 滤波参数分析

前文提到式(7)中的参数pnon和psta会对滤波效果产生影响，因此对这两个参数的取值进行了分析.仿真中分别取pnon=40,80,120,160；psta=0.1,1,10,30，并对所有10组数据进行平均，得到图7和8.从图7中可以看出，随着pnon和psta的增加，信号干扰率得到改善.从图8中可以看出，随着pnon和psta的增加，无运动干扰心动周期与自适应滤波器输出之间的相关性降低，说明信号失真度增加.因此，pnon和psta的取值有一个折衷考虑.

图7 参数pnon和psta变化对信号干扰率的影响Fig.7 Effect of parameters pnon and psta versus signal artifact ratio

图8 参数pnon和psta变化对信号相关性的影响Fig.8 Effect of parameters pnon and psta versus correlation

3 结论

文中提出了一种前馈组合自适应滤波器(FFC-AF)，用来去除移动心电信号中的运动干扰.仿真结果表明，利用FFC-AF去除移动心电信号中的运动干扰，输出信号与原始信号的相关性良好，相关性中位值达到0.900，高于C-AF的相关性中位值0.871，说明FFC-AF具有更小的信号失真.FFC-AF具有更高的信号干扰率，比原始移动心电信号的信号干扰率提高了17.306 dB，比C-AF的信号干扰率提高了11.892 dB，说明FFC-AF具有优良的运动干扰去除性能.因此，FFC-AF可用于去除移动心电中的运动干扰.

参考文献：

[1] ROMERO I,BERSET T,BUXI D,et al.Motion artifact reduction in ambulatory ECG monitoring:an integrated system approach [C]∥Proceedings of the 2nd Conference on Wireless Health.San Diego,California:[s.n.],2011:11- 14.

[2] WEBSTER J G.Reducing motion artifacts and interference in biopotential recording [J].IEEE Transactions on Biomedical Engineering,1984,31:823- 826.

[3] THAKOR N V,WEBSTER J G,TOMPKINS W J.Estimation of QRS complex power spectra for design of a QRS filter [J].IEEE Trans Biomed Eng,1984,31:702- 706.

[4] IYER V K,PLOYSONGSANG Y,RAMAMOORTHY P A,Adaptive filtering in biological signal-processing [J].Critical Reviews in Biomedical Engineering,1990,17:531- 584.

[5] WIDROW B,GLOVER J R JR,MCCOOL J M,et al.Adaptive noise cancelling:Principles and applications [J].Proceedings of the IEEE,1975,63:1692- 1716.

[6] HARRIS R,CHABRIES D M,BISHOP F.A variable step(VS) adaptive filter algorithm [J].IEEE Transactions on Acoustics,Speech and Signal Processing,1986,34:309- 316.

[7] KWONG R H,JOHNSTON E W.A variable step size LMS algorithm [J].IEEE Transactions on Signal Processing,1992,40:1633- 1642.

[8] MATHEWS V J,ZHENHUA X.A stochastic gradient adaptive filter with gradient adaptive step size [J].IEEE Transactions on Signal Processing,1993,41:2075- 2087.

[9] ABOULNASR T,MAYYAS K.A robust variable step-size LMS-type algorithm:analysis and simulations [J].IEEE Transactions on Signal Processing,1997,45:631- 639.

[10] WEE-PENG A,FARHANG-BOROUJENY B.A new class of gradient adaptive step-size LMS algorithms [J].IEEE Transactions on Signal Processing,2001,49:805- 810.

[11] GREENBERG J E.Modified LMS algorithms for speech processing with an adaptive noise canceller [J].IEEE Transactions on Speech and Audio Processing,1998,6:338- 351.

[12] SHAN T J,KAILATH T.Adaptive algorithms with an automatic gain control feature [J].IEEE Transactions on Circuits and Systems,1988,35:122- 127.

[13] HAYKIN S.Adaptive filter theory [M].[S.l.]:Prentice-Hall Inc,1996:706- 710.

[14] ARENAS-GARCIA J,FIGUEIRAS-VIDAL A R,SAYED A H.Mean-square performance of a convex combination of two adaptive filters [J].IEEE Transactions on Signal Processing,2006,54:1078- 1090.

[15] DINIZ P S.Adaptive filtering:algorithms and practical implementation [M].[S.l.]:Kluwer Academic Publishers,2002:7- 8.

[16] OSGOUEI S G,GERAVANCHIZADEH M.Speech enhancement using convex combination of fractional least-mean-squares algorithm [C]∥International Symposium on Telecommunications(IST).Tehran:[s.n.],2010:869- 872.

[17] LOPES C G,SATORIUS E H,ESTABROOK P,et al.Adaptive carrier tracking for mars to earth communications during entry,descent,and landing [J].IEEE Transactions on Aerospace and Electronic Systems,2010,46:1865- 1879.

[18] FERRER M,GONZALEZ A,DE DIEGO M,et al.Convex combination filtered-X algorithms for active noise control systems [J].IEEE Transactions on Audio,Speech,and Language Processing,2013,21:156- 167.

[19] ZHAO Li,CHEN Geng-hua,ZHANG Li-hua,et al.Applications of improved complementary pair adaptive noise cancellation to MCG analysis [J].Acta Physica Sinica,2004,53(12):4420- 4427.

[20] HYEJUNG K,SUNYOUNG K,VAN HELLEPUTTE N,et al.Motion artifact removal using cascade adaptive filtering for ambulatory ECG monitoring system [C]∥Biomedical Circuits and Systems Conference(BioCAS) IEEE.Hsinchu,Taiwan:[s.n.],2012:160- 163.

[21] ZHANG Huan-qian,ZHANG Shu-lin,DU Xiao-wei,et al.A multi-channel electrode-tissue impedance detection approach for motion artifact suppression in AECG [C]∥Computing in Cardiology.Nice:[s.n.],2015:117- 120.