基于像素相关的图像/视频压缩感知观测矩阵*
杨春玲 李林荪
(华南理工大学 电子与信息学院,广东 广州 510640)
压缩感知(CS)理论[1]是一个充分利用信号稀疏性或可压缩性的全新信号采集及编解码理论.它突破了传统采样中奈奎斯特定理对采样频率的限制,即要求采样频率应高于信号最高频率的两倍.压缩感知的核心思想是:对于一个稀疏信号或在某个正交基上稀疏的信号,通过低维观测值,利用重构算法求解非线性凸优化问题,也能使信号高概率地精确重构.压缩感知理论实现了在对信号采样的同时完成数据压缩的工作,为降低采集端的计算复杂度提供了强有力的理论支持,因此近年来压缩感知在图像/视频压缩成像、无线传感器网络等领域受到了广泛的关注[2- 5].
图像和视频信号的压缩感知包括了以下3个关键技术:①观测矩阵的设计;②信号的稀疏表示;③信号的重构.其中,观测矩阵在压缩感知及重构过程中起着十分重要的作用,观测矩阵的优劣直接影响信号的重构质量和重构算法的复杂度.Candès在文献[6]中提出了著名的关于压缩感知理论的有限等距性质(RIP),其中提到RIP性质是观测矩阵的一个充分非必要条件.在对图像/视频信号采集的过程中,由于自然图像中邻域像素具有一定的相关性,合适的观测矩阵可以在较低码率条件下获取较多信息量,从而得到较高的重构质量,因此观测矩阵的研究是图像和视频压缩感知的关键技术之一.
目前应用于压缩感知的观测矩阵分为两大类:①随机性观测矩阵;②确定性观测矩阵.随机性观测矩阵与确定正交变换矩阵(正交基)相关性不高,能够以极大概率满足RIP性质,是压缩感知理论和算法研究初期最常用的观测矩阵类型.其中高斯随机矩阵(GRM)和伯努利随机矩阵(BRM)是两种性能较好的随机性观测矩阵,结构化随机矩阵(SRM)是一种较新颖的随机性观测矩阵.高斯随机矩阵由满足独立同分布的高斯分布的元素构成,文献[7]中证明了高斯随机矩阵能与大多数正交基以较大概率满足RIP性质,是最常用的观测矩阵,但由于其复杂度高,占用内存多,不利于硬件实现.文献[8]中提出了随机伯努利观测矩阵,其每个元素都服从独立同分布的伯努利分布.由于其是由{1,-1}构成的矩阵,在观测和重构时减低了计算复杂度,使得重构速度很快,且在实际应用中易于实现.文献[9]中将一种新颖的结构化随机矩阵(SRM)[10]运用到视频压缩感知中,该矩阵的优点是具有良好的重构质量,计算复杂度低,且适用于大规模实时应用和分块处理的应用.总的来讲,使用随机性观测矩阵的重构质量良好,适用性广.但是由于随机性的存在,在实际应用中存在着信道传输和解码端接收上的缺陷.
确定性观测矩阵中的元素是用确定的方法构造出来的,具有结构确定的优点,易于存储,在实际应用中十分有利.对于经典的重构算法,性能较好的确定性观测矩阵包括托普利兹矩阵、基于混沌序列的矩阵、循环观测矩阵和二值化稀疏观测矩阵等.文献[11]中提出了在图像处理中确定形式的托普利兹矩阵及特殊形式的循环托普利兹矩阵.为了使观测矩阵在实际压缩感知应用上更加友好,同时为了保证更低的互相关性以保证不相关采样,文献[12]中提出了一种变形托普利兹矩阵,其优点在于只需要产生比高斯随机矩阵更小数量级的独立随机变量,即降低矩阵生成复杂度,减少矩阵的存储空间.缺点是对重构算法的适用性不是特别广泛,在一些重构算法上效果较差.基于混沌序列的矩阵是利用混沌序列构造出的观测矩阵.文献[13]中首先提出了一种基于混沌序列的矩阵,相比于其他观测矩阵构造技术,利用混沌系统产生的具有“伪随机”性质的观测矩阵与高斯随机矩阵类似地满足RIP准则.文献[14]中提出了一种基于混沌序列的循环压缩观测矩阵,该矩阵是利用Cat混沌映射构造混沌循环观测矩阵.其利用混沌序列的“伪随机”性质的同时,也利用到了循环矩阵存储空间小、硬件实现容易的特点,使得无论在性能上还是应用上相对于随机性观测矩阵都有很明显的优势.文献[15]中提出了一种基于B-J码的压缩感知确定性观测矩阵,文献中提出的第2类矩阵是一种确定性循环观测矩阵,其存储开销小,编解码复杂度也相对较低.确定性二值化稀疏观测矩阵是一种结构十分特殊的确定性观测矩阵,其元素仅由{1,0}构成.文献[16]中提出了一种基于LDPC码的二值化稀疏观测矩阵.由于其结构特殊,所以在实现上具有突出的优点,可以大大地减少观测矩阵的存储空间,并很大程度上减小重构复杂度,在实际应用中受到广泛关注.综上所述,确定性观测矩阵的结构稳定,十分适合硬件实现与实际应用.但是其适用范围较窄,一般某种确定性矩阵只适用于某种重构算法,而应用其他重构算法时,往往重构性能较差.
考虑到确定性观测矩阵在实际应用中的优势,以及稀疏观测矩阵在计算复杂度上的优点,基于图像相邻像素之间的相关性,文中提出一种应用于图像/视频信号压缩感知的观测矩阵,即基于邻近像素相关性观测矩阵(APM).首先设计一种合理的确定性二值化稀疏矩阵(矩阵中“1”值的位置对应的观测图像像素点称为目标点),然后利用高斯分布概率密度函数对水平和垂直两个方向上相邻像素点相应的观测矩阵元素分配权值,使得每个观测值中既包含目标点像素的信息,也包含目标点附近像素的少量信息,增加了观测值的信息量.这样构造出来的APM观测矩阵是确定性稀疏矩阵,具有存储量小和重构算法复杂度低的优点,由于每个观测值中只包含部分相邻像素的信息,重构时避免了较远像素信息的干扰,具有较高的重构质量.
1 图像/视频信号压缩感知的观测过程
设x∈Rn×1表示待测信号,利用观测矩阵Φ∈RM×N(其中M≪N)对观测过程进行描述:
y=Φx
(1)
yk=φk,1x1+φk,2x2+…+φk,N-1xN-1+φk,NxN
(2)
分块压缩感知(BCS)[17- 18]是图像和视频压缩感知中最常用的观测方法,整幅图像被分为若干个大小为B×B的小块,用观测矩阵分别进行观测.这种分块处理方式不仅仅具有节省观测矩阵的存储空间和加快重构速度的优点,还能在一定程度上提高图像的重构质量.一般地,分块大小B越大,重构质量越好;分块大小B越小,存储观测矩阵所需要的空间越小且重构速度也越快.在BCS中,观测过程表示为
yi=ΦBxi
(3)
式中:xi、yi分别表示第i块列向量化待测信号和对应的观测值;ΦB为大小为M×B2的观测矩阵,M=round(SR*B2),SR为采样率.
观测值传输到重构端,通过合理的重构算法恢复出原始图像或视频信号.观测矩阵在观测端和重构端起到很重要的作用,对压缩效率和重构性能有重要影响.
2 基于邻近像素相关性的观测矩阵
压缩感知中采集端观测过程是观测矩阵对信号的线性加权求和过程,当用高斯随机矩阵对信号进行观测时,得到的每个观测值都包含了信号的所有信息.而图像或视频帧内局部存在着一定的空间相关性,随机高斯矩阵观测矩阵没有考虑到这种空间相关性.为了利用图像或视频帧内的空间相关性,降低观测和重构时算法的复杂度,文中提出了基于邻近像素相关性观测矩阵(APM),使得对图像观测时,每个观测值只包含图像某个目标点及其邻近像素的信息,而不包含远离这个局部的像素信息.如此构造得到的观测矩阵是确定性稀疏矩阵,且在重构时,一方面能利用到邻近像素之间的空间相关性,另一方面排除了较远像素对当前像素的信息干扰,能得到更好的重构效果.
文中提出的邻近像素相关性观测矩阵(APM)的构造分两个步骤,首先根据采样率设计合理的二值化稀疏矩阵(矩阵中“1”值的位置在观测时对应的像素点称为目标点),然后利用高斯分布概率密度函数对水平和垂直两个方向上相邻像素点相应的观测矩阵元素分配权值,使得观测值中包含更多有用信息.
2.1 目标点的环形选择法及二值稀疏矩阵的生成
为了尽可能完整采集整个图像块的信息,目标点是根据采样率在整个图像块上均匀选择.根据采样率SR,利用以下3个步骤实现目标点的选择.
步骤1 划分环形区域
以图像块的中心2×2的区域为初始区域,如图1所示,每次向外1个像素形成一个方型的环形区域.若图像块大小为16×16,则有8个同心的环形区域(包括初始区域);若图像块大小为32×32,则有16个环形区域.
步骤2 计算每个环形区域内目标点数目
根据各个环形区域内像素点的总数和采样率,计算出各个区域内目标点的个数Mi:
Mi=round(SR*Ni)
(4)
式中,Ni为第i个环形区域内的总像素个数.
步骤3 目标点的环形选择法

图1 环形区域的划分Fig.1 Division of annular region
为了使目标点在图像块中均匀分布,将环形区域分为N、S、E、W4个方向区间,根据步骤(2)中确
定的目标点数以N→S→E→W的顺序循环、对称地取目标点.如图2所示,从N方向的第1个点开始选取,之后选取S方向的最后1个点、E方向的第1个点,最后选取W方向的最后1个点,以此循环.在1个方向内若有多个目标点则根据式(4)中计算出的目标点数和该环形区域内总像素点数等间隔取下个点.若在当前环形区域取点结束时没有完成一次完整的循环,则将循环延续到下1个环形区域,直到取满所有的目标点.

图2 环内循环取目标点方式Fig.2 Method of choosing target point in loops
目标点确定后,能很容易地生成一个维数为M×B2(其中,M为该采样率下的观测值个数)的二值稀疏矩阵P,其中每行只有一个元素为1,对应观测时图像块中相应的目标点.
2.2 基于邻近像素相关性观测矩阵的生成
由于自然图像相邻点之间具有一定的相关性,利用上述二值稀疏矩阵P作为观测矩阵观测图像得到的观测值恢复图像时能得到不错的重构质量.但由于相邻像素和目标点的像素值并非完全相同,由该二值稀疏矩阵得到的重构效果并非最优,因此,在二值稀疏观测矩阵的基础上,文中提出了APM观测矩阵,即考虑到相邻像素灰度值相近但不相同的特性,利用高斯分布概率密度函数对目标点的权值进行分散,一部分权值分散到相邻像素上,从而使得每个观测值中不仅包含目标点的信息,也包含邻近像素的少量信息,可进一步提高重构质量.
利用高斯分布概率密度函数,在水平和垂直两个方向上对2.1节得到的二值稀疏矩阵中的权值进行分散操作,把少量相关性较大的邻近像素点信息增加到观测值中:
(5)
式(5)表示APM观测矩阵中第k行的元素值分布.其中,(xtar,ytar)代表观测矩阵中该行元素对应的目标点坐标,(xi,yi)代表大小为B×B的图像块中所有的像素点的坐标,A、σx、σy分别为幅值和x、y方向上的方差,参数值的选取和采样率相关.
在不同采样率下,目标点的分布密度不同,高采样率下目标点分布的密度较大,选取较小的σ值,使得每个观测值只包含一个目标点及其少量相邻像素点信息,而不会过多地受到其他像素的影响;低采样率下目标点分布的密度较小,选取较大的σ值,使得每个目标点周围能有更多相邻像素被分散到权值.因此文中提出基于采样率的自适应参数选择策略,即让σx、σy与采样率成反比例地取值.
3 实验结果与分析
3.1 性能分析
为了验证文中提出的APM观测矩阵的有效性,对所提APM观测矩阵进行了仿真实验,和目前文献中较优的观测矩阵的仿真结果进行了对比.实验结果分为两个部分,一部分是对自然图像的观测和重构,另一部分是对视频序列的观测和重构.
第1部分对自然图像的压缩感知仿真中,分别利用分块BCS-SPL[17- 18]和OMP[19]算法重构图像.第2部分的视频压缩感知仿真中,利用文献[20]提出的两阶段多假设重构算法实现视频序列的重构.文中的仿真实验环境为搭载Inter Core i5 3.30 GHz处理器,内存4 GB的台式计算机;仿真实验均在64位Windows 7操作系统、Matlab R2014a上实现.
3.2 自然图像的实验结果
3.2.1 图像重构质量对比
实验图像为512×512的Lenna、Barbara、Peppers的pgm格式图像.文献[17]中提到在分块图像压缩感知处理过程中,分块大小会对重构质量产生很大的影响.当分块较小时,在存储上只需要较小的空间而且实现起来速度更快,但是重构质量相对较低;对应地,当分块较大时,虽然重构质量会相对较高,但是计算复杂度会相应地增大.因此通过实验折中选取分块大小为32×32.所有观测矩阵均在采样率为0.1、0.2、0.3、0.4、0.5的情况下进行实验.高斯随机矩阵、随机伯努利矩阵的结果为平均10次实验得到的,客观评价标准采用峰值信噪比PSNR.在图像实验中选取参数的经验取值公式为:A=0.95,σx=0.63-0.1SR,σy=0.55-0.1SR.
(1)基于OMP算法的重构效果对比
图3给出了利用文中提出的APM观测矩阵对图像分块观测,利用分块OMP重构算法的重构结果,同时给出了利用高斯随机矩阵[1- 2]、随机伯努利矩阵[8]和文献[14]中提出的观测矩阵对图像做相同分块观测的重构结果.其中GRM和BRM矩阵中的每个元素分别独立地服从高斯分布和伯努利分布.


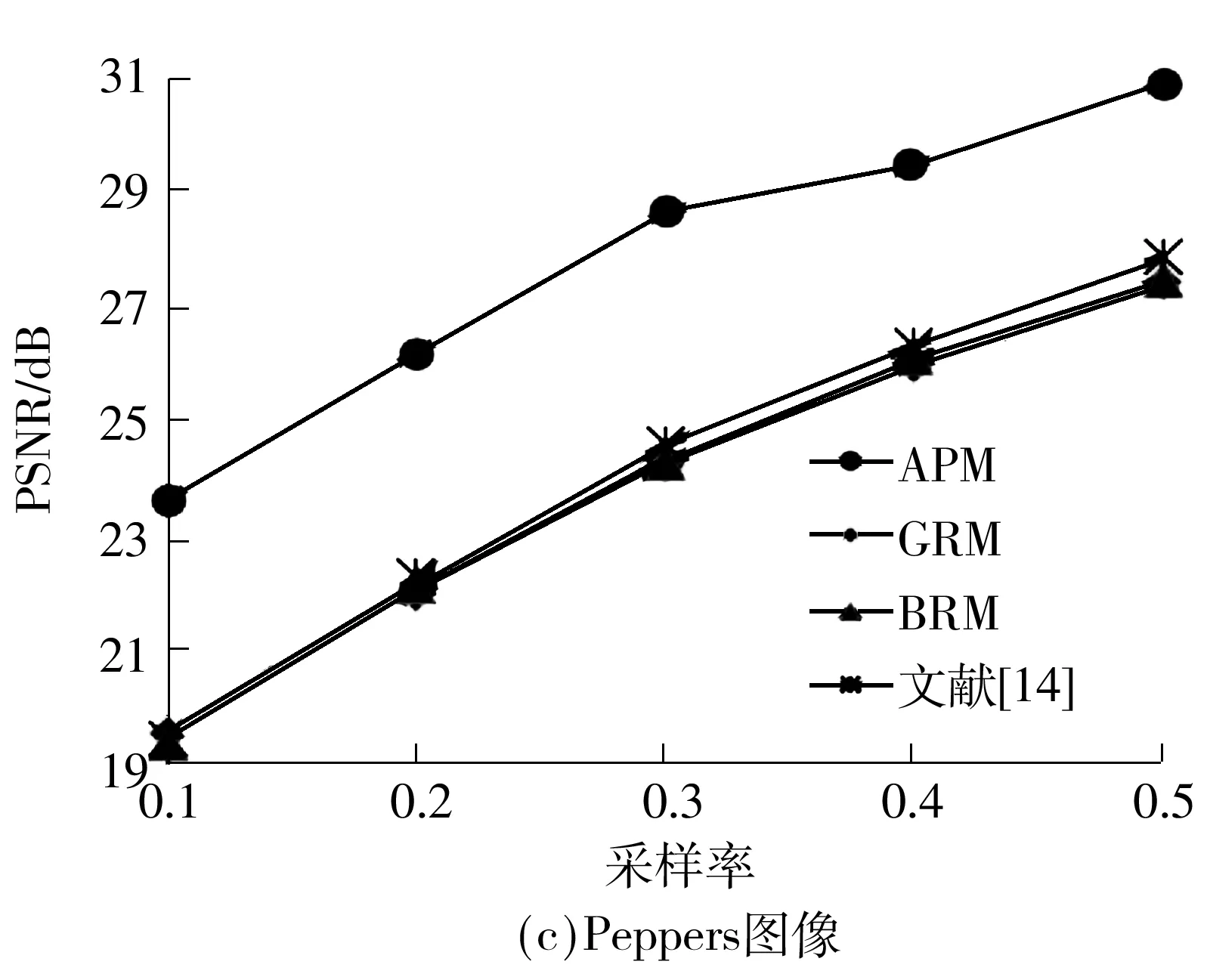
图3 不同矩阵在分块OMP算法上的重构质量对比
Fig.3 Comparison of reconstruction quality of different matrixes on BCS-OMP
图4给出了在采样率为0.3时,不同观测矩阵对Barbara的重构视觉效果.图2反映出利用文中提出的矩阵所重构出的图像客观性能有明显提升.在32×32分块、0.1~0.5采样率下,文中提出的观测矩阵对Lenna、Barbara和Peppers图像在分块OMP算法下重构的PSNR值较高斯随机矩阵、随机伯努利矩阵和文献[14]中的实验结果分别有平均3.47、3.43和2.97 dB的提升.由图4可见,文中提出的APM观测矩阵在视觉效果上有明显的提升,而其他矩阵块效应十分明显且细节重构效果一般.


图4 采样率为0.3时不同矩阵分块OMP算法Barbara视觉效果对比
Fig.4 Comparison of visual quality for Barbara using different matrixes on BCS-OMP when SR=0.3
(2)基于BCS-SPL的重构效果对比
图5给出了在不同采样率下,文中提出的APM观测矩阵利用BCS-SPL的重构性能结果,同时给出了高斯随机矩阵(GRM)、随机伯努利矩阵(BRM)和文献[15]中的观测矩阵的重构结果进行对比.图6给出了0.2采样率时对Pepper图像的重构效果图的对比.其中文献[15]的实验结果直接取自文献,其他观测矩阵的实验结果都是在和文献[15]相同的实验条件下仿真得到的,由于文献[15]中只给出了Peppers的仿真结果,因此文中也只对Peppers的重构性能和文献[15]的情况做了对比分析.由图5可见,文中所提APM观测矩阵具有最好的重构性能,对Peppers图像的重构PSNR值较高斯随机矩阵、随机伯努利矩阵分别有1.47、2.06 dB的提升,对比文献[15]中的实验结果也有0.69 dB的提升.从图6中可以观察到,即使在低采样率下,文中提出的APM观测矩阵的重构图像视觉效果相比于其他观测矩阵改善显著.在BCS-SPL算法下,利用文中提出的矩阵所重构出的图像已经十分清晰,而使用另外两个矩阵所重构出的图像,在图像局部有一定失真而且会感觉有些模糊.
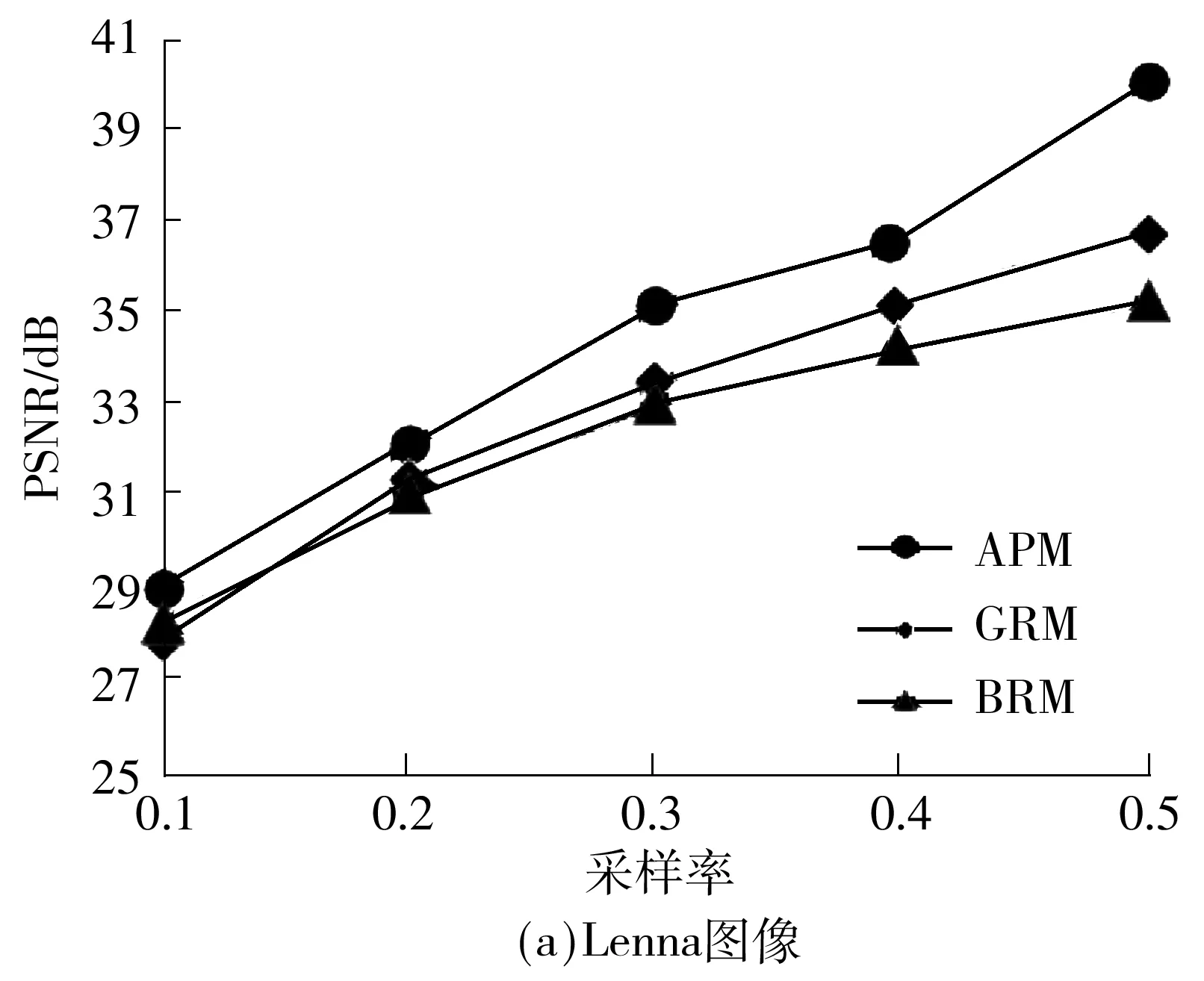


图5 不同矩阵在BCS-SPL算法上的重构质量对比
Fig.5 Comparison of reconstruction quality of different matrixes on BCS-SPL

图6 采样率为0.2时利用不同矩阵和BCS-SPL算法对Peppers重构的视觉效果对比
Fig.6 Comparison of visual quality for Peppers using different matrixes on BCS-SPL when SR=0.2
客观重构效果和主观视觉效果能提升的原因在于,APM观测矩阵的观测过程中尽可能地对原始信号中的像素点进行均匀采集,并增加邻近像素点的部分信息,得到的观测值中每个分量只包含一个目标点和其相邻像素的信息,而不包含远距离像素的信息,使得在重构时能利用图像邻近像素的相关性.由于其避免了较远像素信息的干扰,能充分挖掘自然图像的空间相关性,因而得到了较好的重构质量.
3.2.2 图像重构时间复杂度对比
由APM观测矩阵的生成过程可知,APM观测矩阵是确定性稀疏矩阵,利用BCS-SPL重构算法重构时,具有较小的计算复杂度,有利于实际应用.
表1给出了利用不同观测矩阵的具体重构时间.可见,文中所提的APM观测矩阵在BCS-SPL算法上的平均时间复杂度最低,尤其是低采样率情况下的时间复杂度下降最明显.由于文中矩阵在采样时对部分原始信号几乎进行了完整的采集,在重构的过程中减少了迭代次数,减少了向真实值逼近的时间;另一方面,每一个观测值只包含一个目标点和其邻域像素信息,而不包含远距离的像素信息,重构时受到较少不相关信息的干扰,能更快地逼近原始信号.
表1 不同观测矩阵和BCS-SPL算法对Lenna图像的重构时间
Table 1 Average reconstruction time for Lenna using different measurement matrixes and BCS-SPL

s
3.3 视频序列的实验结果
3.3.1 视频序列重构质量对比
该部分实验中,采用4组QCIF@15Hz的标准视频序列Coastguard、Football、Hall和Suzie的前2组GOP,这4组序列分别属于不同运动情况(快速、中速、慢速),以便更好地验证文中观测矩阵的适用范围.视频压缩感知重构过程使用文献[20]中所提出的两阶段多假设重构算法.在仿真实验中,文中对GOP=8和GOP=16两种情况进行分析(GOP=8,共17帧;GOP=16,共33帧).关键帧图像采样率Rkey选取为0.5,参数选择为A=0.95,σx=0.57,σy=0.55,非关键帧图像采样率Rn_key分别选取为0.1、0.2和0.3,其中非关键帧所使用的观测矩阵为关键帧的子集.

从表2可看出,文中提出的观测矩阵对视频序列有较好的重构质量及适用性,4个标准序列在GOP=8时相对于高斯随机矩阵有平均0.45、0.39、0.97和0.35 dB的提升,对于结构化随机矩阵分别有1.67、0.82、3.65和1.34 dB的提升.表3为4个标准序列在GOP=16时重构效果对比,相对于高斯随机矩阵分别有平均0.52、0.41、0.79和0.07 dB的提升,对于结构化随机矩阵分别有平均1.49、0.73、3.06和0.72 dB的提升.
表2 标准视频序列利用不同观测矩阵和2sMHR重构算法[20]时的重构质量对比(GOP=8)
Table 2 Comparison of reconstruction quality using different measurement matrixes and 2sMHR reconstruction algorithm[20](GOP=8)
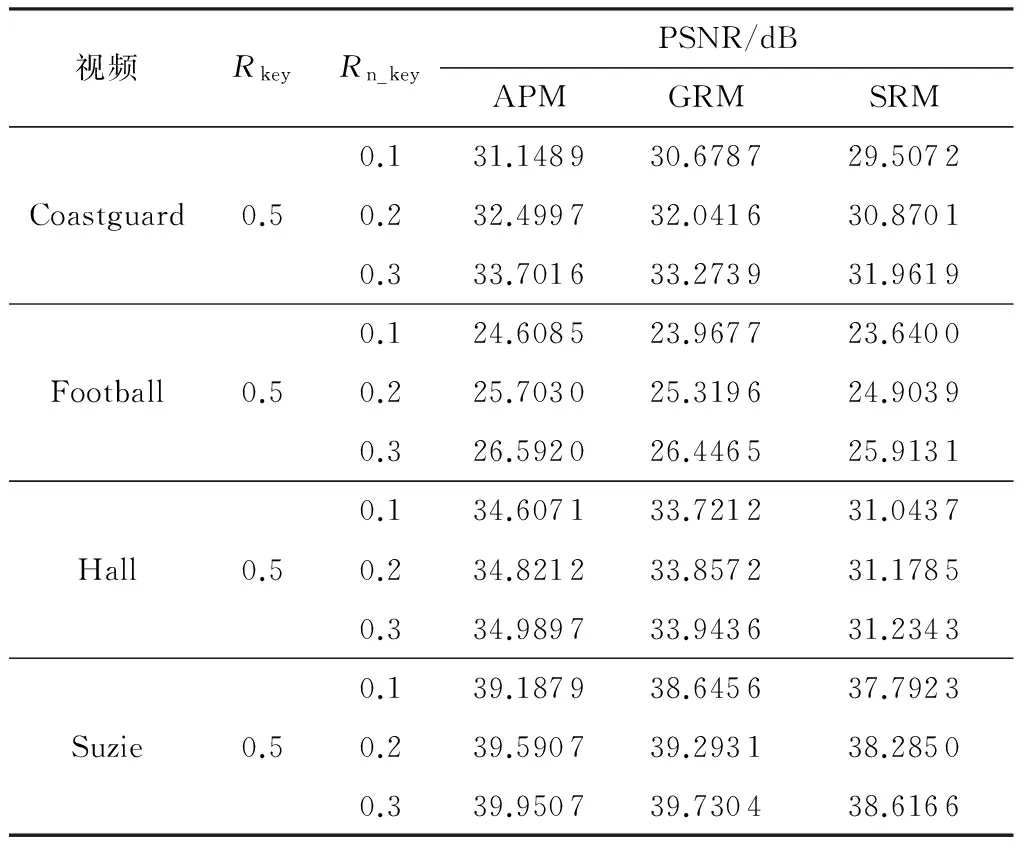
视频RkeyRn_keyPSNR/dBAPMGRMSRM0.131.148930.678729.5072Coastguard0.50.232.499732.041630.87010.333.701633.273931.96190.124.608523.967723.6400Football0.50.225.703025.319624.90390.326.592026.446525.91310.134.607133.721231.0437Hall0.50.234.821233.857231.17850.334.989733.943631.23430.139.187938.645637.7923Suzie0.50.239.590739.293138.28500.339.950739.730438.6166
表3 标准视频序列利用不同观测矩阵和2sMHR重构算法[20]时的重构质量对比(GOP=16)
Table 3 Comparison of reconstruction quality using different measurement matrixes and 2sMHR reconstruction algorithm[20](GOP=16)

视频RkeyRn_keyPSNR/dBAPMGRMSRM0.129.675729.236228.2165Coastguard0.50.231.581631.011730.08890.333.194432.648631.66280.123.429822.958622.7507Football0.50.225.306624.792024.45290.326.479726.213925.83310.132.908132.317530.1985Hall0.50.233.879333.056230.80050.334.406633.450031.00580.137.905437.684036.9789Suzie0.50.238.958038.959638.21070.339.534139.523639.0515
图7为标准视频序列Hall QCIF@15Hz在GOP=16、非关键帧采样率为0.1时第9帧的视觉效果.在高斯随机矩阵和结构随机矩阵重构效果图中,窗户和门等区域细节十分模糊,而邻近像素矩阵的重构效果细节就相对清晰.可见,在不同GOP下,在视觉效果和客观标准都有不同程度的提升,而且即使在低采样率下仍然具有较好的重构性能,具有一定的现实意义.


图7 Hall QCIF@15Hz第9帧视觉效果对比(GOP=16)
Fig.7 Comparison of visual quality of the 9th frame of Hall QCIF@15Hz(GOP=16)
3.3.2 视频序列重构时间复杂度对比
表4给出了GOP=16,利用不同观测矩阵观测,2sMHR重构时,平均每帧视频的重构时间.
表4 GOP=16时,Hall QCIF@15Hz 在文献[20]框架时的平均每帧重构时间
Table 4 Average reconstruction time per frame of Hall QCIF@15Hz using different measurement matrix and 2sMHR reconstruction algorithm[20]when GOP=16

s
由表4可知,3种不同的观测矩阵对于标准视频序列的时间复杂度的影响并不明显,文中提出的矩阵略降低了时间复杂度.这是由于对于视频压缩感知重构,匹配块搜索与预测是重构算法中最复杂的过程,因此观测矩阵对算法的影响很难体现.结合3.3.1节中的实验结果,在不牺牲时间复杂度的情况下,运用文中提出的邻近像素矩阵重构得到的序列仍有一定程度的质量提升.
4 结语
文中提出了一种基于图像/视频邻近像素相关性的观测矩阵(APM).利用APM观测矩阵得到的每个观测值只包含图像块中一个目标点和其邻域像素的信息,因此在重构时既可利用相邻像素的相关性,又避免了远距离像素信息的干扰,可得到较高的重构质量.另外,APM观测矩阵是一种确定性稀疏矩阵,具有观测和重构算法复杂度低的优点.实验结果表明,在不牺牲观测矩阵构造和重构过程复杂度的前提下,APM观测矩阵在客观标准和主观感受上都能有效提升图像和视频的重构质量,并且具有较广泛的适用性,在不同的采样率下利用分块OMP和BCS-SPL图像压缩感知重构算法、视频压缩感知的二阶段重构算法,都有良好的重构性能.
参考文献:
[1] DONOHO D L.Compressed sensing [J].IEEE Transactions on Information Theory,2006,52(4):1289- 1306.
[2] QAISAR S,BILAL R M,IQBAI W,et al.Compressive sensing:From theory to applications,a survey [J].Journal of Communications and Networks,2013,15(5):443- 456.
[3] 朱江,廖桂生,朱圣棋.基于块稀疏的空间碎片群目标成像方法 [J].电子与信息学报,2015,37(3):587- 593.
ZHU Jiang,LIAO Gui-sheng,ZHU Sheng-qi.Space group debris imaging based on block-sparse method [J].Journal of Electronics & Information Technology,2015,37(3):587- 593.
[4] 常侃,覃团发,唐振华.基于联合总变分最小化的视频压缩感知重建算法 [J].电子学报,2014,42(12):2415- 2421.
CHANG Kan,QIN Tuan-fa,TANG Zhen-hua.Reconstruction algorithm for compressed sensing of video based on joint total variation minimization [J].Acta Electronica Sinica,2014,42(12):2415- 2421.
[5] 武明虎,李然,陈瑞,等.利用视频非局部相似性的分布式压缩感知重构 [J].信号处理,2015,31(2):136- 144.
WU Ming-hu,LI Ran,CHEN Rui,et al.Distributed video compressive sensing reconstruction used nonlocal similarity [J].Journal of Signal Processing,2015,31(2):136- 144.
[6] CANDES E J,ROMBERG J,TAO T.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information [J].IEEE Transactions on Information Theory,2006,52(2):489- 509.
[7] CANDES E J,ROMBERG J K,TAO T.Stable signal recovery from incomplete and inaccurate measurements [J].Communications on Pure and Applied Mathematics,2006,59(8):1207- 1223.
[8] ZHANG G,JIAO S,XU X,et al.Compressed sensing and reconstruction with bernoulli matrices [C]∥Proceedings of IEEE International Conference on Information and Automation.Harbin:IEEE,2010:455- 460.
[9] LI R,LIU H,HE W,et al.Space-time quantization and motion-aligned reconstruction for block-based compressive video sensing [J].KSII Transactions on Internet and Information Systems,2016,10(1):321- 340.
[10] DO T T,GAN L,NGUYEN N H,et al.Fast and efficient compressive sensing using structurally random matrices [J].IEEE Transactions on Signal Processing,2012,60(1):139- 154.
[11] SEBERT F,ZOU Y M,YING L.Toeplitz block matrices in compressed sensing and their applications in imaging [C]∥Proceedings of IEEE International Conference on Information Technology and Applications in Biomedicine.Shenzhen:IEEE,2008:47- 50.
[12] ZENG L,ZHANG X,CHEN L,et al.Deterministic construction of toeplitzed structurally chaotic matrix for compressed sensing [J].Circuits,Systems,and Signal Processing,2015,34(3):797- 813.
[13] YU L,BARBOT J P,ZHENG G,et al.Compressive sensing with chaotic sequence [J].IEEE Signal Processing Letters,2010,17(8):731- 734.
[14] 郭静波,汪韧.基于混沌序列和RIPless理论的循环压缩测量矩阵的构造 [J].物理学报,2014,63(19):198402- 1.
GUO Jing-bo,WANG Ren.Construction of a circulant compressive measurement matrix based on chaotic sequence and RIPless theory [J].Acta Physica Sinica,2014,63(19):198402- 1.
[15] 夏树涛,刘璐,刘鑫吉.基于 Berlekamp-Justesen 码的压缩感知确定性测量矩阵的构造 [J].电子与信息学报,2015,37(4):763- 769.
XIA Shu-tao,LIU Lu,LIU Xin-ji.Deterministic constructions of compressed sensing matrices based on berlekamp-justesen codes [J].Journal of Electronics & Information Technology,2015,37(4):763- 769.
[16] LU W,KPALMA K,RONSIN J.Sparse binary matrices of LDPC codes for compressed sensing [C]∥Procee-dings of IEEE Data Compression Conference.Snowbird:IEEE,2012:405- 406.
[17] MUN S,FOWLER J E.Block compressed sensing of images using directional transforms [C]∥Proceedings of IEEE International conference on image processing.Cairo:IEEE,2009:3021- 3024.
[18] GAN L.Block compressed sensing of natural images [C]∥Proceedings of the 15th International Conference on Digital Signal Processing.Cardiff:IEEE,2007:403- 406.
[19] TROPP J A,GILBERT A C.Signal recovery from random measurements via orthogonal matching pursuit [J].IEEE Transactions on Information Theory,2007,53(12):4655- 4666.
[20] OU W F,YANG C L,LI W H,et al.A two-stage multi-hypothesis reconstruction scheme in compressed video sensing [C]∥Proceedings of IEEE International Conference on Image Processing.Phoenix:IEEE,2016:2494- 2498.

