尺规作图“倍立方”

☉江苏盐城市尚庄初级中学刘志才

☉江苏盐城市尚庄初级中学王寿云

尺规作图“倍立方”

☉江苏盐城市尚庄初级中学刘志才

☉江苏盐城市尚庄初级中学王寿云

一、倍立方问题

如图1，已知正方体ABCD-EFGH.

用尺规求作：正方体A′B′C′D′-E′F′G′H′，使得V正方体A′B′C′D′-E′F′G′H′=2V正方体ABCD-EFGH.

二、作图分析

图2

假定正方体A′B′C′D′-E′F′G′H′已经作出，如图2，设AB为1个单位长，则A′B′=个单位长.因此作出个单位长线段是解决问题的关键，这可借助平面直角坐标系来求解.

设正方体A′B′C′D′-E′F′G′H′的棱长为x个单位长，体积为y个单位长立方，则y=x3（x≥0）.我们知道，函数y= x3的图像为一支曲线，点（，2）（记为点M）在这条曲线上，我们可以通过列表、描点、连线等步骤画出函数图像，进而在图像上确定出点M（，2），从而得到表示个单位长的线段.事实上，画曲线时由于“连线”存在误差，会导致点M的位置不准确，根本的问题是这种方法不属于尺规作图的方法，用这种方法来求解显然是错误的.但作直线时“连线”不存在误差，如果点M在一条直线上，那么所求点M的位置就是准确的，且所求得的个单位长线段才是尺规作图所得.

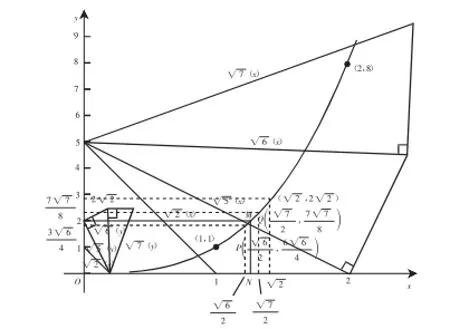
图3

通过上述方法处理后的曲线就显得较为扁平、平滑了，但仅这一点还不够，还需要在曲线上截取我们所需要的极小部分，以确保局部曲线直线化.方法是：找出左、右都逼近点M（，2）的点P和点Q.由于≈ 1.260，注意到是左、右逼近23■的较近的两个值.这样取值的目的，就是为了截取曲线中的极小部分，将PQ部分直线化，点M在PQ上，从而确保点M在直线PQ上.

通过以上两次处理后，确保了点M在直线PQ上，接下来就是要确定点M在坐标系中的准确位置，在x轴上确定出表示个单位长的线段，从而作出所求正方体.

三、作图实例

步骤1：作x轴垂直于y轴，垂足为O，在x轴上以已知正方体的棱长AB为x轴上的1个单位长，以个AB长作为y轴上的1个单位长作出平面直角坐标系，如图3.

说明：x轴上的单位长和y轴上的单位长不统一，这并不影响x轴上所有线段单位长的比值，也不会影响y轴上所有单位长的比值.随着n值的逐步增大，曲线就显得越来越扁平、平滑，就会有越来越多的点集中在同一条直线上.局部曲线直线化的范围也同时被扩大.

步骤3：在y轴上确定出表示2个单位长的点H，过点H作HM垂直于y轴，交直线PQ于点M.

步骤4：过点M作x轴的垂线交x轴于点N.

步骤5：以ON的长为所求正方体的棱长作出正方体A′B′C′D′-E′F′G′H′，则正方体A′B′C′D′-E′F′G′H′为所求，如图2.

说明：以上作图都是在尺规作图的范围内完成的，图3中的曲线连接部分不属于尺规作图的范围，只是直观地作为辅助说明曲线直线化的道理及证明求解的需要.另外，图1、图2均为将所作实际图形按一定比例缩小后的图形.

四、后语

用以上方法作一个正方体，可分别为已知正方体的3倍、4倍、…、n倍，关键是要恰到好处地找出左、右都分别逼进它们立方根的较近的两个值，以确保局部曲线直线化.

尺规作图的应用，是学生对所学知识点自我的综合考量与检测，是一次数学实验活动.学生必须要手脑并用，学会全面地、融汇贯通地进行分析与疏理，从中找出解决问题的方法.当然，我们还可以借助几何画板进行演练，使学生从中找到乐趣，这对于愉悦学生的身心有一定的好处，它迎合现代教育的主流方向，是培养学生创造力的有效途径.