一道课本习题背后的精彩

☉浙江绍兴市建功中学曹青

一道课本习题背后的精彩

☉浙江绍兴市建功中学曹青

《义务教育数学课程标准（2011年版）》在课程目标的总目标部分明确指出：通过义务教育阶段的数学学习，学生能体会数学知识之间的联系，运用数学的思维方式进行思考，增强发现问题、提出问题、分析问题、解决问题的能力.上述目标，无疑给教师的教学提出了更高的要求，可见教师教学时不仅要关注学生知识的学习过程，也要关注学生能力的培养.本文就以一道九年级下学期的课本习题的教学为例，通过变形、推广、延伸，展示教学的全过程，与同行交流.

一、原题呈现

九年级（下）“锐角三角函数”复习题中有这样一道习题：“证明：三角形的面积等于两边的长与其夹角的正弦值的乘积的一半.”

看到这道题，学生可以画出示意图，并将文字语言转换成如下的几何语言.

如图1，已知△ABC.

图1

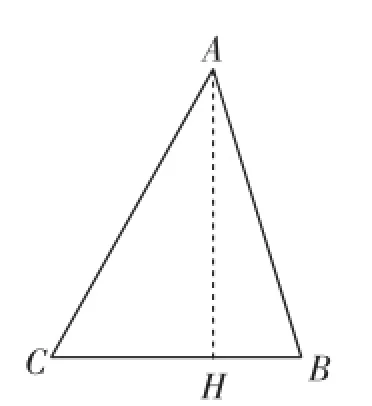
图2

证明：如图2，过点A作AH⊥BC，垂足为H.

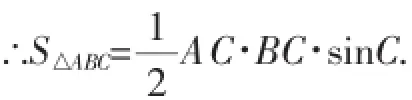
分析：本题是三角函数与思想方法的综合运用，是求三角形面积的一种重要方法，教材中以习题方式呈现，就

∴AH=AC·sin C.是给学生一种求三角形面积的新方法的探索机会.笔者认为本题在一章的最后复习题中出现，也是想让学生能从这个结论中经历探索其他四边形面积的求法的过程，而并非让学生就题论题，只要解决本题即可.教师在教学本题时，要注重引导学生注意文字语言向几何语言的转换过程，需强调几何语言的规范性，同时可以让学生用多种方法证明，注重学生发散性思维的培养.从考查内容上看，本题注重对基础知识、基本技能的考查，同时特别强调对基本活动经验、转化思想的考查；从考查方式上看，本题试图让学生经历多种解法的思考过程，可见一题多解、寻找解题的通性通法仍然为解题教学一个永恒的话题；从考查意义上看，本题注重知识间连贯性的考查，一以贯之地将三角形面积的研究向四边形面积的研究发展，是知识的拓展、运用的延伸，提醒教师授课时要重视知识发生、发展、探究的过程，把更多思考的空间和时间留给学生.

二、其他版本教材的探究

教材，是命题的发源地，也是命题的天然素材，可谓取之不尽、用之不竭，每年都有大量的中考试题直接源于教材，或以此为基础，改编、生成，焕然一新.所以，在中考复习前，用好教材这个重要的资源库，大有裨益，毕竟教材是经过专家多次打磨、精挑细选而成的作品，探其源、究其变、融其法一定是不可多得的捷径.笔者翻阅人教版教材，发现也有类似的问题.

人教版九年级（下）第85页第12题如下：

▱ABCD中，已知AB、BC及其夹角∠B（∠B是锐角），能求出▱ABCD的面积S吗？如果能，用AB、BC及其夹角∠B表示S.

图3

解：看到这道题，学生可以画出示意图（如图3）加以解决.连接AC，可以把▱ABCD分成两个全等的三角形，根据“三角形的面积等于两边的长与其夹角的正弦值的乘积的一半”，可知=AB·BC·sin B，所以S=▱ABCDAB·BC·sin B.

分析：本题是苏科版教材习题的变形，难度略有上升.事实上，三角形是我们研究几何图形的基础，当三角形研究过后我们经常会将其结论推广到四边形中，比如，全等三角形研究完后我们会研究全等四边形，这是一种经验的迁移，也是学生必须具备的研究数学的一种方式.平行四边形又是四边形中非常特殊的一种图形，可以看作是由两个全等的三角形所组成的，所以利用三角形的相关结论，很容易得到平行四边形面积的求法.

三、一般化探究

研究完平行四边形的面积，将条件再一般化，任意四边形的面积的求法是否也可以用类似的方法研究呢？

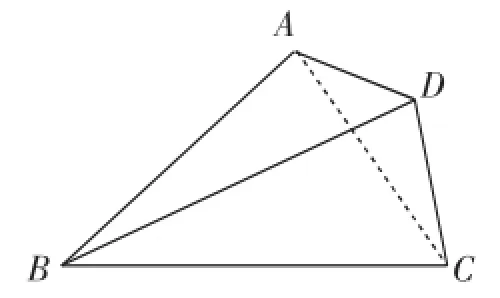
图4

解：连接AC，可以把四边形ABCD分成两个三角形，根据“三角形的面积等于两边的长与其夹角的正弦值的乘积的一半”，可知S△ABC=AB·BC·sin B=AD·DC·sin D，所以S=四边形ABCDAB·BC·sin B+AD·DC·sin D.

分析：本题是人教版教材习题的变形，将条件一般化进行研究.事实上，此题的提出是学生十分容易想到的，因为特殊四边形研究过后，必然会对一般四边形进行研究，这也是我们研究数学的一种常用做法.从解题教学的角度看，此问题“源”于学生对题目条件之间联系性的理解，体现了知识间的连续性.

纵观以上问题，都“源”于课堂上经验、方法的积累.事实上，“三角形的面积等于两边的长与其夹角的正弦值的乘积的一半”这一结论对于学生来说并不陌生，课堂上教师也会研究，但是鉴于课堂进度、教师未考虑学生思维的发展性等诸多原因，教师在教学时往往给予学生探索的时间和空间远远不够，使学生对这一结论的认识和运用都偏浅，缺少该有的过程体验，也未能获得该有的深层次结论.所以教学时，这一习题一定要用好，使其背后蕴含的知识间的联系让学生深刻体会到.

四、推广探究

上述研究仅限于对三角形、四边形的边、角与面积之间的探索，仅仅体现了一法多用.而数学的教学又讲究一题多解，所以对于四边形我们还可以从对角线、对角线的夹角进行深入研究.

如图5，设四边形ABCD的两条对角线AC、BD所形成的锐角为α，分别过点A、C作AH⊥BD，CG⊥BD，垂足分别为H、G.

图5

∵在Rt△AHO与Rt△CGO中，AH=OA·sinα，CG=OC·sinα，

分析：此法将四边形分割成两个三角形进行研究，从而求出四边形的面积与对角线的长及对角线的夹角之间的关系.此法源于学生对菱形面积求法的理解，八年级在学习菱形时，学生知道菱形的面积等于对角线乘积的一半，继而得到结论“只要一个四边形的对角线互相垂直，则它的面积总是等于对角线乘积的一半”，当时所用到的方法就是将其面积拆分成两个三角形的面积进行研究.

其实，此结论完全可以直接转换成三角形的面积加以解决.

如图6，过点C作BD的平行线，在平行线上取CM=BD.

过点A作AN⊥CM，垂足为N.

易得S四边形ABCD=S△ACM.

∵CM∥BD，

∴∠ACM=∠AOB=α.

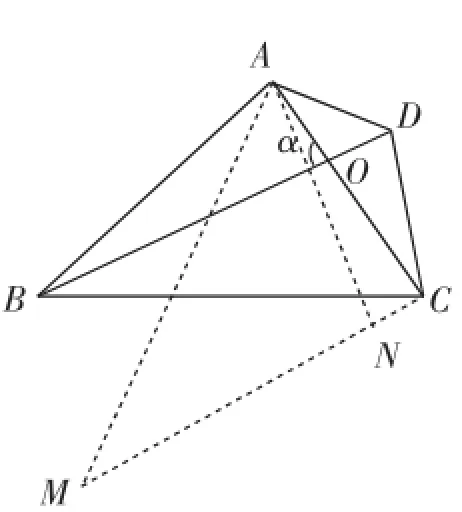
图6

由“三角形的面积等于两边的长与其夹角的正弦值的乘积的一半”，可得S=MC·AC·sin∠ACM=MC·△ACMAC·sinα.

分析：此法巧妙地将四边形的面积转换成三角形的面积，继而转换成“题源”，将四边形与三角形紧密相连，相当巧妙.此法源于学生对三角形面积的求法的理解及对四边形与三角形关系的理解，在学生的理解中，看到四边形很容易联想到三角形，从而进行转换.当然，此解法还可以转换成平行四边形加以解决，如过点A、C作BD的平行线，过点B、D作AC的平行线，交点分别为E、F、G、H，则四边形EFGH是平行四边形，又知四边形ABCD的面积是四边形EFGH面积的一半，根据“人教版教材习题”可得结论.

将四边形面积与边、角的关系推广到四边形面积与对角线、对角线所成的锐角的关系并不是偶然，因为四边形的对角线是研究四边形时重要的一个研究要素，很容易产生不同的作法、新的认识，这就是学生在课堂上实现创造的体现.

弗莱登塔尔曾说：学习数学唯一正确的方法是实现“再创造”.故在课堂上模仿是需要的，如从三角形的边、角、面积的研究到四边形边、角、面积的研究，但模仿只能让学生“学会”，并未“会学”，所以教师要关注学生在课堂上知识的创新、整合，如从四边形边、角、面积的研究到四边形对角线、夹角、面积的研究，让学生经历已有的体验到未有的经验过渡的过程，得到更多的收获.

五、反思探究

上述研究结束后，可以让学生回到最初的地方再次体会、感悟，比如，三角形的面积等于两边的长与其夹角的正弦值的乘积的一半，即AC·BC·sin C，若∠C=90°，会怎么样？这样学生可以体会到当∠C=90°时，=AC·BC，所以sin90°=1.让学生感受到原来锐角之外也有三角函数，为日后的数学学习埋下伏笔.同时还能研究钝角的问题，让学生感受钝角三角函数的存在，这样会加深学生对三角函数、三角形面积的求法的理解.

六、感悟思考

1.重结果更重过程.

中考的作用本是初中教学的指挥棒和方向标，对平时的教与学起着指导性的作用.但随着学校多方因素的干扰，“功利性”愈演愈烈，只求结果、注重高分，让素质教育流于形式，凡是中考考点一定进行大量的机械训练，认为数学教学等同于解题教学、题型教学，更甚者认为是一种刺激—反应—模仿的学习过程.这样的模式严重遏制了学生能力的后续发展，所以日常的教学中一定要关注知识发生、发展的过程，课堂上，多给学生思考的时间和空间，树立起正确的教学观念，认识到学生获得知识必须建立在自己思考的基础上.文中三角形面积的探索恰好是很好的一例，在素质教育的课堂上要多多出现，同时，课堂上要多鼓励学生自主探究问题，经历发现问题、提出问题、分析问题、解决问题的过程，让学生的发散性思维得到培养.

2.重知识更重能力.

无论什么性质的考试，都非常注重对“四基”的考查.所以教师的课堂教学，应注重学生对基础知识、基本技能的理解和掌握，感悟数学思想，积累数学活动经验.故在教学活动中，教师应首先夯实学生的基础，确保深刻理解，同时鼓励与提倡多样化教学，不仅要求目标、手段多样化，更要注重解决问题策略的多样化，激发学生的好奇心和求知欲，通过学生自主的思考、尝试等过程，创造性地解决问题，从而提高数学的能力.本题的出发点就是从一个简单的三角形公式出发，重视基础知识、基本技能，教师教学时开展研究性学习，让学生获得该有的数学经验.

3.反思，不忘初心.

波斯纳说：经验+反思=成功.所以无论是教师的教还是学生的学都要有反思的过程.事实上，数学知识的教学，一定要多关注知识的“生长点”和“延伸点”，把每节课上成一节生长延伸数学课，从一个小问题出发，让学生的数学思维自由生长，延伸出各式各样的好问题，把每一堂课的知识整合成一个体系，注重知识的结构与体系之间的联系，处理好局部知识与整体知识的关系，最终无论问题延伸到何方，都要回过头再去看那颗“初心”，这样会有更高层次的理解，可谓“会当凌绝顶，一览众山小”.本题的教学自成一个体系，从三角形出发，研究到四边形，再推广到多种方法，最后回到三角形，看到别人不曾看到的知识.

一道课本习题，有简单的结论，有简单的方法，又有不简单的思考，不简单的精彩，中考复习时，一定要为学生数学的长远发展考虑，这才是每位教师该做的.