基于最优化模型的太阳影子定位方法*

陈晓雪，汪劲希，王天钰（电子科技大学，成都 610054）

基于最优化模型的太阳影子定位方法*

陈晓雪，汪劲希，王天钰
（电子科技大学，成都 610054）

针对利用太阳影子实现目标的定位问题，分析得到影响影子长度的参数，确立了影长与太阳高度角、目标物长度、经纬度等的函数关系，并结合最小二乘法思想，建立了以理论影长与实际影长之差的平方和最小为目标的优化模型。以直杆为例，运用粒子群优化算法快速求解得到目标的可能位置，并与实际地点进行了比较。

太阳影子定位，最小二乘拟合，粒子群优化算法

0 引言

目前，导航定位技术已然贯穿于我们生活的方方面面，在信息化战争中，对目标打击物实现快速定位的重要性也毋庸置疑。随着科技的不断进步，定位的方法日新月异，不断发展，如GPS定位、基站定位、WIFI定位、RFID/二维码等标签识别定位、声波定位、场景识别定位等等，对于不同的环境，每种定位技术都有其不同的使用效果，可根据实际应用采取一种或多种混合技术。在探测条件比较恶劣或工具匮乏的野外环境下，GPS等一些定位方法由于设备条件的限制而无法达到理想的效果，本文提出一种利用太阳影子对目标物进行定位的方法，利用该技术确定地点的关键是通过分析影响影子长度的参数，确定目标所处地点的经纬度与影子长度的关系。通过测量收集一段时间内影子顶点坐标数据建立最优化模型，并利用收敛速度较快的粒子群优化算法在全局范围内进行求解，从而对目标物所处地点作出预测。

1 太阳影子理论长度的计算

在太阳光的照射下，不透明的物体在与光照方向相反的朝向下出现影子。以直杆为目标物，当其固定在水平地面上，影子的长度受直杆长度与太阳高度角的影响，在直杆长度一定的情况下，太阳高度角越小，直杆影子越长，分析其几何关系可以得到直杆太阳影子的长度满足

其中，L为固定直杆的长度，l为固定直杆太阳影子的长度，α为太阳高度角。

1.1 太阳高度角α的确定

太阳高度角α是太阳光的入射方向和地平面之间的夹角，在日出和日落时达到最小，正午时太阳高度角最大，物体的影子长度最短。以地球球心为原点，赤道平面内指向太阳直射经线的方向为x轴，地球自转轴方向为z轴，建立右手空间直角坐标系［2］，如图1所示。

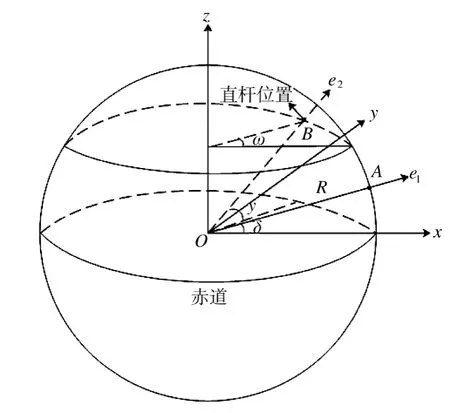
图1 以地球球心为原点建立空间直角坐标系

图1中，e1为太阳直射方向的单位向量，e2为固定直杆方向的单位向量，δ为当天的太阳赤纬，即太阳直射纬度，y为直杆的纬度，ω为太阳的时角，R为地球半径通过分析几何关系，可得向量OA和OB 为

根据式（2）可得向量OA和OB的夹角余弦，即

直杆所处地点某一时刻的太阳高度角满足

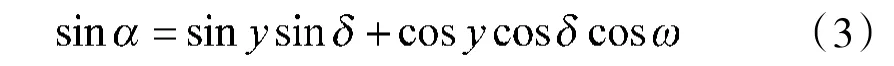
1.1.1 太阳赤纬δ

太阳赤纬是地球赤道平面与太阳和地球中心的连线之间的夹角，在每年夏至时达到最大值+23 °26'，冬至时达到最小值-23°26'，春分和秋分时太阳直射赤道，此时太阳赤纬为0，由此其以年为周期，成为季节的标志。设n为日期序号，每年的1月1日为n=1，2月1日为n=32，以此类推，则一年中任何一天的太阳赤纬［1］为

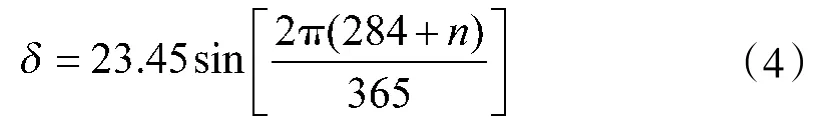
1.1.2 时角ω

时角表明一天中时间的变化，在同一时刻，对同一经度，太阳对应的时角相同，地球自转360°对应一天的24 h，故每小时对应的时角为15°。以正午12点为0°算起，上午时角为负值，下午时角为正值，其计算式［1］为

式中，t为当地时间，采用24 h制。

位于不同地点的直杆处于不同的时区，为了得到其在不同地点对应的时角，以北京时间t0为标准时间，结合所处地点的经度β进行换算，计算得到时角的表达式为

因此，将式（4）、式（6）代入式（3），结合式（1），得到太阳影子理论长度为

分析可知，日出到正午12点期间，太阳对应的时角为负值，日出时太阳高度角为0°，影子长度最长，随着时间推移时角逐渐增大，太阳高度角逐渐增大，当到达当地正午12点时时角为0°，太阳高度角达到最大值，此时影子长度为一天中最短；正午12点到日落期间，太阳对应的时角为正值，随着时间推移时角逐渐增大，太阳高度角逐渐减小，日落时太阳高度角为0°，影子长度再次达到最长。

利用余弦函数的对称性，当上午和下午的时刻与正午12点的时间间隔相等时，两个时角互为相反数，余弦值相等，故两个时刻下对应的太阳高度角相同，对于同一根直杆来说，两个时刻的太阳影子长度相等。因此，一天中太阳影子长度以正午影长为中心向日出和日落影子呈对称增长，以12点为对称轴的时刻下影子长度相等，在日出和日落时达到最长，且影子长度相等，在正午时太阳影子长度达到最短。

2 太阳影子顶点坐标确定直杆所处地点的优化模型

为了利用直杆的太阳影子变化确定直杆所处的地点，利用直杆的经纬度与直杆长度表示出直杆太阳影子的理论长度，与可测得的直杆实际影长进行比较，从而确定使理论值与实际值最接近的直杆地点与直杆长度。

2.1 模型的建立

2.1.1 目标函数的确定

以直杆底端为原点，水平地面为xy平面建立坐标系，根据固定直杆不同时刻在水平地面上的太阳影子顶点坐标（xi，yi），可以得到每一时刻下直杆的实际影子长度li实际。

由于一天中太阳影子长度以正午影长为中心向日出和日落影子呈对称增长，关于12点对称的时刻下影子长度相等，在正午时太阳影子长度达到最短，利用这一规律，在得到不同时刻下直杆的实际影子长度之后，将实际影子长度拟合成关于北京时间t0的二次曲线，找到实际影子长度取最小值时对应的时刻tn，tn即为对应的北京时间，与当地时间的正午12点相对应，设x为固定直杆地点的经度，经换算可得直杆所处地点的经度为

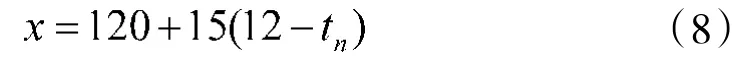
假设i时刻下直杆所处地点的太阳高度角为αi，影子长度为li，结合式（3），可解得i时刻下直杆所处地点的太阳高度角αi，则直杆的太阳影子理论长度li理论为

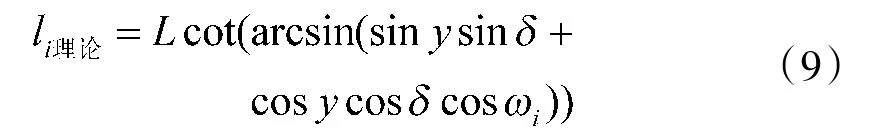
式中，ωi为i时刻下的时角，设t0i为i时刻下的北京时间，根据时角的表达式（6），有

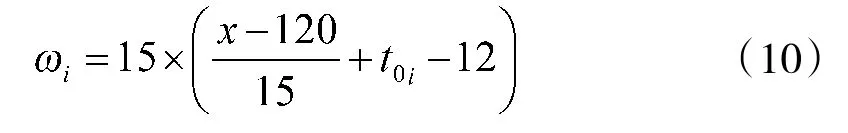
当每一时刻直杆太阳影子的理论长度与实际长度足够接近时，即目标函数F达到最小值，可以根据对应的直杆长度与直杆地点经纬度取值确定直杆所处的地点。结合式（9）、式（10），利用最小二乘法的思想，本文建立以直杆长度与直杆纬度为决策变量的优化模型的目标函数F

式中，k为太阳影子顶点坐标的个数。

2.1.2 约束条件的确定

考虑直杆长度与直杆经纬度的实际约束因素，将地球按纬度区分，分为北纬和南纬，以北纬为正，南纬为负，故列得以下约束条件。

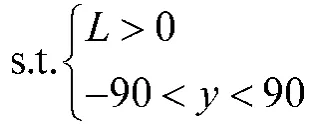
综上，得到太阳影子顶点坐标确定直杆所处地点的优化模型

约束条件:

2.2 模型的求解

以2015年4月18日在18.3°N，109.5°E处测得的太阳照射下某直杆的影子顶点坐标数据（如表1所示）代入模型进行求解。

表1 太阳影子顶点坐标数据

2.2.1 确定太阳赤纬δ

直杆太阳影子的顶点坐标数据测量于2015年4月18日，从2015年的1月1日起计数，到4月18日共108天，将n=108代入式（4），得到当天的太阳赤纬δ为

2.2.2 确定直杆所处地点的经度x

将表1中北京时间14∶42-15∶42期间的太阳影子顶点坐标代入影子实际长度表达式（8），利用Matlab将直杆的实际影子长度拟合出关于时间t的二次曲线，求解得到当tn1=12.65 h，即北京时间12∶39时直杆影子长度达到最小值，此时为当地时间12∶00。

将tn1=12.65 h代入式（9），求解得到直杆所处地点的经度x1为

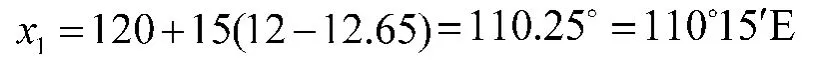
2.2.3 确定直杆长度与直杆所处地点的纬度

将表1中某固定直杆在水平地面上的21组太阳影子顶点坐标数据、太阳赤纬δ=10.51°，tn1=12.65 h，k=21代入优化模型，利用粒子群优化算法［3］进行求解。

算法原理:

粒子群优化算法属于进化算法的一种，其基本思想是:初始化一群拥有位置与速度属性的随机粒子，通过多次迭代，在粒子空间中寻找到最优解。其中，位置属性指的是在某次迭代过程中各个决策变量的值，速度属性决定了每次迭代过程中粒子位置属性改变的方向与大小。在每次迭代过程中，粒子会以靠近个体极值与全局极值为目的来调整自身的位置与速度，个体极值是指单个粒子到目前为止发现的最好位置，即自身找到的最优解，全局极值是指整个粒子群体经历的最好位置，即粒子群目前找到的最优解。

随机建立一个含有m个粒子的粒子群以及一个d维空间，第i个粒子在空间中的位置与速度分别用集合Xi={xi，1，xi，2…xi，d}、Vi={vi，1，vi，2…vi，d}记录。在迭代过程中找到的个体极值PB与全局极值GB分别用集合Pi={pi，1，pi，2…pi，d}、Pg={gi，1，gi，2…gi，d}记录。个体极值与全局极值每更新一次，粒子群中每个粒子便按照以下规则更新自己的位置与速度属性:

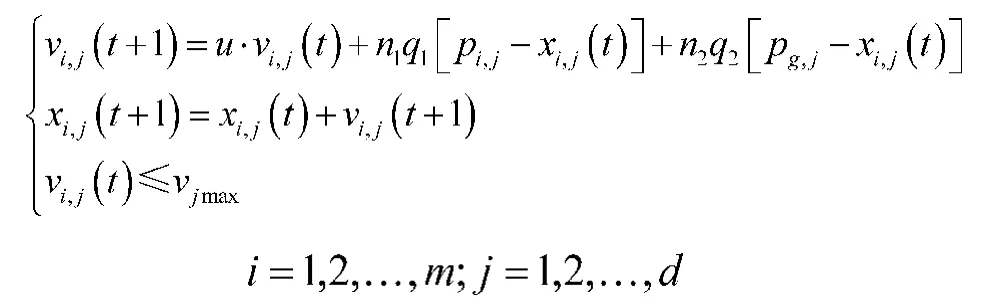
式中，u代表惯性因子，表示粒子对当前速度继承的比例，u＞=0；n1与n2为学习因子，即粒子向群体内或邻域内最优点靠近的能力，n1，n2＞=0；q1，q2为随机数且q1，q2∈［0，1］；t代表第t次迭代过程；vjmax指的是粒子第j个位置参量的最大速度，其值决定相应的决策变量在一次迭代中改变的最大值；u，n1，n2皆为常数值。

粒子群优化算法的性能受控制参数取值的影响很大，应该遵循以下原则对各参数进行赋值:

粒子数:对于一般优化问题，通常取m∈［20，40］；对于复杂优化问题或者是特定优化问题，取m≥100。

学习因子:取n1=n2且n1，n2∈［0，4］。

惯性因子:对于基本粒子群算法，取不大于1的常数即可。

空间维度:取优化问题中决策变量的个数。

粒子的最大速度:通常设定为相应决策变量的取值范围宽度。

粒子群优化算法步骤如以下框图所示:

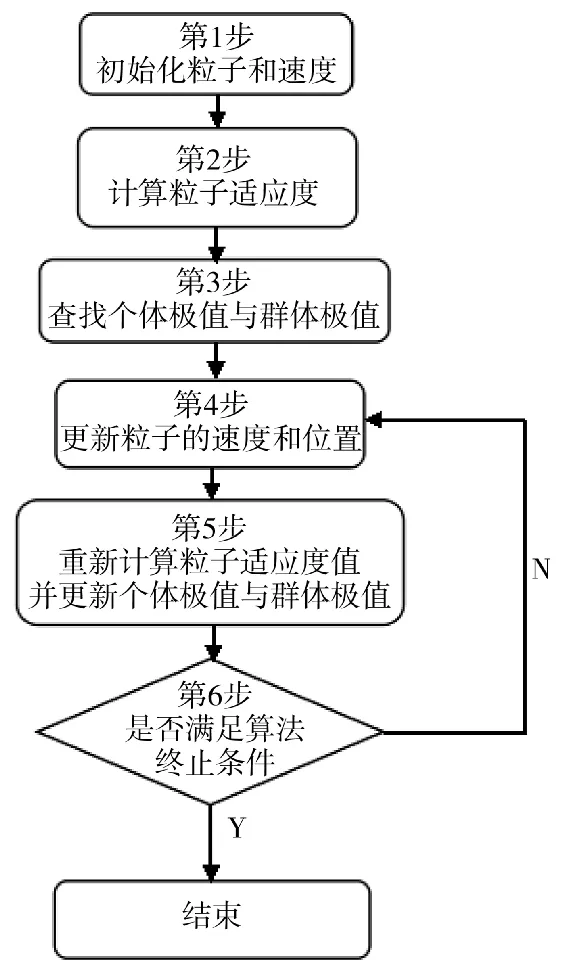
图2 粒子群优化算法框图

考虑直杆地点的经度由拟合直杆的影子长度得到，因此，在求解直杆长度与直杆纬度时在求得直杆经度的基础上增加正负2°的随机扰动，取粒子数m=50，学习因子n1=n2=1.5，惯性因子u=0.5，利用粒子群优化算法求解，得到当目标函数取得最小值时直杆长度与直杆纬度的取值如表2所示。

表2 直杆长度与直杆所处地点纬度的最优解

由表1可知，当直杆的长度在2.50 m左右，直杆纬度取20°左右时，目标函数F可取得最小值，结合之前计算得到的直杆经度110.25°，得到表1中直杆的可能地点如表3所示。

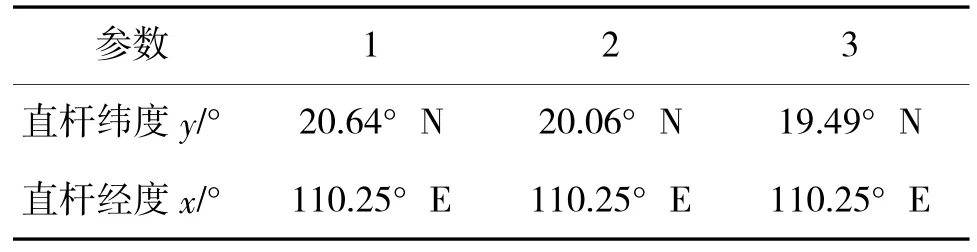
表3 直杆的可能地点列表

通过求解模型得到直杆所处的可能位置，以19.49°N，110.25°E为例，利用三面角余弦定理，可得该结果与直杆实际所处地点（18.3°N，109.5°E）地理距离相差约154.06 km，说明这一模型对目标物直杆实现了粗略定位。对模型结果进行误差分析，确定直杆影子顶点坐标时引入测量误差影响了实际影长的准确性；同时地球是一个椭球体，在建立模型时将其视作球体并忽略地球表面地形带来的误差也会影响精度。模型的不足之处在于定位精度不高，但是应用该模型对目标实现定位时对测量设备要求低，且求解速度快，可在利用该模型实现粗略定位的基础上，进一步结合其余定位方法对目标物进行精确定位。

3 模型的推广

在无法获得太阳影子顶点坐标的情况下，可通过拍摄视频的方法获取有效信息，太阳影子的长度与朝向随时间的推移逐渐发生变化，可利用Matlab对视频中的画面进行灰度处理和二值化，提取出目标影长的像素点，再通过抓取影子长度的像素点坐标计算得到任一帧画面中的实际影子长度，以直杆位置为变量表示出太阳影子的理论长度，仍以太阳影子长度的实际值与理论值之差作为目标函数，寻找使太阳影长的实际值与理论值最接近的视频可能拍摄地点。目前在无人机的航拍侦察中，存在随飞行距离增加而精度下降、对地形复杂地区定位误差大等问题，利用该模型对目标物所处环境要求低的特点可先找到目标的粗略位置，缩小定位范围之后再进行侦查、监视、遥感等，如需进行电子对抗、测绘等可再进一步结合其他技术增加定位精度。

4 结论

本文以直杆为目标物为例，通过分析影响直杆太阳影子长度的因素，得到以直杆所处地点的经纬度与直杆长度为参数的太阳影子理论长度函数关系式，结合可测得的直杆实际影长，利用最小二乘思想，建立了以直杆经纬度与长度为决策变量的优化模型，并利用粒子群优化算法对优化模型进行求解，提高了模型的效率，为利用太阳影子实现定位提供了一种简捷的科学方法。该定位方法对设备依赖性小，成本低，可广泛应用于对定位精度要求不高的场所。除此之外，将该方法与其他一些高精度的目标定位方法联合使用，如结合多源影像的匹配技术应用于军事目标侦察或地面位置勘测，可进一步扩大其适用范围，具有一定的现实意义与参考价值。考虑地球自转速度的变化以及日地相对位置变化带来的影响，引入修正参数对相关参量进行修正，进一步提高模型的精准度。

［1］方荣生.太阳能应用技术［M］.北京:中国农业机械出版社，1985.

［2］肖志勇，刘宇翔.一种新的纬度测量方法［J］.大学物理，2010，29（9）:51-54.

［3］张建林.MATLAB&Excel定量预测与决策——运作案例精编［M］.北京:电子工业出版社，2012.

Sun Shadow Positioning Method Based on Optimization Model

CHEN Xiao-xue，WANG Jin-xi，WANG Tian-yu
（University of Electronic Science and Technology of China，Chengdu 610054，China）

To achieve the object localization by the sun shadow，the paper analyzes the parameters which influences the length of the shadow，and establishes the function of the shadow length and the solar elevation angle，the length of the target，the latitude and longitude，etc.Combined with the leastsquare method，the optimization model is built with the minimum square sum of the difference between the theoretical shadow length and the actual shadow length as the target.Take a straight rod for example，the possible target position has been quickly solved by use the method of the particle swarm optimization algorithm，which is also compared with the physical location.

sun shadow positioning，least-square fitting，particle swarm optimization algorithm

TN971

A

1002-0640（2017）03-0112-05

2016-02-06

2016-03-15

国家自然科学基金资助项目（11271001）

陈晓雪（1994- ），女，山西人，硕士研究生。研究方向：光通信与光电工程。