有限脊波变换环绕现象改进算法及其在版权保护中的应用
祝瑞玲 韩卓然
1(山东传媒职业学院信息工程系 山东 济南 250200)2(上海交通大学电子信息与电气工程学院 上海 200240)
有限脊波变换环绕现象改进算法及其在版权保护中的应用
祝瑞玲1韩卓然2
1(山东传媒职业学院信息工程系 山东 济南 250200)2(上海交通大学电子信息与电气工程学院 上海 200240)
Finite Ridgelet Transform(FRIT)能高效表示线的奇异特征,在多种领域广泛应用。但是由于它的“环绕”现象,影响了在图像处理中的应用。揭示了“环绕”现象和Finite Radon Transform(FRAT)域系数的关系,根据像素的空间相关性,以及对FRAT系数进行软门限阈值处理,提出一种改进算法,能够去除“环绕”现象。依据最大后验概率(MAP)准则选择大能量的改进有限脊波变换(Modified Finite Ridgelet Transform-MFRIT)系数,版权信息嵌入其中。实验结果表明,该算法具有更好的鲁棒性和透明性。
有限脊波变换 版权保护 环绕 MAP
0 引 言
在目前的互联网时代,存储和传输技术飞速发展,图像(视频)编辑工具非常容易获得与应用,数字产品的修改越来越广泛,因此它们的版权保护尤为重要。采用数字水印技术保护版权所有者的合法权益,是一种简便有效的方法。数字水印版权保护,就是采用某种方式在数字产品中嵌入代表版权的信息,以保护数字产品的版权。这种方法几乎不占用额外的存储空间,同时还可以实现检索、认证等多种功能。在变换域实现版权保护有诸多优势,既可以和其他的图像处理同步进行,又可以充分兼顾到国际上通用的压缩标准算法。M.N.Do和M.Vetterli提出的有限脊波变换FRIT(Finite Ridgelet Transform)[1],由于在表示线奇异性表示方面有更好的优势,因此在图像去噪[2,3,8]、边缘检测[4]、版权保护[6]以及图像认证[5,7]等方面有许多研究与应用。
有限脊波变换首先通过“模运算”把Radon变换FRAT进行离散化处理,实现了图像二维的线奇异转化为一维的点奇异,然后通过DCT或者DWT等正交变换对点奇异进行处理,完成FRIT。FRIT比DWT具有更好的能量集中特性,在处理线奇异特征方面具有独特的优越性。
由于在FRAT算法中含有“模运算”,导致“环绕”现象的产生,影响了它在去噪、边缘检测、图像压缩、版权保护等图像处理方面更好的应用。因此,如何简便有效地去除“环绕”现象是急需解决的问题。
通过分析FRAT算法,找到了“环绕”现象的本质,结合图像的空间相关性,以及系数的软门限阈值处理算法,提出了一种去除“环绕”现象的简便方法。对于大小p=3图像,根据一定规则重排图像块系数,可以去除“环绕”现象,称之为改进的有限脊波变换MFRIT(ModifiedFiniteRidgeletTransform),并把MFRIT应用于版权保护算法。为了增强数字水印的鲁棒性,基于大能量准则,利用MAP选择大能量MFRIT系数,版权信息嵌入其中,实现版权保护。
1 有限脊波变换基本原理
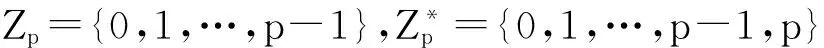
rk[l] =FRAT(k,l)
(1)
(2)
y0表示局部均值,定义为:
(3)
原始图像可以由下式重构:
(4)
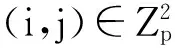
Pi,j={(k,l):l=j-ki(modp),k∈Zp}∪{(p,i)}
(5)
经过FRAT,一幅图像由直线特征转换到点特征,一幅p×p的图像变换成了一个p×(p+1)的系数矩阵期,第k列代表该斜率方向的FRAT系数,对每一列系数进行一维的DWT或者DCT处理,完成FRIT。
2 改进的有限脊波变换-MFRIT
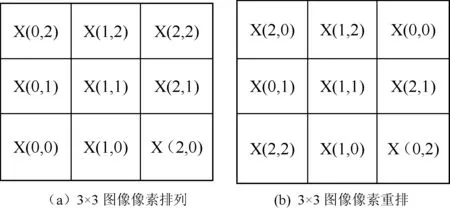
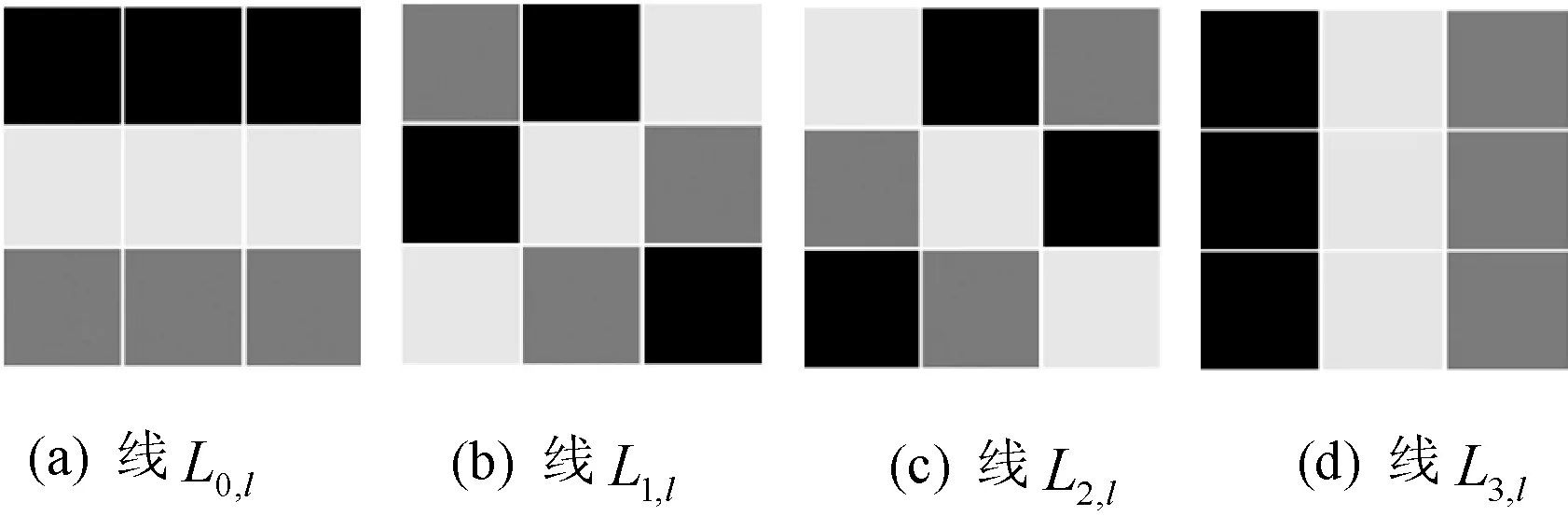
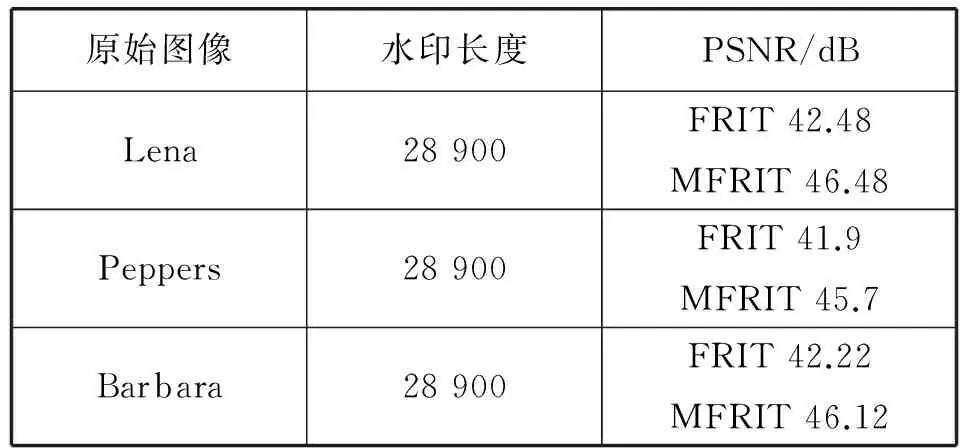
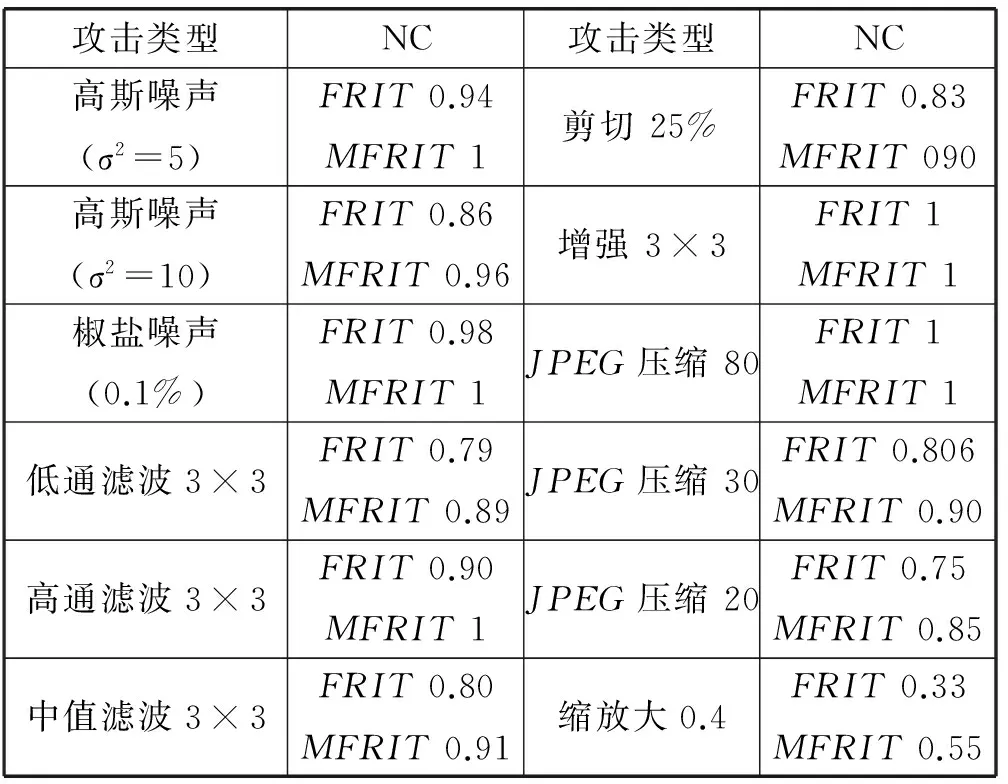
图1(a)表示的是3×3的图像像素集合x(i,j),0≤i,j≤2,FRAT处理后,它们组成了线的集合Lk,l,0≤k≤p,0≤l 式(1)中的直线由式(2)定义,其运用的模运算会导致FRAT的直线呈现出“环绕”现象。根据式(2)详细分析环绕现象的产生。 对于p=3时,则: k=0:L0,l={(i,j):j=l…(modp)} (6) l=0:L0,0={(i,j):j=0…modp} ={(i,j):(0,0),(1,0),(2,0)} l=1:L0,1={(i,j):j=1…modp} ={(i,j):(0,1),(1,1),(2,1)} l=2:L0,2={(i,j):j=2…modp} ={(i,j):(0,2),(1,2),(2,2) (7) l=0:L1,0={(i,j):j=i…(modp)} ={(i,j):(0,0),(1,1),(2,2)} l=1:L1,1={(i,j):j=i+1…(modp)} ={(i,j):(0,1),(1,2),(2,0)} l=2:L1,2={(i,j):j=i+2…(modp)} ={(i,j):(0,2),(1,0),(2,1)} k=2:L2,l={(i,j):j=2i+l…(modp)} 猪场寄生虫感染的发生和发展取决于多种因素:①猪圈被前批感染动物污染的程度;②畜舍环境条件是否有利于活虫量持续加大和(或)虫体的存活;③猪场中所存在的寄生虫的类型;④猪场的条件是否适合寄生虫通过直接接触的方式进行传播。 (8) l=0:L2,0={(i,j):j=2i…(modp)} ={(i,j):(0,0),(1,2),(2,1)} l=1:L2,1={(i,j):j=2i+1…(modp)} ={(i,j):(0,1),(1,0),(2,2)} l=2:L2,2={(i,j):j=2i+2…(modp)} ={(i,j):(0,2),(1,1),(2,0)} k=3:L3,l={(l,j):j∈Zp} (9) l=0:L3,0={(0,j):j∈Zp} ={(i,j):(0,0),(0,1),(0,2)} l=1:L3,1l={(1,j): ∈Zp} ={(i,j):(1,0),(1,1),(1,2)} l=2:L3,2={(2,j):j∈Zp} ={(i,j):(2,0),(2,1),(2,2)} 式(6)-式(9)所得数据构成图2。以上分析得知出现“环绕”现象的根本原因是存在着模运算。以此类推,当p为其它素数时也会出现环绕现象,而且数值越大,环绕现象越严重。但是对于p=3的情况,可以通过简便的方法去除“环绕”现象。基于相邻像素在空间上存在很强的相关性,对调对角像素的位置,如图1(b)所示,然后分别进行FRAT运算,依据文献[2]的方法对相关FRAT系数进行软门限阈值处理,可以去除“环绕”现象,称之为改进的FRIT(ModifiedFRIT-MFRIT)。对应的直线分布情况如图3(a)-(d)所示。正如图2(a)、(d)和图3(b)、(c)所示,解决了环绕现象。 (10) 图1 3×3图像像素排列情况 图2 图1(a)的FRAT直线 图3 图1(b)的FRAT直线 MFRIT有以下几个主要步骤: (1) 对于任意一幅图像(图像块),计算它的均值y0,然后图像的每个像素与均值y0相减。 (2) 对图像(图像块)分别进行FRAT变换,得到rk[l],其中,0≤k≤3,0≤l≤2。 (3) 按照图1(b)的规则重排图像(图像块)像素。 (6) 根据式(10)求得图像中心像素的预测值。 3.1MFRIT系数的提取 我们对大量标准图像进行MFRIT处理,对它们的系数进行统计分析,发现其分布规律与文献[5]类似,即MFRIT有能量集中特性,而且大能量系数主要集中分布在四个方向,分别为水平方向、垂直方向、135°方向和45°方向。图像的MFRIT系数分布符合拉普拉斯统计分布规律,如图4所示。大能量系数携带图像的主要信息,在一系列的图像处理过程中有更强的鲁棒性,因此,我们自适应地提取大能量的MFRIT系数,嵌入版权信息,实现版权保护。具体方法是把MFRIT系数设定为一个随机变量x(n),根据MAP准则,选取大能量系数。 图4 FRIT系数的分布图 为了提取大能量系数,设随机变量x(n)是叠加了白噪声的MFRIT系数: x(n)=s(n)+w(n) (11) (12) 设变量s(n)的Laplace分布为: (13) 根据最大后验概率估计定义,S的估计值为: (14) 对式(14)进一步取对数运算得: (15) 其中: (16) 把式(12)、式(16)代入式(15),并对s取导数,得到s的最佳估计: (17) 在实际应用中,对于一个N×N的图像,σw可以根据以下方法确定: (18) 根据式(11),可以得到: (19) 基于大能量原则,根据式(17)提取MFRIT系数,把水印版权信息嵌入其中,能够更好地抵抗攻击,提高水印算法的鲁棒性。携带水印信息的系数位置存储为Rt序列。对大量的标准图像和自然图像作了统计分析,训练Rt序列,得到大能量系数的位置序列R。该序列应用在发送端和接收端。 3.2 水印信息的嵌入和提取 水印信息的嵌入流程如图5所示。 图5 水印的嵌入流程图 使用可识别二值图像Iw作为水印信息,大小为M1×M2。表示为: Iw={w(i,j),0≤i 为了增强安全性,对水印Iw进行加扰处理,密钥为K1,表示为Iwz,用密钥K2从序列R中随机选取M1×M2个MFRIT系数,我们采用抖动调制技术嵌入水印[9],携信息的MFRIT系数映射到原来位置,进行逆MFRIT[1],得到嵌入水印的图像I′。 (1≤i≤M1,1≤j≤M2) (20) 针对同一幅图像,分别基于FRIT和MFRIT域,然后采用抖动调制技术嵌入了相同的水印信息,以便于说明FRIT“环绕”现象的影响。从不可见性和鲁棒性两方面对水印算法进行验证,采用峰值信噪比PSNR对图像进行客观评价。图6是基于MFRIT域的实验结果。图6(a)、图6(c)分别是原始灰度图像、含有水印的图像,大小为512×512,图6(c)的PSNR=46.48dB,主观视觉上察觉不到二者的差别,图6(b)是原始的水印信息,在本次试验中水印信息大小为170×170,图6(d)为提取的水印信息,其NC=1,视觉上二者没有任何差别,说明该算法具有良好的透明性。不同结果如表1和表2所示。部分攻击实验结果如图7所示。 图6 算法的有效性验证 原始图像水印长度PSNR/dBLena28900FRIT42.48MFRIT46.48Peppers28900FRIT41.9MFRIT45.7Barbara28900FRIT42.22MFRIT46.12 表2 水印图像经过不同攻击后的结果 图7 部分攻击实验提取的水印 通过分析FRAT算法,揭示了FRIT“环绕”现象和FRAT系数的关系,以此为基础,提出了一种去除环绕效应的改进算法MFRIT。依据拉普拉斯模型,应用MAP准则,自适应地选取了大能量MFRIT系数,把版权信息嵌入其中。实验结果显示,经过MFRIT处理的图像嵌入水印信息后有更强的鲁棒性和透明性。后续工作是把MFRIT算法应用于图像的去噪。 [1] Minh N Do,Martin Vetterli.The finite ridgelet transform for image representation[J].IEEE Transactions on Image Processing,2003,12(1):16-28. [2] Donoho D.De-noising by soft thresholding[J].IEEE Transactions.on Information.Theory,1995,41(5):613-627. [3] Wang Xin.Wrap-around effect removal finite ridgelet transform for multiscale image denoising[J].Pattern Recognition,2010,43(5):3693-3698. [4] 祝瑞玲,王欣,韩国栋.基于有限脊波变换的边缘检测算法[J].山东大学学报(工学版),2011,41(4):113-118. [5] 祝瑞玲,王欣.基于有限脊波变换的图像内容认证算法[J].光电子·激光,2009,20(8):1087-1091. [6] 朱银芳.一种基于脊波域的扩频水印盲检测方法[J].计算机应用与软件,2013,30(5):327-330. [7] Zhen Yao,Nusir Rujpoot.Radon/Ridgelet signature for image authentication[C]//Proceeding of International Conference on Image Processing,Singapore,2004:43-46. [8] Chen G Y,Kegl B.Image denoising with complex ridgelets[J].Pattern Recognition,2007,40(3):578-586. [9] Brian Chen,Gregory W Wornell.Digital watermarking and information embedding using dither modulation[C]//1998 IEEE Second Workshop on Multimedia Signal Processing,California:IEEE,1998:273-278. IMPROVED ALGORITHM FOR SOLVING WRAP-AROUND EFFECT OF FINITE RIDGELET TRANSFORM AND ITS APPLICATION IN COPYRIGHT PROTECTION Zhu Ruiling1Han Zhuoran2 1(DepartmentofInformationEngineering,ShandongCommunicationandMediaCollege,Jinan250200,Shandong,China)2(SchoolofElectronicInformationandElectricalEngineering,ShanghaiJiaoTongUniversity,Shanghai200240,China) Finite Ridgelet Transform (FRIT) can effectively represent linear singularities in image, thus it is widely used in various fields. However, the limitation of wrap-around effect restricts its applications in image processing. Since the relation between wrap-around effect and distribution of FRAT (Finite Radon Transform) coefficients has been revealed, an improved algorithm which can remove the wrap-around effect is proposed through the spatial correlation of pixels and processing the soft threshold of FRAT coefficients. Copyright information is embedded in the MFRIT (Modified Finite Ridgelet Transform) coefficients which are selected according to maximum a posterior (MAP) estimating principle. Experimental result proves the relatively robustness and transparency. Finite ridgelet transform Copyright protection Wrap-around MAP 2016-02-23。山东省高等学校科研计划项目(J12LN89)。祝瑞玲,教授,主研领域:图像处理与计算机视觉。韩卓然,本科生。 TP391 A 10.3969/j.issn.1000-386x.2017.04.056


3 水印的嵌入与提取
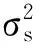
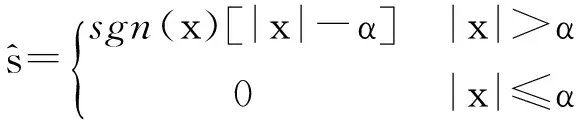
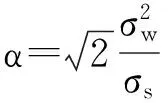
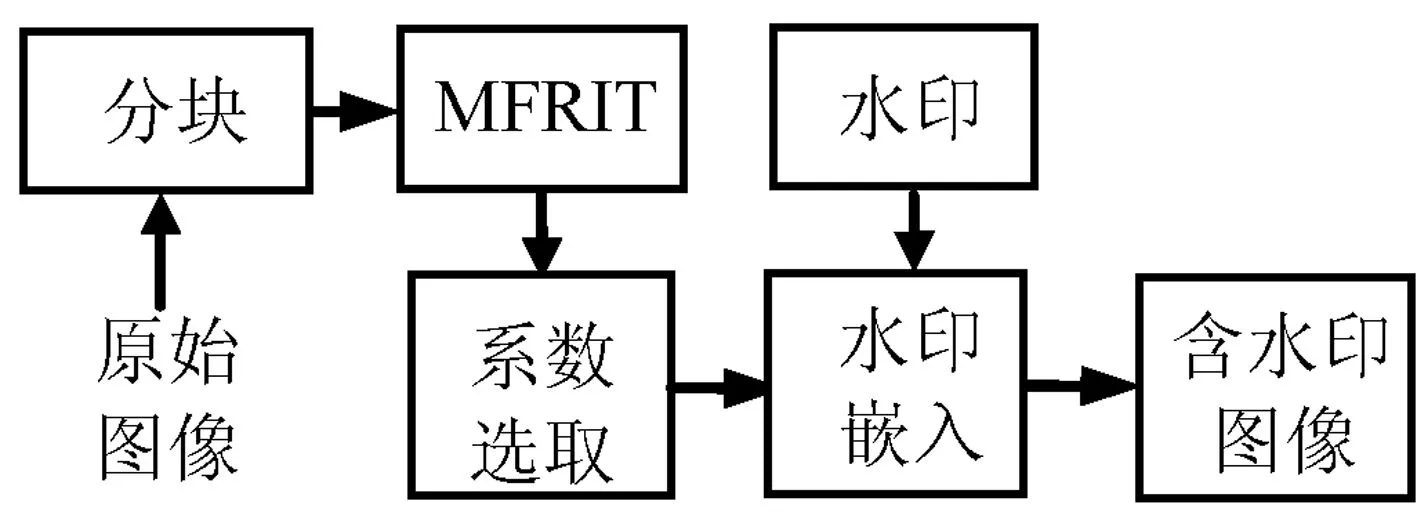
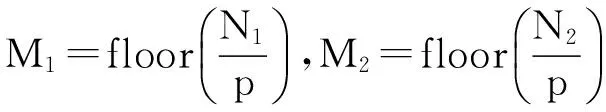
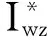
4 实验结果


5 结 语

