基于容差计算的非完备信息系统属性约简算法

梁 宝 华

(巢湖学院信息工程学院 安徽 合肥 238000)

基于容差计算的非完备信息系统属性约简算法

梁 宝 华

(巢湖学院信息工程学院 安徽 合肥 238000)

对于有缺损值的非完备信息系统约简，多数算法利用容差关系求信息量，但此类算法需消耗大量时间计算容差，导致属性约简质量、消耗的时间及空间复杂度均不理想。为了有效提高求容差类计算效率，引入一个与相容类信息量等价的计算公式。以此为基础，提出一种属性约简算法，使时间复杂度降为O(|C|2|U|)，空间降为O(|C||U|)。最后，通过实例和实验分析并验证了算法的有效性和可行性。

粗糙集 属性约简 非完备信息系统 相容类

0 引 言

粗糙集理论[1-2]是由波兰数学家Pawlak教授于1982年提出的，是一种处理不完全、不精确和模糊性数据的数学工具。属性约简是粗糙集理论研究的重要内容之一，指在不影响原知识表达能力的情况下，通过消除冗余属性的方法，从而获得较简洁的知识表达。经典的粗糙集理论在完备信息系统中已有大量的研究，提出了基于正区域、基于差别矩阵、基于信息熵及启发式属性约简算法[3-5,14-19]。然而在现实生活中，由于对数据的理解、获取方法的限制等不可控因素，使得实际处理的数据是一个不完备信息系统，即部分对象属性值是未知的。这种数据缺失会影响粗糙集理论向实用化方向推广。

为了解决不完备信息系统对粗糙集理论应用化的影响，研究者们利用相容关系[6]、相似关系等，给出一系列有效的属性约简算法，如文献[7]给出了差别矩阵的二进制形式,文献[8-10]提出相容关系相似矩阵并给出一种不完备决策表的属性约简算法。不完备决策表的属性约简算法多数以“信息量”[10]为启发式信息，张等在文献[11]中提出一些改进方法，经研究发现，文献[11]存在大量重复扫描数据对象的不足。为了减少扫描数据的次数，无需大量空间存储相容类信息，本文根据相容类元素间的对称性、自反性特征，提出一种快速计算相容信息量的方法，有效提高属性约简效率。最后通过实例及实验验证算法的有效性和正确性。

1 相关概念

设信息系统S=(U,A,V,f)，其中U为论域，A=C∪D，P⊆C，C为条件属性，D为决策属性；V是属性集A的值域；f是从属性到值域的映射。

定义1[5]若a∈C,且有f(x,a)=*(*为缺损值)，则称此信息系统是不完备的，否则称为完备信息系统。

定义2[6]由P决定的相容关系T为：

T(P) ={(x,y)∈U×U|∀a∈P,f(x,a)

=f(y,a)∨f(x,a)=*∨f(y,a)=*}

(1)

由T(P)定义可得相容类定义为：

TP(x)={y|y∈U∧TP(x,y)}

(2)

显然，相容类TP(x)满足自反性、对称性。

定义3[11]属性集P⊆C的信息量定义为：

(3)

其中U={x1,x2,…,xn},|X|为集合X的基数。

定义4[11]属性集B关于决策属性D的条件信息量定义为：

I(B|D)=I(B∪D)-I(B)

定义5[11]在不完备信息S中，属性a∈P⊆C的重要度定义为：

SigP(a)=I(P|D)-I((P∪{a})|D)

(4)

定义6[11]在非完备信息系统S中，属性P是C关于D的一个约简，则要同时满足下述两个条件：

(1)I(P|D)=I(C|D)

(2) ∀a∈P⟹I((P-{a})|D)≠I(C|D)

2 改进属性约简算法

2.1 相容类计算分析

在不完备信息系统的属性约简中，多数算法需计算信息量。由于计算方法的不当，消耗大量的时间和空间资源。如文献[9]计算信息量的思想是将每一对象与其他|U|-1个对象进行比较，这样若对属性集P求信息量，有大量重复的计算，文献[10]对其进行改进，时间大约只需文献[9]同等条件下的一半。

现通过实例说明如下，设有一不完备决策表，如表1所示。

表1 不完备决策

Ta1(1)={1,2,4,7}Ta1(2)={1,2,4,7}

Ta1(3)={3,4,5,7}Ta1(4)={1,2,3,4,5,6,7,8}

Ta1(5)={3,4,5,7}Ta1(6)={4, 6,7,8}

Ta1(7)={1,2,3,4,5,6,7,8}Ta1(8)={4, 6,7,8}

T{a1,a2}(1)={1,2,4,7}=T{a1,a2}(2)

T{a1,a2}(3)={3,4,5,7}=T{a1,a2}(5)

T{a1,a2}(4)={1,2,3,4,5,6,7,8}=T{a1,a2}(7)

T{a1,a2}(6)={4, 6,7,8}=T{a1,a2}(8)

T{a1,a2,a3}(1)={1,2}T{a1,a2,a3}(2)={1,2}

T{a1,a2,a3}(3)={3,4,5,7} T{a1,a2,a3}(4)={3,4,5,7}

T{a1,a2,a3}(5)={3,4,5,7}T{a1,a2,a3}(6)={6}

T{a1,a2,a3}(7)={3,4,5,7}T{a1,a2,a3}(8)={8}

根据以上计算相容类过程，发现计算相容类T(P)时，出现大量的重复比较， 可总结为以下几点性质：

性质1TP(x)中所有对象在属性集上取值均属于不可区分对象。

证明：TP(x)中所有元素均为与x样本在属性P的取值相等，即x与TP(x)中所有其他元素在属性P上不可区分，证毕。

性质2TP(x)⊇TP∪ai(x),ai∈C-P

证明：对于∀y∈TP∪ai(x)，根据相容类定义可知，y与TP∪ai(x)中的所有元素无不可区分，由于P⊆(P∪ai)，所以，y与TP(x)上所有元素也均不可区分，即y∈TP(x)，因为y具有任意性，TP(x)⊇TP∪ai(x)，证毕。

性质3 若|U/ai|=1或|U/ai|=2且对象在属性ai上取值有*的，则TP(x)=TP∪ai(x)。

证明：因为|U/ai|=1，即所有样本在属性ai上取值相同，即Tai(x)=U。对于∀y∈TP(x)，有y与TP(x)中所有元素在属性P均不可区分。所以必有y在属性P∪ai都不可区分，即，y∈TP∪ai(x)。因为y具有任意性，所以得到若|U/ai|=1且∀y∈TP(x)时，y∈TP∪ai(x)，即TP(x)⊆TP∪ai(x)。又由性质2可得TP(x)⊇TP∪ai(x)，所以得TP(x)=TP∪ai(x)。|U/ai|=2且在属性ai上取值有缺损值，由于缺损值与其他所有样本在ai上均不可区分，所以等价于|U/ai|=1的情况，证毕。

2.2 改进相容类计算方法

由于相容类具有自反性、对称性，所以信息量计算时，存在大量的重复性计算，为了避免这一现象的发生，现定义信息量Inf(P)如下：

信息量计算分析如下：

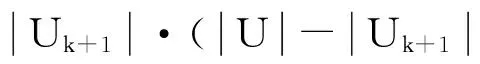
(5)

性质4Inf(P)与定义3I(P)信息是等价的。

(6)

算法1 改进相容类计算：Inf(P∪ai)且ai∈C-P

输入：不完备信息表S=(U,A,V,f),Inf(P),ai

//在相容类计算过程中,U不断剪枝成U′

输出：Inf(P∪ai)

intInfP( )

{

sum= 0;

将所有样本按属性P进行划分;

{

else

deleteU/PifromU

}

ifexistssubsetof*then

returnsum;

}

2.3 新的属性约简算法

定义7 在不完备信息系统S中，属性P关于决策属性D的条件信息量为：

Inf(P|D)=Inf(P)-Inf(P∪D)

(7)

定义8 在不完备信息系统S中，属性b关于属性组B的重要程度为：

(8)

性质5Inf(P)的值越大，区分能力越弱，当Inf(P)=0时，此时的P即为所求的属性约简集。

算法2 新的属性约简算法

输入：U,C,D

输出：Core//属性约简集

Step1 U=U′,Core=∅,C′=C；

Subset=∅;SubsetD=∅

//Subset存储U在条件属性下的子划分

//SubsetD存储U在决策属性下的划分；

Step2 计算C′中每个条件属性在决策属性D下的条件信息量Inf(Ci∪Core|D)，并选出最小的信息量对应的条件属性Ck;

Core=Core∪Ck

Subset=U/Ck;SubsetD=U/Core∪D;

C′=C-Ck；

Step3 if (C′≠∅∧Inf(Core|D)≠0)

转Step2；

Step4 return Core

3 实例与实验分析

3.1 属性约简实例

以表1的数据为例，求U在各条件属性上的划分为：

U/a4={{1,3,6,7,8},{2,4,5}}

其中带下划线的一组为缺损值，所以各条件属性的信息量分别为：

同理，相对各条件属性在决策属性D下加细划分分别为：

U/(a4∪D)={{1,7},{2,4,5},{3,8},{6}}

其对应的信息量为：

Inf(a1∪D)=8,Inf(a2∪D)=11

Inf(a3∪D)=7,Inf(a4∪D)=5

则：

由于a1与a4的值最小，所以区分能力最强，设选择属性a1加入Core中得Core={a1}，舍弃基数为1的子划分，所以Subset={{1,2},{3,5},{6,8},{4,7}},SubsetD={{1,2},{5},{4,7}}。继续加入其他属性并进行加细得：

U/(Core∪{a3}∪D)={{1,2},{5,4,7}}

U/(Core∪{a4}∪D)={{1,7},{2,4},{4,5}}

3.2 实验分析

为了比较同类算法与本文算法的约简效果，实验使用的硬件配置为：Intel®CoreTMi7-4712MQ,CPU主频2.30GHz,4GB内存，软件为Win7系统及VS2012平台。实验采用UCI数据库中的9个数据集进行验证，数据集分别为Post,Zoo,Hepatilis,AutoMPG,Dermatologh,Car,Chess,Mushroom,Nursery(为方便描述表格中分别用D1～D9表示)，具体数据描述如表2所示，表2中的Data为各类数据集名称，|U|为样本数，|C|为条件属性数，NO为分类数，DataType为数据类型，Comp为是否完备性。

表2 UCI数据集

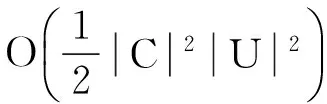
表3 三种算法约简效果表

续表3

Data算法b算法cTimeSpaceRLbTimeSpaceRLcD10.01930.000980.01610.00098D20.02060.008350.01840.00835D30.18990.014560.18220.01456D40.29010.016250.20140.01625D50.21460.012170.17030.01217D60.40810.011560.38900.01156D71.88340.1227291.07520.122729D81.64280.180440.93150.18044D91.78530.102881.03230.10288

(1) 从表3的实验数据可以看出，以上三种算法在约简质量上，与常见约简算法的结果相当，说明这种约简算法是有效可行的。算法a对于数据集Zoo,Dermatologh,Chess约简结果稍微有点偏差，很明显算法b和算法c的约简结果更具有准确性。

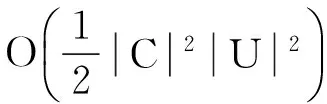
(3)Post是非完备的，Zoo具有完备性，虽然Zoo的样本多且属性也多，由于Post是非完备数据集，对于那些缺损值增加了挖掘的干扰，对于算法a增加了信息量的计算，但对算法b、算法c的属性重要性计算影响不大。所以，在进行约简时数据集Post虽然比Zoo样本数及属性个数少，但约简时却与Zoo的相仿佛。

(4) 从时间性能上看，算法b和算法c明显优于算法a，通过表3的运行时间长短可看出。算法b与算法c整体差不多，但算法c要略优于算法b，因为算法b需计算正区域，所以要浪费一定的时间，当然，随着数据集样本数及属性数的增多，这段时间占整个约简的比例会越来越小。

4 结 语

[1]PawlakZ.Roughsettheoryanditsapplicationstodataanalysis[J].CyberneticsandSystems,1998,29(7):661-668.

[2]PawlakZ,Grzymala-BusseJ,SlowinskiR,etal.Roughsets[J].CommunicationsoftheACM,1995,38(11):88-95.

[3] 徐章艳,刘作鹏,杨炳儒,等.一个复杂度为max(O(|C||U|),O(|C|2|U/C|))的快速属性约简算法[J].计算机学报,2006,29(3):391-399.

[4] 张文修,米据生,吴伟志.不协调目标信息系统的知识约简[J].计算机学报,2003,26(1):12-18.

[5] 王国胤,于洪,杨大春.基于条件信息熵的决策表约简[J].计算机学报,2002,25(7):759-766.

[6] 王国胤.不完备信息系统的粗糙集扩展[J].计算机研究与发展,2002,39(8):1238-1243.

[7]McBrienP.Temporalconstraintsinnon-temporaldatamodellinglanguages[C]//27thInternationalConferenceonConceptualModeling,Barcelona,Spain,2008:412-425.

[8]ZhouJ,XuE,LiY,etal.Anewattributereductionalgorithmdealingwiththeincompleteinformationsystem[C]//2009InternationalConferenceonCyber-EnabledDistributedComputingandKnowledgeDiscovery,2009:12-19.

[9] 黄兵,周献中,张蓉蓉.基于信息量的不完备信息系统属性约简[J].系统工程理论与实践,2005,25(4):55-60.

[10] 李艳红,鄂旭,周津,等.信息量的不完备信息系统属性约简方法[J].小型微型计算机系统,2012,33(3):641-645.

[11] 张清国,郑雪峰,张明德,等.信息量不完备决策表属性约简的一种新算法[J].计算机工程与应用,2010,46(2):19-21,33.

[12] 谢娟英,李楠,乔子芮.基于领域粗糙集的不完整决策系统特征选择算法[J].南京大学学报(自然科学),2011,47(4):383-390.

[13] 纪霞,李龙澍,齐平.基于属性分辨度的不完备决策表属性约简算法[J].华南理工大学学报(自然科学版),2013,41(1):83-88.

[14] 冀素琴,石洪波,吕亚丽.基于粒计算与区分能力的属性约简算法[J].模式识别与人工智能,2015,28(4):327-334.

[15] 葛浩,李龙澍,杨传健.基于相对分辨能力的属性约简算法[J].系统工程理论与实践,2015,35(6):1595-1603.

[16] 陈宸,赵军.一种新的基于二进制分辨矩阵的属性约简方法[J].计算机应用与软件,2013,30(9):123-127.

[17] 马垣.形式概念中的内涵亏值及属性约简[J].模式识别与人工智能,2013,26(12):1096-1105.

[18] 杨春林.基于信息熵的属性约简在多属性决策中的应用[J].数学的实践与认识,2013,43(3):97-102.

[19] 王世强,张登福,毕笃彦,等.基于模糊粗糙集和蜂群算法的属性约简[J].中南大学学报(自然科学版),2013,44(1):172-178.

ATTRIBUTE REDUCTION ALGORITHM FOR INCOMPLETE INFORMATION SYSTEM BASED ON TOLERANCE COMPUTATION

Liang Baohua

(InformationEngineeringInstitute,ChaohuUniversity,Hefei238000,Anhui,China)

For incomplete information system reduction with defective values, most algorithms use the tolerance relation to compute the amount of information, but this kind of algorithm consumes a large amount of time computing tolerance, which leads to the quality of attribute reduction and the time and space complexity are not ideal. In order to improve the computation efficiency of the tolerance class effectively, a formula for calculating the equivalent information of the compatible class is introduced. Based on it, an attribute reduction algorithm is proposed, which reduces the time complexity to O(|C|2|U|)andreducesthespacetoO(|C||U|).Finally,theexamplesandexperimentalanalysisshowthattheproposedalgorithmisefficientandfeasible.

Rough set Attribute reduction Incomplete information system Compatible class

2016-03-30。安徽省省级质量工程项目(2013tszy31)；安徽省高等学校省级自然科学研究项目(KJ2013Z231)。梁宝华，副教授，主研领域：粗糙集，数据挖掘。

TP

ADOI:10.3969/j.issn.1000-386x.2017.04.051