基于加权秩和比法的铁路线路方案优选
刘慧群 李欣阳
(1.兰州交通大学土木工程学院,甘肃 兰州 730000; 2.兰州交通大学自动化与电气工程学院,甘肃 兰州 730000)
基于加权秩和比法的铁路线路方案优选
刘慧群1李欣阳2
(1.兰州交通大学土木工程学院,甘肃 兰州 730000; 2.兰州交通大学自动化与电气工程学院,甘肃 兰州 730000)
针对铁路线路方案优选没有统一的综合评价方法的现状,提出了基于秩和比法进行线路方案优选,利用秩和比法或者加权秩和比法确定各方案的概率单位,将其作为自变量代入回归方程,根据结果对各方案进行排序和分档,结果显示,运用秩和比法所选方案和其他方法所选方案以及设计院最终所拟方案一致。
铁路线路,方案优选,秩和比法,权重,熵值法
铁路选线是铁路设计阶段的第一个需要解决的重要问题,它关系到整个铁路设计的投资、质量、工期以及以后的功效而且也会影响到铁路沿线的经济发展和乘客及货物的运输[1]。除此之外,不同的线路方案对于当地的环境影响也有很大不同,目前国家大力发展环境友好型、资源节约型社会。铁路线路的优选必须要符合对资源的尽量节约,以及对于环境的破坏要尽量的减小。所以,在铁路设计的选线方案必选阶段,在保证可行性和质量安全的前提下,必须对于各个线路方案进行综合性地优选,从而使选出的最终方案是满足各方需求的最优方案。在进行铁路线路方案优选过程中主要考虑的指标因素有:线路长度、征地面积、投资总额、对当地发展的促进作用、噪声影响、环境影响、对既有线路的干扰等等的指标因素,其中有很多的定性指标,对于定性指标采用模糊数学进行赋权,对其进行分级即优、良、中、差、劣,其赋值分别对应0.9,0.7,0.5,0.3,0.1[2-4]。目前应用于线路方案优选的方法有灰色关联分析法、TOPSIS法、ELECTRE法、层次分析法等等[5-8],但各有利弊,在学科内未有统一的综合评价方法。针对于此,本文引入秩和比法进行铁路线路综合比选。秩和比法在医疗卫生和一些其他的统计学领域有着广泛的应用。其在工程领域才刚刚开始发展。在铁路线路方案优选的过程中,不能仅仅依靠主观判断指标重要程度来进行指标的赋权。这样往往不够准确与科学。为了克服主观赋权法所带来的不可避免的误差,本文引进客观赋权法中的熵值法[9]进行指标的赋权。再将所附的权值代入到秩和比法中进行综合评价,使得优选的方案科学、合理。
1 加权秩和比法
1.1 秩和比法原理
秩和比法[10]是一种广泛应用于统计学、医学的方案优选方法,其1988年被我国著名统计学家田凤调教授所提出,其中心思想是通过对矩阵里的秩进行转换从而得到一种新的没有量纲的统计量——RSR。然后比较方案的SRS,其越大则证明其越优,反之亦然。RSR法有如下优点:
1)其思路清晰,方法简单且计算量很小。
2)其对于方案的原始材料和数据要求很低,适合于各个领域。
3)通过进行编秩,可以消除非正常值的影响。
4)RSR因为没有量纲,方便做综合评价。
5)最终能对方案进行分档。
1.2 比选步骤
1.2.1 构建初始的评价矩阵
假设备选方案有m,记为M=(M1,M2,…,Mn),方案有n个指标,E=(E1,E2,…,En),方案Mi对于指标Ej的评价集合记为:aij(i=1,2,…,m;j=1,2,…,n),aij构成矩阵A。
1.2.2 编秩
对于原始评价矩阵的编秩是秩和比法进行方案优选的重要一环,在编秩之前一定要区分好指标是大优型还是小优型。对于大优型的指标适宜从小往大进行编秩,把量值最小的指标的秩看作1,最大的看作m,如果遇见量值相同的两个方案,那么取平均值作为其秩。对于小优型指标适宜从大往小进行编秩,量值最大的编秩为1,最小的为m,同样,对于量值相同的方案时,取其平均值作为其秩。这样就能够得到方案集的秩矩阵Rij。
1.2.3 求取方案的秩和比
秩和比记为RSR。
(1)
对于考虑加权的秩和比法,其最终的判断依据应该是基于加权的秩和比秩,其计算公式如下:
(2)
其中,wj为指标的权重值。
1.2.4 计算概率单位

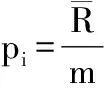
(3)

(4)
probiti=u(pi)+5
(5)
其中,u( )为标准正态下的离差函数。
1.2.5 计算回归方程
以概率单位probit自变量,以通过回归计算的秩和比或者加权秩和比估计值RSR***作为因变量,计算回归方程:
RSR***=a+bprobit
(6)
其中,a,b均为系数。
1.2.6 计算回归后的秩和比或者加权秩和比并进行分档
分档的依据是标准正态离差,其对应的probit如表1所示,根据各档的方差一致为最佳分档的原则,确定分档数。确定分档后,按照回归方程计算其临界值,从而进行分档。

表1 常用分档情况下的概率单位的临界值
2 赋权步骤
2.1 构建初始决策矩阵
假设备选方案集合记为:
M=(M1,M2,…,Mm)。
方案指标集合为:
E=(E1,E2,…,En)。
方案Mi对于指标Ej的评价集合记为:
(1) 大双边供电模式下4列AW0车同时起动电流峰值(4 000 A)未达到电流速断保护的整定值(9 000 A);
aij(i=1,2,…,m;j=1,2,…,n)。
aij构成矩阵A。
2.2 对于决策矩阵进行标准化
对于大优型指标利用式(7)进行标准化:
(7)
对于小优型指标利用式(8)进行标准化:
(8)
2.3 计算第j个指标第i个方案的特征比重
第j个指标第i个方案的特征比重pij表示第j个指标下,第i个方案的贡献度其可以按式(9)进行计算:
(9)
所有方案(m个方案)对指标j的贡献总量可以用熵来表示,熵的计算按照式(10)进行计算:
(10)
其中,K为常数,通常取1/lnm,对于某个特征中比重为0时,我们规定对于pij=0时,lnpij=0。
2.5 求取差异系数
从以上的过程可以看出指标的权值是由所有的方案之间的差异性来决定的。所以,可以定义差异系数来表达第j个指标下各方案贡献度的一致程度。其可以由式(11)进行计算:
gj=1-ej
(11)
2.6 求取各指标的权重
对于各指标的熵权重可以由式(12)进行计算:
(12)
3 算例分析
某铁路线路备选方案的具体数据见表2,其中,客运线路长度,征地面积,投资金额为小优指标,促进当地经济发展作用、对既有线的干扰,对环境的影响,噪声大小,对人民出行的影响等定性指标,经过量化后,变为大优型指标,根据上文方法,计算的权重向量如下:w=[0.080 5,0.076 1,0.082 8,0.181 4,0.098 1,0.196 2,0.186 7,0.098 1]。利用加权秩和比法的计算结果如表3所示。
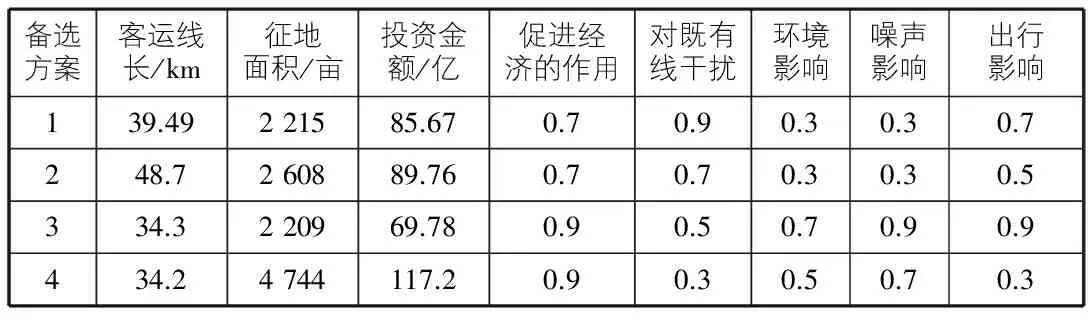
表2 备选方案评价数据

表3 编秩结果和加权秩和比
通过计算将百分率换算为概率单位,通过MATLAB计算回归方程为:
RSR***=0.181 3probit-0.376 4
(13)
计算结果如表4所示。根据加权秩和比回归方程计算得出的修正加权秩和比越大,方案越优。加权秩和比法、TOPSIS法以及灰色关联分析法对本算例的计算结果见表5。

表4 加权秩和比分布

表5 各备选方案的综合评价值
以上3种评估方法都是依据综合指数大小来进行方案优选且得到的优劣顺序一致。从优到劣的排序均是方案3>方案4>方案1>方案2。加权秩和比法的优势在于其不仅能够在备选方案中找到最优方案,其还能够对所有的备选方案进行分档比较,确定备选方案的等级数目以及线路方案备选方案所在的等级。
根据分档的方差一致的原则,就可以将所有的备选方案分成四档:优、良、可、差。根据表1中的分档界限值以及计算出来的RSR***来确定备选方案所处的等级。查表1可知当分四档时probit的临界值是3.5,5,6.5 。按照上文计算的回归方程来计算加权秩和比的临界值。计算结果如表6所示。对于本次4个备选方案,方案3属于优的等级,方案1,4属于良的等级,方案2属于可的等级。
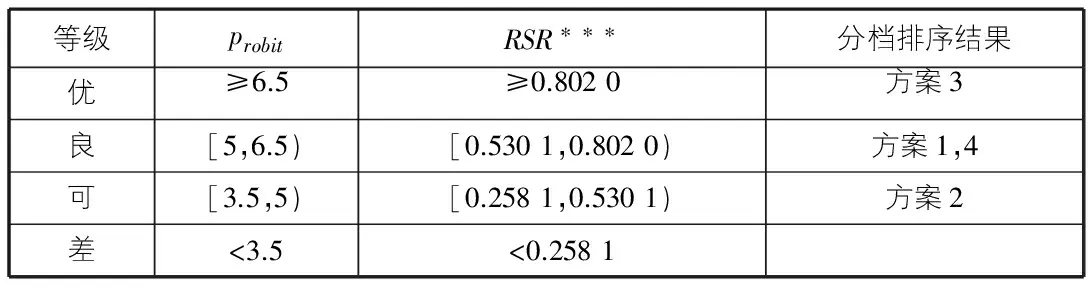
表6 计算结果
4 结语
基于铁路建设的线路方案优选问题,本文建立了一种新型评价方法——基于加权的秩和比法。在确定各个指标权重时,利用客观赋权法——熵值法,来尽量减小主观影响。最终将铁路线路优选问题量化为求取加权秩和比的问题。通过和工程中常用的优选方法灰色关联分析法和TOPSIS法进行比较,其最终排序结果完全相符,且和设计院最终所选方案一致。加权秩和比法具有方法简单,计算量小,其结果不仅能够从备选方案中找到最优方案,还能逐个对备选方案进行分等级评价等优点。所以,加权秩和比法是可以应用于铁路线路方案优选的方法,且效果明显。
[1] 易思蓉.线路工程信息技术[M].成都:西南交通大学出版社,2007.
[2] 易思蓉.铁路选线设计[M].成都:西南交通大学出版社,2007.
[3] 薛丽娜.铁路客运专线建设项目经济评价方法研究[D].成都:西南交通大学,2004.
[4] 王海霞.铁路建设项目经济评价若干问题的探讨[J].铁道运输与经济,2000(9):30-32.
[5] 曹明霞.灰色关联分析模型及其应用研究[D].南京:南京航空航天大学,2007.
[6] 付巧峰.关于TOPSIS法的研究[J].西安科技大学学报,2008,28(1):190-193.
[7] 朱建军.层次分析法的若干问题研究及应用[D].沈阳:东北大学,2005.
[8] 邱 东.多指标综合评价方法的系统分析[M].北京:中国统计出版社,1991:56-89.
[9] 陈华友.熵值法及其在确定组合预测权系数中的应用[J].安徽大学学报(自然科学版),2003.
[10] 田凤调.秩和比法及其应用[M].北京:人民卫生出版社,2002.
Optimization of railway route scheme based on weighted Rank Sum Ratio
Liu Huiqun1Li Xinyang2
(1.CivilEngineeringCollegeofLanzhouJiaotongUniversity,Lanzhou730000,China;2.SchoolofAutomationandElectvicalEngineering,LanzhouJiaotongUniversity,Lanzhou730000,China)
According to the incomplete comprehensive eraluatiion method for the optimal selection for the railway route schemes, route scheme optimization based on Rank Sum Ratio(RSR) method is used in this paper. Determine the probability units of each scheme by RSR method or weighted RSR method, then take them as independent variables into the regression equation, sort and distribute the programs according to the results. The result shows that select scheme in using RSR method is the same as the scheme selected by other methods and the final plan protocoled by design institute.
railway line, scheme optimization, RSR, weight, entropy method
1009-6825(2017)05-0169-03
2016-12-07
刘慧群(1990- ),男,在读硕士; 李欣阳(1990- ),男,在读硕士
U212
A

