基于SG/Simulink的一种改进MPPT算法

王海燕，秦 健，王旭佳

(上海电力学院 自动化工程学院，上海200090)

基于SG/Simulink的一种改进MPPT算法

王海燕，秦 健，王旭佳

(上海电力学院 自动化工程学院，上海200090)

针对传统MPPT算法响应速度慢和追踪精度不够理想的特点，分析了光伏电池在不同环境下的输出特性，提出一种改进的变步长扰动观测法，即采用新的自适应步长公式 作为扰动步长，使光伏电池以较大步长快速接近最大功率点，然后以较小步长稳定于最大功率点。在SG/Simulink混合建模仿真平台下进行了仿真，所得结果表明算法可显著提高最大功率点追踪速度与精度。

MPPT；扰动观测(P&O)法；System Generator(SG)

太阳能作为一种清洁能源，在人类面临化石能源枯竭、环境污染日益严重的情况下，成为许多国家大力发展的新兴能源，将太阳能转化为电能，利用太阳能电池板进行光伏发电成为一种行之有效的方式[1]。

最大功率跟踪(MPPT)控制技术是太阳能光伏发电中最主要的控制技术之一。目前常见的MPPT控制方法主要包括恒压(CV)法[2]、扰动观测(P&O)法[3]、增量电导(INC)法[4]等,其中扰动观测法具有算法结构简单、硬件实现容易的特点，因而得到了广泛的应用。本文在研究分析传统扰动观测法的基础之上，提出一种改进的扰动观测法，并以FPGA作为硬件实现平台，通过SG/Simulink混合仿真对改进算法的有效性进行验证。

1 光伏电池的特性

1.1 光伏电池数学模型

太阳光照射光伏电池时，由于光生伏特效应， 光伏电池将太阳辐射能转化为电能。光生伏特效应的本质是利用半导体的PN结特性实现能量转换，因此光伏电池的等效模型可以采用单二极管的等效电路模型来描述[5-6]，其等效电路模型如图1所示。

图1 光伏电池等效电路模型

其中，恒流源Iph与二极管D并联；Rp和Rs分别表示电池内部的串联和并联电阻。将温度与光照两个影响光伏电池输出特性的重要变量作近似处理，恒流源Iph的值等于光伏电池的短路电流。光伏电池的的I-V特性方程为

(1)

P-V特性方程为

(2)

式中，Iph为光生电流；I0为反向饱和电流；U为光伏电池输出电压；q为电荷常数，取值为1.6×10-19eV；K为玻尔兹曼常数，取值为1.38×10-23；T为系统工作温度；A为二极管理想品质因数。

1.2 光伏电池输出特性

光伏电池输出特性主要受光照强度、光伏电池温度两个变量的影响，根据光伏电池的数学模型，应用Matlab/Simulink搭建模型进行仿真，图2为光伏电池温度保持25 ℃，改变光照强度后得到的P-U曲线。图3为光照强度保持1 000 W/m,改变光伏电池温度后得到的P-U曲线。

图2 不同光照强度下光伏电池P-U曲线

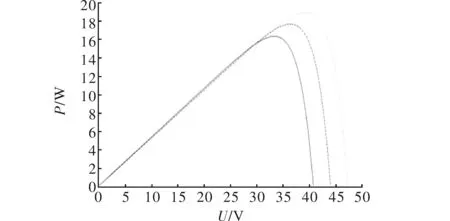
图3 不同温度下光伏电池P-U曲线

从以上仿真曲线可以看出，太阳能光伏电池是一种典型的非线性元件，在不同的温度、光照下，可以输出不同的电压，且其输出功率随输出电压的升高先升后降，因此存在输出功率最大点，即最大功率点。

2 新型扰动观测(P&O)法

光伏组件与负载间通常由直流变换电路(DC-DC)相适配，本文选用Boost电路作为直流升压变换电路，Boost电路的输入、输出电压关系为

Upv=U0(1-D)

(3)

式中，Upv为光伏阵列输出电压；U0为Boost电路输出电压；D为Boost电路中IGBT的占空比。

光伏并网发电系统中逆变电路控制Boost电路输出电压恒定，即U0值不变。由式(3)知，调节占Boost电路空比D，可以改变光伏组件的输出电压，从而使光伏电池输出电功率稳定在最大功率点。

2.1 传统扰动观测法

传统扰动观测法主要为定步长扰动观测法，其原理为：每隔一段时间以固定的步长ΔD扰动Boost电路占空比D，观测前后功率的变化方向，根据功率的变化方向，决定下一时刻的扰动方向。由图2～图3光伏电池的P-U特性曲线可知：最大功率点左侧dP/dV>0，应减小占空比D；最大功率点右侧dP/dV<0，应增大占空比D；最大功率点处dP/dV=0，D保持不变。传统扰动观测法算法简单、易于硬件实现，但追踪速度较慢，且输出功率在最大功率点处振荡较大，因此造成了光伏电池输出功率的损失。

2.2 改进的扰动观测法

针对传统扰动观测法中存在的问题，文献[8]提出以固定电压启动，通过观测dp数值大小来划分步长的扰动观测法。该算法实质上是一种定步长算法，虽然能获得低振幅的输出功率，但追踪最大功率点的速度较慢，原因在于算法的扰动步长是固定的，追踪效果受切换步长的判定区间影响较大。文献[7]采用变步长的扰动观测法，由变步长计算公式Step=kΔP/ΔV确定算法的扰动步长，相较于文献[8]能获得更快的MPPT追踪速度，但硬件实现时，由于引入除法运算，会占用较多的FPGA逻辑资源与机器周期，降低算法在硬件上的行速度。

因此本文提出一种改进的变步长扰动观测法，并定义新的自适应步长公式为

Step=N×(dV·dP)

(4)

式中，N为正数，即变步长速度因子，用于调整步长的变化速度。同时，根据式(4)可以构造电压扰动表达式

Vref=Vref+Step=Vref+N×(dV·dP)

(5)

式中，dV·dP的符号与dV/dP一致，即光伏电池工作在最大功率点左侧时，Step为正数，输出电压Vref不断增大；光伏电池工作在最大功率点右侧时，Step为负数，输出电压Vref不断减小；光伏电池工作在最大功率点时，Step为零，输出电压Vref稳定不变。对应到图2～图3中光伏电池的P-U特性曲线上，光伏电池的输出功率总是朝最大功率点移动，并最终稳定于最大功率点。

改进的变步长扰动观测法的控制策略为：每隔一段时间计算 |P(k)-P(k-1)|的值，ε为接近于零的很小的数，若|P(k)-P(k-1)|的值>ε，则由式(5)自适应的更新扰动步长Vref，若|P(k)-P(k-1)|的值小于常数ε则跟新P(k),V(k),然后结束返回。算法流程如图4所示。

图4 改进的变步长扰动观察法算法流程图

3 SG建模

System Generator(SG)是Xilinx公司开发的Matlab/Simulink环境下的一个工具箱，它可在Matlab/Simulink的环境下建立数字信号处理系统的抽象算法，并将抽象算法转化成可靠的硬件实现[9]。

SG的使用方法与Simulink中其它库的使用方法相类似，只要将所需的模块放置到编辑区进行设计即可。但由于SG库要用于生成VHDL代码，所以它和其它的Simulink库又有所不同[10]。首先，SG中处理的是定点数运算。大多数Simulink模块使用双精度浮点数进行运算并输出，因此需要使用Gateway In模块将浮点数转换成定点数，以实现SG与Simulink之间的无缝整合。其次，SG中的模块只能以固定的步长运行。它的每个步长代表FPGA中的一个时钟周期，但它并不是FPGA的实际工作频率。

为验证改进扰动观测法在不同环境条件下追踪最大功率点的快速性和稳定性，在Matlab/Simulink中利用SG工具箱搭建算法仿真模型如图5所示。

模型中主要包括光伏电池(PV)模块、MPPT模块、PWM模块和Boost升压电路模块,设计PV模块时，为简化结构、增强实用性，选择搭建基于外特性模型的光伏电池Simulink模型[11-12]。

根据上述改进扰动观测法的基本原理，选择SG工具箱中的基本模块组合成MPPT模块，如图6所示。

图6 SG组建的MPPT模块

设计的MPPT模块中主要包括乘法器、加法器以及寄存器，由于改进扰动观测法采用了新的变步长计算公式，因此省略掉了判断dV是否为0的分支，用乘法运算代替了除法运算，这样整个模块结构变得更简单且硬件实现时占用FPGA资源更少。

MPPT模块中处理的数据均为定点数。在选择定点数位宽时，所取的位宽越长，能表示数值范围越大，精度也越高，但这样会消耗更多的硬件资源，降低算法的运行速度。考虑到光伏电池输出电压、电流和功率数值的范围较小，将定点数的位宽设置为32位，1位符号位、15位整数位和16位小数位，是足够的。

4 仿真结果及分析

运行基于SG/Simulink混合建模法搭建的改进扰动观察法仿真模型。设置SG仿真步长为0.001 s，采样周期为0.001 s，选用的FPGA芯片型号为XC6SLX150T-2FGG484。在标准状况下：T=25 ℃，S=1 000 W/m2,步长速度因子N分别取0.005和0.001，其仿真结果如图7所示。

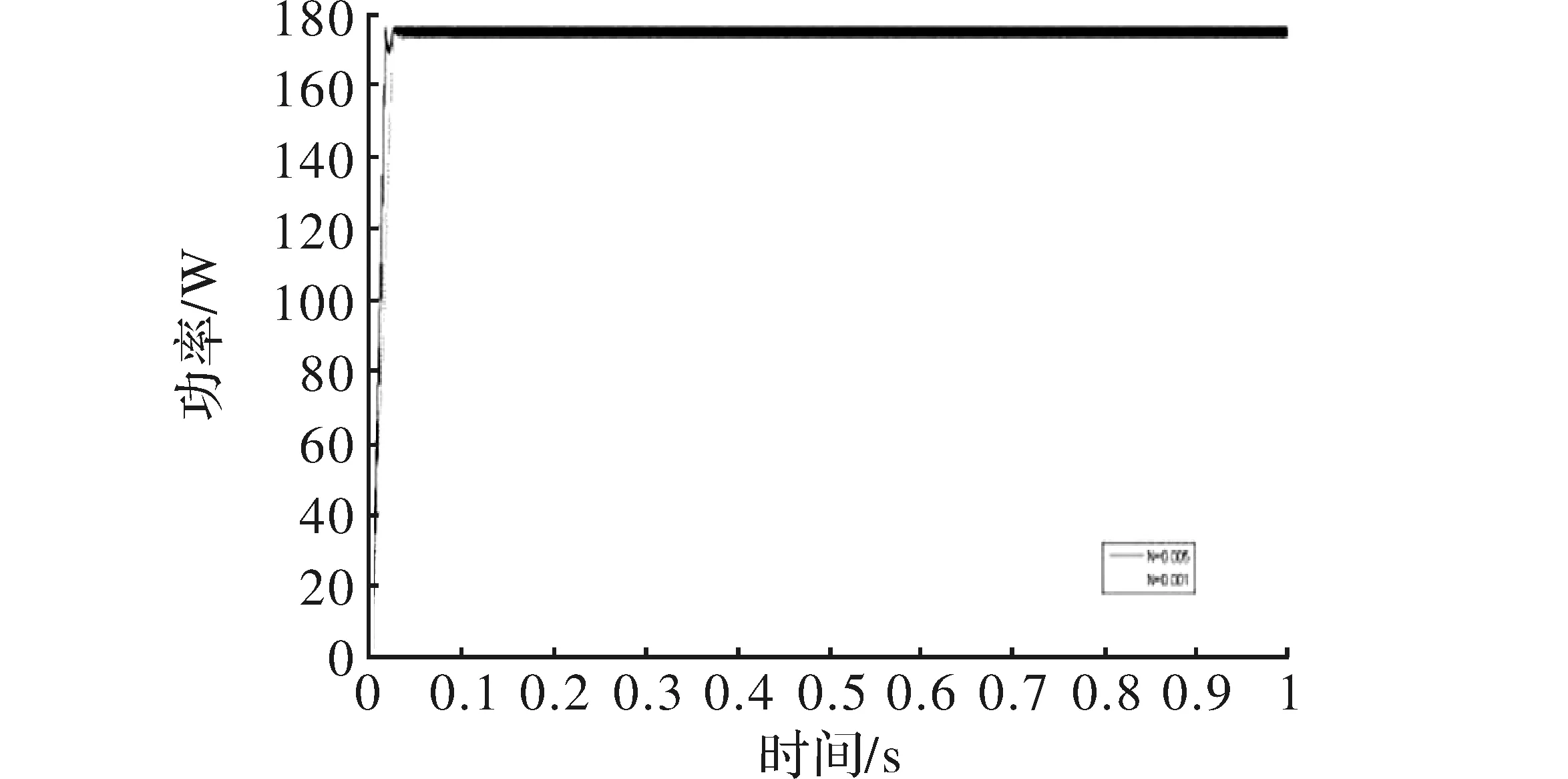
图7 标准状况下光伏电池板输出功率

设置初始工作条件为标准状况下，温度保持不变，t=0.4 s时，外界光强增加为2 000 W/m2；t=0.8 s时，外界光强降低为1 500 W/m2，步长速度因子N分别取0.005和0.001，仿真结果如图8所示。

图8 光照强度变化时光伏电池板输出功率

设置初始工作条件为标准状况下，光强保持不变，t=10.4 s时，将温度升高到T=40 ℃；t=0.8 s时，将温度降低到T=10 ℃，步长速度因子N分别取0.005和0.001，仿真结果如图9所示。

图9 温度变化时光伏电池板输出功率

由图7可知，N取值0.001时，系统快速追踪到了最大功率点，时间约0.04 s。N取值0.005时，由于扰动步长的增加，追踪速度加快，系统达到最大功率点的时间缩短为0.03 s，虽然输出功率波动略有增值在允许波动范围之内。

由图8～图9可知：环境因素突变时，选取较大的N值，可以获得更快的响应速度，光伏电池总是稳定输出当前条件下所能达到的最大功率。

仿真结束后点击Generator可以生成HDL网表、NGC网表等多种网表文件，在其生成网表文件的同时还可以选择生成Testbench文件，用于ISIM、Modelsim等第三方软件的仿真。本设计中选择生成HDL网表，生成结果消耗资源如表1所示。

表1 MPPT模块所需FPGA资源

综合图7～图9及表1分析，改进的扰动观测法硬件实现后，结构更简单、所需FPGA资源更少，在标准条件下或环境突变时，均能快速追踪到最大功率点，并保持稳定的输出功率。当N取值0.005时，达到最大功率点只要0.03 s，这优于文献[8]中0.16 s、文献[7]中0.1 s的MPPT追踪时间，也优于传统定步长扰动观测法0.3 s的MPPT追踪时间[13]。

5 结束语

本文在对传统扰动观测法进行研究与分析的基础上，提出了一种改进的变步长扰动观测法，该算法具有结构简单、MPPT响应速度快、输出稳定的特点，通过使用SG和Simulink标准工具箱对改进的算法进行混合建模仿真，验证了算法的快速性与稳定性。采用SG/Simulink混合建模仿真，相较于传统的VHDL语言设计而言更加简单、直观，使设计者可以将精力集中于算法的功能实现，提高了设计效率，为下一步光伏MPPT算法的FPGA实现提供了新的工具与手段。

[1] 丁明,王伟胜,王秀丽,等.大规模光伏发电对电力系统影响综述[J].中国电机工程学报,2014,34(1):1-14.

[2] 焦阳,宋强,刘文华.基于改进MPPT算法的光伏并网系统控制策略[J].电力自动化设备,2010,30(12):92-96.

[3] 刘邦银,段善旭,刘飞,等.基于改进扰动观察法的光伏阵列最大功率点跟踪[J].电工技术学报,2009,24(6):91-94.

[4] Rasoul Faraji,Amin Rouholamini,Hamid Reza Naji,et al.FPGA-based real time incremental conductance maximum power point tracking controller for photovoltaic systems [J].The Institution of Engineering and Technology,2014,7(5):1294-1304.

[5] 张育宾, 张文生. 基于Matlab下的光伏电池模型及 MPPT研究[J]. 电子科技, 2015, 28(10):179-181.

[6] 孙会明, 陈薇. 基于粒子群优化的光伏MPPT算法 [J]. 电子科技, 2014, 27(6):187-189.

[7] 张建坡,张红艳,马朝晖.光伏系统变步长最大功率跟踪策略仿真研究[J].可再生能源,2009,27(5):10-14.

[8] 杭凤梅,杨伟,朱文艳.光伏系统MPPT的扰动观测法的分析与改进[J].电力系统保护与制,2014,42(9):110-114.

[9] 纪志成，高春能.FPGA数字信号处理设计教程[M].西安:西安电子科技大学出版社,2008.

[10] 纪志成,陈娅冰,周治平.基于SG/Simulink无刷直流电机混合建模与仿真研究[J].系统仿真学报,2005,17(3):525-528.

[11] 万晓凤,张燕飞,余运俊,等.光伏电池工程数学模型的比较研究[J].计算机仿真,2014,31(3):113-117.

[12] 茆美琴,余世杰,苏建徽.带有MPPT功能的光伏阵列Matlab通用仿真模型[J].系统仿真学报报2005,17(5):1248-1251.

[13] 刘栋，杨苹，黄锦成.一种光伏发电系统变步长MPPT控制策略研究[J]. 电气传动,2011,41(4)：35-38.

An Improved MPPT Algorithm Based on SG/Simulink

WANG Haiyan，QIN Jian，WANG Xujia

(School of Automatic Engineering,Shanghai University of Electric Power，Shanghai 200090，China)

Aiming at the problems that tracking speed and precision are not ideal in the traditional MPPT algorithm,the output characteristics of PV cells under different environment were analyzed,and an improved variable step size perturbation method is proposed.The algorithm use the new adaptive step size formal as the disturbance step length.It makes the photovoltaic cells in large steps to quickly approach the maximum power point, and then in a smaller step to stabilize the maximum power point.Finally,the simulations are carried out under the SG / Simulink hybrid modeling and simulation platform. The results show that the algorithm can significantly improve the maximum power point tracking speed and accuracy.

MPPT；disturbance observer method；System Generator(SG)

2016- 11- 16

上海市电站自动化重点实验室资助项目(13ZD2273800)

王海燕(1976-)，女，副教授。研究方向：电站自动化等。秦健(1990-)，男，硕士研究生，研究方向为光伏并网发电控制系统等。

10.16180/j.cnki.issn1007-7820.2017.04.026

TM914.4

A

1007-7820(2017)04-103-04