基于Matlab和Adams的超速机柔性轴系仿真

朱呈祥，沈景凤

(上海理工大学 机械工程学院，上海200093)

基于Matlab和Adams的超速机柔性轴系仿真

朱呈祥，沈景凤

(上海理工大学 机械工程学院，上海200093)

在通用型机械强度超速试验机的柔性系统中，柔性轴在高转速下会出现变形过大的问题，影响试验结果的准确性。结合以往设计经验，在理论研究的基础上，利用有限元法和拉格朗日方程建立柔性轴系运动方程，运用Matlab求解出相应的质量矩阵、刚度矩阵，得出了柔性轴系在瞬态和稳态情况下的运行情况。并利用Adams进行柔体动力学分析，得出在瞬态和稳态情况下柔性轴系的运行情况与理论计算结果进行对比，其结果基本一致，验证了理论计算和系统柔性仿真的正确性。

柔性轴系;newmark-β;Adams;柔性仿真

超速试验机是一种用来检测材料性能及机械结构设计是否合理的机器[1]，超速试验机中的柔性轴系起到通过旋转方式传递能量的作用，在实际试验过程中，当柔性轴振动过大时，极端情况下会出现断裂的情况，对人员安全和试验结果的准确性造成影响[2]。本文在综合考虑超速机柔性轴、弹性支撑的情况下，利用有限元与多体动力学知识建立起系统的动力学模型和动力学方程，并且利用Matlab进行数值求解，利用Adams建立整个系统的柔性体模型并对模型进行仿真，对结果曲线进行对比和分析，验证了推导出的动力学方程。

1 柔性转子系统模型

1.1 模型建立

关于转子系统的研究是在Jeffcott模型的基础上进行，主要研究思路包括考虑轴的质量、惯性和扭转刚度，另外一些研究则集中在转子的支撑上，在以上研究的基础上综合考虑柔性轴的扭转、弯曲和弹性支撑的情况下，研究柔性轴系的动力学响应[3]。

1.2 理论基础

1.2.1 柔性体的拉格朗日方程

质量矩阵组装形式如下

(1)

(2)

(3)

分别求出各段轴单元的刚度矩阵，然后利用Matlab进行组装，得到转轴的总刚度矩阵。总刚度矩阵也是一个17阶对称矩阵，对应的广义坐标

qf=[q3,q2,q1,qc,qb,qa,q6,q5,q4,qf,qe,qd,q9,q8,q7,qi,qh,qg]

因为转轴的质量矩阵是一个时不变矩阵，即不随运动的发生而发生变化，因此转轴的质量矩阵对时间的导数为0[6]

(4)

系统的广义坐标可以表示为

qf=[θ,φ,q3,q2,q1,qc,qb,qa,q6,q5,q4,qf,qe,qd,q9,q8,q7,qi,qh,qg]

综合考虑转子和柔性轴的运动方程，利用拉格朗日方程可以得到柔性转子系统的动力学控制方程[7]

Mq″+Kq=QF+QV

(5)

(6)

式中，M为整体质量矩阵；K为柔性轴的整体刚度矩阵；M′是质量矩阵对时间的求导；QF为外力矩阵。M是由视为刚体的转子质量矩阵(17×17)与柔性轴的质量矩阵 (17×17)组集而来。在建模过程中，将转子划分到柔性轴的第二个节点上，因此这里把转子的质量矩阵叠加到柔性轴的第二个节点上，由此可以得到整个系统总的质量矩阵。

在得到柔性轴系统的总质量矩阵后，代入拉格朗日方程，可得与速度二次项有关的广义力的表达式

(7)

1.2.2 纽马克法

纽马克法是目前解决二阶微分方程常用的一种数值方法，是一种无条件稳定的数值积分方法[8],可以当成是线性积分格式的推广，所用格式为

(8)

(9)

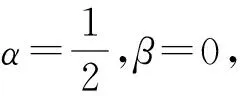
(10)

(11)

Mq″+Cq′+Kq=Qt

(12)

将式(10)和式(11)带入式(12)得

(13)

(14)

(15)

由上式可以解出qt+Δt，在代入式中可求得t+Δt时刻的速度和加速度。

Newmark-β法的计算步骤：

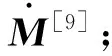
计算有效刚度

K◇=K+a0M+a1M′

(16)

在每一时间步长上，重复进行步骤(4)～步骤(6)；

(4)计算t+Δt时刻的有效载荷

(17)

(5)计算t+Δt时刻的位移

(18)

(6)根据差分格式，计算t+Δt时刻的速度和加速度

(19)

(20)

2 用Matlab求解系统的响应

2.1 瞬态响应

本课题实际模型参数如下：换向器质量2 kg；转轴长度300 mm；转轴直径15 mm；转轴密度ρ=7.8×103kg/m3；剪切模量G=80 Gpa；偏心距e=3×10-5m；驱动转矩τ=1N·m；初始状态的广义坐标(0 0 0 0 0 0 0 0 0.15 0 0 0 0 0.3 0 0)T；两端的阻尼器支撑刚度K=1×107N/M；两端阻尼器的等效阻尼C=1 150 N·s/m。

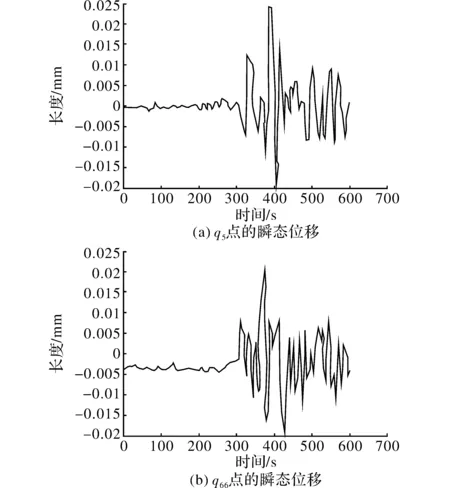
图1 节点1分别在Y轴和X轴方向的响应曲线

由编程求解出的瞬态响应的图像可知，在仿真的前30 s内，曲线运行整体比较平稳。在30～40 s区间内，曲线出现抖动，尤其是在38 s附近区域，曲线的振幅达到峰值，推测此时的振幅有可能是转轴在达到系统一阶临界转速后的共振，这需要在后面的仿真计算中进行验证。随着转速继续提高，在油膜阻尼器和转子自定心的共同作用下，转子的振幅也慢慢降低[12]，与预期相符合。

2.2 稳态响应

换向器质量2 kg；转轴长度300 mm；转轴直径15 mm；转轴密度ρ=7.8×103kg/m3；剪切模量G=80 Gpa；偏心距e=3×10-5m；驱动转矩τ=1 N·m；初始状态的广义坐标(0 0 0 0 0 0 0 0 0.15 0 0 0 0 0.3 0 0)T；两端的阻尼器支撑刚度K=1×107N/M；两端阻尼器的等效阻尼C=1 150 N·s/m；转轴旋转速度45 000 r/min。

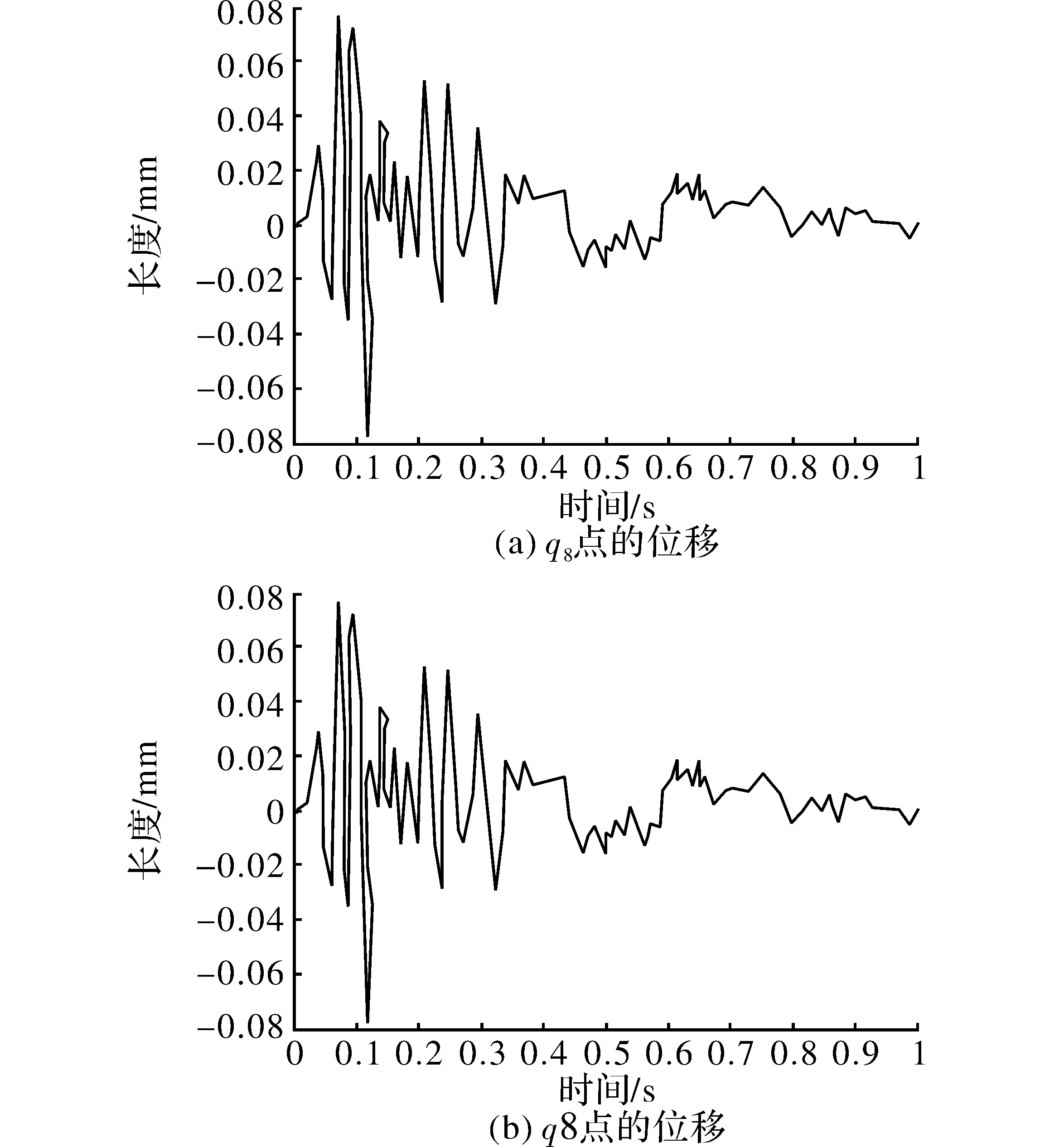
图2 节点2在Y轴和X轴方向的响应曲线

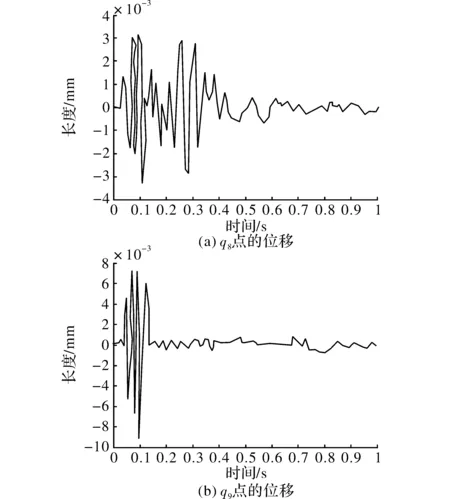
图3 节点3在Y轴和X轴方向的响应曲线

根据模态分析选定稳态响应转速为45 000 r/min 。在这个转速下，程序的求解时间定为1 s，步长为1.0e-6。计算得到的图像如图1～图3所示，不同点的位移响应均不相同，但是都有相似之处。实验开始时，各点的响应曲线都发生震荡。但当迭代计算持续进行时，各点的振幅减小，逐渐趋于稳定。原因是油膜阻尼器的阻尼力有一定的迟滞性，当阻尼力开始减震时，系统振幅逐渐降低，系统的曲线与预期相符合。

3 ADAMS柔性分析及模态响应

3.1 模态响应

实际结构相对简单，直接用Solidworks进行模态分析，分析的步骤如下：(1)给试件附加材料;(2)添加约束;(3)添加外部载荷。系统的前三阶模态列表如表1所示。

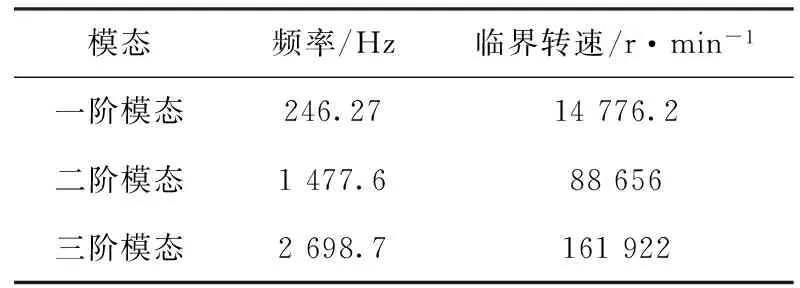
表1 频率转速表

相应转速计算公式为

(21)

其中，D为直径；v为速度。得出n=45 000 r/min在这个速度区间需要通过一阶临界状态。因此为了试验能够顺利进行，需要超速机以较大的加速度通过一阶临界状态。

试验步骤[13]：(1)先将转速匀速加载至约12 500 r/min；(2)以较大的加速度通过一阶临界状态；(3)平稳加载到45 000 r/min，稳定3 min。

模态分析完成后，在Adams中进行动力学仿真。试验轴长度300 mm，卧式布置，轴半径为15 mm。在Adams中因为理论的限制，柔性体和刚性体不能直接接触，尤其是对于在柔性体上施加多分量力和力矩，同时也不能直接在柔性体上施加滑移副约束和平面副约束等。所以将创建的构件质量和惯性矩等质量信息设为0，这样在保留虚构件外观的同时，也能保证在柔性件与刚性件之间发生正确的联系[14]。

根据给定参数建立3D模型，利用Adams/AutoFlex模块的第二种方式建立柔性体[15]，设置仿真参数，进行仿真。

3.2 瞬态响应

在求瞬态响应前，需要用到Adams中的step函数。利用step函数处理,step函数表示为:step(time,0,0,75 000d,100)+step(time,100,0,25 000d,20)+ step(time,120,0,300,900 00d)+

step(time,300,0,420,900 00d)+step(time,420,0,600,0d)，得到瞬态响应图像如图4所示。

图4 节点1分别在Y轴和X轴方向的响应曲线

由瞬态响应的图像可知，在仿真的前25 s内，曲线比较平稳，在约36 s曲线出现了一个较大的振幅，这是柔性转子通过一阶临界转速时共振所引起的。随着转速慢慢远离临界转速，并且在转子自定心的作用下，转子的振幅也逐渐降低，与预期相符合。

3.3 稳态响应

取稳态旋转速度45 000 r/min；仿真时间为1 s；步长1 000。节点2和节点3的稳态位移图像如图5和图6所示

图5 节点2在Y轴和X轴方向的响应曲线

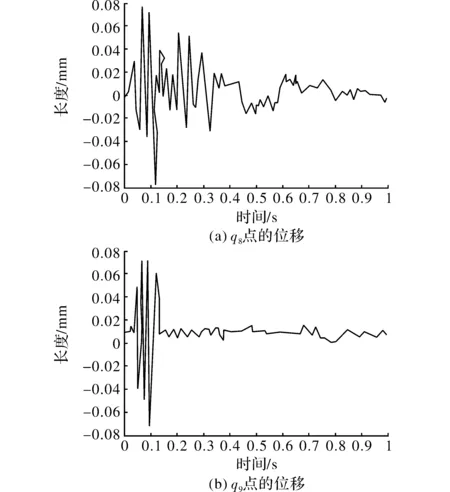
图6 节点3在Y轴和X轴方向的响应曲线

4 结果对比分析

结果进行对比分析：

(1)瞬态响应曲线对比：对比图1(a)和图4(a)可以看出，两者的变化趋势基本一致。在图1(a)中振幅的幅值为0.021 mm，而在图4(a)中，振幅幅值为0.025 mm，振幅差距非常小。对比图1(b)和图4(b)可知，在300 s前，两者的振幅变化幅度都很小，但图4(b)的变化更平稳；在300 s后，即柔性轴的转速达到一定程度时开始发生震荡，随着转速接近阶临界转速，振幅达到最大。最大值分别为0.02 mm和0.024 mm，之后随着转速远离临界转速，振幅逐渐降低；

(2)稳态响应曲线对比：稳态转速45 000 r/min是由换向器的实验要求规定的。对比图2(a)和图3(b)发现二者在开始均剧烈震荡，但后者震荡比前者更剧烈。随后仿真计算得出的图4(a)振动比较有规律，而图2(a)则杂乱无章。原因是在实际仿真时将油膜阻尼器的弹性刚度设为常数，这导致在系统的振幅很有规律。而理论计算是通过迭代求解，其计算结果则没有规律。在随后的几张图像中都出现了类似的问题。对比转子在柔性轴上的图3(a)和图5(a)可知，两者的平衡位置不一致，前者是在0附近震荡。而后者是在2附近震荡。但随后两者的振动趋势一致，都是振幅逐渐减小。这是阻尼器和柔性轴的自定心共同作用的结果。而从图3(b)和图6(b)可知，两者在图像的幅值和变化趋势上均一致。

5 结束语

本文通过利用有限元法和拉格朗日方程计算得到的结果和Adams柔性仿真得出的结果一致，验证了理论计算和系统柔性仿真的正确性。利用有限元与多体动力学建立系统的动力学模型和方程，用Matlab进行数值求解，能够快速得到柔性轴在不同运转状态下和不同位置时的形变量，加快了超速机的研发进程。

[1] 崔陵军,陈欣.通用型机械强度超速试验机[J].电动工具,2010,20(5):11-12.

[2] 陆军毅,吴荣仁.转子失效分析的重要试验-转速超速破坏试验[J].机电工程材料,1992,93(12):1-3.

[3] 顾家柳.转子动力学[M].北京:国防工业出版社,1985.

[4] 林乐新.ZUSTD型倒挂式叶轮超速试验机的设计与开发[D].杭州:浙江大学,2011.

[5] 杨辉,洪嘉振,余征跃.柔性多体系统力学实验研究综述[J].力学进展.2004,34(2):171-181.

[6] 许涛.弹性轴-柔性支撑转子系统动力学研究[D].西安:西安电子科技大学,2010.

[7] 徐美娟.弹性轴-刚性轴转子系统动力学研究[D].西安:西安电子科技大学,2010.

[8] 罗敏,刘巨宝.用Newmark法求解旋转细长梁的影响因素分析[J].大庆石油学院学报,2003,11(1):1-3.

[9] 瞿婉明.大型结构动力分析的Newmark显式算法[J].重庆交通学院学报,1991,10(2):2-4.

[10] 李长青,楼梦麟.中心-偏心差分法[J].同济大学学报:自然科学版,2011,39(11):1-4.

[11] 莫勒.Matlab数值计算[M].喻文健,译.北京:机械工业出版社,2006.

Simulation of Speed Flexible Shaft Machine Based on Matlab and Adams

ZHU Chengxiang，SHEN Jingfeng

(School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

This paper is a speeding enterprise design of general purpose mechanical strength testing machine. The flexible shaft speeds up under the high speed ，deformation is too large and affect the test questions. Using the Lagrange equations, and establishing the whole equation, then using the Matlab programming to solve the corresponding mass matrix, stiffness matrix, and the matrix of different units set. Using the method of center difference method newmark-beta final Lagrange equation for the numerical solution. Then using the Adams to flexible-body dynamics analysis, it is concluded that the running situation of each part of the flexible shaft system correct.

flexible shaft system；newmark-β；Adams；flexible simulation

2016- 05- 10

朱呈祥(1992-)，男，硕士研究生。研究方向：机电产品设计与控制。沈景凤(1968-)，女，博士，硕士生导师。研究方向：机械设计与理论。

10.16180/j.cnki.issn1007-7820.2017.04.025

TH39

A

1007-7820(2017)04-098-05