一种基于遗传算法的轨道交通乘车路径求解方法

白宏图，刘华

(西安铁路职业技术学院，陕西 西安 710014)

一种基于遗传算法的轨道交通乘车路径求解方法

白宏图，刘华

(西安铁路职业技术学院，陕西 西安 710014)

针对城市轨道交通最佳乘车路径问题，改进了一种城市轨道交通网络建模方法，提出了一种基于遗传算法的乘车路径求解方法，方法还可实现对多条乘车路径的优化排序。实例计算表明方法简单实用，合理可行。

城市轨道交通；遗传算法；路径优化；乘车；交通网络；模型

0 引 言

随着我国经济和城市建设的迅速发展，越来越多的城市开始兴建大量的轨道交通，人们已逐步适应这种快速便捷的出行方式。由于城市结构的复杂性和人们出行的随机性，从出发地到目的地可能会有多种选择路径，也经常会面临不同线路之间的换乘，如何快速寻找一条快捷便利的乘车路径，不仅是每个乘客关心的问题，也是不同运营商在车资分配中以及轨道交通的设计时都会面对的问题[1]。

对于城市轨道交通最佳乘车路径问题，由于站点线路的离散特征，一般很难写出问题的解析表达，故传统的优化计算方法很难得以应用，而作为现在优化算法之一的遗传算法对各种复杂系统具有优良的自适应和优化能力，可将其应用与城市轨道交通最佳乘车路径的优化问题,本文在该领域运用了遗传算法，获得了良好的应用效果[2]。

1 问题描述

城市轨道交通最佳乘车路经可描述为：已知乘客的“起始站点”和“目标站点”，求解从“起始站点”到“目标站点”的最佳路径，本文进一步假设最佳路径即为通过的站点最少的路径，忽略不同站点间行车时间的差异和站点换乘所耗费的时间。

必须明确的是，起始站点和目标站点之间是可到达的，实际中城市轨道交通网内一般不会存在一条和其他轨道均不相连通的轨道，若存在，该轨道可另行单独处理，因此，实际要面对的是若干相交的轨道构成的复杂轨道网络。

实际的城市轨道交通网络较为复杂，研究是需要简化处理，城市轨道交通站点可分为两类：(1)各条轨道相交的“换乘站点”；(2)不是“换乘站点”的“其他站点”。实际乘车过程中，只有遇到“换乘站点”，才会遇到选择路径的问题；若乘客位于“其他站点”，一般只会沿着来路继续前进，沿原路返回显然是不符合逻辑尝试的，也是任何优化过程肯定会淘汰的选择，因此对于“其他站点”不存在路径选择的问题。若起始站点和目标站点不是“换乘站点”，则可转化为线路上下游“换乘站点”来处理。本文的处理方法和文献[3]有所差异，更加简化。

图1 上海市轨道交通 网络简化模型

本文同样以文献[3]提供的上海市轨道交通线路为案例对象进行分析，根据本文上述简化，上海市轨道交通线路可简化为图1所示模型。按照本文上述假设，文献[3]中处理站点1到站点6的问题，在本文中即被转化为求解站点2到站点7的问题，两者是完全等效的，但本文的计算量会明显降低。

针对本文问题，建立结构体数组A[M],其中M为总“换乘站点”数，A[i]为第i个“换乘站点”对应的结构体。结构体定义为{int K;int I[K];int J[K]}，其中K为与每个“换乘站点”直接相邻的“换乘站点”的数目，int I[K]依次标记了每个相邻“换乘站点”的编号，而int J[K]则依次表示两个相邻“换乘站点”之间所经过的路段数，即所谓的权值，而非文献[3]中的站点数，这样更能反映路径的距离远近，所以图1和文献[3]中站点间的数字有所差异[3]。

2 方法描述

2.1 遗传算法介绍

遗传算法是一种借鉴生物界自然选择和自然遗传机制的高度并行、随机、自适应搜索算法，它主要用在处理最优化问题和机器学习。隐含并行性和对全局信息的有效利用能力是遗传算法的两个显著特点，使遗传算法只需检测少量的结构就能反映搜索空间的大量区域，并具有鲁棒性。与传统的优化算法相比，遗传算法主要有以下几个不同之处：(1)遗传算法不是直接作用在参变量集上，而是利用参变量集的某种编码；(2)遗传算法不是从单个点，而是从一个点的群体开始搜索；(3)遗传算法利用适应值信息，无须导数或其他辅助信息；(4)遗传算法利用概率转移规则，而非确定性规则。因此遗传算法对于非解析离散问题具有较好的实用性[4]。

2.2 遗传算法的优化设计流程

图2所示为标准遗传算法程序框图，本文遗传算法就是基于此流程开展设计[5-6]。

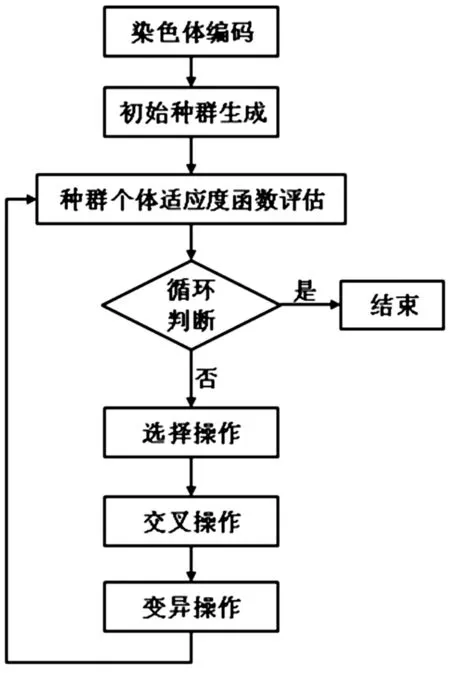
图2 标准遗传算法框图

(1)染色体编码

染色体为规模等于总“换乘站点”数目M的一维整数数组，数组的第一个数值为“起点站点”编号，后续数值对应不同的“换乘站点”编号。前后两个数值编号代表的“换乘站点”必须连接，这条约束可结合对结构体数组A[M]中相应结构体内容int I[K]的随机选取来实现。

一条染色体中不能同时出现两个相同的“换乘站点”，这条约束可通过将简单的循环判断算法加在上一条约束上实现，即通过判断将结构体内容int I[K]中已经在前面出现过的站点排除在随机选取对象之外，这样会出现符合条件的“换乘站点”不存在的情况，此时将下一级“换乘站点”设为“目标站点”，并将这两个站点之间的权值取为轨道交通网络总路段数，后续站点均设为“目标站点”，“目标站点”之间的权值为0。

通过从前到后一级级连续“换乘站点”的生成，直到出现“目标站点”，后续站点均设为“目标站点”，“目标站点”之间的权值为0。

(2)初始种群生成

利用上述染色体编码原理，生成初始种群。由于染色体编码约束较多，生成质量高，多样性好，所以初始种群规模不需要太大，30～50已经足够。

(3)种群个体适应度函数评估

个体适应度函数是反应个体优劣的指标，合理的适应度函数可大大加快最优解的收敛速度，本文个体适应度函数如下：

F(x)=1-f(x)/Gmax

(1)

f(x)为每一条路径上所经过的路段数的总和，即权值的总和，Gmax为轨道交通网络的总路段数，即总权值。本文个体适应度函数值越大，路径经历的总路段数越小，表明个体越优秀。

(4)选择操作

选择操作是依据个体适应度函数，基于优胜劣汰的原则从种群中挑选比较优异的个体遗传至下一代种群中。个体适应函数值越大，个体越优秀，被选中的概率越大。本文实用了最优保全策略，即将最优个体不加改变的直接遗传给下一代，而将权值大于轨道交通网络总权值的个体(即F(x)<0)全部淘汰掉，在下一代中按照染色体编码发生重新生成新的个体。

(5)交叉操作

选择两个未经淘汰的个体，寻找是否存在除“初始站点”和“目标站点”外编号相同的站点，若存在，则从该“换乘站点”开始将后续站点进行交换，若不存在，重新寻找两个个体进行交叉操作。

(6)变异操作

根据一定的变异概率来改变产生新的个体，可以避免遗传算法计算陷入局部最优。本文针对被选中个体进行变异操作时，选中除“初始站点”和“目标站点”外的任一“换乘站点”，从该站点开始，利用染色体编码方式，重新生成后续“换乘站点”。

(7)优化路径求解

按照图2流程，不断循环执行上述操作，经过一定的进化代数，即可获得最优路径。若执行过程中发现最优路径总权值不变而路径不断变化，说明存在多条总权值相同的最优路径，则在下一次执行程序时，将某条最优路径的总权值设置为轨道交通网络的总权值，即将这条路径淘汰掉。通过这样的操作，通过一次次执行程序，不仅可以找到多条最优路径，而且可以对所有可到达的路径进行排序，逐渐找到次优路径，次次优路径。

3 实例计算

初始种群大小取为50，交叉概率取0.5，变异概率取0.1，进化代数取100，站点4到站点10的前4条最优路径如表1所示。

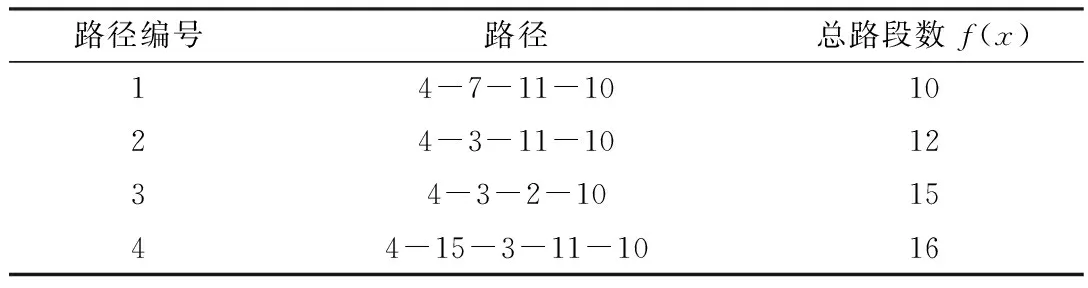
表1 站点4到站点10的前4条最优路径

从表1可以看出，本文所采用的方法和文献[3]获得的路径完全相同，由于采用了路段数而非站点数描述路径长度，所以各条路径的总权值f(x)存在差异，但这并不影响问题的最终求解。

4 结束语

本文改进了一种城市轨道交通网络的简化模型，并提出了一种基于遗传算法的轨道交通乘车最优路径求解方法，实例计算表明该方法不仅可以求解最优乘车路径，还可以对乘车路径进行优化排序，简单实用，合理可行。

[1] 代才. 基于分解的多目标进化算法研究[D]. 西安:西安电子科技大学, 2014.

[2] 谭艳艳. 几种改进的分解类多目标进化算法及其应用[D]. 西安:西安电子科技大学, 2013.

[3] 叶晋,史有群,样学斌,等. 遗传算法在轨道交通换乘路径求解问题上的应用[J]. 电脑与信息技术, 2009,17(4)：24-27.

[4] 董妍汝. 基于选择算子的遗传算法改进[J]. 办公自动化(学术版), 2015,21(16):59-61.

[5] 吴亮红.多目标动态差分进化算法及其应用研究[D]. 湖南大学, 2011.

[6] FAN HY, LU JWZ, XU ZB. An empirical comparison of three novel genetic algorithms [J]. Engineering Computations, 2000,17(8):981-1001.

A Solution for Rail Transit Riding Path Based on the Genetic Algorithm

Bai Hongtu, Liu Hua

(Xi’an Institute of Railway Technology, Xi’an Shaanxi 710014, China)

With regards to optimization of riding path for urban rail transit, this paper presents an improved modeling method for urban rail transit networks, and proposes a rail transit path solution based on the genetic algorithm, which can realize optimal sequencing of multiple riding paths. Practical calculation shows that this method is simple, practical, reasonable and feasible.

urban rail transit; genetic algorithm; path optimization;riding;traffic network;model

10.3969/j.issn.1000-3886.2017.02.012

U212

A

1000-3886(2017)02-0039-02

白宏图(1981-)女，陕西咸阳人，硕士，大学讲师，研究方向：计算机技术、计算机网络。

定稿日期: 2016-08-07