基于MMC的整流系统在不对称桥臂下的环流抑制方法
李赟贵, 杭丽君, 李国杰
(上海交通大学 电子信息与电气工程学院,上海 200240)
基于MMC的整流系统在不对称桥臂下的环流抑制方法
李赟贵, 杭丽君, 李国杰
(上海交通大学 电子信息与电气工程学院,上海 200240)
模块化多电平变换器(MMC)存在内部环流, 在MMC系统上、下桥臂不对称情况下其环流复杂程度增大。基于平均电容电压的控制模型,通过引入低通滤波环节与准比例谐振控制的方法,完成了对MMC系统在不对称桥臂下的环流抑制。最后,在MATLAB/Simulink仿真系统与实际的三相MMC样机平台上,分别对改进前后的控制方案进行实验。通过仿真与实验结果,验证了基于MMC的整流系统在上、下桥臂不对称情况下,环流抑制策略的有效性。
模块化多电平变换器;环流谐波抑制;电容电压均衡;低通滤波器;准比例谐振控制器
0 引 言
通过调整模块化多电平变换器(modular multilevel converter,MMC)内部子模块串联的个数,可以实现功率与电压等级的变化,理论上可以拓展到任意电平输出[1-5]。相较于其他换流器,MMC具有以下优点:①模块化设计,可实现冗余控制,便于容量匹配,适用于不同的功率需求;②输出电平数多,电压谐波含量少;③各子模块不需要同时导通,降低了桥臂电压变化率和电流变化率,从而减轻了开关器件所承受的应力;④存在公共直流母线,更易实现背靠背连接方式[6]。
目前国内外针对MMC的研究主要集中在环流的分析与控制、电容电压均衡等方面。文献[7]介绍了基于上、下桥臂平均电容电压差值进行环流抑制的策略,这种策略需要所有子模块的电容电压信号,所以对信号采集的设计环节要求偏高。文献[8]通过调节上、下桥臂之间的能量差与能量和来调节MMC内部不平衡电压降,以此实现对环流的精确控制。这种策略需要用到精确的桥臂等效阻抗角,在实际的应用中效果相对较差。文献[9]介绍了一种基于改进阶梯波调制的环流抑制控制策略,对MMC三相桥臂中投入的子模块数目采取动态控制,使得每相投入子模块电压之和接近直流电压,从而达到抑制环流的效果,但是其对控制系统的采样频率要求较高。文献[10]介绍了一种平均电容电压控制模型,该模型分为外环和内环,外环对MMC三相桥臂的平均电容电压进行控制,其输出作为内环环流控制的输入。
同时,在实际的MMC系统中,上、下桥臂的电阻、电感很难做到完全一致,其中的误差会使得环流的成分更加复杂,加大控制难度。本文对MMC在不对称桥臂下的数学模型分析,将低通滤波器和准比例谐振控制器用到改进的环流抑制策略中,以实现对MMC的控制;最后通过实验与仿真对比,验证了基于MMC的整流系统在上、下桥臂不对称情况下的环流抑制策略的有效性。
1 MMC基本原理及数学模型
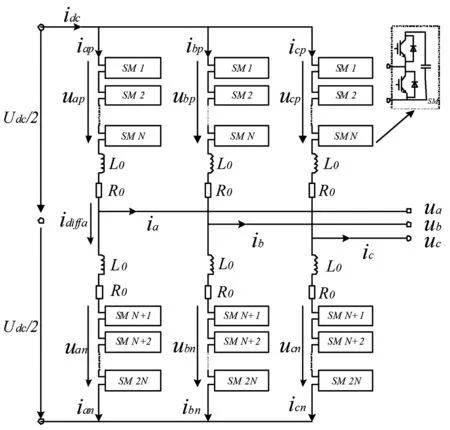
图1 MMC拓扑结构
MMC的拓扑结构如图1所示,每一相都有参数相同且个数相同的子模块(SM)串联而成[11-12];ik为k相输出电流(本文中均有k=a,b,c);ukp和ukn分别为k相上/下桥臂等效输出电压;ikp和ikn分别为k相上/下桥臂电流;idiffk表示同时流经k相上下桥臂的环流。环流和桥臂电流间的关系可以表示如下[13]:
(1)
(2)
即:
(3)
在理想的MMC中,上下桥臂对称,R0为桥臂电感与换流器损耗组成的等效电阻,L0为等效电感;但在实际中,上下桥臂很难完全对称,此时不妨设上/下桥臂等效电阻分别为R1、R2,上/下桥臂等效电感分别为L1、L2。
2 MMC桥臂不对称时的环流分析

图2 MMC单相 电路数学模型
本文采用的独立调制的载波移相调制(CPS-PWM),所有子模块均处于PWM工作状态中。在上、下桥臂不对称的情况下,MMC的单相等效电路图如图2所示。
图2中,单相等效电路上、下桥臂各子模块的电压可以视为交流源ukp和ukn,MMC的输出经负载阻抗后接地。根据基本的电路原理,有:
(4)
(5)
带入MMC数学模型可以推导出:
(6)
一般来讲,由于桥臂电感的滤波作用存在,即使桥臂阻抗不对称,对于负载电流的影响也并不大,可以认为在稳定的条件下桥臂输出的负载电流为标准正弦波形:
ik=Isin(ωt+φ)
(7)
结合上面推导出来的公式(6),其等号右边描述了稳态下环流的频率分量,当L1=L2,R1=R2时(即上下桥臂对称)时,环流主要为直流与二次分量,当L1≠L2,R1≠R2,环流中会引入基波分量。
当对方程(6)进行求解时,其特解部分可以描述环流的稳态特征,其特解方程为:
(8)
其中A1、A2为环流的一次分量、二次分量的幅值系数,其表达式为:
(9)
(10)
可以看出,当上、下桥臂不平衡时,环流的复杂程度极大增加,其环流中主要成分包括直流量、一次分量、二次分量。 对比一次分量与二次分量幅值系数有A2>A1,环流主要的谐波分量为二次分量。
3 针对环流抑制的MMC控制策略
3.1 传统的MMC控制方案
在 CPS-PWM的调制方式下,传统的平均电容电压控制方式如图3所示[14]。上述控制器的主要作用在于平衡桥臂之间的电压。

图3 平均电容电压控制框图
对于上、下桥臂不平衡的MMC系统来讲,其环流的复杂程度较大,其成分除了直流量外,还含有一次、二次分量的谐波。
(11)
式中φ1、φ2为环流一次、二次分量的初始相位角。
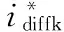
3.2 改进的MMC控制方案
改进的MMC控制框图如图4所示。
图4 改进的环流抑制控制模型
对于一阶低通滤波器来讲,其传递函数为:
(12)
Ts为时间常数,截止频率为1/(2π*Ts)
对于准比例谐振控制器来讲,其传递函数为:
(13)式中Kp、Kr分别为谐振控制器比例项系数及谐振增益;ωc为响应带宽,nω0为n次谐波的频率,本文主要针对一次、二次谐波进行抑制,即n=1,2。为了更好地使低通滤波器提取直流分量,其截止频率取20 Hz,所以有1/(2π*Ts)=20 ,Ts=0.007 9(s)。

4 实验验证
为了验证改进的控制策略对于上、下桥臂不对称的MMC整流器的控制效果,本文首先在MATLAB/Simulink的仿真平台搭建了三相MMC整流系统,对环流抑制策略进行验证。再搭建三相MMC实验样机,运行在整流模式,对环流抑制策略进行进一步实验验证。实验中上、下桥臂电感、电阻取值为0.9L1=L2=3 mH,0.5R1=R2=0.05 Ω。
其他主要的系统参数如表1所示。

表1 系统参数
4.1 SIMULINK/MATLAB仿真实验
本实验MMC系统控制在整流状态,从图5可以看出交流侧三相电压ua,b,c与三相电流ia,b,c处于反相状态,符合实际整流工况。
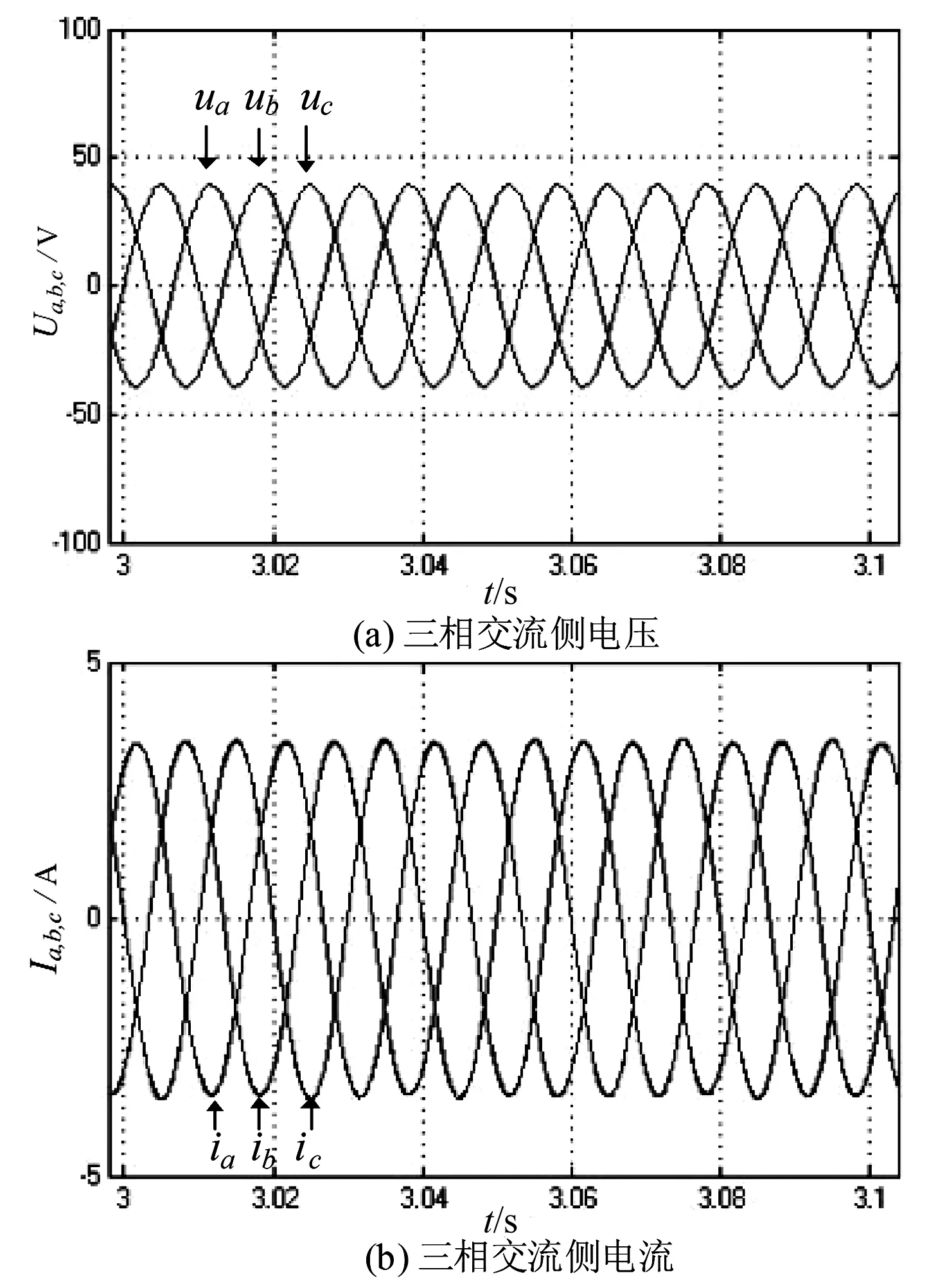
图5 交流侧电压、电流波形
图6、图7为仿真实验中采用传统、改进控制策略的实验波形,其中Udc为整流系统直流侧电压,iap、ian为a相上、下桥臂电流,idiffa为桥臂环流。图中可见采用传统型、改进型的控制策略均对直流侧电压实现了较好的控制。

图7 改进控制策略下仿真波形
对比图6(c)、图7(c)可以看出在传统的MMC控制策略下,环流idiffa的振动幅度大约为0.54 A,而在改进的MMC控制策略下,环流idiffa的振动幅度大约在0.15 A,对环流的抑制效果有了显著的改善,仿真结果验证了改进型MMC控制策略对于环流的控制效果。
4.2 三相样机实验
为验证本文所提出的控制模型的有效性,搭建了三相MMC实验样机。样机控制单元采用TI公司支持浮点运算的DSP控制器以及Altera公司的FPGA控制器。
图8、图9为三相样机实验中采用传统、改进控制策略得到的实验波形,同样以a相为例,对比图8(b)、图9(b),传统的MMC控制策略下环流idiffa的振动幅度大约为0.52 A,而在改进的MMC控制策略下,环流idiffa的振动幅度大约在0.23 A,对环流的抑制效果有了显著的提高。实验结果同样验证了改进型MMC控制策略的有效性。

图8 传统控制策略下的实验波形

图9 改进控制策略下的实验波形
从仿真结果与三相样机实验结果均可看出,使用改进的环流抑制策略后,环流得到了明显的抑制,实验结果与仿真结果相吻合,验证了环流抑制策略的合理性。
5 结束语
本文介绍了MMC的基本数学模型,分析了MMC在桥臂不对称情况下的环流特点,提出针对性的环流抑制策略,通过引入低通滤波环节与准比例谐振控制的方法,完成了对MMC系统在不对称桥臂下的环流抑制。通过在MATLAB/SIMULINK仿真系统与实际的三相MMC样机平台上的实验,对改进前后的控制方案进行对比。通过对仿真与实验结果的分析,验证了在基于MMC的整流系统在上、下桥臂不对称情况下,环流抑制策略的有效性。
[1] 徐政,陈海荣.电压源换流器型直流输电技术综述[J].高电压技术,2007,33 (1):1-10.
[2] FLOURENTZOU N, AGELIDIS V G, DEMETRIADES,et al.VSC based hVDC power transmission systems:An overview[J].IEEE Transactions on Power Electronics,2009,24(3):592-602.
[3] MARQUARDT R,LESNICAR A.New concept for high voltage modulation multilevel converter[C]. Proceedings of the 34th IEEE Annual Power Electronics Specialists Conference.Aachen,Germany:IEEE,2003: 20-25.
[4] LESNICAR A.MARQUARDT R.An innovative modular multilevel converter topology suitable for a wide power range[C].Power Tech Conference Proceedings,IEEE Bologna,20031-6.
[5] 汤广福,贺之渊,庞辉.柔性直流输电工程技术研究、应用及发展[J].电力系统自动化,2013, 37(15):1-14.
[6] AKAGI H. Classification, terminology, and application of the modular multilevel cascade converter (MMCC)[J]. IEEE Transactions on Power Electronics, 2010, 26(11):508-515.
[7] HAGIWARA M, MAEDA R, AKAGI H. Control and analysis of the modular multilevel cascade converter based on double-star chopper-cells (MMCC-DSCC)[J]. IEEE Transactions on Power Electronics, 2011, 26(6):1649-1658.
[8] TU Q,XU A,XU L.Reduced switching-frequency modulation and circulating current suppression for modular multilevel converters[J].IEEE Transactions on Power Delivery,2011,26(3):2009-2016.
[9] 宋平岗, 李云丰, 王立娜,等. 基于改进阶梯波调制的模块化多电平换流器环流抑制策略[J]. 电网技术, 2013, 37(4):1012-1018.
[10] ANTONOPOULOS A, ANGQUIST LENNART NEE. H.P.On dynamics and voltage control of the modular multilevel converter[C].European Conference on Power Electronics and Applications,2009:1-10.
[11] 刘栋, 汤广福, 贺之渊,等. 模块化多电平柔性直流输电数字-模拟混合实时仿真技术[J]. 电力自动化设备, 2013, 33(2):68-73.
[12] 何大清, 蔡旭. 模块化多电平变流器的限幅控制和混合调制[J]. 电力自动化设备, 2012, 32(4):63-66.
[13] HAGIWARA M, AKAGI H.Control and experiment of pulse width-modulated modular multilevel converters[J].IEEE Transactions on Power Electronics, 2009,24(7):1737-1746.
[14] 陆翌,王朝亮,彭茂兰,等.一种模块化多电平换流器的子模块优化均压方法[J].电力系统自动化,2014,38(3):52-58.
A Circulating Current Suppression Method for MMC-based Rectification System with Asymmetric Bridge Arms
Li Yungui, Hang Lijun, Li Guojie
(College of Electronic Information and Electrical Engineering, Shanghai Jiao tong University, Shanghai 200240, China)
There exists circulating current within the modular multi-level converters (MMC). In case the MMC has asymmetric upper and lower bridge arms, complexity of the circulating current will increase. Based on a control model of average capacitor voltage, suppression of circulating current is effected for the MMC system with asymmetric bridge arms through introduction of a low-pass filter and quasi-PR control. Finally, control schemes before and after improvement are tested respectively on MATLAB/Simulink simulation system and a three-phase prototype platform. Simulation and experimental results verify the effectiveness of the proposed circulating current suppression strategy for the MMC-based rectification system with asymmetric upper and lower bridge arms.
modular multilevel converter (MMC); circulating harmonic suppression; capacitor voltage balance; low-pass filter; quasi-PR controller
本论文由国家重点研发计划项目“大型光伏电站直流升压汇集接入关键技术及设备研制”(2016YFB0900200)资助
10.3969/j.issn.1000-3886.2017.02.004
TN624
A
1000-3886(2017)02-0012-04
李赟贵(1991-),男,四川自贡人,硕士生,主要研究方向为电力电子与电力传动。 杭丽君(1979-),女,浙江杭州人,副教授,研究方向为电力电子与电力拖动。 李国杰(1965-),浙江瑞安人,男,教授,研究方向为新能源、电力系统、微电网、柔性直流输电的分析与控制。
定稿日期: 2016-11-21

