预应力折线形铰接钢拱加固拱桥技术试验研究*
彭 凯,乔奋义,贾小飞
(1.重庆交通大学 土木工程学院,重庆 400074;2.广东省南粤交通投资建设有限公司,广东 广州 510101;3.深圳市市政设计研究院有限公司,广东 深圳 518029)
预应力折线形铰接钢拱加固拱桥技术试验研究*
彭 凯1,乔奋义2,贾小飞3
(1.重庆交通大学 土木工程学院,重庆 400074;2.广东省南粤交通投资建设有限公司,广东 广州 510101;3.深圳市市政设计研究院有限公司,广东 深圳 518029)
以新疆某旧拱桥为工程背景,建立其主拱圈缩尺模型,对比分析了缩尺模型在模拟自重荷载作用下,采用预应力折线形铰接钢拱加固前后主要控制截面的应变、挠度及拱圈弯曲能等指标的变化。缩尺模型经加固后,拱圈控制截面的应力水平总体比加固前明显减小;加固对拱轴线形可起到明显的调整作用,且加固后拱圈弯曲能量减少了81%。实验结果表明,预应力折线形铰接钢拱能够有效分担和改善拱肋的自重内力,从而显著提高其抗压承载力。该加固技术对改善类似拱轴线形不佳或自重内力条件不利的上承式拱桥的承载力和使用性能效果显著,可作为拱桥加固的备选技术方案。
桥梁工程;拱桥加固;预应力折线形铰接钢拱;内力优化;拱轴线调整;弯曲能量
0 引 言
拱桥是我国的传统桥型之一。随着交通事业的发展和科学技术的进步,各种新桥型不断出现,但是拱桥仍旧发挥着重大作用。交通量的逐年增加对较早时期建设的在役拱桥提出了更高的承载力和使用性能要求。因此,对大量旧拱桥的加固和技术改造迫在眉睫。目前拱桥的加固方法较多,主要有增大拱圈截面,增强拱肋、拱波之间的联系,加强横向联系,减轻拱上建筑重量等几种基本方法及其组合方法。
预应力折线形铰接钢拱(prestressing hinged piecewise steel arch, PHPSA)加固拱桥是针对拱桥受力特点提出的一种有效的预应力主动加固方法,该方法前期已获得国家发明专利[1]。该加固技术是在上承式混凝土拱桥原主拱圈下增设铰接折线形钢拱圈与原拱腹在折点接触受力,并通过在铰接钢拱拱脚部位设置千斤顶对钢拱圈,进而对原主拱圈施加预应力,达到主动分担原主拱圈在结构自重下的内力,改善优化原主拱圈各控制截面(如拱顶,3L/8,L/4,L/8及拱脚截面等)内力状态(主要是弯矩及偏心距)的目的。PHPSA技术通过预应力调整、优化实现拱桥主拱圈在恒载作用下的内力重分布,有利于削减主拱圈弯矩峰值,降低主拱圈弯曲能量,最后达到提高活载作用下拱桥承载和使用性能的目的。
1 PHPSA加固技术简介[1]
1.1 PHPSA加固结构组成
PHPSA加固是采用钢压杆通过钢铰座两两铰接形成折线形钢拱圈,并在折点钢铰座处与拱桥主拱圈底面相接触而协同受力,再在拱脚部位压杆采用千斤顶施加压力,以此来对钢拱圈及主拱圈施加预应力,调整优化恒载作用下主拱圈内力状态和受力条件的一种高效、经济的拱桥加固新技术。如图1,其加固结构及工艺如下:预应力折线形铰接钢拱(1)由钢压杆(2)、钢铰座(3)、锚固钢垫(4)、拱底黏贴钢板(5)组成,钢压杆(2)之间通过钢铰座(3)铰接,钢铰座(3)法向光滑接触支撑在拱底黏贴钢板(5)上,两侧拱脚钢压杆(2)通过锚固钢垫(4)支承在拱座上。预应力的施加方法采用在两侧拱脚钢压杆(2)下端面和拱座之间安放千斤顶并沿拱脚钢压杆(2)轴心线方向施加设计大小的预顶力,预顶力施加完成以后,采用锚固钢垫(4)填塞两侧拱脚钢压杆(2)下端面和拱座之间的空间,以保存预应力。
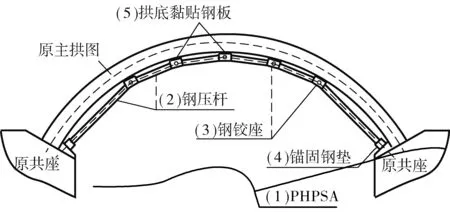
图1 PHPSA加固结构组成Fig. 1 The composition of PHPSA structure
该技术具有显著的技术价值和工程应用价值,其优势如下:
1)折线形铰接钢拱的构件形式简单、轻便,加工、运输及安装快捷,且仅需在两侧拱脚进行预应力施加操作,施工过程对拱桥桥面交通运行无干扰,对原主拱圈结构无损伤。
2)折线形铰接钢拱在施加预应力时通过铰座与原主拱圈底面黏贴钢板的光滑接触形成静定结构,其预应力力学模型简洁,各接触点预加力大小、方向明确,且折线分段数量(接触点数量)和铰节点位置(接触点位置)可根据需要灵活调整,能很好地适应主拱圈不同截面内力调整的特定需求。
3)PHPSA加固法可在不增加原结构荷载的前提下有效改善原主拱圈的恒载内力分布。
4)PHPSA加固法的组成构件在使用期间是可检测、可调整、可维修、可控制和可更换的,为拱桥在使用期的维护管理提供了技术便利,可有效提高拱桥的耐久性,延长拱桥使用寿命。
1.2 PHPSA加固设计原理要点
拱桥在成桥恒载作用下,由于拱轴线与压力线的偏离,主拱圈拱顶、拱脚等截面弯矩值可能偏大,不利于发挥拱圈截面材料的抗压性能优势,削弱了截面承担后续活载效应的富余能力。这一点在一些拱轴线形较差、恒载布置不当、温度及收缩徐变效应考虑不周及施工线形控制不好的拱桥上显得尤为突出[2-9]。因此应控制主拱截面出现恒载弯矩峰值及恒载下拱圈弯曲能量,以达到充分发挥截面材料抗压性能优秀的目的。为此,以成桥恒载作用下主拱恒载弯矩分布为PHPSA加固设计的调整优化对象,分析对拱桥主拱圈增设PHPSA加固处治后的有效性,以此引导加固设计,其要点如下:
1)建立拱桥有限元模型,求得主拱圈弯矩影响线,计算主拱圈各控制截面在最不利恒载组合作用下的内力和变形效应。
2)结合主拱圈最不利恒载弯矩分布及主拱跨径、矢高等拟定PHPSA钢铰座铰节点数量,一般取3,5,7个。跨径较大,矢跨比较小的拱桥铰节点数量可适当增加。这是由于矢跨比较小,则拱圈较坦,铰节点数量少则钢拱圈与原拱圈接触点相对较少,对改善受力较为不利。相对而言矢跨比较大,铰节点可适当减少。
3)在确定了铰节点数量后,铰节点位置的拟定要结合弯矩影响线和主拱圈最不利恒载弯矩峰值位置来进行,一般应布置在结构恒载作用下主拱圈的正弯矩区域。可先假定几种铰节点位置方案,再按后述方法进行铰节点预压力的影响线加载及方案优劣判别。
4)根据拟定的PHPSA铰节点数量和位置,计算拱脚预加力的大小、所需的支撑压杆截面尺寸以及预加力作用效果——加固后拱桥主拱圈弯曲能的大小,并以下式表达的加固效能系数作为判别标准用于加固技术方案的比选:
(1)
式中:κ为加固效能系数,m;U为PHPSA拱脚设计预加力及原结构恒载共同作用下拱桥主拱圈的弯曲能,(kN · m);f为PHPSA拱脚设计预加力,kN。
一般而言,根据式(1)得到的PHPSA加固方案κ值越小,则方案技术经济性能越佳。
2 试验模型简介[9]
2.1 模型拱的制作
为模拟预应力折线形铰接钢拱加固拱桥的技术效果,选取新疆某旧双曲拱桥为原型,该桥为净跨度32.6 m+32.6 m的两跨混凝土双曲拱桥,主拱圈线形为近似圆曲线,中墩为刚性推力墩。主拱圈横向由5道拱肋、4道拱波及上覆拱板组成。根据相似原理,考虑制作方便性及实验室条件,取原型:模型缩尺比为11∶1,并将原主拱圈拱肋较为复杂的截面形式按截面积和截面抗弯惯性矩相似关系,缩小简化为矩形截面[10]。因原桥主拱圈拱脚护拱部分在温度次内力作用下已开裂,其结构效应难以保证,本次试验未模拟护拱作用,以裸拱圈作为主体受力结构进行模拟。
缩尺模型跨径3 m,矢高1.375 m,拱圈采用C40混凝土制作,根据缩尺比配有构造钢筋,截面尺寸宽×高为13.5 mm×15.5 mm;拱圈底面与PHPSA钢铰座接触区域采用环氧树脂胶黏剂黏贴5 mm厚钢板。PHPSA钢压杆采用Q235矩形钢管,其规格为60 mm×40 mm×3 mm;钢铰座采用5 mm厚钢板焊接加工而成,铰座安装位置设置在拱圈的L/4,3L/8,L/2,5L/8和3L/4这5个控制截面处,钢铰座与拱圈底面黏贴钢板接触面上涂有黄油以减小摩擦因数,涂油后界面摩擦因数可取0.05~0.10。采用扁千斤顶在PHPSA拱脚施加轴向预加力。模型拱圈及PHPSA加固布置如图2。
试验分两种工况进行:
Ⅰ. 恒载工况:将原拱桥结构恒载按缩尺比简化为拱上横墙位置的集中荷载,分9个加载点逐级加载于模型拱圈上,测试拱圈恒载效应。
Ⅱ. PHPSA加固工况:维持工况I的恒载状态,在模型拱圈拱腹下方安装PHPSA并分级施加设计预加力,测试PHPSA及模型拱圈的复合受载效应。
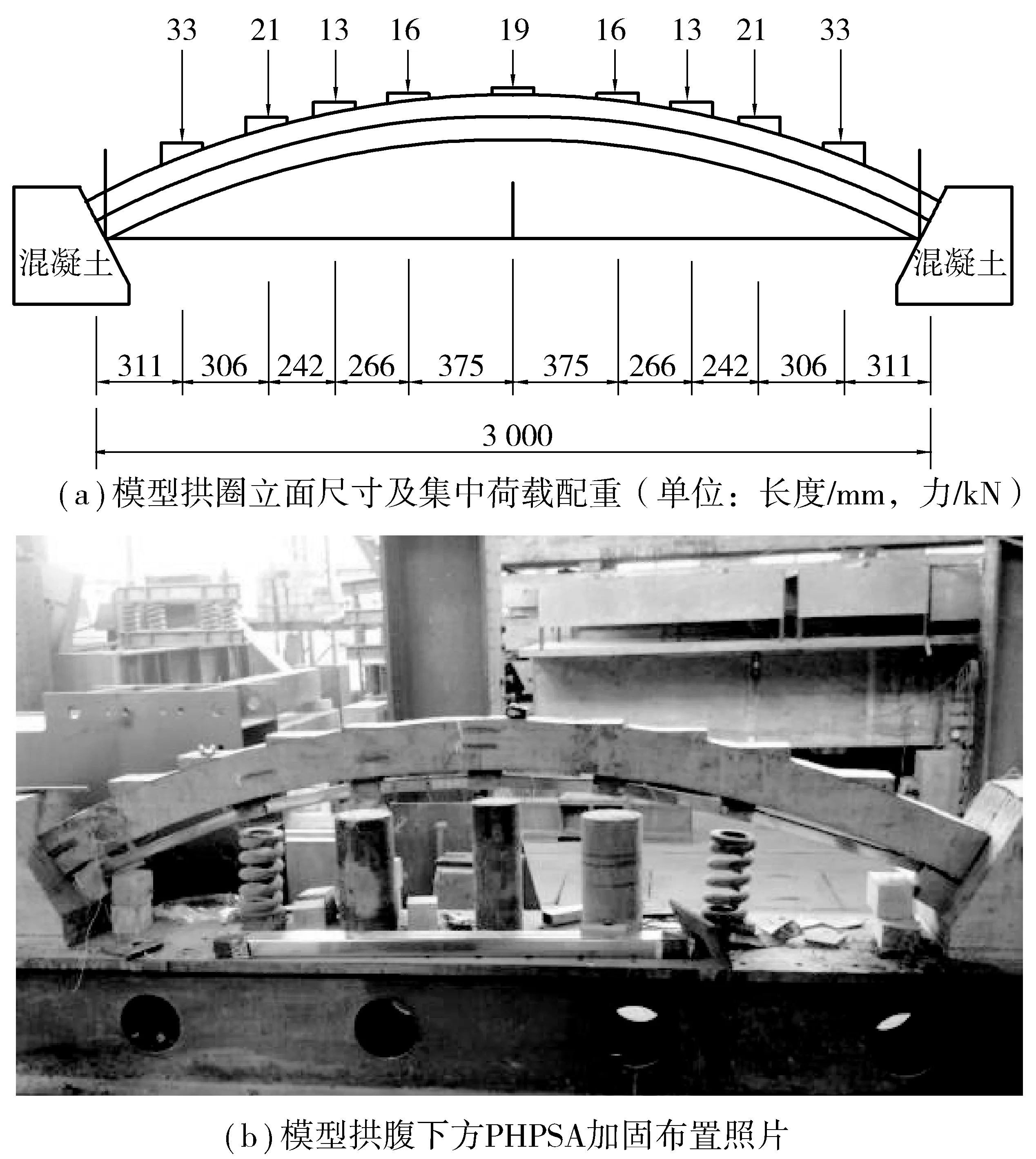
图2 模型拱及PHPSA加固布置立面Fig. 2 The profiles of the model arch and PHPSA
2.2 测点布置与加载方式
2.2.1 测点布置
1)为测试加固前后模型拱的应力、挠度等指标,分别在模型的拱脚,L/4,3L/8,L/2共7个截面布置法向应变片;同时,在模型拱的L/4,L/2布置百分表挠度测点。拱圈测点布置如图3。
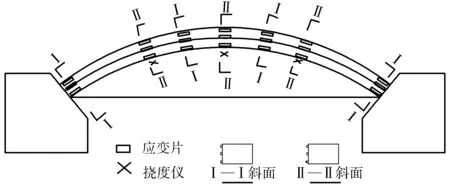
图3 模型拱圈测点布置Fig. 3 The layout of gauging points on the model arch
2)为考察PHPSA钢压杆的受力状态,在各压杆中截面布置了纵轴向应变片。
2.2.2 加载系统
因模型拱尺寸较小,模拟原结构恒载的集中力配重难以直接施加,因此,利用杠杆原理法对模型拱进行配重,以模拟实桥恒载状态,配重加载系统如图4。
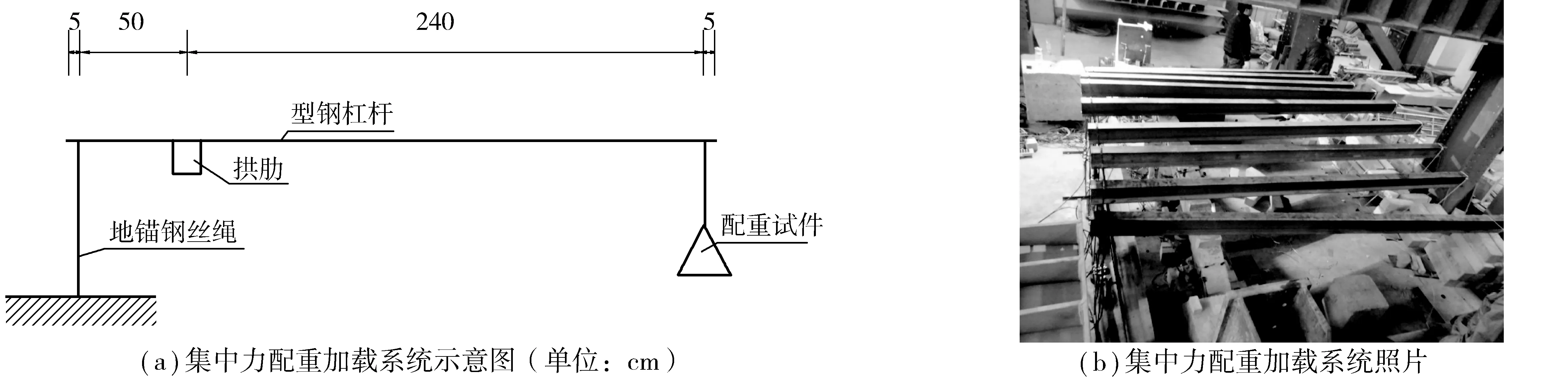
图4 模型拱圈集中力配重加载系统Fig. 4 The concentrated self weight loading system on the model arch
3 试验结果分析
3.1 模型拱圈截面上缘应力变化
在Ⅰ工况下加载至设计值,观测模型拱圈测试截面上缘应力值(拉正压负),然后在持载条件下通过PHPSA拱脚千斤顶施加预加力进入Ⅱ工况,观测各测试截面上缘应力值随拱脚预加力的变化,结果如图5。
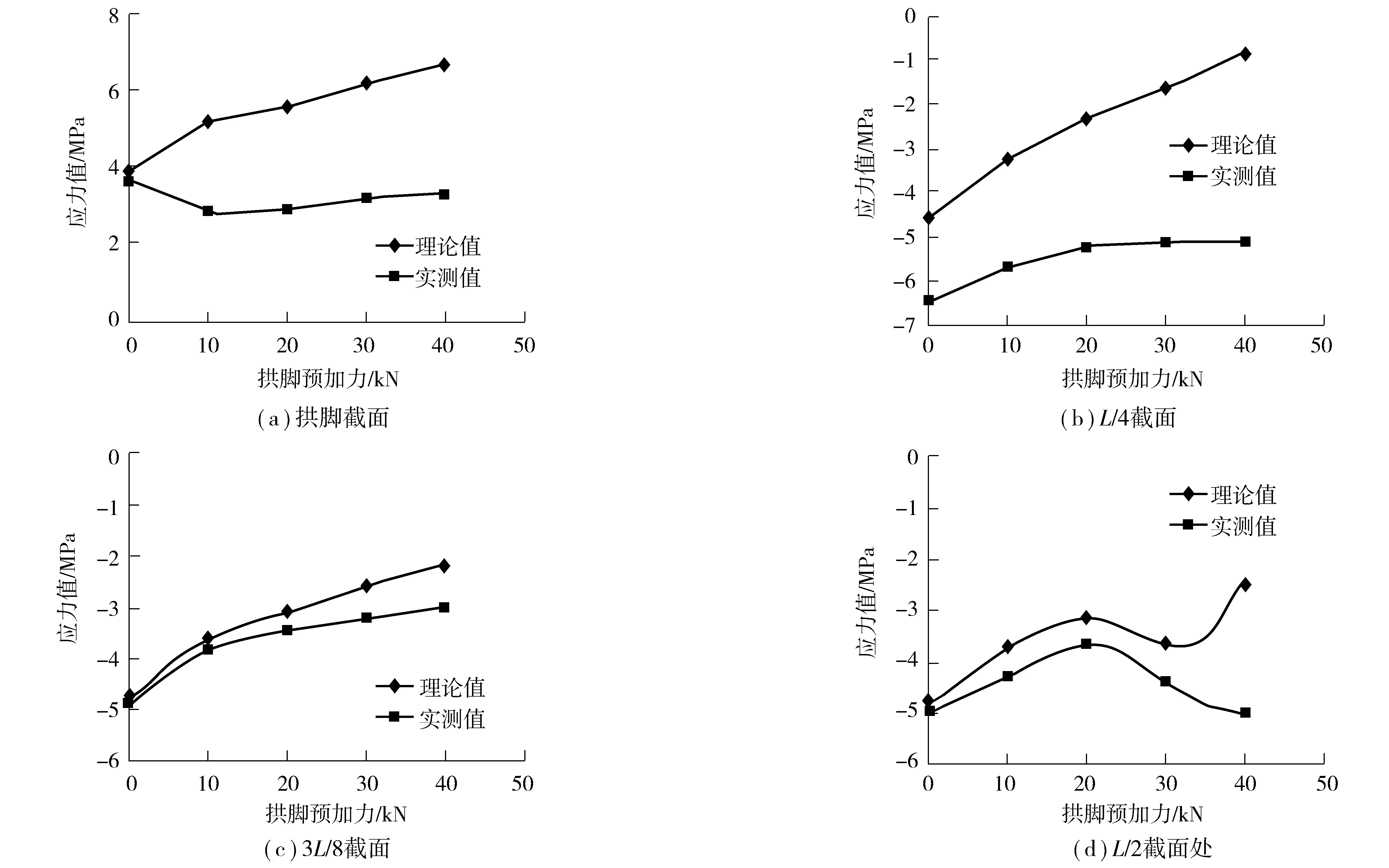
图5 模型拱圈测试截面上缘应力随PHPSA拱脚预加力的变化Fig. 5 Variation of the upper edge normal stresses on the observed cross-sections of the model arch with the prstressing force at the PHPSA foot
由图5所示实测值及理论值结果分析得出:
1)在Ⅰ工况加载到恒载配重设计值后,模型拱圈的拱脚截面上缘存在拉应力值,其余L/4,3L/8,L/2截面上缘存在压应力值。进入Ⅱ工况后,随着PHPSA拱脚预加力的增加,L/4,3L/8截面上缘压应力呈明显下降趋势,证明此PHPSA加固方案对这两个截面起到了明显的内力调整效果。
2)进入Ⅱ工况后,随着PHPSA拱脚预加力的增加,模型拱圈拱脚、L/2截面上缘压应力变化趋势不明显,这是因为:① 模型拱圈拱脚截面附近没有布置PHPSA钢铰座,PHPSA拱脚预加力难以直接对模型拱圈拱脚产生内力调整效应;② 模型拱圈矢跨比较小,属于坦拱,拱顶钢铰座位置预加力传递长度最长、摩擦损失最大且竖向分力较小,预加力对拱顶的作用效应不明显。
3)3L/8,L/2截面上理论和实测值变化趋势吻合较好,而拱脚、L/4截面理论和实测值偏离较大。后经检查分析,在PHPSA拱脚施加预加力时,由于千斤顶出力与PHPSA拱脚压杆轴线对中困难,因此千斤顶的稳定借助了千斤顶与拱脚处加设的垫块,此垫块在千斤顶出力时也会对拱脚有传力作用,但其大小和方向不明,难以理论分析模拟,因此造成拱脚及附近L/4截面理论和实测值偏离较大。这一偏差应在下一步研究中予以修正改进。
4)模型拱圈在Ⅰ,Ⅱ工况下均处于完好弹性状态,而图5所示理论分析和实测应力变化趋势均为曲线,这是因为PHPSA钢铰座与模型拱圈底面黏贴钢板之间为滑动摩擦接触,引入了接触非线性,在有限元数值分析中也考虑了这一实际接触条件,导致理论分析和实测应力变化趋势均为曲线。
3.2 模型拱圈挠度变化
在Ⅰ工况下加载至设计值,观测模型拱圈测试截面挠度值,然后在持载条件下通过PHPSA拱脚千斤顶施加预加力进入Ⅱ工况,观测各测试截面上挠度值随拱脚预加力的变化,结果如图6。

图6 模型拱圈测试截面挠度随PHPSA拱脚预加力的变化Fig. 6 Variation of the deflections at the observed cross-sections of the model arch changing with the prstressing force at the PHPSA foot
由图6所示实测值及理论值结果分析得出:
1)经PHPSA预加力作用后模型拱圈测试截面挠度值明显小于作用前的挠度值,PHPSA拱脚预加力为20 kN时,实测相应挠度值减少达20%~39%,证明PHPSA对调整成桥拱轴线形具有明显效果。
2)模型拱圈测试截面挠度的理论与实测值变化趋势平行,但数值有较明显偏离,经分析主要与前述3.1节所列的PHPSA拱脚千斤顶与模型拱圈拱脚段通过垫块传力不明、钢铰座与模型拱圈底面黏贴钢板摩擦性能难以准确模拟等因素有关。
3.3 模型拱圈弯曲能量分析
拱圈截面如处在理想的轴心受压状态,可以充分发挥截面材料的抗压性能,其承载能力很高。而一旦实际荷载压力线偏离了拱轴线,拱圈截面出现了偏心弯矩及响应的压力线偏心距,其抗压承载力将随着偏心距增大而迅速降低。因此,如何降低拱圈在成桥恒载下控制截面的不利弯矩,成为拱桥设计、施工和加固维护的共同难题[12]。为科学评估PHPSA加固方案对拱桥主拱圈不利弯矩分布的总体调整效果,需计算主拱圈弯曲能在加固前后的变化。常见弹性杆件弯曲能的表达式为:
(2)式中:U为杆件弯曲能,(kN · m);M为杆件截面弯矩,(kN · m);x为杆件长度方向坐标,m;E为杆件材料弹性模量,(kN/m2);I为杆件截面抗弯惯性矩,m4。
采用Midas结构分析软件建立模型拱圈有限元模型,分别求得模型拱圈在PHPSA加固前后的弯矩分布,再利用式(2),分别计算模型拱圈在加固前后的总弯曲能,再根据模型与原型的弯曲能相似比例系数1∶11[3],得到加固前原桥拱圈在结构恒载下的总弯曲能为24.573 kN · m,加固(对应模型的PHPSA拱脚预加力为20 kN)后模型拱圈在结构恒载及预加力共同作用下的总弯曲能为4.695 kN · m,后者相比前者减少百分比为:
由此可见,PHPSA加固技术可以大幅降低拱桥主拱圈弯曲能,从而有效改善主拱圈不利弯矩分布,更加充分地利用截面材料的抗压能力。
按照前述式(1)计算本试验中PHPSA加固方案的效能系数,可得效能系数κ=1.76E-04 m。由于经费和实验条件限制,本次试验未能进行更多PHPSA加固设计方案的对比,这有待下一步研究工作的开展。
4 结 论
笔者就PHPSA加固技术开展新疆某旧拱桥的缩尺模型试验研究,主要研究结论如下:
1)从加固前后模型拱圈截面的应变对比分析可以看出,PHPSA可有效分担拱桥结构的恒载效应,改善主拱圈在结构恒载作用下的应力状态。
2)加固后模型拱圈控制截面在结构恒载作用下的挠度明显减小,说明PHPSA可有效修正拱圈的轴线线形。
3)加固后模型拱圈弯曲能量显著降低,说明PHPSA对改善和优化拱圈在结构恒载作用下的弯矩分布起到了明显作用。
PHPSA用于拱桥加固。在活载作用下PHPSA与原桥主拱圈共同受力,分担活载效应的性能。PHPSA加固技术的预应力损失计算,以及PHPSA钢铰座与原桥主拱圈底面黏贴钢板滑动摩擦接触的模拟等,都还有待下一步深入研究。
[1] 彭凯,程浩,魏文财,等. 拱桥加固型组合拱圈:201110241656.9[P]. 2014-07-02.
PENG Kai, CHENG Hao, WEI Wencai, et al.CombinedArchRingforStrengtheningofArchBridges:201110241656.9[P]. 2014-07-02.
[2] 林阳子,黄侨,任远. 拱桥拱轴线的优化与选形[J]. 公路交通科技, 2007, 24(3):59-63.
LIN Yangzi, HUANG Qiao, REN Yuan. Optimization and selection of arch bridge axis[J].JournalofHighwayandTransportationResearchandDevelopment, 2007, 24(3):59-63.
[3] 李井辉,周厚斌,熊旭. 拱桥拱轴线两种优化方案比较[J]. 中外公路, 2008, 28(5):163-166.
LI Jinghui, ZHOU Houbin, XIONG Xu. Comparison of two optimization plans for the arch axes of arch bridges[J].JournalofChina&ForeignHighway, 2008, 28(5):163-166.
[4] 张佳. 拱轴线偏差对既有钢筋混凝土拱桥结构行为影响的研究[D].成都:西南交通大学, 2011.
ZHANG Jia.StudiesontheInfluencetotheExistedReinforcedConcreteArchBridgeStructureBehaviorofArchAxisVariation[D]. Chengdu:Southwest Jiaotong University, 2011.
[5] 陈生华. 石拱桥拱轴线偏位病害分析及加固方法研究[D]. 重庆:重庆交通大学, 2009.
CHEN Shenghua.StudyontheDeviationoftheArchAxisandStrengtheningMethodoftheStoneArchBridge[D]. Chongqing:Chongqing Jiaotong University, 2009.
[6] 刘山洪,李放,袁长红. 拱轴线横向偏离对拱圈静力行为影响[J]. 重庆交通大学学报(自然科学版), 2007, 26(1):14-18.
LIU Shanhong,LI Fang,YUAN Changhong. Influences of transverse bias of arch axis on the arch ring behavior under static loads[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2007, 26(1):14-18.
[7] 周建庭,邓智,袁瑞,等. 劣化拱轴线大跨石拱桥拱上建筑调载工序研究[J]. 重庆交通大学学报(自然科学版), 2010, 29(1):16-19.
ZHOU Jianting,DENG Zhi,YUAN Rui,et al. Adjusting load process of spandrel construction for large-span stone arch bridge with deteriorated arch axis[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2010, 29(1):16-19.
[8] 陈常明,杨玉凤,张连锋. 箱形拱桥拱轴线偏位内力影响分析[J]. 公路, 2013(8):117-121.
CHEN Changming, YANG Yufeng, ZHANG Lianfeng. Internal force effect analysis for the arch axis deviation in arch bridges[J].Highway, 2013(8):117-121.
[9] 乔奋义. 预应力折线形铰接钢拱加固拱桥技术研究[D]. 重庆:重庆交通大学, 2014.
QIAO Fenyi.ResearchonEnhancementofArchBridgeswithHingedPiecewiseSteelArchRings[D].Chongqing:Chongqing Jiaotong University, 2014.
[10] 章关永. 桥梁结构试验[ M] 北京:人民交通出版社, 2010.
ZHANG Guanyong.StructuralTestofBridge[M]. Beijing:China Communications Press, 2010.
[11] 过镇海. 钢筋混凝土原理[M]. 北京:清华大学出版社, 2013.
GUO Zhenhai.PrinciplesofReinforcedConcrete[M]. Beijing:Tsinghua University Press, 2013.
[12] 王贵明,彭文平,周超. 木蓬大桥高温合龙效应下拱圈内力调整研究[J]. 世界桥梁,2015(6):42-46.
WANG Guiming, PENG Wenping, ZHOU Chao. Study of internal force adjustment for arch ribs of mupeng bridge under high temperature closure effect[J].WorldBridges, 2015(6):42-46.
(责任编辑:朱汉容)
Strengthening Technique of Prestressing Hinged Piecewise Steel Arches for Arch Bridges
PENG Kai1,QIAO Fenyi2,JIA Xiaofei3
(1. School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, P. R. China; 2. Guangdong Nanyue Transportation Investment & Construction Co. Ltd., Guangzhou 510101, Guangdong, P. R. China; 3. Shenzhen Municipal Design & Research Institute Co. Ltd., Shenzhen 518029, Guangdong, P. R. China)
A scale-down RC structure model of the arch rib from an old bridge in Xinjiang province was designed and fabricated, then the model was tested and numerically simulated under the loading of structural self weight, respectively with or without the strengthening process by means of a prestressing hinged piecewise steel arch (PHPSA). The variation conditions of indicators, such as the stress, the deflection of controlling cross-sections and the bending energy of the arch model, were comparatively investigated before and after strengthening. The test results indicate that, the overall normal stress levels on the controlling cross-sections of the arch model after strengthening decrease a lot compared with those before strengthening; the PHPSA method could effectively modify the deformed axis of the arch model under the structural self weight; furthermore, the bending energy of the arch model after strengthening goes down by 81%. In general, the PHPSA used to strengthen the arch model effectively shares the structural internal forces and optimizes the structural stress condition under self weight, thus it greatly promotes the compressive carrying capacity of the arch under live load. This strengthening technique has a significant effect on those spandrel arch bridges with poor shapes of arch axes or in undue stress conditions under structural self weight loadings, so it makes a good choice for the technical decision on the rehabilitation of worn arch bridges.
bridge engineering; arch bridge strengthening; prestressing hinged piecewise steel arches (PHPSA); internal force optimization; arch axis modification; bending energy
10.3969/j.issn.1674-0696.2017.04.03
2016-03-21;
2016-05-21
彭 凯(1974—),男,重庆忠县人,副教授,硕士,主要从事桥梁及结构工程方面的研究。E-mail:piqueuni@163.com。
TU375.5
A
1674-0696(2017)04-012-06

