用数学眼光观察生活现象

用数学眼光观察生活现象

李中清

运算能力的训练与培养是初中数学学习的基本内容.在运算训练中，同学们要明白运算规则和方法，理解运算的算理，寻找合理简洁的运算途径来解决问题，并能结合自己的生活经历有所感悟.下面就幂的运算例谈数学学习与生活的联系.

一、次序性

例1计算：（-3x2）3∙x4-x4∙x6-（-2x5）2.

【解题策略】这是一道幂的混合运算问题，运算不难，按照运算规则：先算乘方，再算乘除，最后算加减，按序进行计算即可.

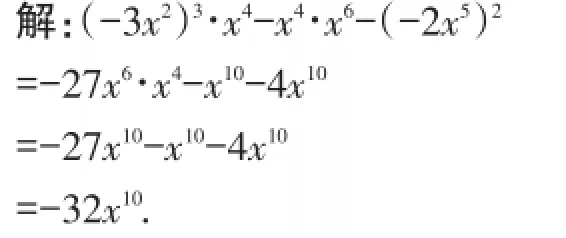
在具体运算中算“积的乘方”时，顺便将“同底数幂的乘法”也同时算出来了.

【生活启示】现实生活与数学学习一样，事情的发展是有先后次序的，不能改变，只能按照事物发展的次序拾级而上，就像例1中不能先算x4-x4一样.一个人的成长与发展，必须符合身心发展规律，不能随意改变.生活中很多事情不能同时完成，只能一件一件地做，而有的时候，在做一件事的同时，也可以顺便完成其他事情，就像例1中以减号为界分成三段，这三段可以同时计算.譬如，中午烧饭时，让电饭锅煮饭的同时可以洗菜、切菜等，统筹安排工作.

二、互逆性

例2计算：0.1254×（-8）3.

【解题策略】本题若先算乘方，再算乘法，是可以算出结果的，但比较繁琐，如果指数再大一些，就无法进行下去，如计算：0.1252017×（-8）2016.这时如何计算呢？我们可逆向思考，运算就大大简化了.在0.1252017×（-8）2016中，可以运用同底数幂的乘法运算的逆运算将0.1252017化为0.1252016×0.125，再逆用积的乘方，得到0.1252016×（-8）2016=［0.125×（-8）］2016=（-1）2016=1.到这里，答案就很显然了.这种思考问题的方法，使得运算简捷，同时也体现了解决一类问题的通法，当问题正向难以解决时，可以反过来思考，从而使问题得到解决.

【生活启示】生活中，有的事情一直往前冲，可以行得通，但有的事情按常规沿正向去做，可能困难重重，这时就要改变思考的方向，比如运用逆向思维，问题的解决可能就方便多了，逆向也是为了更好地前进.

三、整体性

例3已知am=12，an=2，求am-2n的值.

【解题策略】本题先要逆用同底数幂的除法，将am-2n改写成am÷a2n，再逆用幂的乘方，将a2n改写成（an）2，最后将am=12，an=2整体代入计算，从而问题得到解决.

【生活启示】在生活中，有时考虑问题，要考虑到每一个细节，分解而做；有时先要从整体把握，将整体分块解决.

四、思辨性

例4若（x+1）x+4=1，求x的值.

【解题策略】本题需要对底数和指数分别给予考虑，具体解答如下：

解：（1）当x+4=0，即x=-4时，x+1=-4+ 1=-3≠0，故当x=-4时，（x+1）x+4=1.

（2）当x+1=1，即x=0时，（x+1）x+4=1.

（3）当x+1=-1，即x=-2时，x+4=2（偶数），故当x=-2时，（x+1）x+4=1.

综合可知，x=0、-2和-4.

需要指出的是，许多同学在用“零指数幂的规定”时，仅得到第（1）种情形，显然在考虑问题时，认识不全面，理解不彻底.实际上，“1的任何次幂都等于1”及“-1的偶次幂等于1”这两种情况也要考虑，所以要运用分类讨论思想通盘考虑问题，注意要考虑问题的所有情况，并对每一种情况进行解答，同时要排除不符合题意的所有可能，做到不重不漏.

【生活启示】在解决一个生活中的复杂问题时，应将研究的问题分成若干相对简单的情况，做到不重不漏，然后对分出来的每一种情况进行逐个讨论，最后综合，从而使得整个问题得以解决.比如某公司某月销售业绩下滑，那么，就需要用分类讨论的方法，将公司经营的各个环节分解（生产、销售、售后），对成本、销售价格、费用等，逐个研究讨论，找出问题所在的根源.

学以致用，我们要在学习数学知识的同时，去关注自己的生活.用数学的眼光去观察生活中的现象，在生活中检验数学知识，并在生活中丰富自己的数学知识.

江苏省盐城市潘黄实验学校）

延伸阅读

幂与生活

随着社会的发展,幂运算在各个领域的应用非常广泛.生物芯片是20世纪80年代末在生命科学领域中迅速发展起来的一项高新技术.通俗地说，就是在一块指甲大小的芯片上集成大量探针单元，构成一个微型电子生物分析系统，以实现对生物样品准确、迅速、大信息量的检测.如果一块1.28×1.28平方厘米的芯片上集成了106个探针，你能知道每个探针单元的面积吗？这其中就蕴含着幂的运算方面的知识.

其实，这样的事例在生活中到处都有.比如，吃牛肉拉面时，要想知道拉面师傅拉面的条数，就要用到幂的运算；宇宙探索时，我们知道太阳光照射到地球表面所需的时间大约是5×102秒，光的速度大约是3× 108米/秒，那么地球与太阳之间的距离大约是多少千米呢？这些问题的解决都要用到幂的运算.