绝热毛细管基本流动模型的比较分析

陈鹏熙，张华

（上海理工大学能源与动力工程学院，上海 200093）

绝热毛细管基本流动模型的比较分析

陈鹏熙*，张华

（上海理工大学能源与动力工程学院，上海 200093）

毛细管在小型蒸汽压缩式制冷装置中起到降压、降温和调节流量的作用。在制冷系统的设计中，毛细管的长度和直径与制冷系统的匹配至关重要。传统的方法是通过查阅已编制的毛细管选型图表和经验公式，但结果很不准确且可选制冷剂种类很少，需要结合大量的实验才能确定毛细管的尺寸。经过大量研究，已发展出绝热毛细管内3种流动模型，即均相流动模型、分相流动模型和漂移流动模型。通过比较分析这3种基本流动模型，不仅给制冷系统中毛细管的选型和设计计算提供了参考，而且也为制冷系统的性能优化提供了方向。

绝热毛细管；模型；亚稳态；两相流

0 前言

毛细管作为节流机构在现代小型制冷设备中有着广泛的应用，这不仅得益于其简单易得的结构、低廉的制造成本，而且毛细管能够在制冷系统的高低压之间迅速建立起平衡，大大降低了压缩机的启动力矩。毛细管虽然能够与压缩机建立起流量平衡，但是无运动部件，不能根据负荷变化自动调节，且制冷剂在毛细管内的节流过程伴随着复杂的状态变化，这给制冷系统毛细管的尺寸匹配带来了困难。因此，合理匹配毛细管尺寸在制冷系统设计过程中显得尤其重要。根据《蒙特利尔议定书》和《京都议定书》的规定，CFC类制冷剂已被禁用，HCFC类制冷剂也在逐步被淘汰，制冷剂替代[1]工作正如火如荼地进行，但同时亦面临着新制冷剂与毛细管的匹配问题。工程上应用的毛细管[2-3]内径一般为(0.5～2) mm，长度为(2～6) m。过去，毛细管在制冷系统中的匹配工作主要通过实验的方法来进行，这既费时又费力。为了减少工作量，就需要对制冷剂在毛细管内的流动状态进行研究分析。从20世纪40年代开始，毛细管在实验与理论方面都有了很大的发展，得到了毛细管内流动状态的变化曲线[2]，如下图1。从不同研究者的研究成果来看，毛细管的研究方法主要采用均相流动模型、分相流动模型

1 均相流动模型

温度时,汽化滞后的热力学非平衡流动现象。COOPER等[8]通过实验观察到液相长度比理论计算的液相长度大，即使假设毛细管入口处局部损失为零也没有改善，因此得出结论：制冷剂的实际流动过程存在气化滞后。这是首次证实制冷剂流经毛细管时亚稳态流的存在。之后，各国学者也对亚稳态流展开了深入的研究。KOIZUMI和YOKOYAMA[9]也对毛细管进行了可视化研究,他们通过研究绝热毛细管长度方向上的压力和温度分布,证明了汽化延迟现象。HUERTA等[10]对影响亚稳态流动的因素进行了实验研究，结果指出毛细管入口的过冷度和制冷剂的质量流量对亚稳态区的长度影响较大，且研究得出，亚稳态区制冷剂液体的过热度随过冷度和质量流量的增大而减小；同时指出冷凝温度对过热度也有一定程度的影响，但影响较小。还有入口制冷剂的含油量会增大亚稳态区的长度。毛正荣等[11]对非共沸混合制冷剂R407C在毛细管内流动特性进行了研究和模拟计算。

对毛细管性能研究的一些理论模型及经验关联式与实际有一定的差距，重点在于无法准确预测真实汽化起始点，亚稳态段的存在会增加液体区的长度及质量流量。CHEN等[12]在1990年提出了计算实际汽化压力pvap的一个关联式：

该关联式是通过对R12的实验得出的。文献[12]中引用的一个估算汽化压力pvap的简单公式如下：

其中，系数kmeta=0.91～0.97，值得指出的是该公式是基于热水实验数据而得出，并未对制冷剂进行实验。

1.3 亚稳态两相区

对于亚稳态两相区的计算，FEBURIE等[13]提出将亚稳态两相区分为3种状态，即过热液体、饱和液体和饱和气体，并给出了一个经验关联式：

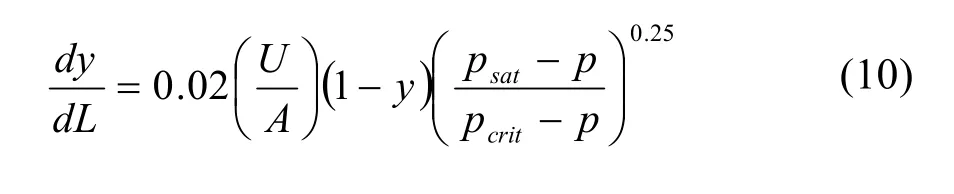
式中：

y——饱和相的质量分数，y=(ml+mg)/(ml+mg+mlm)。

在这3种状态中，过热液体的温度Tm被认为是恒定的，而饱和相的温度Tsat为压力的单值函数，平均温度定义为：T=(1–y)Tm+yTsat。

1.4 热力学平衡两相区

对于一个微元控制体，在运用一维能量守恒方程时，两相汽液混合物的比焓和比体积分别为：

两相流动的动量守恒方程仍然采用式(3)，其中两相摩擦因数ftp采用Lin等[14]提供的关联式：

公式中的A和B的定义与上面Churchill关联式中的定义相同。

WONG和OOI[15]基于均相流模型，利用Colebrook摩擦因子关联式，研究了6种两相粘度关联式对模型预测结果（压力分布）的影响。文献中同时指出，不同作者所提出的摩擦因子关联式应用于其他作者会产生较大的误差。结果表明，将DUKLER等提出的两相粘度关联式应用于均相流模型时会得到较优的预测结果。DUKLER等提出的两相粘度关联式如下[15]：

均相流动模型应用于绝热毛细管的计算相对简单，也因此得到了广泛运用。吕士济等[16]建立了绝热毛细管的一维均相模型，计算了传统制冷剂R12、R22及其替代制冷剂R134a、R152a在不同工况下毛细管的长度，同时还对这些制冷剂在不同工况下毛细管流动过程的热力性质变化进行了比较分析。王栋等[17]采用均相模型模拟了二氧化碳在毛细管内的流动曲线以及在不同的高压侧压力和气冷器出口温度下的流量特性曲线。陈铁光等[18]对考虑了亚稳态的绝热毛细管流动性能进行了理论研究，采用均相模型对绝热毛细管内的流体流动特性进行了模拟计算，并与实验结果比较，误差都在±10%以内。胡春霞等[19]在不考虑亚稳态段的情况下研究了非共沸混合制冷剂制冷系统毛细管长度的计算方法，并以非共沸混合制冷剂R134a/R23为例编制了毛细管长度计算程序，通过计算值与实验值的对比，误差不超过5%，证实了该计算方法的可行性。

2 分相流动模型

在两相流动中，由于气相与液相之间性质的差异（密度与粘度），气相与液相在管内的流动速度存在滑移，气相的流动速度大于液相的流动速度。在分相流模型中，定义了两个重要的参数，截面含气率（也称空隙率、空泡系数）和滑移比。

在气液两相流动的管道截面上，气相所占截面积Ag与总流通截面积A之比，称为截面含气率，用α表示，即α=Ag/A。这里需要与干度的定义区别，干度是气液两相流动中，气相的质量流量所占两相质量流量的份额，用x表示。将气相与液相的流速之比称为滑移比，用S表示，即S=Vg/Vl。截面含气率α与滑移比S和气相所占的质量流量份额x之间存在如下的关系：

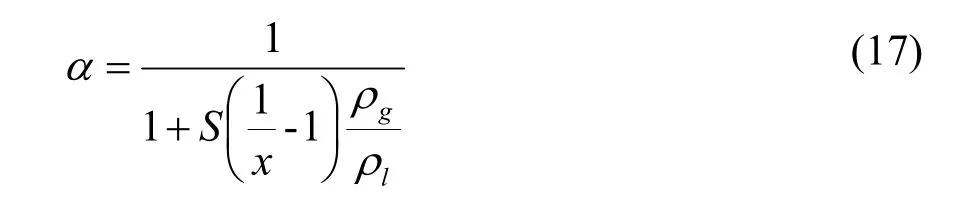
关于空泡系数的计算，前人已经做出了大量的研究，得到了许多有价值的经验关联式，并在工程中得到了广泛的应用。GHAJAR等[20]对水平管、倾斜管以及竖直管的有关空泡系数的关联式进行了最全面的分析和比较，得到并推荐了几种最有应用价值的关联式。在此基础上，分相流模型的能量方程可以写为：

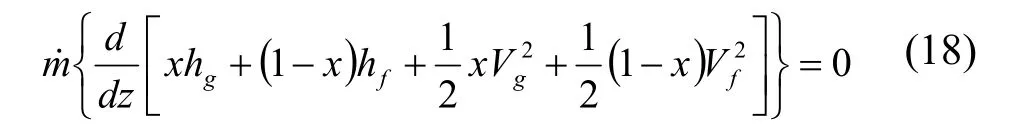
其中，气相和液相的流动平均速度计算公式为：

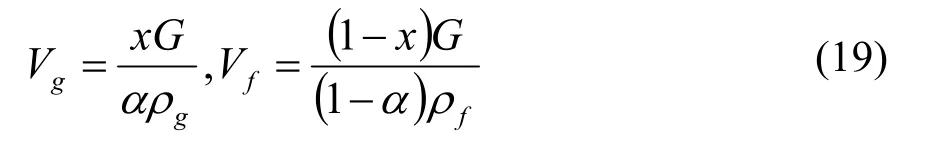
在分相流动中通常将压力降分成3个部分，即由流体加速引起的压力降、摩擦引起的压力降以及位能变化引起的压力降：

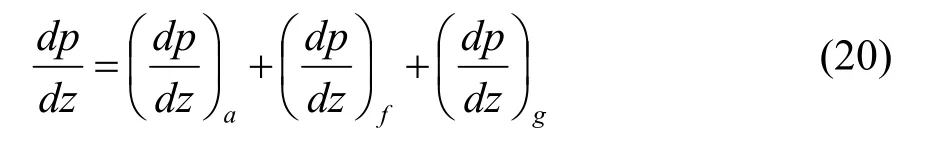
其中，在毛细管横截面积沿流动方向的高度变化可以忽略时，(dp/dz)g≈ 0。

由流体加速所引起的压力降可表示为：

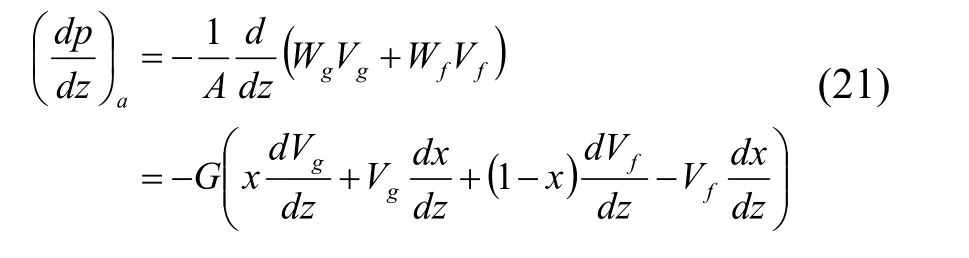
在两相流动中，焓值及比体积均仅为压力的函数。关于两相中的摩擦压力降，已经有大量的关联式可供选择，通常将摩擦压力降用乘积因子φ2表示，有以下3种形式：

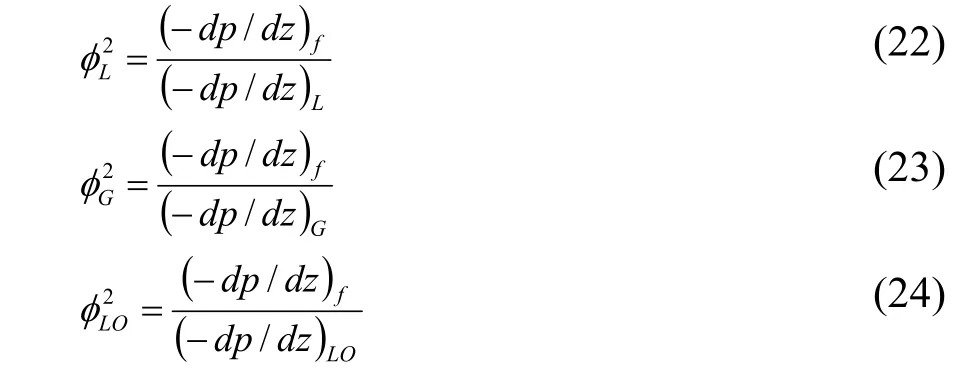
式中：

(−dp/dz)L——依据两相流动中由气相的平均流动速度计算的压力降；

(−dp/dz)G——依据两相流动中由液相的平均流动速度计算的压力降；

(−dp/dz)LO——与两相流动具有相同质量流率的液相的压力降。

文献中提供了多种关于乘积因子的计算式。

WONG和OOI[21]分析了均相流模型与分相流模型，并将两者的预测结果与实验数据比较，结果表明，分相流模型对压力分布以及干度的预测结果要比均相流模型好。

WONGWISES和CHAN[22]利用该分相流模型，分析了滑移比、摩擦因子、摩擦压力降和制冷剂类型对模型预测结果的影响，并对相应的制冷剂给出合适的滑移比、摩擦压力降和关联式。齐延峰等[23]利用分相流动模型研究了混合工质在绝热毛细管内的流动特性，并编制了计算程序，既可用于计算毛细管的长度和出口温度，也可以计算制冷剂的流量；作者通过实验，对理论计算模型进行了对比，结果偏差在10%以内。

近期，FURLONG等[24]分别应用均相流模型和分相流模型对R134a、R600a和R744在毛细管内的流动特性进行了研究，得出分相流模型比均相流模型有更高的拟合精度。

3 漂移流动模型

经过理论分析得出，尽管气液相间局部速度相等，实际气相的平均速度和液相的平均速度并不相等，存在一定的漂移速度。ZUBER和FINDLEY[25]首次提出了基于两相漂移速度的漂移流模型。所谓的漂移流模型，实质上是分相流动的一种特殊模型，它把注意力集中在两相的相对运动上，而不描述每一相的运动。流体在通道内的局部相速度和局部含气率是有变化的，在整个通道内局部相速度可能会相等，而局部含气率和局部相速度分布的不同会导致滑移比并不等于1。漂移流模型考虑了两个影响因素对空隙率的影响：一个是两相间相对速度，另一个是空隙率和流速沿截面的分布规律。

通过将有关的流动参数在整个流通横截面求得平均值，流体在管道内的三维流动便可简化为准一维的流动。通常将流动参数在横截面上进行积分，并求其在整个横截面上的平均值，即：

式中：

F——局部参数的一般函数；

设局部空隙率为α，则任意参数F的加权平均值定义为：

其中，k表示液相（k=f）或气相（k=g）。

由于管道直径很小，沿横截面的压力降可以忽略，因此在横截面上气相及液相的密度可以认为是常数，即

两相混合物的平均密度可以表示为：

截面上每一相的加权平均速度可以表示为：

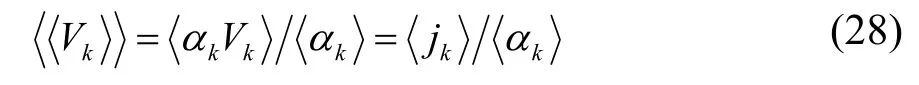
其中j为体积流率，

同时定义两相混合物的平均流速为：

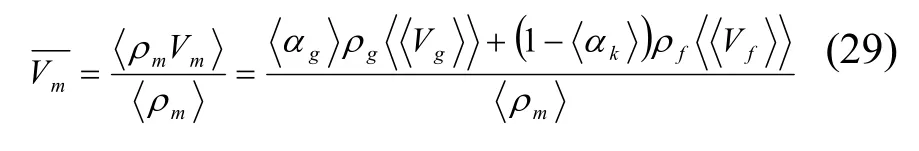
根据平均流速的2种定义，气相的漂移速度可以表示为以下2种形式：

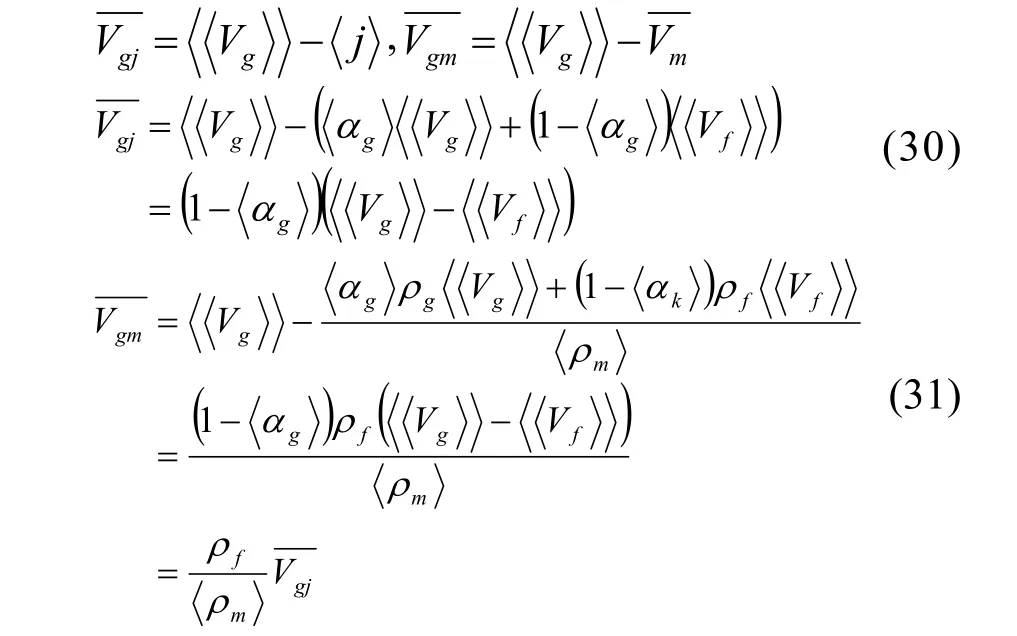
因此，可得到气相及液相的平均速度：

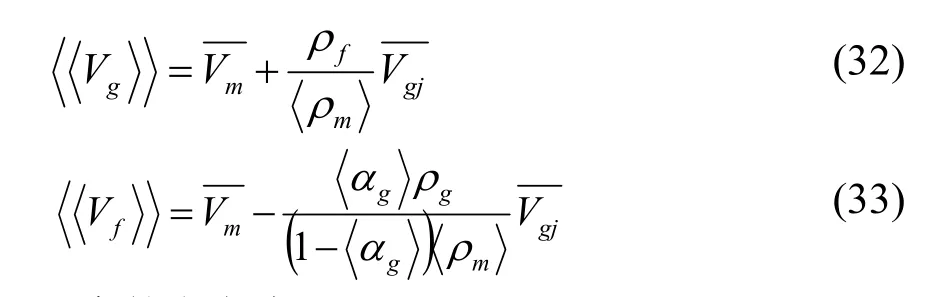
干度的定义为：

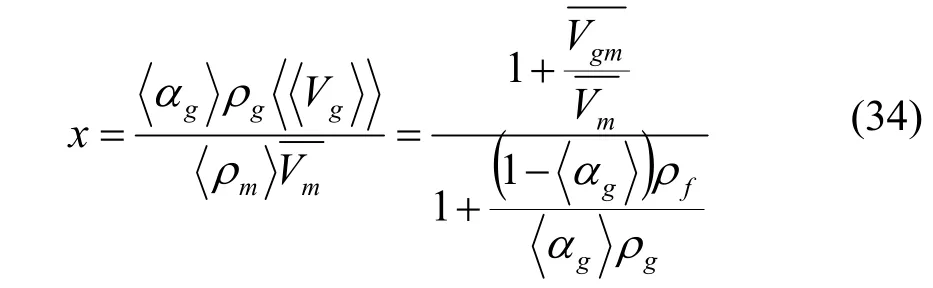
由上面的变量定义，（假设）可以得到流动的控制方程形式。

连续性方程：

动量方程：

能量方程：

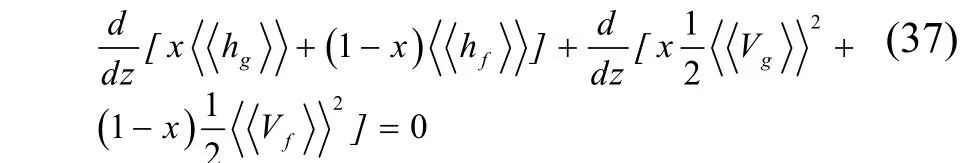
除上述3个方程外还需要漂移速度方程，由ZUBER和FINDLAY[25]给出的关联式：

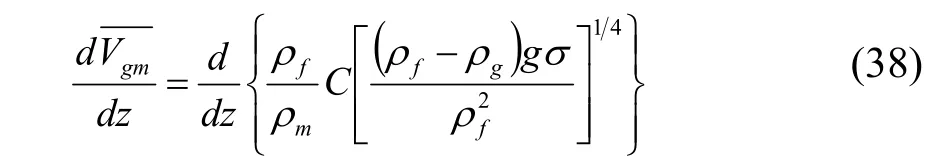
将漂移流模型应用于毛细管仍是一个新的尝试，这主要是漂移速度的关联式缺乏实验数据。LIANG和WONG[26]利用该漂移流模型进行毛细管的仿真计算，并将预测结果与LI等[12]对R12在毛细管内的流动所测得的实验数据进行比较，结果表明，该漂移流模型应用于毛细管的仿真计算有较高的精度。同时，应用该模型预测了R134a在毛细管内的流动特性（包括压力分布、干度、空泡系数、相速度及相对漂移速度）。

4 结论与展望

1）流体流经毛细管时实际上存在亚稳态流动现象，在不考虑亚稳态流动时的长度误差最大可达到25%。对亚稳态流动现象需进行深入的研究，因为至今仍没有一个通用的关联式用于汽化起始点的估算。

2）分相流动模型与漂移流动模型对气液两相流动状态的描述更合理一些，计算得到的结果也比均相流动模型有较高的精度，虽是新的尝试，却有很好的发展前景，仍需要不断的改进完善；然而通过对摩擦系数关联式与两相粘度关联式的不断修正，应用均相流动模型会更加简便，误差保持在±10%以内。

3）应用各种流动模型进行毛细管的选型计算需要不断地改进优化算法，程序化是未来的发展方向。

[1] 李连生. 制冷剂替代技术研究进展及发展趋势[J]. 制冷学报, 2011, 32(6): 53-58.

[2] 郭宪民. 带毛细管的小型制冷机工作效率的提高[J].制冷技术, 1997, 17(4): 30-31.

[3] 童蕾, 陈超敏. 对冰箱制冷系统中毛细管的探讨和分析[J]. 制冷技术, 2004, 24(3): 11-13, 18.

[4] 王江翠, 金晓辰, 邵亮亮, 等. 绝热毛细管无量纲流量关联式评估[J]. 制冷技术, 2011, 31(3): 30-33.

[5] 樊海彬, 任悦, 周全. 绝热毛细管数学模型的建立与分析[J]. 制冷空调与电力机械, 2006, 27(6): 14-17.

[6] BANSAL P K, RUPASINGHE A S. An homogenous model for adiabatic capillary tubes[J]. Applied Thermal Engineering, 1997, 18(3): 207-219.

[7] 陈之航, 曹柏林, 赵在三. 气液两相流动和传热[M].机械工业出版社, 1982: 63-64.

[8] COOPER L, CHU C K, BRESKEN W R. Simple selection method for capillaries derive from physical flow conditions[J]. Refrigerating Engineering, 1957, 65(7): 37-41.

[9] HISAO K, KUNIO Y. Characteristics of refrigerant flow in a capillary tube[J]. ASHRAE Transactions, 1957, 86(2): 19-27.

[10] SILVA H A A, SANZOVOFIORELLI F A, ODEMATTOS S. Meta-stable flow capillary tubes: An experimental evaluation[J]. Experimental Thermal and Fluid Science, 2007, 31(8): 957-966.

[11] 毛正荣, 武卫东, 张华. 非共沸工质在毛细管的流动特性研究[J]. 制冷技术, 2003, 23(4): 42-50.

[12] CHEN Z H, LI R Y, LIN S, et al. A Correlation for meta-stable flow of refrigerant 12 through capillary tubes[J]. ASHRAE Trans, 1990, 96(1): 550-554.

[13] FEBURIE V, GIOT M, GRANGER S, et al. A model For Choked flow through cracks with inlet sub-cooling[J]. International Journal of Multiphase Flow, 1993, 19(4): 541-562.

[14] LIN S, KWOK C C, LI R Y，et al. Local frictional pressure drop during vaporization of R12 through capillary tubes[J]. International Journal of Multiphase Flow, 1991, 17(1): 95-102.

[15] WONG T N, OOI K T. Refrigerant flow in capillary tube：An assessment of the two phase viscosity correlations on model prediction[J]. International Communications in Heat and Mass Transfer, 1995, 22(4): 595-604.

[16] 吕士济, 何茂刚, 范德勤, 等. 替代制冷剂在绝热毛细管中流动的数值计算[J]. 工程热物理学报, 2006, 27(3): 365-368.

[17] 王栋, 李蒙, 戚利利, 等. 二氧化碳制冷系统毛细管的设计及实验研究[J]. 化工学报, 2011, 62(10): 2753-2758.

[18] 陈轶光, 杨昭, 任勇. 考虑亚稳态的绝热毛细管流动性能的理论研究[J]. 低温与超导, 2009, 37(10): 40-45.

[19] 胡春霞, 时阳, 丁瑞华. 自行复叠式制冷系统毛细管的计算[J]. 郑州轻工业学院学报, 2006, 21(4): 58-61.

[20] WOLDESEMAYAT M A, GHAJAR A J. Comparison of void fraction correlations for different flow patterns in horizontal and upward inclined pipes[J]. International Journal of Multiphase Flow, 2007, 33(4): 347-370.

[21] WONG T N, OOI K T. Adiabatic capillary tube expansion devices：A comparison of the homogeneous flow and the separated flow models[J]. Applied Thermal Engineering, 1996, 16(7): 625-634.

[22] WONGWISES S, CHAN P, LUESUWANATAT N, et al. Two-phase separated flow model of refrigerants flowing through capillary tubes[J]. International Communications in Heat and Mass Transfer, 2000, 27(3): 343-356.

[23] 齐延峰, 公茂琼, 孙兆虎, 等. 混合工质在制冷机节流元件毛细管中的流动特性[J]. 天然气工业, 2004, 24(12): 139-141.

[24] FURLONG T W, SCHMIDT D P. A comparison of Homogenous and separated flow assumptions for adiabatic capillary flow[J]. Applied Thermal Engineering, 2012, 48: 186-193.

[25] ZUBER N, FINDLEY J A. Average volumetric concentration in two-phase flow systems[J]. Heat Transfer, 1965, 87(4): 453-468.

[26] LIANG S M, WONG T N. Numerical modeling of two phase refrigerant flow through adiabatic capillary tubes[J]. Applied Thermal Engineering, 2001, 21(10): 1035-1048.

Comparison and Analysis of Basic Flow Models for Adiabatic Capillary Tubes

CHEN Pengxi*, ZHANG Hua
(School of Energy and Power Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

Capillary tubes in small-scale vapor compression refrigeration systems are applied for decreasing pressure and temperature and controlling refrigerant flux. The length and diameter of capillary tubes matched to the refrigeration system are crucially important for the design of the refrigeration system. The traditional way of selecting an appropriate capillary tube is to look up charts and tables and some empirical correlations. Since the results through these ways are not accurate and the alternative refrigerants are not enough, the dimension of the capillary tube can be finally determined by amounts of experiments. Based on considerable investigations, three flow models for adiabatic capillary tubes have been developed, namely, the homogeneous flow model, separated flow model and drift flow model. Comparison and analysis on these three basic flow models are performed, providing a reference of selection and design calculation of the capillary tubes and a possible way to optimize the performance of the refrigeration systems.

Adiabatic capillary tubes; Models; Metastable; Two phase flow

10.3969/j.issn.2095-4468.2017.01.205

*陈鹏熙，男（1991-），硕士在读。研究方向：低温设备，制冷系统仿真。联系地址：上海市杨浦区军工路516号上海理工大学制冷及低温工程实验室，邮编：200093。联系电话：13061818132。E-mail：pengxichen725@163.com。