扇翼飞行器短距起飞性能
孟 琳,叶永强
(南京航空航天大学 自动化学院, 南京 211106)
扇翼飞行器短距起飞性能
孟 琳,叶永强
(南京航空航天大学 自动化学院, 南京 211106)
为验证扇翼飞行器超短距起飞特性及大载荷特性.以某型6 kg级扇翼飞行器为研究对象,在分析其结构特点和飞行原理的基础上,根据该飞行器在地面与空中的受力情况,建立了扇翼飞行器的纵向模型,使地面滑跑段与空中段有效衔接,并通过数值仿真,对比分析了升降舵偏转量、重心位置、扇翼转速以及载荷量对扇翼飞行器起飞滑跑距离的影响.仿真结果表明:空载时起飞滑跑距离最短;在起飞过程中需要保持升降舵上偏最大角度;重心位置越靠近扇翼力作用点,起飞滑跑距离越短;在这些因素固定的情况下配合适当扇翼转速,最终获得该样机不到9 m的最短起飞滑跑距离.通过对比分析,良好的起飞性能需要几个因素的配合设置.
扇翼飞行器;短距起降;大载荷;飞行原理;纵向建模
1962年皮特·道尼尔(Peter Dornier)[1-2]提出了一种将横流式风扇嵌入到固定翼飞机机翼中,通过扇翼转动来提供飞行动力的飞机结构.1998年,皮布尔斯[3](Peebles)完成了扇翼飞行器首次成功试飞,并通过风洞试验验证了横流式风扇作为飞机动力源的可行性.作为一种介于直升机和固定翼飞机之间的低速大载荷飞行器,扇翼飞行器因其优越的飞行性能[4],受到广泛关注.扇翼飞行器的发展主要分为两个阶段:2006年以前科学家们致力于用试验验证扇翼飞行器的可行性和优越性[5-6](如短距起降、低速大载荷以及大迎角飞行不失速等);2006年以后,科学家们开始利用先进计算机技术来优化传统的扇翼模型,并提出切实有效提升扇翼飞行器飞行性能的结构创新[7-8](如高平尾和双尾翼可以减小气动干扰;远置舵面可以增加扇翼飞行器的低速操作功效等).国内扇翼飞行器起步较晚,至今仅存在于部分研究所和高校:中国航空工业空气动力研究院[9-10]、南京航空航天大学[11-13]、华东理工大学[14].目前学者们致力于通过高精度CFD (computational fluid dynamics—计算流体动力学)数值模拟技术,对扇翼飞行器特殊的原理进行数值模拟分析[15-17],利用控制横流式风扇内部偏心涡的强度和位置,来控制扇翼产生的升力和推力,从而优化扇翼飞行器的飞行性能[18].但是很少有人通过飞行器其他结构设计的改进以及飞行控制来更好地实现其超短距起降等优越性能的优化.
1 扇翼飞行器的飞行原理
扇翼飞行器的扇翼是由可转动的水平转子叶轮以及半包裹它的固定翼两部分共同组成,用以同时提供升力和推力.其工作原理如图1所示.
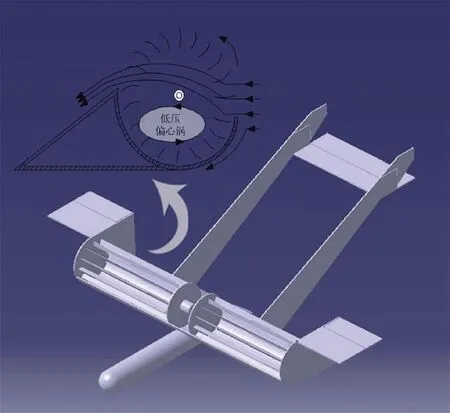
图1 扇翼结构
由图1扇翼机构图可知,扇翼飞行器是根据马格努斯效应制造而成的:当气流沿着一个旋转物体的旋转平面流过时,会在物体上产生一个垂直于气流流向的作用力.扇翼机在机翼上装配水平轴向转动的横流式风扇,通过扇翼的主动旋转,在机翼前缘抽空空气,通过叶片的旋转使扇翼上表面气流得到加速,从而形成压力差,进而产生部分升力,这部分升力产生机理与固定翼飞机飞行原理相同.而不同于传统固定翼飞机,扇翼机80%的升力来源于低压偏心涡[14].扇翼转动时,风扇内部产生强有力的偏心涡[19],形成低压区,使得机翼前半部分圆弧形区域的上、下表面产生较大压力差,从而产生升力.
扇翼飞行器获得的推力也可以分为两部分:一部分推力由牛顿第三定律获得,扇翼转动时,叶片推动气流向后排出,从而获得向前的反推力;另一部分推力也是由低压偏心涡提供的,由于偏心涡大多形成于叶片内部偏左下方的位置,这就影响了机翼内部的压强分布[20],从而获得另一部分推力.
2 扇翼飞行器的纵向建模
模型建立是进行扇翼飞行器起飞性能测试的基础,飞行器在地面滑跑时,地面效应对其起飞性能存在影响,所以在起飞建模过程中考虑地效影响,这样可以更加真实的反应飞行器起飞过程.由于起飞只涉及纵向特性,所以只对扇翼飞行器的纵向进行建模.本文以某重6 kg扇翼机为测试模型,不采用传统的分段建模,而是将各个飞行阶段在一个模型中表现出来,关键是判断地面对轮子的支反力[21].本文将模型分为四轮滑跑段、后轮滑跑段以及空中段3个阶段[22].不同于普通固定翼飞机,扇翼机主要升力通过扇翼转动获得,因此不需要像普通固定翼飞机一样通过抬头增大飞行迎角来增加起飞所需升力.因扇翼机起飞时需要较大的升力,高速转动的扇翼产生升力的同时伴随着较大的低头力矩,因此,该扇翼机模型是低头起飞,后面两个轮子先离地,这是有别与于传统固定翼飞机的特殊之处.本文中模型的建立是在苏式坐标系基础上进行的.
2.1 机轮产生的力与力矩
为简化模型,假设机轮不受横侧向的力和力矩,且前后轮的摩擦系数相同,记为fx.飞机起飞时,机轮受到地面的支反力和摩擦力,受力分析如图2所示.
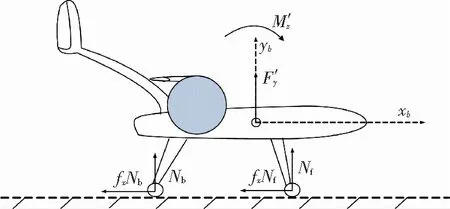
图2 扇翼飞行器起飞滑跑段受力分析
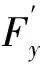
(1)
式中:Xfgear、Xbgear分别为前、后轮支反力力臂;Ygear为前、后轮摩擦力力臂.由式(1)可得前、后轮滑跑阶段前、后轮支反力的表达式如下:
(2)
随着滑跑速度的增加,扇翼机后轮抬起,进入前轮滑跑阶段,此时,由式(2)得到前、后轮的支反力计算如下:
进入前轮滑跑阶段后,扇翼机所受升力逐渐加大,地面对前轮的支反力逐渐减少.当主轮离地时,飞行器离地进入空中飞行阶段.此时有
综上所述,两个机轮产生的合力与合力矩在机体坐标系中分量的输出如下:
式中:Fx_wheel、Fy_wheel、Fz_wheel分别为两个机轮产生的合力在机体坐标系3个轴上的分量;Mx_wheel、My_wheel、Mz_wheel分别为两个机轮产生的合力矩在机体坐标系3个轴上的分量.这里机轮支反力只有在起飞和着陆的时候会用到,通过模型的转换,将地面支反力加入总的力与力矩的计算中.
2.2 扇翼飞行器纵向建模
扇翼飞行器整体受力情况与传统固定翼飞机相似,因此,纵向模型也是借鉴传统固定翼飞机进行的,得到扇翼飞行器纵向运动方程组[23]为
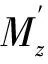
3 扇翼飞行器短距起飞特性分析
扇翼飞行器兼顾了固定翼飞机和直升机的优越性能,其中最为突出的性能就是短距起降和低速大载荷的特性.本文先以该扇翼飞行器空载模型进行测试,着重研究扇翼飞行器俯仰舵面偏转量、重心位置以及扇翼转速对扇翼飞行器起飞滑跑距离的影响,为扇翼飞行器的结构设计和飞行控制提供理论依据.
首先,保持重心位置为xcg=0.5 m(距离机头的距离),横流风扇的转速δn=2 500 r/min,舵面偏转分别取δe=-20°/-24°/-28°/-32°,得到舵面偏转量对于扇翼飞行器滑跑距离和起飞高度的影响,如图3,4所示.
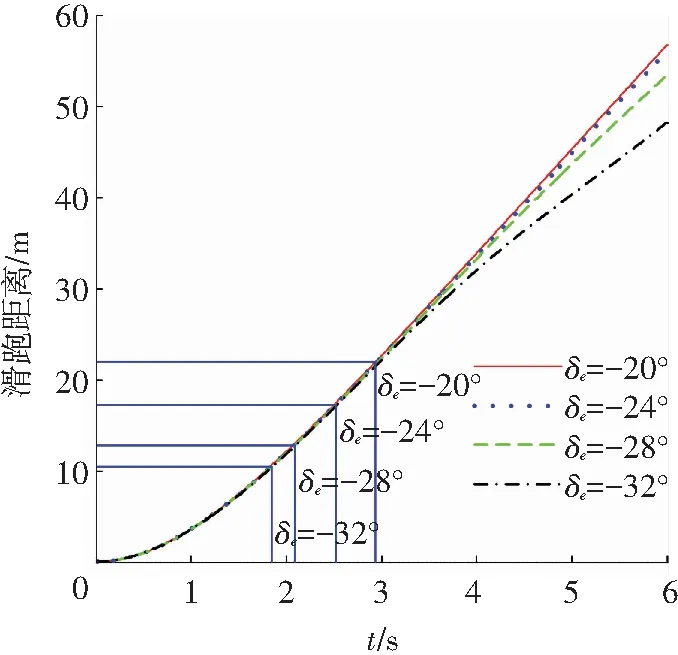
图3 升降舵偏转量对滑跑距离的影响
Fig.3 Changes in the take-off distance influenced by the elevator deflection

图4 升降舵偏转量对飞行高度的影响
Fig.4 Changes in the flight altitude influenced by the elevator deflection
从图4可以看出,升降舵上偏的角度越大越有利于飞行器起飞,因为升降舵偏转越大,会相应产生较大的抬头力矩,弥补因扇翼转动而附加的低头力矩,使飞行器更快抬头起飞,因此在起飞阶段应该将俯仰舵面打到允许的最大舵偏角.这里为了保持升降舵偏转在起飞时刻留有一定余量,取舵面偏转δe=-30°.
其次,已知该模型扇翼作用点在距离机头0.54 m的位置,保持升降舵偏角为δe=-30°,扇翼转速δn=2 500 r/min,分别取重心位置xcg=0.48/0.49/0.50/0.51 m,得到其对扇翼飞行器滑跑距离和起飞高度的影响, 如图5,6所示.

图5 重心位置对滑跑距离的影响
Fig.5 Changes in the take-off distance influenced by the position of the center of gravity
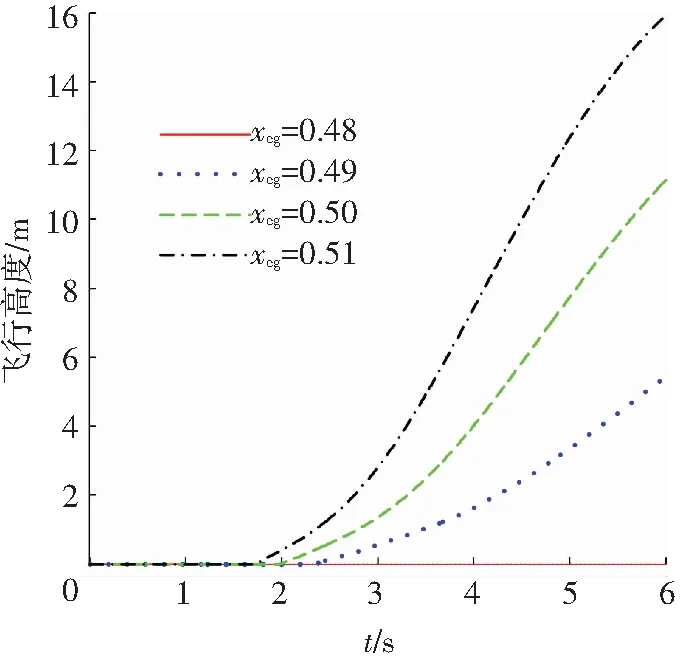
图6 重心位置对飞行高度的影响
Fig.6 Changes in the flight altitude influenced by the position of the center of gravity
从图6可知,重心位置越靠近扇翼升力作用点,飞机越容易起飞.当重心靠近扇翼升力作用点时,扇翼转动附加的低头力矩相应减小,此时相同偏转舵面和扇翼转速的情况下,飞行器更容易起飞.因此,在舵面偏转和转速不变情况下,当前扇翼飞行器模型的重心应该尽量靠近扇翼作用点配置,但是在该飞行器模型中,重心靠近扇翼作用点太近,也同时拉近了重心和气动中心的距离,会导致飞行器静不稳定,因此,本文取xcg=0.51 m为最佳.
最后,保持升降舵偏转角度为δe=-30°,取重心位置为xcg=0.51 m,取扇翼的转速分别为δn=2 400/2 500/2 600/2 700 r/min,得到其对扇翼飞行器滑跑距离和起飞高度的影响,如图7,8所示.
图8中分别选取转速为2 400~2 700 r/min,即飞行器能够起飞的转速.若起飞阶段扇翼转速过小,产生的升力不足,导致飞机难以起飞,因此从2 400 r/min开始进行起飞性能测试.当转速为2 400 r/min时,扇翼飞行器可以相对快速起飞,但是起飞5 s后,飞行高度瞬间减小,这是因为较大的舵面偏转产生大的抬头力矩,虽然飞行器可以快速抬头起飞,但是由于这个大抬头力矩使飞行器抬头翻滚,进而坠落.当转速大于2 500 r/min的时候,起飞滑跑距离变长.随着转速的增大,伴随着越来越大的低头力矩,当转速达到2 700 r/min时,由于扇翼转动的附加低头力矩太大,最终导致飞行器机头触地,而无法正常起飞.因此最佳扇翼转速的选取,是根据当前舵面偏转量以及重心位置综合考虑的结果,这里最佳转速为2 500 r/min.
3组数据每组的测试参数以及最佳滑跑距离见表1.
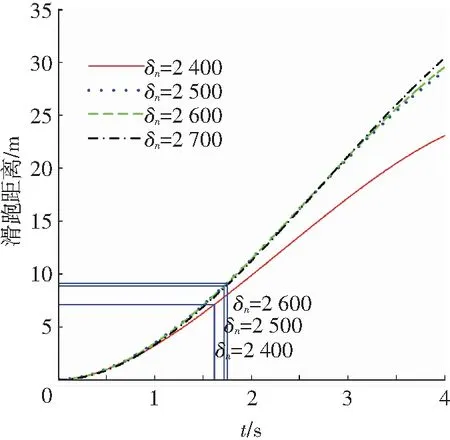
图7 扇翼转速对滑跑距离的影响
Fig.7 Changes in the take-off distance influenced by the fan wing rotation speed
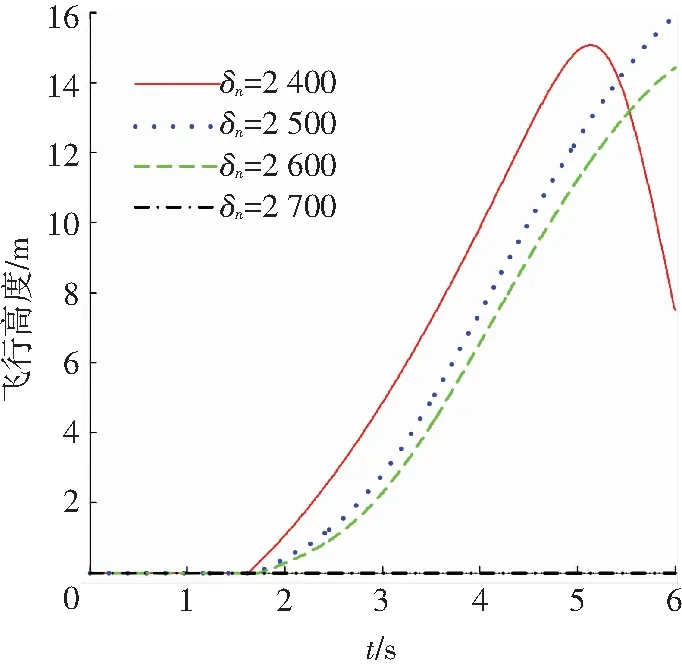
图8 扇翼转速对飞行高度的影响
Fig.8 Changes in the flight altitude influenced by the fan wing rotation speed

表1 最佳滑跑距离
虽然转速为2 400 r/min时,扇翼飞行器可以相对快速起飞,但是起飞5 s后,由于舵面偏转产生较大抬头力矩使飞行器抬头翻滚,进而坠落.当升降舵偏转δe=-30°、重心位置xcg=0.51 m、扇翼转速δn=2 500 r/min情况下,扇翼飞行器1.72 s后起飞,此时起飞滑跑距离小于9 m.以该最短滑跑距离的3个因素取值为基准,在δe、xcg、δn中,各变动1个因素,3个因素的不同组合对滑跑距离和飞行高度的影响,取值见表2.

表2 3个因素取值组合
3个因素组合影响对比图如图9,10所示.

图9 不同δe、xcg、δn组合下的滑跑距离
Fig.9 Taking-off distance influenced by different combinations ofδe,xcgandδn
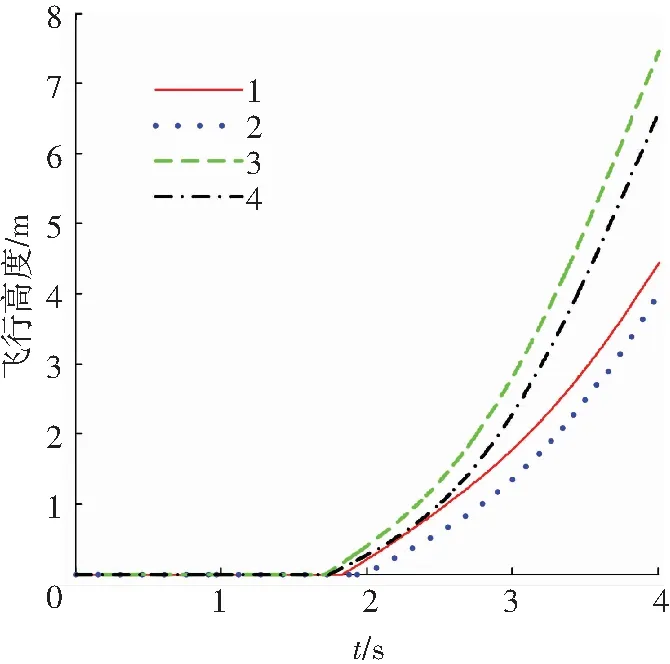
图10 不同δe、xcg、δn组合下的飞行高度
Fig.10 Flight altitude influenced by different combinations ofδe,xcgandδn
图10中可以看出重心位置对扇翼飞行器起飞滑跑距离影响最为显著,因扇翼转动是该飞行器主要升力来源,重心位置的变化改变了扇翼转动产生的低头力矩的力臂,进而直接影响到扇翼飞行器的起飞状态.而扇翼转速和升降舵作用是相辅相成的,扇翼转速的增大使得扇翼飞行器受到升力增加的同时也加大了其受到的低头力矩,此时需要较大的升降舵偏转来提供一定的抬头力矩,若提供的抬头力矩不足则飞行器低头触地无法起飞,抬头力矩太大则导致飞行器起飞之后侧翻,同样无法快速安全起飞.因此在保证飞行器安全起飞的前提下取得δn和δe的最优组合,从而获得最佳起飞状态量.
然后,在上述最佳参数的基础上,即保持升降舵偏转角度为δe=-30°,重心位置为xcg=0.51 m,扇翼转速为δn=2 500 r/min,测试扇翼飞行器载荷量对其起飞性能的影响.这里分别取空载到载重3 kg进行测试,即飞行器起飞质量分别取weight=6/7/8/9 kg,得到载荷量对滑跑距离和起飞高度的影响,图11、12所示.
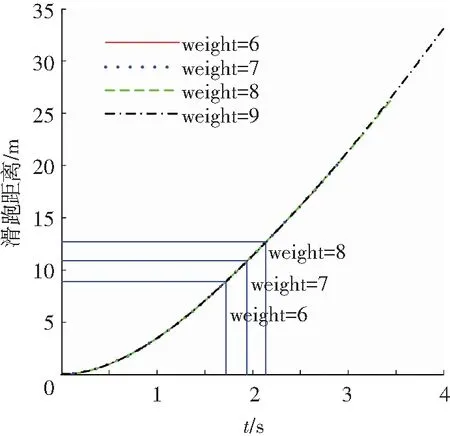
图11 飞行器载荷量对滑跑距离的影响
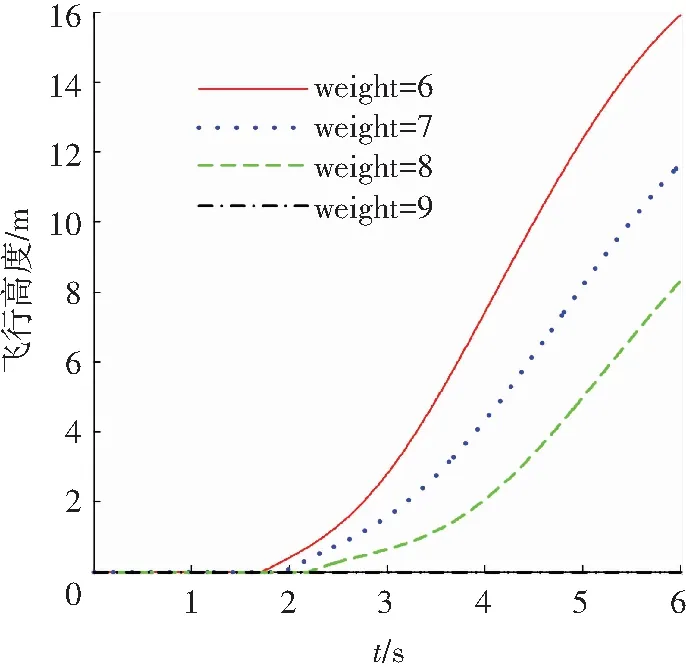
图12 飞行器载荷量对飞行高度的影响
从图11、12可以看出,载重越大,扇翼飞行器起飞滑跑距离越远,当载重达到3 kg时,扇翼飞行器无法正常起飞.测试表明6 kg重扇翼飞行器最大可载重2 kg实现起飞,是其本身质量的1/3,这也验证了扇翼飞行器载荷大的特性.
4 结 论
1)重心位置应尽量靠近扇翼作用点,以减小起飞时因扇翼转动而附加的低头力矩;同时在起飞时应尽量将升降舵面向上偏转最大角度,用以弥补扇翼转动带来的低头力矩;扇翼转速应尽量打到最大值,以提高扇翼飞行器起飞时的升力.
2)当舵面偏转取δe=-30°,重心位置取xcg=0.51 m,扇翼转速取δn=2 500 r/min 时,最短起飞滑跑距离小于9 m.仿真表明, 该型扇翼飞行器可载重相当于本身质量1/3的负荷飞行,验证了其大载荷的特性.本文的研究为扇翼飞行器结构设计和飞行控制提供了指导.
[1] DORNIER P. Multiple drive for aircraft having wings provided with transverse flow blowers: US Patent 3065928 [P]. 1962-11-27.
[2] DORNIER P. Aircraft with ground effect landing gear: US Patent 3082976 [P]. 1963-3-26.
[3] PEEBLES P. Aerodynamic lift generating device: US Patent 6527229B1[P]. 2003-3-4.
[4] 牛中国, 蒋甲利, 刘杰, 等. 扇翼飞行器机翼设计与研究[J]. 气动研究与实验, 2009, 27(3): 6-11. NIU Zhongguo, JIANG Jiali, LIU Jie, et al. Design and research of fan-wing Airfoil [J]. Aerodynamic Research & Experiment, 2009, 27(3): 6-11.
[5] FORESHAW S. Wind tunnel investigation of the new ‘Fanwing’ design [R], Wales: Report to FanWing Ltd. 1999.
[6] AHAD O, GRAHAM J M R. Flight simulation and testing of the Fanwing experimental aircraft[J]. Aircraft Engineering and Aerospace Technology, 2007, 79(2): 131-136. DOI: 10.1108/00022660710732671.
[7] KUMMER J D, DANG T Q. Hight-lift propulsive airfoil with integrated cross flow fan [J]. AIAA Journal of Aircraft, 2006, 43(4): 1059-1068. DOI: 10.2514/1.17610.
[8] SEYFANG G R. Fanwing-developments and applications[C]//Proceedings of the 28th International Congress of the Aeronautical Sciences. [S.l.]: ICAS, 2012: 1-9.
[9] 牛中国, 蒋甲利, 李周复. 扇翼飞行器风扇叶片偏角影响数值分析[J]. 气动研究与实验, 2008, 26(2): 6-10. NIU Zhongguo, JIANG Jiali, LI Zhoufu. Numerical analysis of fan-wing fan blades angle[J]. Aerodynamic Research & Experiment, 2008, 26(2): 6-10.
[10]蒋甲利, 牛中国, 刘捷, 等. 扇翼飞行器机翼布局研究[J]. 航空科学技术, 2009 (3): 30-35. DOI: 10.3969/j.issn.1007-5453.2009.03.009. JIANG Jiali, NIU Zhongguo, LIU Jie, et al. Research on the Wing Composition of Fanwing Flight[J]. Aeronautical Science and Technology, 2009 (3): 30-35. DOI: 10.3969/j.issn.1007-5453.2009.03.009.
[11]黄同高, 杨忠, 王仁华, 等. 扇翼飞行器纵向运动建模与控制方法[J]. 应用科技, 2011, 38(11): 5-8. DOI: 10.3969/j.issn.1009-671X.2011.11.002. HUANG Tonggao, YANG Zhong, WANG Renhua, et al. Longitudinal mathematical modeling and flight control of the fanwing aircraft[J]. Applied Science and Technology, 2011, 38(11): 5-8. DOI: 10.3969/j.issn.1009-671X.2011.11.002.
[12]王仁华, 张海黎, 黄同高, 等. 扇翼飞行器绕翼型流动数值研究[J]. 应用科技, 2012, 38(12): 5-8. DOI: 10.3969/j.issn.1009-671X.2011.12.002. WANG Renhua, ZHANG Haili, HUANG Tonggao,et al. Numerical study of flow over fan-wing airfoil[J]. Applied Science and Technology, 2012, 38(12): 5-8. DOI: 10.3969/j.issn.1009-671X.2011.12.002.
[13]杜思亮, 唐正飞. 四扇翼无人飞行器及控制方法: CN104401485A [P]. 2015. DU Siliang, TANG Zhengfei. An unmanned aerial vehicle with four fan-wings and its control method: CN104401485A [P]. 2015.
[14]邸南思.面向飞行机器人的扇翼翼型数值分析与实验研究[D]. 上海: 华东理工大学, 2014. DI Nansi. Computational simulation and experimental research on fan wing for flying robot[D]. Shanghai: East China University of Science and Technology, 2014.
[15]DUDDEMPUDI D, YAO Yufeng, EDMONDSON D, et al. Computational study of flow over generic fan-wing airfoil [J]. Aircraft Engineering and Aerospace Technology, 2007, 79(3): 238-244. DOI: 10.1108/00022660710743831.
[16]ASKARI S, SHOJAEEFARD M H. Numerical simulation of flow over an airfoil with a cross flow fan as a lift generating member in a new aircraft model [J]. Aircraft Engineering and Aerospace Technology, 2009, 81(1): 59-64.DOI: 10.1108/00022660910927466.
[17]ASKARI S, SHOJAEEFARD M H. Shape optimization of the airfoil comprising a cross flow fan [J]. Aircraft Engineering and Aerospace Technology, 2009, 81(5): 407-415. DOI: 10.1108/00022660910983680.
[18]SARACOGLU B H. Analysis of the flow flied around the wing section of a FanWing aircraft under various flow conditions[C]// Proceedings of the 53rd AIAA Aerospace Sciences Meeting. Kissimmee, Florida: AIAA, 2015: 5-9. DOI: 10.2514/6.2015-1936.
[19]DANG T Q, Bushnell P R. Aerodynamics of cross-flow fans and their application to aircraft propulsion and flow control [J]. Progress in Aerospace Sciences, 2009, 45(1/2/3): 1-29. DOI: 10.1016/j.paerosci.2008.10.002.
[20]DANG T Q, KUMMER J D. Cross-flow fan propulsion system: U.S. Patent 7,641,144 [P]. 2010-1-5.
[21]朱雯雯. 轮式起降无人机全包线控制律设计技术研究[D]. 南京: 南京航空航天大学, 2012. ZHU Wenwen. Research on whole envelop control law design technology for automatic takeoff and landing UAV[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012.
[22]PAMADI B P. Performance, stability, dynamics, and control of airplanes [M]. Reston, VA: AIAA Educational Series, Reston, Virginia, 1998: 116-121. DOI:10.2514/4.862274.
[23]张明廉. 飞行控制系统[M]. 北京:国防工业出版社, 1984: 36-52. ZHANG Minglian. Flight control system[M]. Beijing: National Defence Industry Press, 1984: 36-52.
(编辑 张 红)
Take-off performance of the fan-wing aircraft
MENG Lin, YE Yongqiang
(School of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China)
To verify the short take-off and large-load characteristics of the fan-wing aircraft, a 6 kg fan-wing aircraft is studied. Based on the analysis of its structure characteristics and flight principle, the longitudinal model is built according to the force analysis on the ground and in the air, which effectively connects the ground running and the aerial flying. Meanwhile, four factors (elevator deflection, position of center of gravity, fan wing rotation speed, and airplane load) influenced the take-off running distance are analyzed and compared through numerical simulations. The simulation results show that: the no-load flight leads to the shortest take-off distance; the elevator deflection is located as large as it can be during the take-off process; as the center of gravity closer to the force application position of the cross-flow fan, the take-off distance remains shorter; when the factors are fixed, the shortest take-off distance, less than 9 m, is obtained with an optimal rotation speed. The allocation of the four factors is needed to gain a better take-off performance through the comparative analyses.
fan-wing aircraft; STOL; large-load; flight principle; longitudinal model
10.11918/j.issn.0367-6234.201602044
2016-02-27
孟 琳(1989—),女,博士研究生; 叶永强(1972—),男,教授,博士生导师
叶永强,melvinye@nuaa.edu.cn
V11
A
0367-6234(2017)04-0095-06

