基于粒计算的非常规突发事件情景层次模型
陈雪龙,卢 丹,代 鹏
(大连理工大学管理与经济学部,辽宁 大连 116024)
基于粒计算的非常规突发事件情景层次模型
陈雪龙,卢 丹,代 鹏
(大连理工大学管理与经济学部,辽宁 大连 116024)
针对已有非常规突发事件情景表示模型与构建方法在支持多层次用户过程中所表现出来的不足,本文首先给出情景要素的形式化表示;在此基础上,给出基于粒计算非常规突发事件情景层次模型;给出情景泛化算法,实现低层次情景到高层次情景的泛化过程;最后通过一个算例探讨模型的应用过程,并论证其科学性及可行性。研究结果表明,基于粒计算给出非常规突发事件情景层次模型,可有效实现基于复杂、不确定情景信息快速生成满足不同层次应急管理用户需求的不同粒度情景结构。
非常规突发事件;情景;情景层次模型;情景泛化;粒计算
1 引言
近年来,非常规突发事件频发,不但威胁到人民的生命安全,还对经济社会的发展造成了严重的损失[1]。较之传统的突发事件来说,非常规突发事件前兆缺失,发生和演变机理复杂,直接及次生、衍生危害严重,使得非常规突发事件具有“情景依赖”特性,其应急管理模式正在发生从“预测-应对”到“情景-应对”的重大演变[2-3]。
非常规突发事件的应急管理过程中,情景是决策者赖以决策的基础和依据。基于李仕明等[4]对非常规突发事件情景的阐述,本文认为非常规突发事件情景是在突发事件发生后,决策主体所正在面对的真实的境况,即任何能够表示非常规突发事件当前所含实体特征的信息。针对非常规突发事件情景的表示、构建及其演化,国内外的众多学者进行了深入的研究。Dettinger等[5]基于19世纪和20世纪的历史数据,以加利福尼亚为背景构建了一个极端的冬季风暴情景。Rivas-Medina等[6]在观测2011年洛尔卡地震数据的基础之上,构建了一个损毁情景模型,从而为相似程度的地震提供处理依据。吴广谋等[7]中认为某时刻的情景是各个情景要素在该时刻的状态信息,而且在状态信息的基础上提取了对当前的一个状态描述。仲秋雁等[8]通过情景元模型、情景概念模型以及情景概念模型的实例化来说明情景的构建过程。武旭鹏等[9]中对情景特征要素进行识别、区分及分类,并基于知识元模型完成对情景的规范化表示。刘奕等[10]针对突发事件案例分析问题提出了多维情景空间方法,以情景作为推演的基本单元,以要素作为情景表达的基本维度,建立多维空间坐标系统,从而将情景表达为多维情景空间中由若干个“点”构成的“轨迹”,实现对情景、情景相似度、情景推演的量化描述。刘德海等[11]将城市拆迁问题的演化博弈模型与不同对抗成本下的情景预设相结合,研究城市拆迁突发事件中地方政府和被拆迁户之间博弈冲突多种情景下各种演化结果。有的学者通过构建GRETS网络模型,判断情景走向的概率来实现情景推演,主要是在宏观上分析突发事件情景的发展,没有在细粒度上观察情景要素属性状态的变化[12-14]。Prakash等[15]基于光滑粒子流体动力学方法构建了洪水溃坝灾害情景模型,综合考虑坝体碎片、地形地势等影响因素对洪水溃坝情景的影响。Hu等[16]融合随机模型与多属性效用评估对城市洪涝灾害进行情景规划。上述2方法精确的描述了情景状态信息,为应急决策提供了较好支持,但却较依赖数据统计信息,适用于特定类型的突发事件。王循庆[17]构建了震后次生灾害预测随机Petri网模型,实现震后次生灾害演化情景的动态推演。该方法对事件情景进行了结构化描述及定量分析,但突发事件是多属性集合,基于属性关联的Petri网模型在描述突发事件时容易变得很庞大,难以直观进行应急决策分析,亦不宜即时构建。Li Jian等[18]构建了带有循环链的灾害因果关系演化网络模型,通过对灾害演化的动态分析,模拟了灾害情景的演变过程。但其缺乏对事件结构化的描述,影响模型适用性。
以上研究从形式化表示视角给出了非常规突发事件的情景模型和构建方法,并从演化的视角对情景的走向进行了预测或概率分析。然而,非常规突发事件的应急管理通常需要多层次用户的共同参与,高层决策者通常需要的是较为宏观的对事件态势总体情况的描述,而较低层次的用户通常需要更为具体的现场信息。因此,情景信息应有粒度粗细之分,相应的情景表示模型也应具有为不同层次用户提供不同粒度情景信息的能力,而现有研究均未从该视角审视非常规突发事件情景的表示与构建问题。
此外,由于非常规突发事件具有高度复杂、不确定的衍生及耦合等特性,其情景的表示与构建必然具有信息“过剩”(情景信息的多源、异构特性所致)、信息缺失及知识不完备(情景的复杂、不确定性所致)等特点,即其具有大数据处理特性。因此,当应用现有的理论、模型与方法构建面向多级用户支持的非常规突发事件情景表示模型时,仍将存在巨大挑战。
粒计算(Granular computing)是当前计算智能研究领域中模拟人类思维和解决复杂问题的新方法,广泛应用于不确定、不精确、不完整信息的处理,是知识获取与信息处理的有效工具[19-23]。粒计算通过简化对物理世界和虚拟世界的认识,可高效提供“实用”的非精确解,近年来已成为一种发展迅速的大数据处理范式[24]。澳门大学陈俊龙[25]更是将粒计算列为驾驭大数据的第一方法。通过构建情景的不同层次粒结构,可使应急管理用户在海量、不确定的情景信息中聚焦主要矛盾,降低事件处理的盲目性;辅以粒层间的相应计算,可得到适用于不同层次应急管理用户的不同粒度情景知识或信息。因此,本文在非常规突发事件情景要素形式化表示的基础上,基于粒计算相关理论给出非常规突发事件情景的层次模型,进而探讨低层次情景到高层次情景的泛化算法,从而实现基于基本的情景信息生成适用于不同层次应急管理用户的情景。
2 粒计算基础
粒计算是在解决问题过程中使用“粒度”的所有理论、方法、技术和工具的“标签”,其并不是具体的模型或方法,而是一种方法论[26],包含了如词计算、粗糙集、商空间、云模型、区间集、邻域系统等诸多具体模型。
粒计算的基本组成主要包括3部分[27]:粒子、粒层和粒结构。粒子可被同时看作是由内部属性描述的个体元素的集合,以及由它的外部属性所描述的整体。对粒子进行“量化”时用粒度来反映粒化的程度。按实际需求的粒化准则得到的所有粒子的全体构成一个粒层。粒层的内部结构是指在该粒层上的各个粒子组成的论域的结构,即粒子之间的相互关系。粒计算模型的主要目标是能够在不同粒层上进行问题求解,且不同粒层上的解能够相互转化。所有粒层之间的相互联系构成一个关系结构,称为粒结构。
粒计算中的2 个最基本问题为粒化和粒的计算[27]。粒化为在给定粒化准则下将问题空间中的个体聚集成不同粒子得到一个粒层的过程。粒的计算以粒子为运算对象进行问题的求解,包括同一粒层上粒子之间以及不同粒层上粒子之间的转换或推理。
对于粒的表示、粒层及粒结构的生成以及粒的计算等,粗糙集、商空间、云模型等粒计算具体模型均从各自视角给出了相应的算子及计算过程,篇幅所限,不再赘述。
基于上述粒计算的基本思想及过程,本文结合非常规突发事件情景的特性,给出情景粒、情景粒层及情景粒结构的表示及构建过程(即粒化);给出情景粒层的泛化算法,实现基于基本的情景信息生成不同粒度的情景粒层结构(即粒的计算),从而满足不同层次应急管理用户对不同粒度情景的需求。
3 情景要素的形式化表示
构建非常规突发事件的情景,必须建立在对事件系统相关事物及其相互作用关系的有效认知基础之上。将事件系统相关事物作为情景中的要素,可构成论域U,即情景要素的集合。论域U可表示如下:
U={u1,u2,…,un},n>0
∀i,j∈{1,2,…,n},ui≠uj
(1)
其中,ui为情景要素,是构成情景的不可再分或无需再分的基本单元。情景要素可从其属性及其属性间关系两方面进行刻画,形式化表示如下:
ui=(Ai,Ri),ui∈U
(2)
Ri⊆Ai×Ai,
(3)
a=(pa,da,fa),a∈Ai
(4)
(5)

4 基于粒计算的情景层次模型
基于论域U及情景要素的形式化表示,结合粒计算相关理论,可给出情景层次模型。
4.1 情景粒及情景粒层
定义1:情景粒。情景层次模型的基本构成要素称为情景粒,表示为
g=(Ag,Rg,Pg,Xg)
(6)
其中,Ag为情景粒的属性集,其元素的表示形式同式(4);Rg为Ag×Ag上的属性映射关系集,描述情景粒自身属性状态变化及相互作用关系,其元素的表示形式同式(5);Xg为该情景粒的构成元素集合;Pg为对情景粒的描述,是情景粒中所含信息的展现途径,由定义4及定义5予以具体刻画。
情景要素作为情景的基本单元,构成了最基本的情景粒。对于情景要素ui构成的情景粒gi(i∈{1,2,…,n}),有Agi=Ai,Rgi=Ri,Xgi={ui}={gi},|Xg|=1,即该情景粒由1个元素构成(|·|表示集合的基数)。所有的情景要素构成的情景粒的集合形成了情景的一个粒层,记为glk,k=1,表示粒层的层次。为便于后续探讨,现给出情景粒层的形式化定义。
定义2:情景粒层。情景粒层是由粒化程度相同的情景粒及其间关系构成,用以支持某一层次的用户。粒层glk表示为:
glk=(Gk,Rk)
(7)
其中,Gk={gi|i=1,2,…,n},为构成粒层glk的情景粒集合,n>0为构成glk的情景粒个数;Rk={ri|i=1,2,…,m},为粒层glk中所有情景粒属性集之间的多元关系集,描述情景粒之间的相互作用关系,可用于支持情景的演化分析;m≥0为情景粒属性集之间关系的个数。∀ri∈Rk,ri⊆Ag1×Ag2×…×Agn,具体表示形式同式(5)。

情景粒的构成元素通常具有相同或相似的特性,而情景粒之间的结构较为疏松,表现为不同情景粒之间的低耦合性及同一情景粒内部的高内聚性。依该原则给出如下定理。
定理1:情景粒层的情景粒集合构成了情景的一个划分。
证明:用数学归纳法予以证明。


上式中的函数getElementSet(Xgi)用于获取集合Xgi所含最终情景要素的集合,鉴于情景粒的构成方式,其可通过递归方式实现,篇幅所限,不再赘述。


综上,得证。
为刻画定义2中所述情景粒的粒化程度,给出情景粒层的粒化度的概念。
定义3:情景粒层的粒化度。用以表示情景在该粒层上的抽象程度,表示为:
(8)
由该定义及情景粒的构成方式可知,层次越低,情景粒层的粒化度越小,相应的情景抽象程度越低;反之,则越高。
定理2:0≤D(glk)<1。

定义4:描述。对于情景粒g的任意属性a∈Ag,v(a)表示a的取值,则称(a,v(a))为g一个描述,记作ρ,即ρ=(a,v(a))。若属性取值为空,则ρ=(a,null)。一般而言,情景粒需多个描述构成的描述集来表示。
定义5:描述集。情景粒g的多个描述构成的集合称为g的描述集,记为P,即P={ρ1,ρ2,…,ρm},m为情景粒g属性的个数,ρi=(ai,v(ai)),ai∈Ag。
4.2 基于情景粒层的情景层次模型
基于情景粒层粒化度的大小,可给出粒层间的偏序关系,进而构成多层次情景模型,形式化表示如下:
SC=(GL,RSC)
(9)

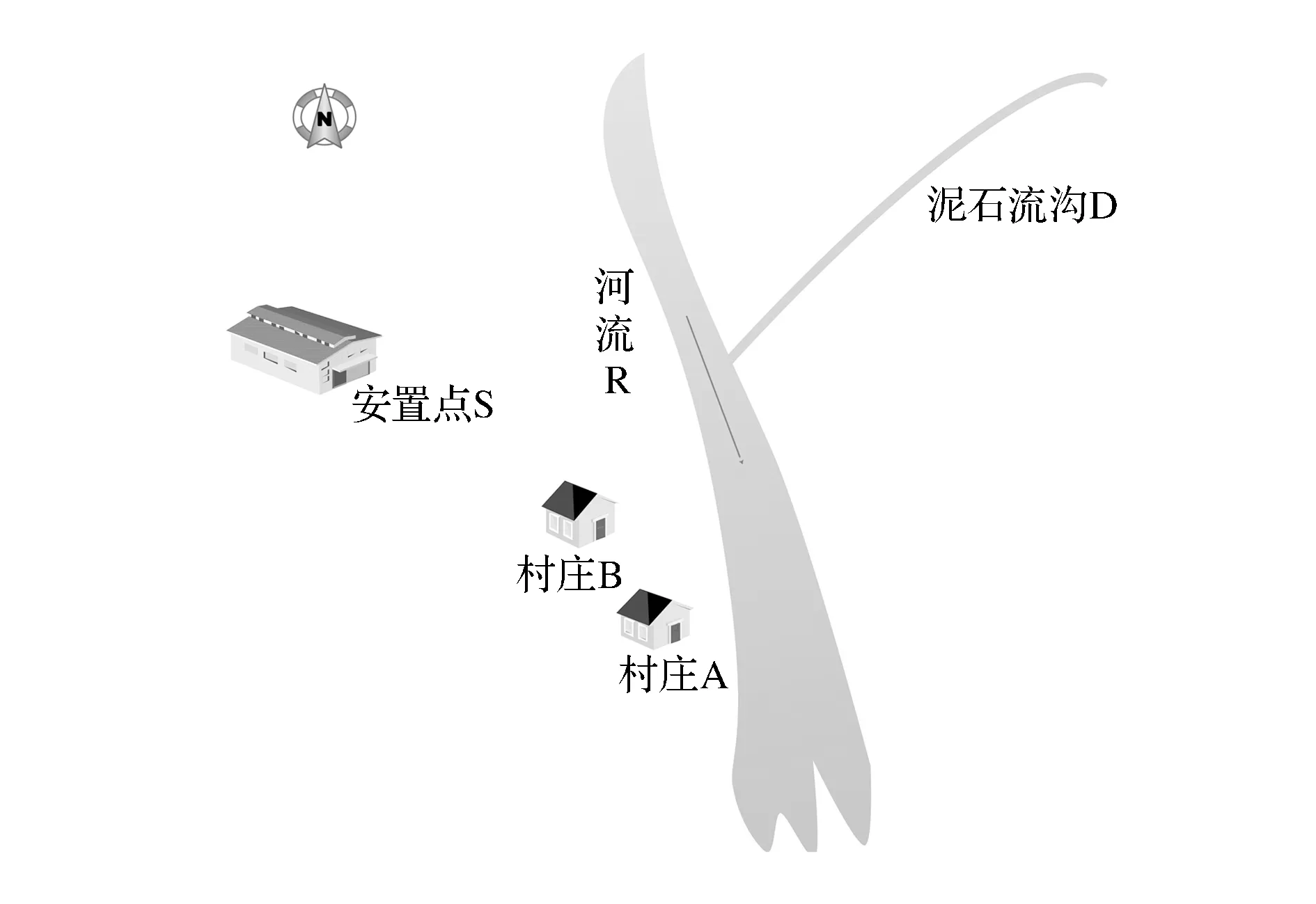
若有∀gli,gli+1∈GL,i∈{1,2,…,k-1},D(gli) (10) (11) (12) 至此,本节给出了情景层次模型的详细刻画,其形象示意如图1所示。如果说情景是突发事件的真实映像,情景层次模型则是对这种映像在不同粒度上的、纵向上的有机组合。较高层次的情景由粒度较粗的情景粒构成,更侧重在宏观层面上去刻画突发事件;而较低层次的情景粒度相对较细,更为适合刻画突发事件的细节信息。 非常规突发事件发生时,最易获得的情景信息通常是事件现场获得的细节信息,而较高层次的用户掌握的较为宏观的信息通常由细节信息综合、泛化、归纳而成。因此,本节基于前述对情景层次模型的探讨,给出情景粒层的泛化算法,从而实现基于基本的情景信息生成适合于不同层次应急管理用户的情景。 图1 情景层次模型示意图 情景泛化的本质是依据情景粒层间的层次结构及映射关系,基于最底层情景依次获得较高层次情景信息的过程。将情景层次模型及最底层的情景信息作为输入,经由泛化算法,输出多层次的情景信息,即 类C语言伪代码实现的泛化算法简要表示如下。 voidScenario-Generalization( ){ initHSC( ); //构建初始的情景层次结构;对任意的情景粒属性ai,有ρi=(ai,null) instantiateBottomGL(G1,P*);//实例化最底层情景粒,即为情景粒属性赋值 for(i=2;i<=k;i++){//生成情景粒层gli,k为情景粒层个数 for(s=1;s<=|Gi|;s++){//生成粒层gli的每一情景粒 for(s’=1;s’<=m;s′++){//对用于生成情景粒gs的映射集进行循环处理 flag=0;//设标志位 break; flag=1; //存在空值的属性,退出循环,置标志位 } } if(!flag) } } } } 算法中的关键变量命名同前述讨论;initHSC、instantiateBottomGL、executeComputation等函数的功能具有自明性,且易于实现,篇幅所限,不再赘述。 可以看出上述算法的核心是判断粒层间各映射的输入属性是否均被满足,若满足,则执行相应的映射运算,由较低层地的情景粒属性值计算得到相应相邻较高层次情景粒的属性值;较高层次的情景粒属性在获得具体属性值后,可进而通过相应的映射关系泛化得到其上一层次相应情景粒属性值。循环往复,直至获得最顶层情景粒的属性值,从而获得用于支持多级应急管理用户的多层次情景信息。由于情景要素间、情景粒间以及不同粒层间映射涵盖模糊、随机或概率映射,该算法可有效应用于复杂、不确定情景信息的泛化过程。 汶川地震是典型的非常规突发事件,其危害性不仅体现在地震本身,更体现在由地震引发的众多次生灾害上。2010年8月13日凌晨零点30分, 在持续强降雨作用下, 位于汶川地震重灾区的四川省绵竹市清平乡文家沟暴发特大泥石流灾害, 泥石流冲塌绵远河上游幸福大桥后, 将大桥整体推移到下游并堵塞老清平大桥,致使绵远河堵塞、水位抬高、河水改道[28]。事故发生后,清平乡应急部门立即组织相关村组进行转移,并将救援情况及泥石流事故数据上报市级应急部门,市级应急部门在专家组的协助下分析相关数据,做出决策,同时将相关情况上报省级应急部门。本文以该泥石流灾害及其应急处置过程为背景,从乡镇、市、省三个层次应急管理用户的视角出发,详细描述情景层次模型构建和具体的泛化过程,从而论证其有效性及科学性。 6.1 基本情景的描述 根据该泥石流灾害及应急救援的实际情况,给出如图2所示的情景简要示意。泥石流灾害M于泥石流沟D处引发,在沟口存在河流R,河流由北向南,在河流下游存在A和B两个村庄,河流上游存在一个安置点S。以该情景为依据,抽取相关要素,构成论域U,即 U={泥石流沟D,泥石流M,河流R,村庄A,村庄B,安置点S}。 各情景要素的主要属性如下[29-32]: A泥石流沟D={流域面积,主沟长度,主沟流域相对高差,主沟平均坡度,黏粒含量} A泥石流M={泥石流容重,泥石流流速,泥石流断面积} A河流R={河宽,河流流速,河流坡度,河流水深} A村庄A={人数,位置,平均海拔} A村庄B={人数,位置,平均海拔} A安置点S={帐篷数量,饮用水量,安置人数} 图2 泥石流灾害情景示意图 6.2 粒层的构建 表1 各粒层的情景粒集 6.3 粒层间映射的构建 依文献[29-32]给出如表3所示的粒层间映射关系集。 6.4 情景粒层的泛化过程 基于前述构建的粒层结构,应用第5节给出的粒层泛化算法,可实现基于粒层gl1信息递推获得粒层gl2及gl3信息的过程。粒层gl2及gl3中情景粒描述集中的属性值变化过程如表4所示。表中i、s及s’等变量的含义同算法Scenario-Generalization中的相应变量。 经过上述泛化过程,得到了G2、G3所含情景粒描述集中的非空属性值,如表5所示。结合表1、表2中有关gl2的信息,最终形成了面向乡镇、市、省三个层次应急管理用户的详细情景信息。 6.5 泛化结果分析 算例针对泥石流灾害,构建面向乡镇、市、省三个层次应急管理用户的情景粒层,并基于该粒层实现情景间的泛化算法。算例结果及分析如下: (1) 市级应急管理用户得到情景信息包括:帐篷需求量为162.5顶、水需求量为13000kg,而当前可用帐篷量和可用水量分别为150顶和10000kg。该结果表明当前物资短缺,应向上级申请相关物资的调配,并且应对现有应急物资进行合理的分配。此外,由泛化过程可得到泥石流流量、泥石流最大堆积宽度、河流流量等与泥石流灾害有关的重要信息,领域专家可据其对泥石流的发展态势进行分析,进而给出合理化建议。 表2 各粒层的情景粒相互作用关系集 表3 粒层间映射关系集 表4 情景粒层泛化过程 表5 高层次情景中情景粒集 (2) 省级应急管理用户得到的情景信息为:泥石流影响范围为0.3733km2,堵塞河道系数为6.385,物资紧缺。由文献[30]对泥石流影响范围的界定及A、B村距离沟口的位置(约300m)可知,泥石流可能对两村产生影响;另外,由于堵塞河道系数较大,泥石流很可能堵塞河道,上游水流聚集从而使河流向西改道,威胁到A、B村的安全。而在确定物资是否充足后,可针对物资调配问题进行相应的决策。 (3) 为简要说明问题,本算例抽取了泥石流灾害中的6个相关事物构成基本情景要素集,构建3个层次共10个情景粒的粒层结构,并对涉及到的17个映射关系进行详细描述,一定程度上验证了情景层次模型及情景层次泛化算法的有效性和科学性。由于本文给出的情景层次模型及相应的泛化算法并未对情景的类别与规模进行限定,因此,针对其他更加复杂的非常规突发事件,仍可应用本文的模型依据具体的需求设定合理的情景粒、粒层结构以及粒层间映射关系,并应用相应的算法实现情景的泛化。由于粒计算可在海量、不确定的情景信息中聚焦主要矛盾,一定程度上可在不影响推理计算质量的前提下降低情景的复杂性与不确定性,从而提升各类非常规突发事件情景泛化的效率。 非常规突发事件的应急管理通常需要多层次用户的共同参与,且情景是应急管理者赖以决策的依据。本文针对现有非常规突发事件情景表示与分析方法在支持多级应急管理用户方面表现出来的不足,首先探讨了情景要素的形式化表示;在此基础上,基于粒计算相关理论给出了非常规突发事件情景的层次模型;通过构建低层次情景到高层次情景的泛化算法,实现了基于基本的情景信息生成可用于支持不同层次应急管理用户的情景。文章的最后通过一个算例验证了模型及方法的科学性及可行性。鉴于粒计算在大数据以及复杂、不确定性信息处理方面的优势,本文给出的模型可有效实现基于复杂、不确定情景信息快速生成满足不同层次应急管理用户需求的不同粒度情景结构。 由于本文给出的情景层次模型及相应的泛化算法并未对情景的类别与规模进行限定,因此,对于其他更加复杂的非常规突发事件仍具一定的适用性。此外,情景层次模型及相应泛化算法的科学性依赖于粒层结构的合理性,包括情景粒的构成及粒层间映射的设定。因此,在模型的具体应用过程中,有效识别各级应急管理用户的实际需求并获取相对完备的底层基本的情景信息,是合理划分情景的层次、清晰界定情景粒的构成元素及属性集合、科学设定相邻粒层间情景粒的映射关系的前提,也是本文模型及方法有效应用的必要条件。 本文给出的情景层次模型及相应的泛化算法解决了由底层基本情景信息生成较高层次情景信息的问题。然而,非常规突发事件的“情景应对”除了上述自下而上(Zoom-out)的情景信息搜集过程以外,还需要自上而下(Zoom-in)的应急处置指导过程,即将高层决策信息传递至底层决策方案实施层面的过程。这本质上是一个情景细化的过程。因此,非常规突发事件情景层次模型的细化机制及方法将是笔者后续的重点研究内容。 [1] 钟永光,毛中根,翁文国,等.非常规突发事件应急管理研究进展[J].系统工程理论与实践,2012,32(5):911-917. [2] 华国伟,余乐安,汪寿阳.非常规突发事件特征刻画与应急决策研究[J].电子科学大学学报(社科版),2011,13(2):33-36. [3] 李仕明,刘娟娟,王博.基于情景的非常规突发事件应急管理研究 ——“2009突发事件应急管理论坛”综述[J].电子科技大学学报(社科版),2010,12(1):1-3. [4] 李仕明,张志英,刘樑,等.非常规突发事件情景概念研究[J].电子科技大学学报(社科版),2014,16(1):1-5. [5]Dettinger M D, Ralph F M, Hughes M, et al. Design and quantification of an extreme winter storm scenario for emergency preparedness and planning exercises in California[J]. Natural Hazards, 2012, 60(3): 1085-1111. [6] Rivas-Medina A, Martínez-Cuevas S, Quirós L E, et al. Models for reproducing the damage scenario of the Lorca earthquake[J]. Bulletin of Earthquake Engineering,2014,12(5): 2075-2093. [7] 吴广谋, 赵伟川, 江亿平.城市重特大事故情景再现与态势推演决策模型研究[J].东南大学学报(哲学社会科学版),2011,13(1):18-23. [8] 仲秋雁,郭艳敏,王宁,等.基于知识元的非常规突发事件情景模型研究[J].情报科学,2012,30(1):115-120. [9] 武旭鹏,夏登友,李健行.非常规突发事件情景描述方法研究[J].中国安全科学学报,2014,24(4):159-165. [10] 钱静,刘奕,刘呈,等.案例分析的多维情景空间方法及其在情景推演中的应用[J].系统工程理论与实践,2015,35(10):2588-2595. [11] 刘德海,韩呈军,尹丽娟.城市拆迁群体性事件演化机理的多情景演化博弈分析[J].运筹与管理,2016,25(1):76-84. [12] 方志耕,杨保华,陆志鹏,等.基于Bayes推理的灾害演化GERT网络模型研究[J].中国管理科学,2009,17(2):102-107. [13] 杨保华,方志耕,刘思峰,等.基于GERTS网络的非常规突发事件情景推演共力耦合模型[J].系统工程理论与实践,2012,32(5):963-967. [14] 周愉峰,马祖军. 基于情景推演的地震灾害演化动态GERT 网络模型[J]. 自然灾害学报,2012,22(3):68-75. [15] Prakash M, Kai R, Cleary P W. Modelling the impact of dam failure scenarios on flood inundation using SPH[J]. Applied Mathematical Modelling, 2014, 38(23):5515-5534. [16] Hu Shaolong, Han Chuanfeng, Meng Lingpeng. A scenario planning approach for propositioning rescue centers for urban waterlog disasters[J]. Computers & Industrial Engineering, 2015, 87:425-435. [17] 王循庆. 基于随机Petri网的震后次生灾害预测与应急决策研究[J]. 中国管理科学, 2014,22(11):159-165. [18] Li Jian, Chen Changkun. Modeling the dynamics of disaster evolution along causality networks with cycle chains[J]. Physica A: Statistical Mechanics & Its Applications, 2014, 401:251-264. [19] Yao Yiyu. Granular computing: Basic issues and possible solutions[C]//Proceedings of the 5th Joint Conference on Information Sciences. 2000, 1: 186-189. [20] Skowron A, Stepaniuk J. Information granules: Towards foundations of granular computing[J]. International Journal of Intelligent Systems, 2001, 16(1): 57-85. [21] Chen Guang, Zhong Ning, Yao Yiyu. A hypergraph model of granular computing[C]//Proceedings of the 2008. IEEE International Conference on. Granlar Computing,August 26-28, 2008: 130-135. [22] Bargiela A, Pedrycz W. Toward a theory of granular computing for human-centered information processing[J]. IEEE Transactions on Fuzzy Systems, 2008, 16(2): 320-330. [23] Yao Yiyu. Interpreting concept learning in cognitive informatics and granular computing[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B(Cybernetics), 2009, 39(4): 855-866. [24] 徐计,王国胤,于洪.基于粒计算的大数据处理[J].计算机学报,2015,38(8):1497-1517. [25] Chen C L P, Zhang Chunyang. Data-intensive applications, challenges, techniques and technologies: A survey on big data[J]. Information Sciences, 2014,275:314-347. [26] 苗夺谦,李德毅,姚一豫,等.不确定性与粒计算[M].北京:科学出版社,2011. [27] 王国胤,张清华,胡军.粒计算研究综述[J].智能系统学报,2007,2(6):8-26. [28] 余斌,马煜,吴雨夫.汶川地震后四川省绵竹市清平乡文家沟泥石流灾害调查研究[J].工程地质学报, 2010, 18(6): 827-836. [29] 马欢,张绍和,刘卡伟.泥石流运动参数的计算方法[J].西部探矿工程,2010,22(6): 122-125. [30] 刘希林,唐川,朱静,等.泥石流危险范围的流域背景预测法[J].自然灾害学报,1992,1(3): 56-67. [31] 张金山,谢洪.岷江上游泥石流堵河可能性的经验公式判别[J].长江流域资源与环境,2008, 17(4): 651-655. [32] 聂高众,高建国,苏桂武,等.地震应急救助需求的模型化处理[J].资源科学,2001,23(1): 69-76. Hierarchical Scenario Model of Unconventional Emergency Based on Granular Computing CHEN Xue-long,LU Dan,DAI Peng (Faculty of Management and Economics,Dalian University of Technology,Dalian 116024,China) To cover the shortages of existent scenario representation models and scenario construction methods for unconventional emergency in being used to support multi-level emergency management personnel, the formal representation of scenario elements is discussed firstly. Then, the hierarchical scenario model of unconventional emergency based on granular computing is proposed. Afterwards, the scenario generalization algorithm is put forward to realize the scenario generalization processes from low-level scenarios to up-level scenarios. In the end, an example is analyzed to illustrate the application process and to prove the scientificalness and the feasibility of the proposed model. The results show that the hierarchical scenario model of unconventional emergency based on granular computing can generate scenario structures of different granularities which can be used to support multi-level emergency management personnel on the basis of complex and uncertain scenario information. unconventional emergency; scenario; hierarchical scenario model; scenario generalization; granular computing 1003-207(2017)01-0129-10 10.16381/j.cnki.issn1003-207x.2017.01.014 2015-08-28; 2016-06-02 国家自然科学基金资助项目(71203019,71533001);辽宁省社科规划基金资助项目(L13DGL061);辽宁经济社会发展立项课题(2016lslktziglx-05);国土资源部黄土地质灾害重点实验室开放基金(KLGLAMLR201602) 陈雪龙(1978-),男(汉族),吉林白山人,大连理工大学管理与经济学部,博士,副教授,研究方向:应急管理与知识管理,E-mail:chenxl_dg@dlut.edu.cn. X913.4 A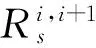

5 情景粒层的泛化算法






6 算例分析




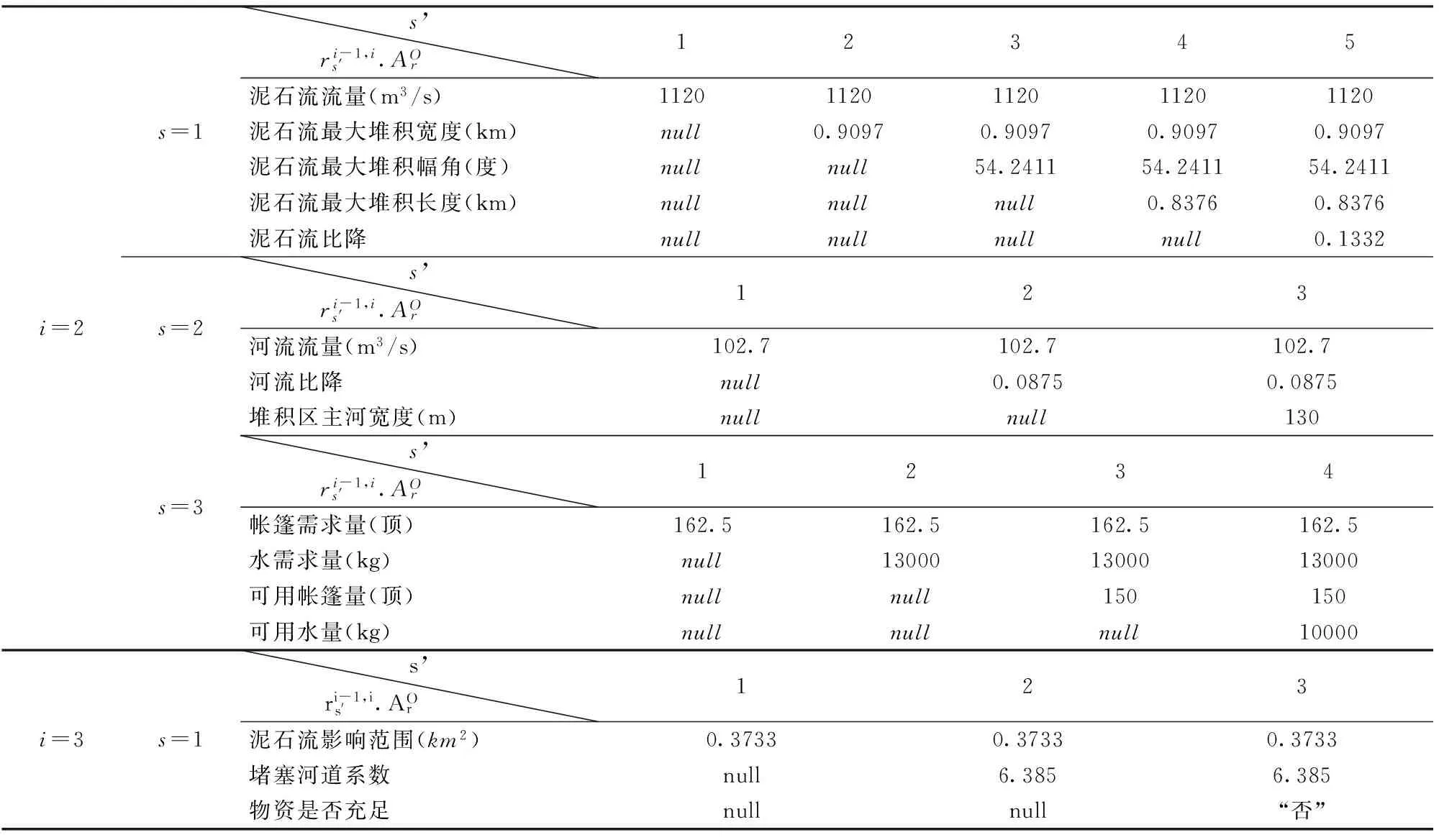

7 结语

