蚁群算法中的主要参数对任务分配问题影响的分析

沈阳理工大学自动化与电气工程学院 伊文康 曹 帅

蚁群算法中的主要参数对任务分配问题影响的分析

沈阳理工大学自动化与电气工程学院 伊文康 曹 帅

该文主要针对多机器人的任务分配问题，对蚁群算法的主要参数进行介绍和分析。首先对蚁群算法进行介绍，并对蚁群算法中的参数进行分析和选择，最后根据选定的参数对算法进行仿真验证。

蚁群算法；数学模型；任务分配

蚂蚁可以说是人类最常见、数量最庞大的昆虫之一，它们常常成群结队地出现在人类的日常生活环境中。这些昆虫群体生物智能方面的特征，于是引起了一些学者的注意。意大利学者M.Dorigo，V.Maniezzo等人在观察蚂蚁的觅食习性时发现，蚂蚁总能找到巢穴与食物源之间的最短路径。经研究发现，蚂蚁的这种群体协作功能是通过一种遗留在其来往路径上的叫做”信息素”的挥发性化学物质来进行通信和协调的。通过对蚂蚁觅食行为的研究，他们发现，整个蚁群就是通过这种信息素进行相互协作，形成正反馈，从而使多个路径上的蚂蚁都逐渐聚集到最短的那条路径上。

1.蚁群算法原理

根据前面的蚂蚁留下的分泌物，蚂蚁会选择相应的路径[21]。在该路径上放电的强度越大相应的蚂蚁选择这条路径的概率也就越大。因此，这种集体行为可以理解为一种正反馈现象，即由蚂蚁群体构成的一种积极的学习信息的反馈现象：后面的蚂蚁是否选择某一条路径取决于在这条路上走过的蚂蚁数量，数量越大，后面蚂蚁选择该条路径的概率越大。蚂蚁就是这样选择最短路径的。

蚁群算法通过将蚂蚁觅食行为转化为一种优化算法再用来求解最优解[22]。这样的方法与一般的编程模式不同，有自己的明显优点，可以在一定程度上减少程序的代码量，而算法本身通过事先设定好的规则迭代寻找问题的最优解。代表的含义就是如果算法在最开始寻找到的目标一般情况下都不是最优的解决策略，而且也很有可能带有不正确的决策策略。但通过算法的进行，利用蚂蚁觅食过程中释放的信息素，不断接近最优路径，即解决问题的最短路径，这就意味着，随着程序的不断执行，决策的最优路径与问题的最优路径逐渐接近。这似乎看起来像我们数学中学的归纳概括方法一个具体应用。程序本身在运行的同时也在不断的进行学习[23]。

通过模仿蚂蚁的行为，蚁群算法实现优化。但是该算法不同于传统的编程模型，它的优点是明显的，即为了避免长的编程和规划，程序本身是基于一定的规则来找到随机运行的最佳解决方案[24]。也就是说，如果在一个计划中在一开始便找到目标，那么它的路径几乎不可能是最优的路径，甚至可能包含无数的错误选择和非常冗长的过程。然而，可以通过在程序中采用蚂蚁搜索食物时的信息素的原则，继续修改原来的路线，也就是说，若程序执行时间较长，路径更接近最优的路径。这看起来像是很多的例子总结而形成的最佳路径。然而事实上，它是一个自我学习的过程[25]。

2.蚁群算法的参数分析

2.1 蚁群数目m

通常情况下人们可能普遍认为蚁群数目越大相应的搜索速度越快，但并非如此。初始蚂蚁的数目m越大，相应的蚁群算法在全局的收敛性就会越强，但当蚂蚁数目m达到一定程度后，会发现之前蚂蚁留下的信息素在搜索过程中变化不明显，会影响接下来蚂蚁的判断会走很多弯路影响蚁群算法的收敛速度，但蚂蚁数目m也不能过小，m过小意味着算法的全局搜索性减弱，收敛速度过快，可能造成蚁群算法稳定性降低。所以要根据实际问题选择合适的数目m。

2.2 挥发系数ρ

挥发系数ρ直接影响蚁群算法的全局搜索能力和收敛速度[31]；各个蚂蚁之间的相互影响作用可以用（1-ρ）代表的剩余信息素表示，其值越大信息更新的效率就会受到影响，进而算法的收敛速度相应减慢；其值越小搜索的多样性减少，可能导致陷入局部最优值，算法收敛速度过快[32]。

2.3 启发因子α

α代表某个蚂蚁在某个经过的路径上留下的信息素被重视的程度。其值越大对蚂蚁选择这条路径的影响就越大，但减少了选择的多样性。其值低，容易导致陷入局部最优。

2.4 启发因子β

启发因子β称为期望启发因子，代表蚂蚁遗留下来的启发信息的重要程度，β越大，蚂蚁选择离它近的城市概率越大就是找到局部最优路径的概率越大，加快了收敛速度，但选择多样性减少。

3.蚁群算法的求解步骤

基本蚁群算法主要有以下几个步骤：

（2）初始化位置：输入机器人初始位置坐标；

（6）根据公式计算选择任务j的转移概率；

（7）移动机器人到转移概率最大的点，并记录到禁忌表中；

（8）如果没有访问所有城市，跳转到（5），反之，转至（9）；

（9）更新信息素；

（10）判断是否满足终止条件，若满足输出结果，否则清空禁忌表并转到（4）。

蚁群算法的流程图如图1所示：

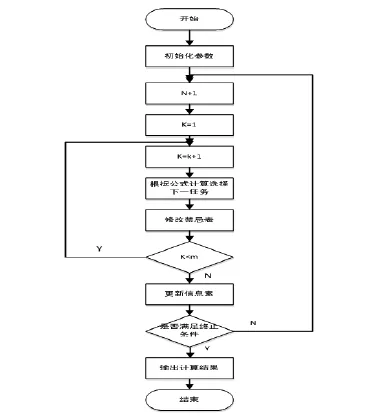
图1

4.基于蚁群算法的Matlab仿真

设定静止目标数量为4个，坐标分别位于（3，4），（9，8），（11，13）和（16，17）。可执行任务的AUV数量为4个，坐标分别位于（1，1），（2，2），（10，10）和（120，12）。蚂蚁数量m=10，启发因子α=1，启发因子β=5，挥发系数ρ=0.6，释放的信息素的总量Q=100，最大循环次数Nc max=200。

设置参数完成后，进行Matlab仿真，通过多次仿真，最好仿真结果如图2所示：

图2

仿真的结果显示，最好情况下，第一个机器人执行第一个和第二个任务，第二个机器人执行第三个任务，第四个机器人执行第四个任务。但不是每次都能得到最优情况，且即使两次结果都取到最优值时，所经过的路程也不同。