股指期货对股票现货市场波动性影响分析

高健多

摘 要：采用事件研究法，构造GARCH（1，1）模型，基于长期数据的基础针对沪深300股指期货的推出对现货市场波动性的影响进行实证研究。经过实证分析得到结论，从长期看来，沪深300股指期货的推出在很小程度上减弱了现货市场股票价格的波动性，但沪深300股指期货的推出却提高了现货市场对于新旧信息的反应效率。

关键词：股指期货；股票价格波动性；GARCH模型

中图分类号：F83 文献标识码：A doi：10.19311/j.cnki.1672-3198.2016.33.107

1 引言

中国首批沪深300股票指数期货合约于2010年4月16日在中国金融期货交易所正式挂牌交易。随着我国资本市场不断发展与完善，股指期货在当今证券市场中已起着重要的作用，可以满足各种投资者规避风险，套期保值，投机获利等不同的投资需求。但由于股指期货与生俱来的灵活性和大幅度的波动性，在股票价格的剧烈波动的问题上股指期货总是难辞其咎。沪深300股指期货的存在是否对股票现货市场价格的波动性产生影响，二者之间到底存在什么关系，这些问题从沪深300股指期货诞生之日起至今都是金融界讨论的热点话题。国内外学者针对这一问题进行过系统的分析，但各位学者得出的结论并不一致，具体体现为两方面对立的观点：

一方认为，因为股指期货具有价格发现、避险功能，可以提高市场的定价效率、实行反向操作以进行套期保值，从而间接地达到稳定市场、减少现货市场股票价格的波动率的效果。另一方则认为，在股指期货合约到期日当天，无论是股指期货市场的成交量，还是股票现货市场的成交量，都很可能会成倍急剧地放大，股票市场易发生剧烈震荡。

这场争论到现在都没有结束，双方都无法找到能说服对方的充足证据。本文应用GARCH模型，用虚拟变量来刻画股指期货推出事件，以对数化的沪深300指数日收益率序列作为研究对象，进行实证分析，通过科学严谨的数据分析来为这场争论寻找一个答案。

2 股指期货对股票价格波动的影响分析

2.1 数据选取及处理

本文选取了沪深300股票价格指数从2006年4月17日到2014年12月31日的日收盘指数。对于四种期货交易合约，本文选取沪深300股指期货当月合约从2010年4月16日到2014年12月31日的日收盘价格。

本文以沪深300股指期货正式推出时间，即2010年4月16日为界，将股指研究数据总样本分为前后两个对称阶段，以分析股指期货推出后对现货市场的长期影响。选取2006年4月17日到2010年4月15日沪深300指数日收盘指数数据为第一阶段，共计975个数据；第二阶段为2010年4月16日到2014年4月18日，共计980个数据。数据来源于Resset数据库、中国金融期货交易所、数优期货行情（含高频）数据库。

现代金融理论中通用收益率的标准差或方差来代表股票的波动率。为了消除金融时间序列的非平稳性，同时保证收益率序列的平稳性，本文运用E-views6.0软件采用对数差分的方法对研究数据进行处理。

对沪深300指数的日收益率序列进行统计性描述，发现其具有尖峰、左偏、厚尾的特征，不服从正态分布。对其进行ADF单位根检验，结果中其P值均趋向于0，在1%的显著性水平下，ADF值小于临界值，所以我们有理由相信该序列是平稳的。

2.2 识别收益率模型、选择滞后阶数

通过对股指期货推出前和推出后的沪深300指数的日对数收益率序列分别进行自相关检验。检验得到其自相关图，由图可知该序列存在自相关性，进一步可用ARMA模型来描述其动态路径。根据AIC和SC準则选择模型阶数后，对其残差进行自相关性检验。

通过AIC准则和SC准则选择出模型的滞后阶数。股指期货推出前沪深300指数的日对数收益率服从ARMA（2，2）模型，而股指期货推出后则服从于ARMA（1，1）模型。这说明股指期货推出后提高了现货市场对新、旧信息的反应效率，标志着信息传递效率的提高。

建立GARCH族模型的前提条件需要做ARCH效应检验，于是本文分别对股指期货推出前、后的收益率序列实施ARCH.LM检验。检验结果为：ARCH.LM的P值（0.01%、2.79%）趋向于0，在滞后阶数为20、5%的显著性水平下结果仍然显著。故拒绝原假设，认为股指期货推出前后残差序列均存在高阶ARCH效应，据此建立GARCH模型来进行估计。

2.3 建立GARCH（1，1）模型

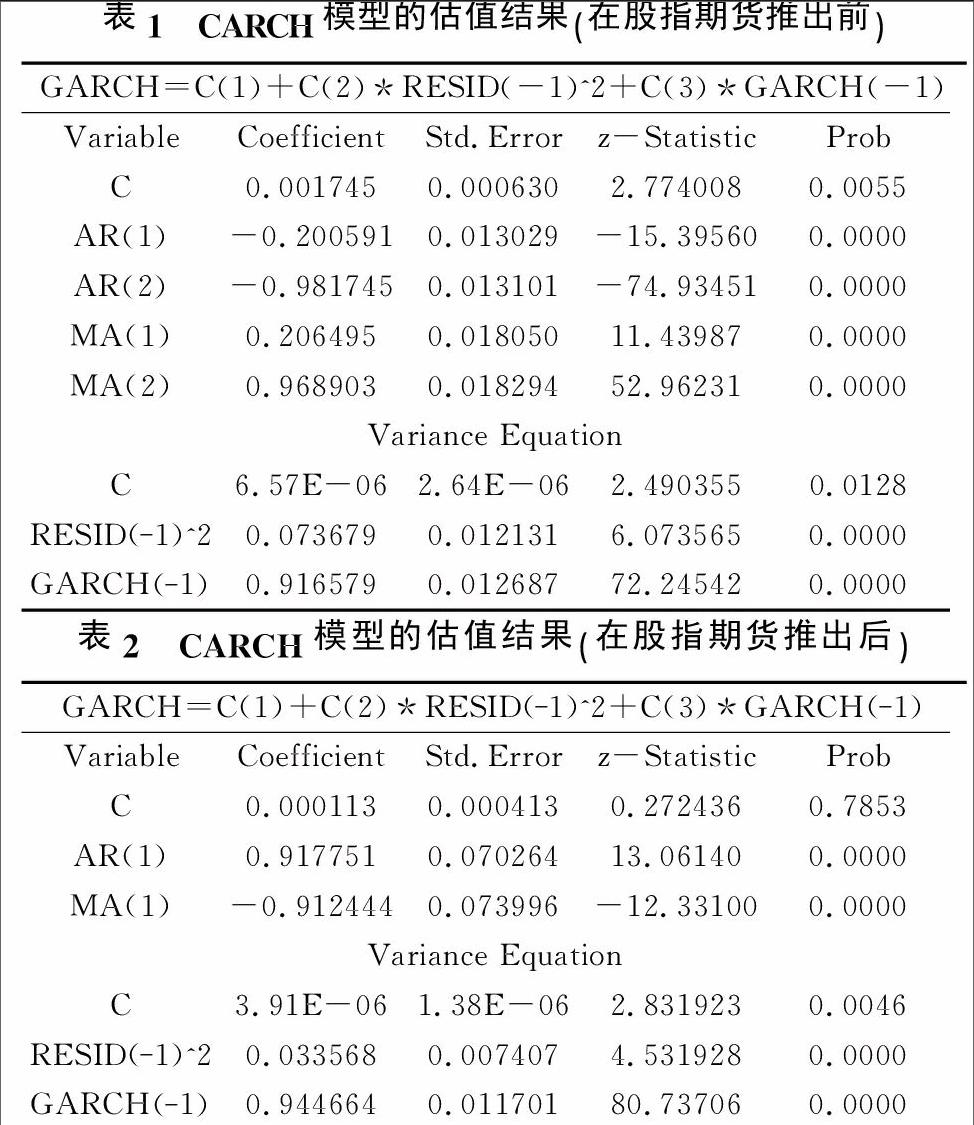
GARCH（1，1）模型被多数知名学者公认为非常适用于构建金融时间序列模型。于是，本文选取GARCH（1，1）模型分别对股指期货推出前后的沪深300指数日收益率进行估计，结果见表1和表2。

虽然表2中的常数项系数统计不显著，但出于计量经济学的视角，本文仍予以保留。

由表1和表2可知，所有变量的系数均统计显著，且估计系数之和小于1，满足平稳性条件。

最后再进行ARCH.LM检验。检验结果中的P值（79%、29%）均远大于5%，我们没有理由拒绝原假设。通过GARCH（1，1）模型估计后，原序列的ARCH效应已经消除。

2.4 引入虚拟变量的实证分析

为了刻画沪深300股指期货合约推出事件而引入一个虚拟变量DV，且DV的取值为0或者1。这样本文根据虚拟变量DV值就可以判断股指期货推出后现货市场价格波动率变化的情况。回归结果中对于DV值的分析主要有以下三点：DV的符号、DV的绝对值、DV的P值。

引入DV之后，GARCH模型的条件方差为：

σ2t=α0+α1μ2t-1+λDV

其中，股指期货推出之前DV=0，股指期货推出之后DV=1。

由前所述可知沪深300指数的日收益率总样本序列是平稳的、自相关的，因此可用ARMA模型来解释沪深300指数日收益率的变化。利用AIC和SC准则发现其对数收益率服从ARMA（2，2）模型。

又该总样本序列的ARCH.LM统计量的P值趋于0，且当滞后阶数为20时，回归结果仍然显著，说明总样本序列存在高阶ARCH效应，于是应建立GARCH模型。

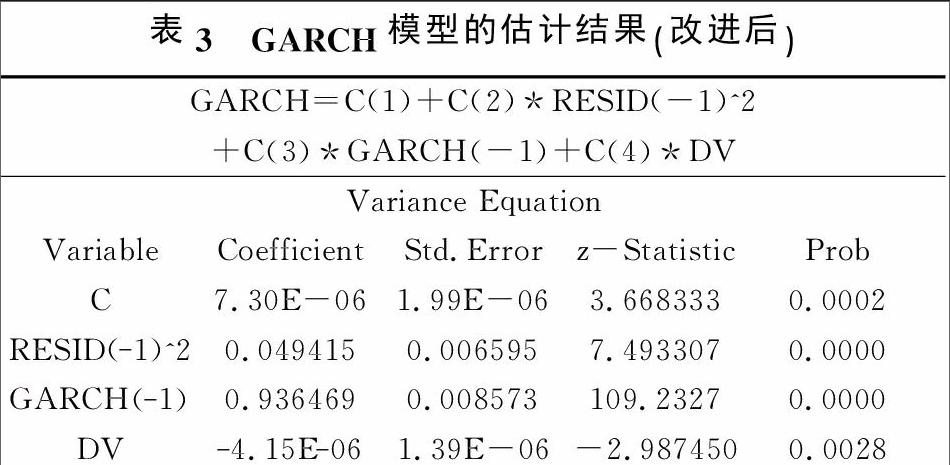
建立加入虚拟变量DV的GARCH模型，回归结果见表3。

DV的P值为0.0028，小于0.05，说明沪深300股指期货的推出对股票市场的波动性产生了显著影响。又DV的值很小且为负数，表明沪深300股指期货的推出在很小程度上减弱了现货市场股票价格的波动性，但却提高了现货市场对于新旧信息的反应效率。

3 结论

本文借助ARCH模型思想，并引入虚拟变量DV来刻画沪深300股指期货合约推出事件，利用GARCH模型进行实证分析。模型的回归结果中DV的值很小且为负数，所以实证分析结果表明沪深300股指期货的推出在很小幅度上减弱了股票价格的波动性。此外，通过事件发生前后对比分析，沪深300指数日收益率的时间序列由推出前的ARMA（2，2）过程变为ARMA（1，1）过程。这说明股指期货推出以后，新、旧信息对股票现货市场的影响均加快，也就是说信息传递的效率得到增加。