一种新型船模水动力性能测试装置研究
阳 航,涂海文,谢文雄,孙江龙,
(1. 华中科技大学 船舶与海洋工程学院,湖北 武汉 430074;2. 船舶和海洋工程水动力湖北省重点实验室,湖北 武汉 430074;3. 高新船舶与深海开发装备协同创新中心,上海 200240)
一种新型船模水动力性能测试装置研究
阳 航1,涂海文1,谢文雄1,孙江龙1,2,3
(1. 华中科技大学 船舶与海洋工程学院,湖北 武汉 430074;2. 船舶和海洋工程水动力湖北省重点实验室,湖北 武汉 430074;3. 高新船舶与深海开发装备协同创新中心,上海 200240)
目前,国内外的船模水动力性能测试装置均为平面运动机构,使得船舶水动力导数的测量范围有限,而一种新型船模水动力性能测试装置,即六自由度船模水动力性能测试装置可以扩大这一测量范围。从六自由度平台的工作原理,六分力天平量程的确定和测试装置总体设计 3 个方面来具体研究和设计六自由度船模水动力性能测试装置。首先具体介绍六自由度平台的工作原理,即平台 6 根运动杆的运动与船舶六自由度运动的对应关系;然后建立船舶六自由度运动所受力和力矩的初步计算公式,以国内外平面运动机构的具体技术性能指标为依据,确定试验装置中的六分力天平的量程;最后确定测验装置的整体设计,设计出现有船池拖车平台的具体形状与尺寸。以此为依据,综合考虑拖车平台的受力情况及拖车架和六自由度平台的安装方式,确定拖车架的具体结构形式与尺寸大小,得到三维示意图、二维安装图与尺寸图,进行结构强度分析。
六自由度;测试装置;六分力天平
0 引 言
六自由度运动机构的结构形式由 Stewart.D[1]于1965 年提出,洪鸣等[2]对六自由度运动平台的控制系统进行了详细分析,苏玉鑫等[3]对六自由度 Stewart 平台的运动精度进行了分析,王勇亮等[4]对位移传感器在六自由度运动平台中的应用进行了介绍,何景峰等[5]分析了六自由度平台的冲击响应,荣辉等[6]对六自由度平台的灵敏度进行了分析,杨达毅和陈丽敏[7]利用SolidWorks 软件对六自由度液压平台进行运动仿真。经过半个世纪的发展,六自由度运动机构本身的技术已经较为成熟,但其运用范围却有限。仅有飞行模拟器和六自由度机器人的实用度较大。而在船舶水池试验装置领域,国内外的研究主要集中在平面运动机构上,对六自由度运动机构却鲜有研究,从而限制了船舶水池试验的范围。将六自由度运动机构和船舶的六自由度约束运动相结合,可以得到一种六自由度船舶水池试验装置,对船舶领域科研的发展具有重要意义。
1 六自由度平台的工作原理
六自由度平台的功能具体体现在平台运动平台 6个自由度的运动上,该运动由 6 根运动杆的线性运动复合而成,包括 3 个位移和 3 个运动。这 6 个自由度的运动与船舶 6 个自由度的运动,即横摇、纵摇、首摇、横荡、纵荡和垂荡、从本质上来说是一样的。总的来说,要想让试验装置带动船模按照预定的横摇角、纵摇角、首摇角、横荡位移、纵荡位移和垂荡位移值来运动,就必须给六自由度平台所有运动杆以运动指令,即输入 6 个线性位移量,经过转换后输出为船舶的横摇、纵摇、首摇、横荡、纵荡和垂荡。本小节所论述的六自由度平台的工作原理正是 6 个线性位移量和横摇、纵摇、首摇、横荡、纵荡及垂荡的转换关系。为方便起见,将船舶及六自由度平台的 6 个运动量设为纵向位移 x,横向位移 y,垂向位移 z,横摇角 φ,纵摇角 θ 和首摇角 ψ。
考虑到六自由度平台结构的空间性,应该建立空间直角坐标系。又由于六自由度平台同时拥有固定平面和运动平面,所以应该建立 2 个空间直角坐标系,即固定坐标系和运动坐标系,分别设为 XBYBZB和XPYPZP。设固定平台的 6 个连接点为 Bi(i = 1,2,3,4,5,6),运动平台的连接点为 Pi(i = 1,2,3,4,5,6)。所建立的六自由度平台数学模型如图 1 所示。
2 个空间直角坐标系的坐标原点分别取为六自由度平台固定平面和运动平面的形心。这样,在知道六自由度平台具体结构尺寸的情况下,各连接点在各自坐标系下的坐标已知。将固定平面连接点 Bi在固定坐标系下的坐标表示为(Bix,Biy,0);将运动平面连接点 Pi在运动坐标系下的坐标表示为(Pix,Piy,0)(i = 1,2,3,4,5,6)。显然,运动坐标系的原点 OP相对于固定坐标系的坐标即为(x,y,z)。令向量
运动坐标系到固定坐标系的坐标转换矩阵[8]:
则运动平面的连接点 Pi相对于固定坐标系的坐标可表示为:
将方程(2)和方程(4)代入方程(1)中,可得:那么六自由度平台第 i 根运动杆的长度:
上述的数学推导实际上是对六自由度平台的运动学反解,即已知六自由度平台运动平面的 6 个运动量,求解六自由度平台 6 根运动杆杆长的变化。方程(6)建立了六自由度平台 6 根运动杆的运动与船舶 6 个自由度运动的对应关系。而在试验装置中则具体表现为,为了模拟试验船模的一个定量的六自由度运动,将已知的船模纵向位移 x,横向位移 y,垂向位移 z,横摇角 φ,纵摇角 θ 和首摇角 ψ 代入方程(6)即可求出六自由度平台各运动杆的杆长变化,将杆长的变化值作为指令传输给六自由度平台,六自由度平台便能带动试验船模做相应的六自由度运动,具体的指令传输程序将在以后做深入研究。而考虑到六自由度平台本身的运动精度有限,可以在六自由度平台上加装位移和转动传感器,将实际的 6 个运动量反馈给控制系统。
2 六分力天平量程的确定
六分力天平又叫做六分力传感器,美国的 P.CWatsno 于 1975 年设计了一种拥有 3 个垂直筋结构的六分力传感器[9]。六分力天平在试验装置中所起到的作用实际上是测量试验船模在水池作六自由度运动的过程中所受的 3 个力和 3 个力矩,将测量值作为已知量代入相关公式求解水动力导数。要想确定六分力天平的量程,必须估算出试验船模在作六自由度运动过程中所受到的力和力矩的最大值。船模在作六自由度运动时,影响其所受力和力矩大小的因素有很多,如船模自身的结构形状、船模的运动参数、船模的附加质量和附加惯性矩、波浪的影响及耦合影响等等。按照MMG 分离建模的基本思想,列出船模作六自由度运动过程中的运动方程[10]:
式中:上标 X,Y,Z,K,M,N 分别为船模所受纵向力、横向力、垂向力、横摇力矩、纵摇力矩和首摇力矩;下标 H,P,R,W 分别表示裸船体、螺旋桨、舵和波浪;m 为试验船模的质量;xG为船模重心的坐标值;mx,my,mz为船模在 3 个位移方向上的附加质量;u,v,w 为船模在 3 个位移方向上的速度;,,为船模在 3 个位移方向上的加速度;p,q,r 为船模在 3 个旋转方向上的角速度;,,为船模在 3 个旋转方向上的角加速度;Ix、Iy、Iz为船模对 3个坐标轴的面积惯性矩,Jx,Jy,Jz为相应的附加惯性矩。
由式(1)~式(6)可知,在已知试验船模具体尺寸、质量、重心坐标和各运动参数的条件下,可以估算出其作 6 自由度运动所受力和力矩。而为了估算这些力和力矩的最大值,方程右边所有已知参数都应该选取最大值。以 36 m 快艇为例,其宽度为 7.3 m,吃水为 1.28 m,型深为 3.65 m,重心横向坐标值为1.2 m,排水量为 90 t。则快艇对试验船模的尺度比为9,试验船模的质量 m = 123 kg,重心坐标 xG= 0.2 m。为了计算方便,将快艇的艇体近似作为长方体来看待,利用相关公式估算出试验船模惯性矩 Ix= 0.71 m4,Iy= 17.3 m4,Iz= 0.18 m4。据经验公式, mx= 18.45 kg,my= 147.6 kg,mz= 147.6 kg,Jx= 0.35 Ix,Jy= 2 Iy,Jz= Iz。
接下来确定试验船模的最大运动参数,即列出六自由度平台的具体运动性能指标。由于国内外大型船舶水池所采用的运动装置大都为平面运动机构,考虑到采用这 2 种不同运动机构的试验装置所做的船模约束实验有很多是一样的,所以对六自由度平台运动性能指标的确定可以参考国内外平面运动机构。表 1 列出美国 DTMB 等 4 种平面运动机构的技术性能指标。
以表 1 为参考依据,同时考虑到试验装置应该同时满足教学和科研试验的要求,列出六自由度平台的具体运动性能指标。其中 6 个位移量除参考国内外平面运动机构外,还考虑到为满足教学与科研要求而将运动形式扩大到非线性运动,振荡圆频率取经验值,(角)速度和(角)加速度由位移量和振荡圆频率求得(位移 e = Acosht(角)速度 f = -Ahsinht(角)加速度 g = -Ah2cosht)。如表 2 所示(为了表示方便表格里的 e 和 f 值显示的是峰值变化)。
将所有已知参数的最大值代入到方程(7)到方程(12)中,得到计算结果 X = 10.1 N,Y = 198.6 N,Z= 149.8 N,K = 2.3 N·m,M = 12.8 N·m,N = 36.2 N·m。即可基本确定六分力天平的量程。

表 1 国内外平面运动机构技术性能指标Tab. 1 The technical performance of two-DOF platform at home and abroad
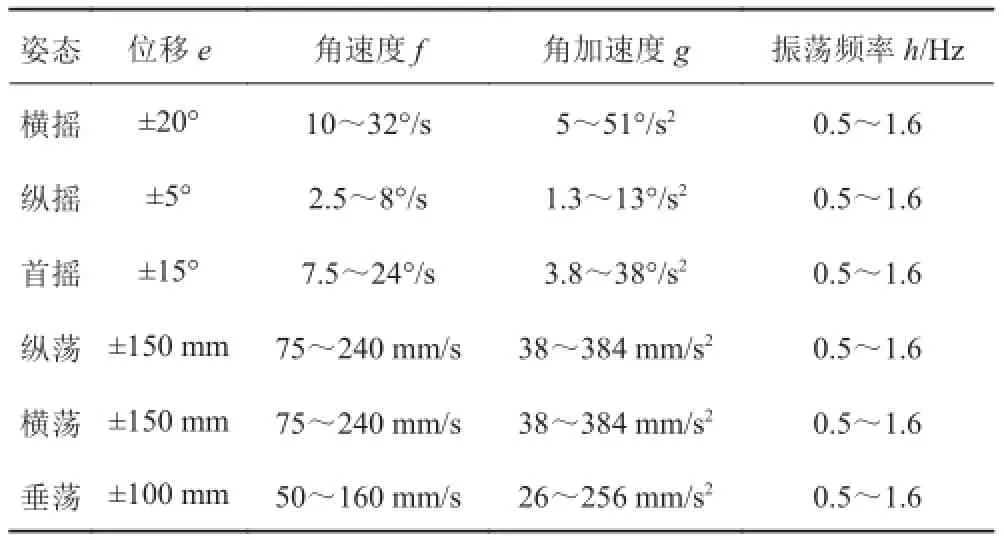
表 2 六自由度平台运动性能指标Tab. 2 The sports performance of six-DOF platform
3 测试装置的总体设计
华中科技大学船舶与海洋工程学院船模。船模试验水池长 175 m,宽 6 m,水深 4 m。以其为参考依据,设计出现有拖车平台的实际形状与尺寸,如图 2所示。由于 2 根横梁的形状较为细长,给尺寸的标注带来不便,所以画出横梁的局部视图,如图 3 所示。由于设计的拖车架是直接与 2 根横梁相连的,所以这对拖车架具体尺寸的确定具有重要意义。每根横梁的侧面都有 7 组定位孔,用于固定拖车架。
拖车平台本身比较狭长,且离水面的高度有限,即安装空间比较小。这就决定了六自由度平台应该从拖车架下面与拖车架连接,船模再与六自由度平台连接。而为了使拖车架和拖车架平台紧密连接,结合现有拖车平台的使用经验,应该让拖车架从平台上部扣住 2 根横梁。由此,新设计的拖车架要有 2 个接触面,同时与横梁的上面和下面固定。
从安装的可行性出发,将拖车架分为上下 2 个部分。上半部分的设计较为简单,参考现有拖车架的设计,上部分的形状应该为半工字型钢板。由于拖车架上半部分要与横梁一起承受来自拖车架下半部分与六自由度平台及试验船模的力和力矩,所以钢板应该具有一定的厚度和相当的长度,其接触面通过螺栓与横梁固定,两侧面通过螺钉固定,如图 4 所示。而拖车架的下半部分则要同时与横梁,拖车架上半部分和六自由度平台连接。
首先,为了让拖车架下半部分与横梁紧密连接,下半部分也应该包含一个半工字型钢板。为了方便与六自由度平台的连接,钢板也应该具有一定的厚度,而长度必须与上半部分一致。受到空间限制,拖车架上下 2 部分只能在 2 根横梁中间进行连接,为了保证连接精度与连接强度,宜采用面接触,同时为了限制拖车架的总重量,保证横梁的结构强度,可以将接触面分为 2 段。
而为了让接触面与拖车架下半部分通过螺栓连接成为一个整体,可以采用箱型结构,将其焊接在下半部分的半工字型钢板上。为更好地承受来自各个方向的力和力矩,箱型结构的横截面采用倒梯形;为了便于安装,箱型结构在横梁长度方向上要有大开口;为了保证箱型结构的稳定性,可以在其内部加装固定肋板。拖车架下半部分两侧面通过螺钉与横梁连接。
最后,受到空间限制,六自由度平台只能通过吊装从拖车架平台靠近水池的一侧与拖车架下半部分连接,为了便于安装,在下半部分的底部钢板上横向开出一个较深的倒梯形键槽,考虑到安装时的定位精度,键槽的长度小于钢板的宽度,同时通过螺栓固定,如图 5 所示。六自由度平台与试验船舶的装配方式则可以参照现有拖车架平台的连接方案,具体情况由船模的种类和大小决定,两者之间的连接部分用于安装六分力天平和相关传感器。整个测试装置的二维示意图如图 6 所示,三维示意图如图 7 所示。
整个测试装置中拖车架上半部分和 2 根横梁是主要受力部分,为了计算方便,认为两部分在长度方向上的受力是均匀的。均布载荷包括拖车架自身重量和附加载荷,钢材的密度为 7.85 g/cm3,附加载荷定为 500 kg。容易算出拖车架上半部分的均布载荷为 6.08 kN·m,下半部分的均布载荷为 3.04 kN·m。用 Ansys 软件对拖车架上半部分和横梁进行建模分析。图 8 和图 9 分别为拖车架上半部分和横梁的受力云图。
从图中可以看出拖车架上半部分与横梁所受最大应力分别为 2.07 MPa 和 74.8 MPa,分别小于 195 MPa和 290 MPa 的屈服极限。通过 Ansys 软件分析,可以得出结论:设计的测试装置在结构强度方面是满足要求的。由此制造出六自由度船模水动力性能测试装置的实物。图 10 为整个测试装置的实物图。
4 结 语
本文对一种新型船模水动力性能测试装置进行了系统研究,构建了测试装置的基本框架,对其中的 3个重要组成部分,即六自由度平台,六分力天平与拖车架进行了一定深度设计、分析与探讨。这种新型船模水动力性能测试装置将有效地提高船舶水动力导数的测量范围,对船舶水动力导数相关领域的科学研究将起到积极的推动作用。
[ 1 ]STEWART D. A platform with six degrees of freedom[J]. Proceedings of the Institution of Mechanical Engineers, 1965, 180(1): 371-386.
[ 2 ]洪鸣, 刘相波, 于魁龙. 六自由度运动平台控制系统[J]. 兵工学报(坦克装甲车与发动机分册), 1996(1): 13-18. HONG Ming, LIU Xiang-bo, YU Kui-long. The control system of six -DOF motion platform[J]. Industry and Technology (Tanks, Armored Vehicles with Engine Volumes), 1996(1): 13-18.
[ 3 ]苏玉鑫, 段宝岩. 六自由度 Stewart 平台运动精度分析[J]. 西安电子科技大学学报(自然科学版), 2000, 27(4): 401-403, 413. SU Yu-xin, DUAN Bao-yan. The kinematics accuracy analysis of six-DOF Stewart[J]. Journal of Xidian University, 2000, 27(4): 401-403, 413.
[ 4 ]王勇亮, 齐丽君, 梁建民. 位移传感器在六自由度运动平台中的应用[J]. 传感器技术, 2003, 22(4): 49-50. WANG Yong-liang, QI Li-jun, LIANG Jian-min. Application of displacement sensor in 6 DOF motion platform[J]. Journal of Transducer Technology, 2003, 22(4): 49-50.
[ 5 ]何景峰, 韩俊伟. 六自由度运动平台冲击响应分析[J]. 哈尔滨工业大学学报, 2005, 37(10): 1391-1393. HE Jing-feng, HAN Jun-wei. Shock response analysis of 6-DOF parallel motion platform[J]. Journal of Harbin Institute of Technology, 2005, 37(10): 1391-1393.
[ 6 ]荣辉, 范培卿, 丁洪生. 六自由度并联平台的灵敏度分析与参数优化[J]. 机械设计与研究, 2007, 23(1): 34-36. RONG Hui, FAN Pei-qing, DING Hong-sheng. Sensitivity analysis and parameters optimization for six degree-of-freedom parallel platform[J]. Machine design and research, 2007, 23(1): 34-36.
[ 7 ]杨达毅, 陈丽敏. 基于 SolidWorks 的六自由度液压平台运动仿真[J]. 机床与液压, 2008, 36(9): 127-129, 150. YANG Da-yi, CHEN Li-min. Motion simulation of 6-DOF hydraulic servo platform based on SolidWorks[J]. Machine Tool & Hydraulics, 2008, 36(9): 127-129, 150.
[ 8 ]杨鹏. 船舶六自由度运动模拟台及其控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2008. YANG Peng. Research of ship six degrees of freedom motion simulation platform and its control method[D]. Harbin: Harbin Engineering University, 2008.
[ 9 ]高飞. 一种六分力传感器的数值计算与分析[D]. 武汉: 武汉理工大学, 2006. GAO Fei. The numerical calculation and analysis on six-force sensors[D]. Wuhan: Wuhan University of Technology, 2006.
[10]张秀凤, 尹勇, 金一丞. 规则波中船舶运动六自由度数学模型[J]. 交通运输工程学报, 2007, 7(3): 40-43. ZHANG Xiu-feng, YIN Yong, JIN Yi-cheng. Ship motion mathematical model with six degrees of freedom in regular wave[J]. Journal of Traffic and Transportation Engineering, 2007, 7(3): 40-43.
A new hydrodynamic testing device of model ship
YANG Hang1, TU Hai-wen1, XIE Wen-xiong1, SUN Jiang-long1,2,3
(1. School of Naval Architecture and Ocean Engineering (HUST), Wuhan 430074, China; 2. Hubei Key Laboratory of Naval Architecture and Ocean Engineering Hydrodynamics (HUST), Wuhan 430074, China; 3. Collaboration Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai 200240, China)
Nowadays, all hydrodynamic testing devices of model ship are planar motion mechanism, thus limiting the measuring range of ship hydrodynamics, while a new hydrodynamic testing device of model ship, the six-DOF hydrodynamic testing device can expand it. It is introduced in three ways: the works of six-DOF platform, the method for determining the range of six-component balance, the total design. Firstly, the works of six degrees of freedom platform is introduced in detail,. that the correspondence between the movement of the six sports bars on the platform and the six freedom movement of a ship. Then establishing preliminary equations to calculate the forces and moments of the six freedom movement, and determining the range of six-component balance in the experiment device on the basis of specific technical performance of the planar motion mechanism at home and abroad. Finally, the overall structure of the experiment device is determined and the shape and size of the existing ship pool trailer platform are designed. On this basis, the specific structure and size of the trailer frame, the three-dimensional schematic diagram, two-dimensional installation diagram and size diagram can be determined, considering forces of the trailer platform and installation of the trailer platform and six degrees of freedom platform, and do structural strength analysis.
six DOF;testing device;six-component balance
U661.1
A
1672 - 7619(2017)02 - 0031 - 06
10.3404/j.issn.1672 - 7619.2017.002.006
2016 - 02 - 29;
2016 - 04 - 20
国家自然科学基金资助项目(51474109)
阳航(1994 - ),男,硕士研究生,研究方向为船舶水动力性能。

