数值模拟技术在定日镜风载荷计算中的应用

程　松

上海电气集团股份有限公司 中央研究院　上海　200070

数值模拟技术在定日镜风载荷计算中的应用

程松

上海电气集团股份有限公司 中央研究院上海200070

利用Fluent流体动力学仿真软件对风场中的定日镜模型进行数值模拟计算，得到反射镜面上的平均风压因数及风压分布，并与风洞试验结果进行对比和分析。通过对比分析确认，数值模拟得到的定日镜风压因数与风洞试验结果一致，表明数值模拟技术可以用于定日镜风载荷计算。

数值模拟；定日镜；风载荷；计算；应用

1　研究背景

在太阳能热利用的各种方式中，塔式太阳能热发电技术代表了规模化利用太阳能的发展趋势，是太阳能热发电技术的制高点。在塔式太阳能热发电系统中，定日镜场实现太阳辐射能的聚集，是整个系统的主要组成部分。在西班牙、美国等发达国家，塔式太阳能热发电技术已经应用于多个商业化运营项目。目前，大规模推广塔式太阳能热发电技术的主要障碍之一是较高的建设成本。火力发电站的建设成本一般小于1万元/kW，而塔式太阳能热发电站的建设成本超过2万元/kW[1]。在塔式太阳能热发电站中，定日镜场由几千至几万台定日镜单元组成。在已建成的塔式太阳能热发电站中，定日镜场投资占总投资的50%以上[2]，是电站建设投资的主体部分。可见，对定日镜的单体成本控制有助于降低塔式太阳能热发电系统的投资成本，提高大规模利用塔式太阳能热发电技术的可行性。

降低机械装置的成本是定日镜整机成本控制最直接和最有效的方式。对定日镜进行成本控制时，必须合理确定定日镜的机械载荷参数，为定日镜的结构优化提供合理约束。由于定日镜通常工作于野外环境中，整体呈T形结构，并采用平板结构反射太阳入射光，因此风载荷是定日镜的主要设计载荷。在建筑结构设计中，结构的风载荷体形因数通常通过风洞试验方法确定。虽然风洞试验方式具有较高的可信度，但这种方法成本高昂，而且试验周期长。随着计算机技术和信息技术的快速发展，通过数值计算方法确定建筑结构的风载荷体形因数具有了可能性。

为了确定定日镜镜面的风压分布和平均风压因数，笔者应用Fluent数值模拟软件进行定日镜某一姿态时的风载荷计算，并将计算结果与风洞试验结果进行比较，确认数值模拟方法能适用于定日镜的风载荷计算。

2　计算域确定及网格划分

笔者的研究对象为定日镜，结构呈T形，上部设置平面反射玻璃。反射面呈矩形，用以将太阳辐射能反射到镜场的指定位置。定日镜外形结构如图1所示，宽为1.4m，高为0.8m，离地0.2m，反射玻璃厚度为4mm。

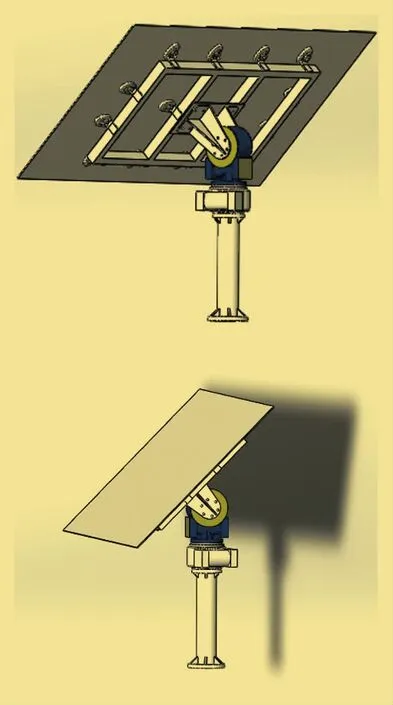
图1　定日镜外形结构

在流体动力学计算中，计算域一般是立方体，并需要有足够的空间尺寸，以确保足够的精度。为了保证流体计算域中空间结构堵塞度小于5%，笔者将计算域确定为入口方向深度5.7m，出口方向深度17.1m，两侧壁方向宽度5.7m，底部与顶部之间距离4m，流体计算域如图2所示。

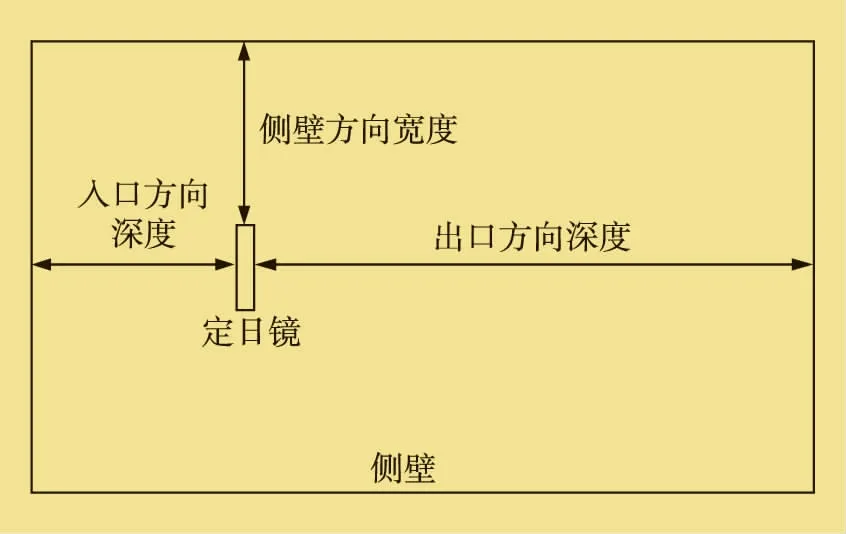
图2　流体计算域示意图

在正常工况下，定日镜反射面竖直放置，支撑结构将承受最大的风载荷。定日镜竖直放置姿态如图3所示[3]。

图3　定日镜竖直放置姿态

流体计算域网格的划分存在一个矛盾： 从提高计算精度的目标出发，需要将计算域进行密集划分；而从提高计算速度的目标出发，需要将计算域进行较稀疏的划分[4]。在确保一定计算精度的前提下，加快计算速度，采用混合网格划分方式，在靠近定日镜结构的区域使用加密网格，而在其它外部区域则采用较为稀疏的网格，两个区域之间逐步过渡，以保证定日镜区域可得到较为精确的计算解。笔者应用Gambit软件进行网格划分，采用网格间隔计数功能[5]，设置网格密度从定日镜位置的密集状向四周的稀疏状逐渐过渡。计算域网格划分如图4、图5所示，网格数为163612。

图4　计算域整体网格划分

图5　计算域去除大气后网格划分

3　湍流模型控制与边界条件设定

大气环境下的近地风在风洞试验中被认为是一种不可压缩的湍流流动，通常可采用分离式求解器进行计算。

由于定日镜反射面区域的近地风含有大量湍流，因此笔者使用标准k-ε湍流模型进行湍流计算。这一模型是从试验中总结出的一个半经验公式，是目前使用最广泛的湍流模型，在湍流动能k方程的基础上，再引入湍动耗散率ε。这一模型假设流动为完全湍流，分子黏性不考虑，计算量小，收敛速度快，特别适合于绕流、边界层流动或有部分回流的问题。

近地风与地面之间会产生摩擦力，由于这个摩擦力的存在，靠近地面处的风速将受到削弱，且摩擦力的影响随高度的增加而逐步减弱。当超过某一特定高度时，地面摩擦力的作用对风速的影响极小，可以忽略不计。这个高度称为大气边界层厚度，一般为300～500m。根据我国国家标准[6]，大气边界层以内各高度的风速采用指数型梯度风速，其表达式为：

v(z)/vb=(z/b)α

(1)

式中：z为高度，m；v(z)为高度z处的风速，m/s；b为标准高度，按照我国国家标准，b=10m；vb为标准高度b处的风速，m/s；α为地面粗糙度指数，根据我国国家标准，乡村等B类地貌下α=0.15。

定日镜计算域的出口条件采用完全发展的流出边界条件。计算域的顶部和侧壁采用对称边界条件，等价于黏性流动中的自由滑移壁面。定日镜反射玻璃表面和地面的边界条件均采用无滑移壁面条件。

关于定日镜计算域的入口条件，根据式(1)，在Fluent中采用自定义函数对入口风速边界条件进行自定义，在标准高度10m处的基本风速为 8m/s。

4　结果分析

定日镜面平均风压因数指定日镜表面任意一点的风压与参考点处平均风压的比值，表征风载荷对定日镜表面任意一点作用力的相对大小。根据流体动力学实践经验，相似体形的结构具有基本一致的平均风压因数分布趋势。参考点可以取某一高度处的平均风速，实际笔者取定日镜的中心点高度0.6m。平均风压因数Cp的定义式[7]为：

Cp=2p/(ρV2)

(2)

式中：ρ为标准大气密度,kg/m3,ρ=1.225kg/m3；V为参考点高度的风速，m/s，根据式(1)，V=5.246m/s；p为定日镜反射表面任意一点的风压值，Pa。

经过Fluent软件1000次数值迭代计算后，定日镜迎风面和背风面的平均风压因数分布如图6所示。

图6　定日镜平均风压因数分布图

目前有关结构表面风压的研究多集中于高层、大跨度、低矮房屋等结构，对于定日镜这种体形结构的风洞试验数据较少，可检索到的部分公开试验数据有我国湖南大学和美国Sandia实验室进行的风洞试验。湖南大学风洞试验中，定日镜模型呈矩形，高为1.2m，宽为0.9m，与笔者的定日镜样机几何尺寸相近。根据流体动力学的相似理论，两者定日镜的表面有基本相似的风压因数分布趋势。在湖南大学定日镜模型风洞试验中[8]，定日镜的仰角和风向角都为0°，即反射面呈竖直姿态，这时定日镜模型的平均风压因数分布如图7所示。

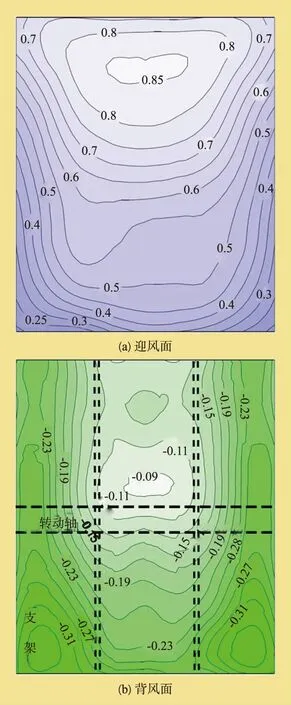
图7　湖南大学风洞试验定日镜平均风压因数分布图

以下对图6与图7进行对比分析。

(1) 两者的迎风面和背风面平均风压因数分布趋势一致。

(2) 定日镜的迎风面平均风压因数呈现正压分布现象，背风面呈现负压分布现象。

(3) 定日镜的迎风面平均风压因数在同一高度位置呈现中间大，且中间向两边递减的现象。迎风面的最大风压位置不是定日镜的中心点，而是位于定日镜中心的上部。迎风面的最小风压位置位于定日镜的四个边角及下边沿。

(4) 背风面绝对值最小的负压区域位于定日镜中心的上部和镜面边缘，而在背风面两侧附近形成了绝对值较大的负压分布带。

(5) 定日镜背风面的平均风压因数分布相比迎风面更复杂，这是由于气流在定日镜的反射面边沿发生分离，在定日镜背面区域形成气流旋涡，造成定日镜背风面风压分布复杂。

参考点的平均风压ω0根据伯努力公式[9]进行计算：

ω0=ρV2/2

(3)

定日镜整体风载荷风洞试验与计算结果见表1。笔者在Fluent数值模拟计算时，定日镜的整体风载荷主要表现为风的阻力，为29.1N。定日镜整体风载荷因数C为：

根据Sandia实验室公布的定日镜风载荷报告[10]，仰角和风向角都为0°时，定日镜模型整体风载荷因数约为2.0，而湖南大学风洞试验的结果约为1.4[11]。定日镜仰角和风向角都为0°时，结构承受最大风载荷，这是结构设计要考虑的主要工况。

当定日镜的反射面呈竖直姿态时，定日镜的风载荷主要为风的阻力，笔者通过数值模拟计算方法，得到的定日镜风载荷因数与湖南大学风洞试验结果基本相同。此外，由于笔者仿真计算的定日镜反射面采用理想化的平板形状，没有考虑镜面支撑、转动轴及支撑臂构件对风力的遮挡和干扰作用，导致试验结果偏大，这与Sandia实验室风洞试验结果原理相似。综上所述，数值模拟计算的结果符合风洞试验情况，是可信的，可以应用于风载荷主要工况的结构设计和计算中。

表1　定日镜整体风载荷

5　结论

采用计算机数值模拟方法可以得到定日镜的表面风压分布和整体风载荷等数据，与风洞试验得到的结果进行比较，两者基本吻合，表明通过数值模拟方法能够为定日镜的风载荷结构设计提供合理的参考数据。此外，数值模拟方法还可以得到定日镜周围的风压流场分布，为定日镜的表面风压分布现象提供合理解释。

[1] 王轶辰.太阳能光热发电之路如何走？——我国光热发电产业调查[N].经济日报，2016-11-14(12).

[2] 徐能，田军，李心，等.塔式太阳能热发电站单塔最优装机容量分析[J].太阳能，2015(12)： 50-55.

[3] 北京兆迪科技有限公司.SolidWorks快速入门教程(2013中文版)[M].北京： 机械工业出版社，2013.

[4] 王福军.计算流体动力学分析——CFD软件原理与应用[M].北京： 清华大学出版社，2004.

[5] 韩占忠，王敬，兰小平.FLUENT——流体工程仿真计算实例与应用[M].2版.北京： 北京理工大学出版社，2004.

[6] 建筑结构荷载规范： GB 50009—2012[S].

[7] 张相庭.结构风压和风振计算[M].上海： 同济大学出版社，1985.

[8] 王莺歌.塔式太阳能定日镜结构风荷载特性及风致响应研究[D].长沙： 湖南大学，2010.

[9] 黄本才.结构抗风分析原理及应用[M].上海： 同济大学出版社，2001.

[10] PETERKA J A, DERICKSON R G. Wind Load Design Methods for Ground-based Heliostats and Parabolic Dish Collectors[R].1992.

[11] 宫博.定日镜和幕墙结构的抗风性能研究[D].长沙： 湖南大学，2010.

(编辑： 平平)

The numerical simulation of the heliostat model in the wind field was carried out by Fluent hydrodynamic simulation software. The average wind pressure factor and wind pressure distribution on the reflector surface were obtained and compared with the wind tunnel test results for analyses. By comparative analysis it is confirmed that the wind pressure factor obtained by numerical simulation is consistent with the wind tunnel test results and it shows that the numerical simulation can be used to calculate the wind load of the heliostats.

NumericalSimulation；Heliostat；WindLoad；Calculation；Application

TM714

B

1674-540X(2017)04-045-05

2017年7月

程松(1976—)，男，硕士，高级工程师，主要从事塔式太阳能热发电控制研究工作，E-mail： chengsong@shanghai-electric.com