双馈风力发电系统矢量控制研究
许湖江
上海交通大学 电子信息与电气工程学院 上海 200240
双馈风力发电系统矢量控制研究
许湖江
上海交通大学 电子信息与电气工程学院上海200240
基于定速与变速风电系统的运行特性,得出了变速风力发电系统的优点。在变速风力发电系统工作原理的基础上,提出了动态模型方程,并论述了双馈风力发电系统的矢量控制理论。对 1.5MW 双馈风力发电系统进行了计算机仿真与实际运行试验,验证了所论述理论的正确性。
风力发电;矢量控制;仿真;试验
1 研究背景
为应对日益凸显的环境危机及能源危机[1],作为可再生能源中最成熟的技术,风力发电得到了全球各国的高度重视。风力发电系统的目的是最大限度获取风能,提高风力发电机组的输出功率。2000年前,风力发电机组单机输出功率还只是千瓦级别,最大额定功率只有200kW,但是到了2000年之后,市场上主流的风力发电机组输出功率达到了兆瓦级别。预计在不久的将来,风力发电机的额定功率将进一步增大,特别是在海上风电的应用中。2016年,两大风电巨头维斯塔斯与西门子在欧洲安装了各自研发的 8MW 样机,使国际海上风电正式进入了8MW时代。目前市场上主流的风力发电机参数见表1,这些风力发电机均为变桨距及变速控制。

表1 主流风力发电机参数
早期安装的小容量风力发电系统,选用简单的鼠笼式异步感应发电机,将风能转化为电能直接连接至三相电网,其风轮转子通过固定传动比率的齿轮箱直接连接到发电机主轴上。也有一些感应发电机使用极点可调的绕组配置来实现风力发电机在不同同步转速下的运行。上述类型的风力发电机必须在恒定速度下运转,不能变速运行,这种恒速风力发电系统的结构及性能非常依赖于机械结构的设计及电力电子电路的特性。由于风能特有的不确定性,每当一阵风吹到风力发电机组上时,可以看到系统的输出功率会有一个非常快速且强烈的变化。负载的变化不仅需要一个稳定的电网系统来维持,而且需要非常稳固的机组机械结构来吸收变化过程中产生的高机械应力,尤其是对于额定功率比较高的机组,使用恒速风电系统会导致成本昂贵。因此,目前市场上的主流设计为变速风力发电系统。
2 变速风力发电系统
目前市场上主流的大容量风力发电机组大都采用变速运行的技术方案[2],与恒速风力发电机组相比,变速风力发电机组具有以下主要优点。
(1) 具有显著的成本效益,可对桨距角进行控制[3]。发电机的控制速度可以允许桨距角控制时间变得更长,从而降低变桨距控制的复杂性,以及峰值功率要求。当在低风速情况下时,桨距角通常是固定的;而当处于超过额定功率对应的风速时,执行桨距角控制,最终限制机组最大功率的输出。
(2) 降低机组运行时的机械应力,吸收偶然性阵风,能量可以被储存在风力发电机的机械惯性中,从而减小机械转矩的振荡。
(3) 提高电能质量,减小输出功率的瞬间变化。
(4) 提高系统的工作效率,使风力发电机组始终在最大功率点附近运转[4-5]。
(5) 降低风力发电机运行的噪声。
3 双馈风力发电系统
变速恒频双馈风力发电系统是目前风电行业应用最广泛、技术最成熟的风电技术之一。图1为典型的变速恒频双馈风力发电系统,系统中包括了双馈发电机、功率变换器等部件。双馈发电机的定子端直接与电网相连接,转子端则通过一组交-直-交背靠背脉宽调制变流器与电网相连,变流器为转子绕组提供励磁电流。根据双馈发电机定转子的电磁关系可知,变流器只需要提供转差功率,即最大30%额定功率便可实现双馈风力发电系统的变速恒频运行与最大功率追踪[6],大大降低了变流器的容量,节约了成本。此外,通过改变励磁电流的相位与幅值,可以实现发电机输出有功功率与无功功率的解耦控制,提高风电场功率调度的灵活性。
3.1 数学模型
为了研究双馈风力发电系统的动态性能,以及有功无功功率的解耦控制[7],需要讨论双馈风力发电系统的动态数学模型。由于双馈风力发电机与普通绕线式异步发电机在电机结构方面类似,因此可以参考普通异步发电机的理论进行分析与研究。设双馈风力发电机定子端正方向采用发电机惯性,转子端正方向采用电动机惯性,基于磁势与电势平衡理论,可以得到双馈风力发电机的等效电路,如图2所示,其数学基本方程式为:
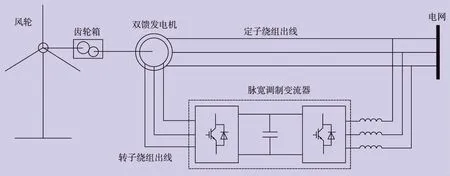
图1 典型变速恒频双馈风力发电系统

图2 双馈风力发电机等效电路
(1)
式中:U1为定子侧电源电压;U2为转子侧馈电电压;E1为定子侧感应电动势;S为发电机转差率;E2为转子侧感应电动势;Em为互感感应电动势;i1为定子电流;i2为转子电流;im为互感电流;r1与X1分别为定子绕组电阻与漏抗;r2与X2分别为转子绕组电阻与漏抗;rm与Xm分别为励磁互感回路电阻与漏抗。
当机组的额定电压、额定功率及功率因数一定时,双馈风力发电机实际上只有S、U2,以及U2与U1相位差角度之间的关系,即可通过调节双馈发电机组幅值、频率及相位来控制输出。
由双馈风力发电系统在三相静止坐标系下的物理模型,可以得到机组在三相静止坐标系下的数学模型。在该数学模型中,双馈风力发电机定子与转子的互感应与转子位置角有关,发电机数学模型为时变非线性、高阶微分方程,磁链则具有强耦合关系,电感的矩阵较复杂,很难得到它的解析解,想要对双馈风力发电系统进行控制就更加困难了。因此基于以上考虑,对双馈风力发电系统数学模型进行简化,并进行解耦磁链。
将三相静止坐标系变换到d-q两相同步参考坐标系,这一等效变换是在磁势一致的前提下进行的。在完全对称的三相静止绕组中,三相交流电流过后可叠加为一个旋转磁势F,该磁势按照正弦分布的形式在空间中以同步转速ω1,即电流角频率进行旋转,不同相的绕组可认为在相应的坐标系上所产生的磁势F是相同的。通过以上方法,双馈风力发电系统的数学模型可以得到较大简化。
一般情况下,将三相静止绕组等效为两个相同匝数并且互相垂直的旋转绕组d1、q1,当d、q两轴的电流id1与iq1流过这两个绕组时,合成的磁势相对于d1、q1绕组是静止的,所以合成磁势等效为一个空间的磁势。通过控制d1、q1绕组中流过的电流大小来控制旋转磁场的转速和大小,从而保持与坐标系下的旋转磁势F相一致,这样就达到了使用旋转d1、q1绕组来取代三相静止绕组的目的。图3为旋转d-q坐标系下的双馈风力发电机绕组等效物理模型,其中uq1s、uq1r、ud1s、ud1r对应代表双馈风力发电机定转子绕组在d、q轴上的电压。
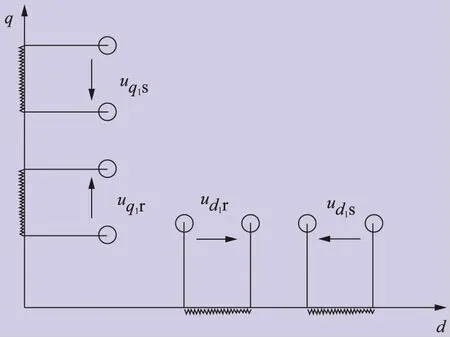
图3 旋转d-q坐标系下双馈风力发电机绕组等效物理模型
依据坐标变换,在保证磁势不变的情况下,三相静止坐标系变换到d-q坐标系的数学矩阵ks(θ)为:
(2)
式(2)中θ为静止坐标系A轴与d-q坐标系d轴的夹角,并随时间的改变而改变。
d-q坐标系的旋转角速度ω=dθ/dt,同时ω=ω1。
经过坐标变换,由式(1)、式(2)转换可得d-q坐标系下的电流方程为:
(3)
式中:iq1s为q轴定子绕组电流;Xls为定子电抗;Xlr为转子电抗;Ψq1s为q轴定子磁通;Ψmq1为q轴互感磁通;id1s为d轴定子绕组电流;Ψd1s为d轴定子磁通;iq1r为q轴转子绕组电流;Ψq1r为q轴转子磁通;id1r为d轴转子绕组电流;Ψd1r为d轴转子磁通。
互感磁通的方程为:
(4)
式中:Ψmd1为d轴互感磁通;Xm1为互感励磁电抗。
磁通方程为:
(5)
式中:ωb为电磁场旋转角速度;ωr为转子旋转角速度;Xaq1和Xad1分别为q、d轴电枢反应电抗参数。
(6)
电磁转矩Te方程及转子旋转角速度方程分别为:
(7)
(8)
式中:TL为作用于轴上的机械转矩;J为电机转动惯量;P为发电机极对数。
3.2 矢量控制
双馈风力发电系统是一个多变量、强耦合、复杂多变的非线性系统,需要对双馈风力发电机组的数学模型进行解耦控制,而矢量控制则是实现解耦的关键技术。双馈风力发电机定转子的电流分量为工作频率量和转差频率量,它是一个高阶非线性强耦合多变量系统,如果简单地对交流电进行闭环控制而不进行解耦,得到的效果并不理想。矢量控制可在坐标变换理论的基础上,使双馈风力发电机内部各变量之间的耦合关系得到简化,从而可使双馈风力发电机的控制得到简化。
双馈风力发电系统应用矢量控制策略,解耦电磁转矩和转子励磁控制,使q轴的定子磁通量得到消除,由此,电磁转矩方程式可以写为:
Te=-3PXm1imsiq1r/2
(9)
式中:ims为定子侧互感励磁电流。
由式(9)可以得出,Te能通过控制q轴转子绕组电流iq1r来直接控制双馈风力发电机的转子转速,因此,对于一个给定的输入机械转矩TL,双馈风力发电机的输出功率就能被控制。无功功率的控制也可以由q轴转子绕组电流iq1r来实现控制。
为确保系统的稳定运行,并能独立控制双馈风力发电机组的有功与无功功率输出,设计了双馈风力发电系统矢量控制器,如图4所示。
图4中IRdq和VRdq分别为两相d-q坐标系下的转子电流与电压,IS dq为两相d-q坐标系下的定子电流,VR和IR分别为双馈风力发电机侧变流器转子电压与电流,VS和IS分别为电网侧变流器定子电压与电流,VDC为变流器直流母线电压,PG和QG分别为双馈风力发电机的有功和无功功率,PGset和QGset分别为双馈风力发电机的有功和无功功率参考值,ΦVS和ΦVR分别为双馈风力发电机定子和转子电压矢量角,IGC为电网侧变流器控制电流,IN为双馈风力发电机额定电流。
根据图4测量得到的转子电流信号可用于转子电流的调节,以减小参数失谐,以及变流器增益误差的影响。
4 仿真结果
为了评估双馈风力发电系统矢量控制[8-9]的效果,基于MATLAB软件Simulink仿真模块,对双馈风力发电系统进行了仿真模拟分析[10]。图5为双馈风力发电系统在不同转速比下的瞬时有功功率随时间变化响应曲线。由图5(a)可知,当解耦控制未被激活,即使用基于滑移控制的基本稳态电压模型来控制机组系统时,由于d、q两轴变量之间的耦合,系统性能取决于响应速度。由图5(b)可知,根据双馈风力发电系统的动力学模型进行解耦控制时,系统响应的速度较快且平稳。
5 试验结果
在国产典型1.5MW双馈风力发电机组上进行试验,系统的额定功率为1.5MW,双馈风力发电机额定转速为1800r/min,试验结果如图6~图10所示。
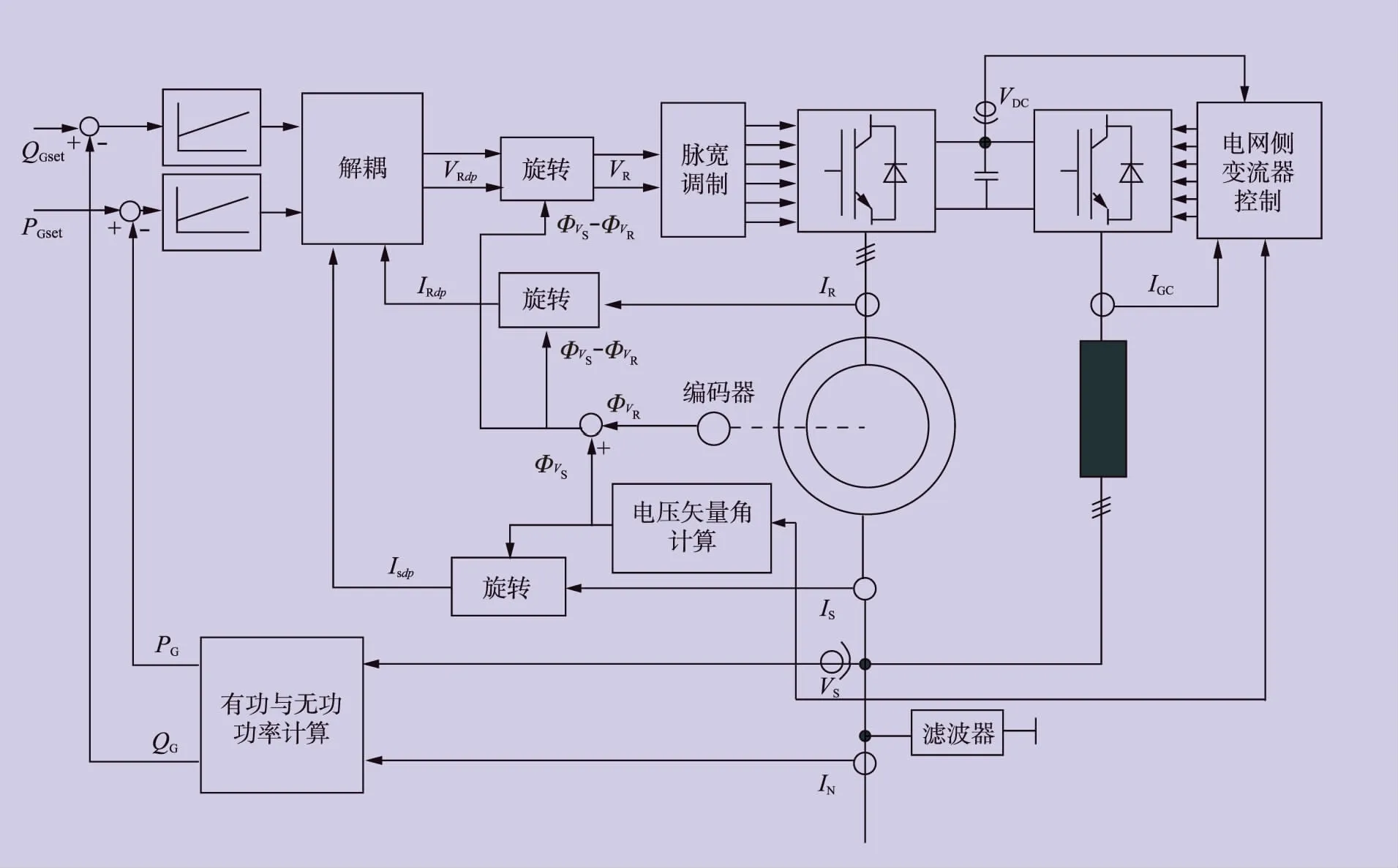
图4 双馈风力发电系统矢量控制器

图5 双馈风力发电系统在不同转速比下的瞬时有功功率随时间变化响应曲线

图6 运行试验风速波形

图7 运行试验转子转速波形
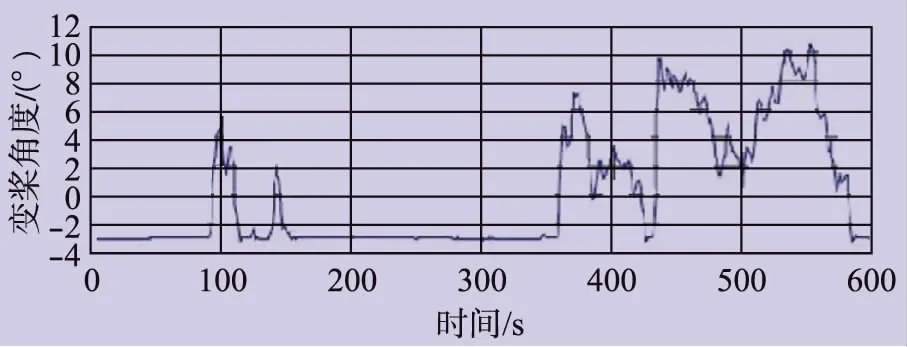
图8 运行试验变桨角度波形
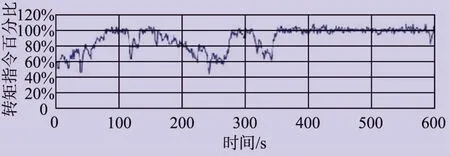
图9 运行试验转矩指令百分比波形

图10 运行试验输出功率波形
机组主要使用变桨控制来控制风力发电机的转速。当时间为350s时,由于机组未达到最大输出功率,此时变桨控制不是很有效,因此,系统跟踪最大功率曲线来达到最大功率输出。当时间长于350s时,可看到风速达到15m/s,机组系统将转矩指令百分比限制在100%,且系统传输到电网的实际输出功率完美匹配了设定的控制指令。在恒定最大功率模式下,变桨系统将风轮叶片速度控制在一定范围内,在短时间内风速达到18m/s,但变桨控制系统并没有跟踪阵风。在此瞬态过程中,输出功率几乎保持恒定,保证了电能质量,维护了电网的稳定。
6 结论
对于大容量并网型风力发电系统,使用变速调节风力发电机组是最理想、最具经济效益的技术方案。
笔者推导了双馈风力发电系统数学模型,设计了矢量控制器,并以此来解耦及对无功功率进行控制,仿真结果及1.5MW双馈风力发电机组实际运行试验数据验证了理论的正确性。
[1] 罗承先.世界风力发电现状与前景预测[J].中外能源,2012,17(3): 24-31.
[2] 谭超.变速恒频双馈风力发电系统控制技术研究[D].长沙: 湖南大学,2013.
[3] 缪新磊,秦栋平.运动控制在变桨控制系统中的应用[J].上海电气技术,2016,9(2): 49-51,63.
[4] 刘其辉,贺益康,赵仁德.变速恒频风力发电系统最大风能追踪控制[J].电力系统自动化,2003,27(20): 62- 67.
[5] 贺益康,胡家兵.双馈异步风力发电机并网运行中的几个热点问题[J].中国电机工程学报,2012,32(27): 1- 15.
[6] 辜承林,韦忠朝,黄声华,等.对转子交流励磁电流实行矢量控制的变速恒频发电机——(第一部分: 控制模型与数值仿真)[J].中国电机工程学报,1996,16(2): 119-124.
[7] 刘新宇.大型双馈风力发电机组并网转子励磁控制技术研究[D].郑州: 郑州大学,2013.
[8] 孙佳林,奚玲玲.兆瓦级风力发电机运行流程与安全策略的研究与实践[J].上海电气技术,2009,2(4): 33- 36.
[9] TANG Y, XU L. A Flexible Active and Reactive Power Control Strategy for a Variable Speed Constant Frequency Generating System[J]. IEEE Transactions on Power Electronics,1995,10(4): 472-478.
[10] 訾鹏,周孝信,田芳,等.双馈式风力发电机的机电暂态建模[J].中国电机工程学报,2015,35(5): 1106- 1114.
(编辑: 平平)
Based on the operating characteristics of fixed speed wind power system and variable speed wind power system, the advantages of variable speed wind power generation system were obtained. Based on the working principle of variable speed wind power generation system, the dynamic model equation was put forward, and the vector control theory of DF wind power generation system was discussed. The computer simulation and practice service test of 1.5 MW DF wind power generation system were carried out to verify the validity of the theory.
WindPowerGeneration;VectorControl;Simulation;Test
TM315
A
1674-540X(2017)04-021-06
2017年5月
许湖江(1986—),男,本科,工程师,主要研究方向为风力发电系统控制与技术,E-mail: xuhj198603@163.com

