型煤峰后渗透特性试验研究*

马建宏，候　超，信长喻，李建明

(1. 河南理工大学，河南 焦作 454000；2. 煤炭安全生产河南省协同创新中心，河南 焦作 454000； 3. 郑州煤炭工业(集团)有限公司，河南 郑州 450000)

0　引　言

瓦斯事故一直是我国煤矿五大灾害之首，中国也已经成为世界上瓦斯灾害最为严重的国家，矿井瓦斯真正受到人们的普遍关注是在20世纪，且多半是由于瓦斯所造成的灾害事故[1]，，面对这种严峻的局面，国内外学者开展了大量关于煤体渗透特性的研究。1984年，S.HarPaalni[2]与J.Gawuga[3]以煤层赋存的地质条件为前提，探讨了含瓦斯煤样在受载状况下的渗透特性。V.Khodot[4]学者以煤层赋存的地物场环境和地质条件为前提，探讨了含瓦斯煤样的力学状况，系统的分析了瓦斯渗流和煤岩体之间的固气力学特征。1997年，Enever[5]通过研究含瓦斯煤层的渗透性与有效应力之间的互相影响，总结出了煤层中应力的增量和渗透能力变化表示出指数特征。其后，周世宁和林柏泉[6]进行了模拟实验，探讨了原岩应力环境对瓦斯的渗透性能作用。仵彦卿[7]通过岩体渗流与应力关系测试，总结出岩体渗透系数与有效应力存在幂指数关系。李树刚[8]初次提出了煤样渗透系数—体积应变方程，该方程基于采场卸压瓦斯的运移规律明显受矿山压力影响的原理[9]。梁冰、刘建军[10]对差别温度下煤岩应力和瓦斯压力的分布规律进行了数值模拟创立了考虑温度场、应力场和渗流场的固气耦合数学模型。赵延林、曹平[11]等，以岩体结构力学和细观损伤力学为依据，建立了合适的裂隙岩体渗流-损伤-断裂耦合数学模型。唐春安[12]研究团队在分析岩石破裂过程中渗透率演化时，基于统计损伤力学建立了裂隙损伤同渗透率演化的耦合模型。刘先珊等[13]以现有裂隙变形曲线的研究成果为依据，创立了渗透系数与卸荷应力、应变间的本构关系。许江[14]等运用三轴渗透装置开展了不同环境温度和不同有效应力条件下长期荷载作用前后含瓦斯煤的渗透率演化试验研究，并在此基础上分析了长期荷载作用前后煤样渗透率对有效应力以及环境温度的敏感性。 袁欣鹏[15]等为研究井下卸压抽采时瓦斯流动规律，建立煤层渗透率演化模型，从应力条件和孔隙压力2个方面，结合煤样渗透率试验，对该模型进行有效性验证。

随着科学技术的发展，瓦斯抽采技术在各个矿区应用，我国在煤体渗透特性演化规律研究方面已取得了一些成果，在一定程度上较好的指导了煤矿开采过程中的瓦斯抽采及增透技术。目前存在的问题主要是针对型煤峰值强度后的渗透率演化特征研究较少。所以，开展型煤峰值强度后渗透特性研究很有现实意义，在探索出峰后强度渗透率演化的基础上，结合其他瓦斯治理措施，进行全方位的瓦斯治理，才能更好的解决瓦斯超限和局部瓦斯积聚的问题。

1　试验过程

1.1　型煤制备及试验系统

本实验所采集煤样为郑煤集团大坪矿煤，按照标准制作成尺寸为Φ50 mm×H100 mm的圆柱标准型煤试件，型煤的制作方法为：将取来的煤样在破碎机中破碎为煤粉，用0.5 mm的筛子过筛，之后将一定比例的煤粉、水搅拌均匀，放在压力机上以200 kN的压力压制30 min后在脱模机上脱模即可。

试验采用渗流模拟-吸附解吸试验装置，仪器采用模块化设计，便于操作、移动和维护。仪器自动化程度高，实时采集压力、温度、流量等数据，自动控制电磁阀、气动阀的工作状态，自动处理渗流曲线和自动出具实验报告。试验装置如图1所示。

图1　煤岩三轴蠕变—渗流试验系统Fig.1　Three-axis creep-seepage test system for coal and rock

1.2　试验原理及方案

设有一横截面积为A，长度为L的岩石，将其夹持于岩心夹持器中，如图2所示，使粘度为μ的流体在压差△P下通过岩心，测得流量Q。实验证明单位时间通过岩心的体积流量Q与压差△P和岩心横截面积A成正比，与岩心的长度L和流体的粘度成反比：

图2　渗透率计算模型Fig.2　Permeability calculation model

(1)

这就是所谓的“达西方程”，从式中看出A、L是岩石的几何尺寸，△P是外部条件，当外部条件、几何尺寸、流体性质都一定时，流体通过量Q的大小就取决于反映岩石可渗性的比例常数K的大小，我们把K称为岩石的渗透率；式(1)可改写成为：

(2)

此式便可计算岩石的渗透率。

前面讨论的都是以不可压缩流体(液体)为基础的，我们设计的气体渗透率是以气体作为介质，因为气体是压缩流体，所以达西方程式需要修正才能应用。

众所周知，可压缩的气体最大特点是当压力增加流体能被压缩；当压力降低时，流体就发生膨胀；当温度一定时，流体的膨胀服从玻义尔定律。如果以最简单的平面线渗流考虑，设进口压力为P1，出口压力为P2。显然，当压力从P1变化到P2时，气体的体积必然变化，故流速也变化。因此，必须考虑用平均体积流量Q代入达西方程。

若把气体膨胀视为等温过程，按玻义尔定律：

(3)

(4)

(5)

从上面分析得出对可压缩流体的达西公式的修正只把流量用平均流量代入即可：

(6)

式中：μg为气体的粘度。

本试验所采用的试验方案为：测定瓦斯压力为0.7 MPa时，围压分别为2，3，4 MPa条件下加载轴压至煤样破坏后卸载轴压、围压过程中渗透率的变化，以及卸载完成后加载至二次破坏过程中的渗透率的变化特性，以用来模拟煤矿开采过程中煤层所受应力的反复增加与降低。

2　试验结果分析

煤样破坏后测定卸载过程中，以及给予一定的围压加载轴压煤样发生二次破坏过程中渗透率的变化，A1在煤样瓦斯压力为0.7 MPa，围压为2 MPa条件下，加载至煤样破坏后，测定卸载围压、轴压过程中，以及测定围压为1 MPa加载轴压至煤样发生二次破坏过程中的瓦斯流量变化，得出以下曲线，见图3。

图3　A1煤样峰后卸压及二次破坏过程渗透率变化曲线Fig.3　Permeability change curve of A1 coal sample after stress peak unloading and secondary damage process

由图3(a)可知，A1煤样破坏后围压保持2 MPa不变，以20 N/S的速率卸载轴压，应力由12～1 MPa，在此过程中随着轴压的减小，煤样的裂隙逐渐扩张，同时渗透率逐渐增大。轴向应力降至1 MPa时渗透率增加到约1.075 mD，较卸载前增加了约1.3倍。

由图3(b)可知，煤样轴压卸载至1 MPa后，开始卸载围压，煤样产生的裂隙失去围压约束开始松弛，其渗透率逐渐增大，围压卸载至1 MPa后渗透率增加到约1.14 mD比卸载之前增大了约1.32倍。

由图3(c)可知，煤样破坏后随着轴向压力的增大，其裂隙被压缩此时渗透率逐渐减少，轴压增大到一定程度时煤样发生二次破坏，裂隙逐渐扩展渗透率又开始逐渐增大，整个过程中渗透率变化近似U型，A1煤样初次破坏后开始卸载轴压时的渗透率约为0.85 mD，而二次破坏过程中的渗透率极小值约为1.05 mD，可见煤样发生二次破坏过程中其渗透率整体增大，这是由于煤体中已有裂隙通道的存在，二次破坏过程中该裂隙通道先闭合后又发展新的裂隙通道。

A2在煤样瓦斯压力为0.7 MPa，围压为3 MPa条件下，加载至煤样破坏后测定卸载围压、轴压过程中，以及测定围压为2 MPa加载轴压至煤样发生二次破坏过程中的瓦斯流量变化，得出以下曲线，见图4。

图4　A2煤样峰后卸压及二次破坏过程渗透率变化曲线Fig.4　Permeability change curve of A2 coal sample after stress peak unloading and secondary damage process

由图4(a)可知煤样加载至峰值应力破坏之后卸载轴向应力由15 MPa至1 MPa过程中其渗透率逐渐增大，增大速率先缓后快，其渗透率比围压2 MPa条件下有所降低，原因为围压增大，使煤样增密从而减小了其渗透特性，轴向应力降低至1MPa后渗透率增加到约0.9 mD，增大了约1.8倍。

由图4(b)可知当A2煤样轴向应力卸载至1 MPa时开始卸载围压由3～1 MPa，在此过程中煤样横向约束力减小，其破坏后产生的裂隙开始扩张渗透率呈近似线性增长，围压卸载完成后渗透率增加到约1.15 mD，较卸载之前增大了约1.32倍。

由图4(c)可知当A2煤样围压和轴向应力均降为1 MPa后，增大A2煤样的围压至2 MPa，在此过程中煤样的破坏裂隙又重新闭合其渗透率呈近似线性减小，围压增加1 MPa其渗透率减小了约1.17倍。

由图4(d)可知当A2煤样围压加到2MPa时开始增大其轴向应力，当轴向应力约为9 MPa时煤样发生二次破坏，A2煤样初次破坏峰值强度是二次破坏峰值强度的2.33倍。整个过程中A2煤样的渗透率先减小后增大，原因为在初始加压时A2煤样的破坏裂隙发生闭合致密，渗透率在此阶段逐渐减小，当加载轴向应力约为9 MPa时，煤样发生二次破坏，产生新的裂隙，此时渗透率又开始增大，整个过程渗透率变化趋势先减后增近似U型。

对比图4(a)可知A2煤样初次破坏后卸载轴压时的渗透率约为0.48 mD，而A2煤样二次破坏过程中的渗透率极小值约为0.53 mD，由此可见A2煤样二次破坏过程中的渗透率整体要大于初次破坏过程中的渗透率。

A3煤样瓦斯压力为0.7 MPa，围压为4 MPa，加载至煤样破坏后测定卸载围压、轴压过程中，以及定围压为3 MPa加载轴压至煤样发生二次破坏过程中的瓦斯流量变化，得出以下曲线，见图5。

由图5(a)可知A3煤样在围压为4 MPa的条件下轴向应力加载至20 MPa后发生破坏，在卸载轴向应力由20 MPa至1 MPa的过程中其破坏裂隙逐渐扩张，A3煤样的渗透率逐渐增大，当轴向应力降为1 MPa时渗透率增大了约1.3倍。

由图5(b)可知当A3煤样轴向应力卸载到1 MPa时开始卸载其围压由4～1 MPa，在此过程中A3煤样破坏后产生的裂隙约束力减小，裂隙略微扩张，其渗透率逐渐增大，当围压降为1MPa时渗透率增大了约1.25倍。

由图5(c)可知当A3煤样围压和轴向应力均降为1 MPa后，增大A3煤样的围压至3 MPa，在此过程中煤样的破坏裂隙又重新闭合，瓦斯渗流通道变小，气体通过煤样的渗流阻力增大，其渗透率呈近似线性减小，围压增加2 MPa其渗透率减小了约1.22倍。

由图5(d)可知当A3煤样围压加到3 MPa时开始增大其轴向应力，当轴向应力约为13 MPa时煤样发生二次破坏，A3煤样初次破坏峰值强度是二次破坏峰值强度的1.76倍。整个过程中A3煤样的渗透率先减小后增大，原因是在初始加压时A3煤样的破坏裂隙发生闭合致密，渗透率在此阶段逐渐减小，当加载轴向应力约为13 MPa时，煤样发生二次破坏，产生新的裂隙，此时渗透率又开始增大。

图5　A3煤样峰后卸压及二次破坏过程渗透率变化曲线Fig.5　Permeability change curve of A3 coal sample after stress peak unloading and secondary damage process

对比图5(a)可知A3煤样初次破坏后卸载轴压时的渗透率约为0.64 mD，而A3煤样二次破坏过程中的渗透率极小值约为0.62 mD，由此可见，A3煤样二次破坏过程中的渗透率整体要大于初次破坏过程中的渗透率，同A1，A2煤样二次破坏过程中与初次破坏的渗透率对比相一致。

将得到的各煤样数据进行统计得到表1。

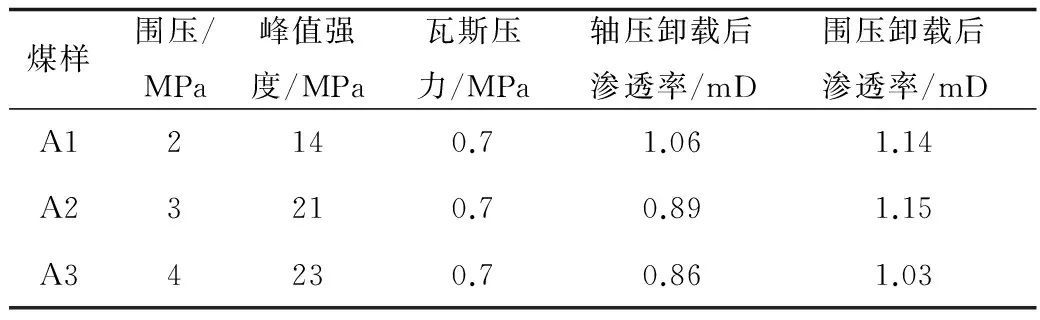
表1　煤样试验结果Table 1　The result of the coal sample experiment

3　结论

1)煤样峰值强度后的渗透率较初始状态有所增大，峰值强度后开始卸载围压和轴压由于在此过程中破坏产生的裂隙失去力的作用，裂隙张开一定程度，其渗透率均增大，其后，给煤样固定一个围压加载轴压使煤样发生二次破坏，此过程中煤样的裂隙先闭合到二次破坏时出现新的裂隙，渗透率先减后增整体呈U型趋势。

2)煤样发生二次破坏过程中的渗透率整体上要大于初次破坏过程中的渗透率。

3)当煤样应力降至1 MPa时渗透率随着围压的增大而呈现减小的趋势，产生该现象的原因在于围压的增大使煤样围向约束加大，从而使煤样中的裂隙通道张开度减小，瓦斯在裂隙中的流动阻力增大。

[1]林柏泉.矿井瓦斯防治理论与技术[M].徐州：中国矿业大学出版社,2010.

[2]Harpalani, S Gas flow through stressed coal [D]. University of California Berkeley,1985.

[3]Gawuga J. Flow of gas through stressed carboniferous strata [D]. University of Nottingham,1979.

[4]Khodot, V V Role of Methane in the stress state of a coal seam[J]. Fiziko-Tekhnicheskie Problemy Razrabotki poleznykh iskopaemykh, 1980(5).

[5]J.R.E.Enever,A.Henning,The Relationship Between Permeability and Effective Stress for Australian Coal and Its Implications with Respect to Coalbed Methane Exploration and Reservoir Modelling[C].Proceedings of the 1997 International Coalbed Methane Symposium.

[6]林柏泉，周世宁.煤样瓦斯渗透率的实验研究[J].中国矿业学院学报，1987,16(1): 21-28 .

LIN Baiquan, ZHOU Shining.Experimental study on gas permeability of coal samples [J]. Journal of China University of Mining and Technology, 1987,16 (1): 21-28.

[7]仵应卿.裂隙岩体应力与渗流关系研究[J].水文地质工程地质,1995,12(2):30-35.

WU Yingqing. Study on the relationship between stress and seepage in fractured rock masses [J]. Hydrogeology and Engineering Geology, 1995,12 (2): 30-35.

[8]李树刚，钱鸣高，石平五.煤样全应力应变中的渗透系数-应变方程[J].煤田地质与勘探，2001，29(1): 22-24.

LI Shugang, QIAN Minggao, SHI Pingwu. Permeability coefficient-strain equation in full stress strain1[J]. Coal Geology and Exploration, 2001,29 (1): 22-24.

[9]李树刚，林海飞，成连华.综放开采支承压力与卸压与瓦斯运移关系研究[J].岩石力学与工程学报，2004, 23(21).

LI Shugang, LIN Haifei, CHENG Lianhua.Study on the relationship between bearing pressure and pressure relief and gas migration in fully mechanized top coal caving mining [J]. Journal of Rock Mechanics and Engineering, 2004, 23 (21).

[10]ZHAO Yangsheng. New advances of block-fractured medium rock fluid mechanics[A].Proceedings engineering. of Im .Symp.On coupled Phenomenain civil mining&Petroleum Sanya, Hainan, China. Nov. 1999.

[11]郭军杰，程晓阳. 循环载荷下煤样渗透特性试验研究[J].中国安全生产科学技术，2017, 13(6).

GUO Junjie, CHENG Xiaoyang.Experimental study on permeability of coal samples under cyclic loading [J].Journal of Safety Science and Technology, 2017, 13(6).

[12]Tang, C.A., Yang, T.H., Tham, L.G., Lee, P.K.K. & Li, L.C. Coupled Analysis of Flow, Stress and Damage (FSD) in Rock Failure[J]. Int. J. Rock Mech. Min. Sci., 2002, 39(4):477-489

[13]刘先珊，林耀生，孔建. 考虑卸荷作用的裂隙岩体渗流应力耦合研究[J]. 岩土力学,2007(S1):192-196.

LIU Xianshan, LIN Yaosheng, KONG Jian.Study on seepage stress coupling of fractured rock mass considering unloading [J]. Rock and Soil Mechanics, 2007(S1): 192-196.

[14]许江，叶桂兵. 长期荷载作用下煤层渗透率演化规律的试验分析[J]. 重庆大学学报,2013(9):1-7.

XU Jiang, YE Guibing.Experimental analysis of coal seam permeability evolution under long term load [J]. Journal of Chongqing University, 2013(9): 1-7.

[15]袁欣鹏，梁冰. 卸压煤层瓦斯抽采渗透率演化模型研究[J]. 中国安全科学学报,2016(2):127-131.

YUAN Xinpeng, LIANG Bing.Study on evolution model of gas extraction permeability in pressure-relieved coal seam [J]. Journal of Chinese Society for Safety Science, 2016(2): 127-131.