基于贝叶斯网络的气井井筒完整性风险评价*

张　弘，申瑞臣，袁光杰，胡耀方

(1. 中国石油集团钻井工程技术研究院，北京 102206；2. 中国石油勘探开发研究院，北京 100083)

0　引言

井筒完整性失效是高压气井、地下储气库注采井生产中面临的主要风险，井筒完整性失效带来巨大的安全隐患。因井口装置泄漏、管材腐蚀、管柱密封失效、井下工具密封失效、固井质量差、圈闭密封失效、盐岩蠕变等风险因素导致气体进入环空，引起环空持续压力，一旦大范围泄漏，危害人员、环境及设备安全。据统计，板桥储气库群76口气井中74口井、金坛盐穴5口老腔及相国寺储气库均存在油套环空、套管环空异常带压的现象，致使修井率提高，维护成本上升[1]。在板桥储气库群46次修井作业中，因管柱相互窜通、环空带压及漏气、安全阀故障、封隔器密封不严等造成修井30次，平均免修期约6 a左右，远低于10 a的例行检测周期。为此，需识别气井井筒完整性的主要风险因素，进行风险分析和风险评价，为井筒完整性失效的早期预防和先期治理提供决策与管理依据。

井筒完整性风险评价，需要分析井筒内压力控制系统的每个节点，识别可能引起各节点失效的潜在因素，明确这些风险因素可能引起的破坏形式、失效事件发生的概率和产生后果的严重程度，并建立风险优先级标准[2-3]。井筒完整性风险涉及井筒全生命周期，需要针对建井、生产、报废各阶段的工况条件，进行完整性失效风险的识别、分析与管理。

目前，国内外学者对油气钻井、生产中的井筒完整性风险评价进行了大量研究，建立了以层次分析法为基础的风险评价模型[4-6]。虞维超等[7]根据系统可靠性理论建立了井筒设备的可靠度模型；Abimbola M等[8-9]采用风险矩阵法进行井筒完整性失效风险评价并将系统安全分析方法应用于钻完井中的井筒完整性风险评价，包括故障树分析、事件树分析和蝴蝶结(Bow-tie)。这些评价模型中对于风险发生概率多通过定性描述进行打分赋值确定，主观性较强，未能实现风险概率的准确量化；Pearl提出用贝叶斯网络表达随机变量之间的因果关联关系，可实现从不完全和不确定的信息中学习与推理，是不确定分析领域最有效的理论模型之一。贝叶斯网络广泛应用于表达和分析不确定性事件，如事故原因分析、项目风险评估、管道失效概率等[10-12]。目前，应用贝叶斯网络进行风险分析过程中，节点先验概率、条件概率的确定主要依赖于专家知识或者大量完整的统计数据集，而在井筒完整性风险评估中，大多数区块并未建立完备的风险案例库。采用Noisy-OR gate模型可以简化条件概率的计算。已知网络结构和一定专家知识情况下通过Noisy-OR gate模型可近似确定贝叶斯网络的条件概率参数。

以下基于贝叶斯网络和Noisy-OR gate模型确定了风险评价要素，建立了气井井筒完整性失效概率的计算方法，与层次分析法相结合明确了风险评价指标，实现了井筒完整性失效风险的定量预测与诊断。

1　贝叶斯网络与Noisy-OR gate模型

1.1　贝叶斯网络基本原理

贝叶斯网络是1种信度网络，采用具有网络结构的有向无环图 (Directed Acyclic Graph) 来表达各个信息要素之间的关联及相互影响程度[11]。可用二元组B=(G,P)表示，其中，G表示具有n个节点的有向无环图，包括节点集A(随机变量)和连接节点之间的有向弧(节点间的关系)，P表示节点相关的条件概率表(CPT)，表示各节点间的相互影响程度。贝叶斯公式是贝叶斯网络的数学基础，对于根节点A1的概率分布用先验概率表示，记为P(A1)，为边缘分布函数；其他节点Ai用条件概率表示，记为P(Ai|π(Ai))，为条件概率分布函数，其中π(Ai)为Ai的父节点集合。

根据变量之间的条件独立性可将包含n个变量的联合概率分布P(A1,A2, …,An)表示为：

(1)

从而简化了联合概率分布计算，降低了模型和推理运算的复杂度。如果节点均为二值离散变量，则对于有n个父节点的子节点，构建该节点的条件概率表需要已知2n项的条件概率和先验概率值。

贝叶斯网络具有在有限、不完整及不确定的节点信息条件下进行学习和推理的能力，从而建立节点关联网络模型。贝叶斯网络的学习分为网络结构学习(构建贝叶斯网络)和参数学习(条件概率表)。常用的结构学习算法有K2算法、爬山算法、结构化的期望最大(SEM)算法等。关于贝叶斯网络的参数学习方法，完整数据模式下有最大似然估计法(MLE)，缺少数据情况下可采用期望最大(EM)法。贝叶斯网络推理是指根据建立的贝叶斯网络结构及条件概率表，在给定证据后计算某些节点取值的概率。可分为正向推理(由因及果)和反向推理(由果溯因)。推理算法主要有多树传播算法、联结树算法、随机抽样算法和消息循环传递算法等。

在先验概率条件下，基于贝叶斯网络预测其他节点发生的概率，可用于计算井筒完整性失效概率。同时可反向推理井筒完整性失效的主要风险因素。

1.2　Noisy-OR gate模型

应用Noisy-OR gate模型的前提假设条件[9]包括：各个变量因素相互独立，每个变量导致的后果不会受到其他变量的相互影响；每个变量单独作用都可以造成这种共同结果，至少有1个变量为真值时才会导致该结果的发生。

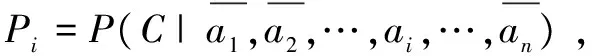
对于如图1(a) 所示的贝叶斯网络，节点A3是节点A2和A4的子节点，根据Noisy-OR gate模型假设可以得出节点A3的4种条件概率的表达形式。

则有：

图1　Noisy-OR gate模型示例Fig.1　Examples of Noisy-OR gate model

如图1(b)所示，对于由n个双值变量组成的父节点的Noisy-OR gate模型，则由节点A1,A2,…,An，记为集合A，确定的子集Asub取真值导致C发生的条件概率为：

(2)

实际分析中影响C的风险因素除集合A外还存在另外一些未能有效识别的未知因素，在此需要使用Noisy-OR gate的扩展模型Leaky Noisy-OR gate，将所有未能有效识别的风险因素归结为1个因素AL，其连接概率为遗漏概率(Leaky Probability)，记为PL。

根据式(2)，采用Leaky Noisy-OR gate模型结果节点C发生的条件概率为：

(3)

另外，Leaky Noisy-OR gate模型还可用于确定父节点的连接概率。节点C还可看作具有2个父节点的子节点。即A中某一风险因素Ai和除Ai外其他所有风险因素集Aa，Aa总能导致C发生，Aa总为真值。相应的这2种因素的连接概率为Pi和Pa。则由式(2)得：

(4)

则由(4)式可得到连接概率Pi为：

(5)

由式(5)可计算出子节点C的全部父节点连接概率P1，…，Pi，…，Pn，由式(3)可确定条件概率表。只需要已知2n项即可计算该节点的条件概率表。

2　贝叶斯网络风险评价模型的建立

2.1　贝叶斯网络的构建

贝叶斯网络的根节点即为影响井筒完整性的风险因素，有效识别风险因素是评估风险的第一步。井筒完整性分析应分别考虑井屏障单元的失效，包括井筒的实体屏障和水力屏障。结合挪威石油工业协会(OLF) 117标准《油气井完整性推荐做法指南》[13]定义的井屏障组件及气井环空带压原因分析[14]，本文将井筒分为管柱、水泥环、井口、其他部件和水力屏障5个评价单元，其中管柱包括完井管柱和套管柱，失效形式包括管体破损和丝扣密封失效；其他部件包括井下安全阀、封隔器等；水力屏障包括油套环空保护液和环空中水泥上方的液柱压力。

根据专家知识与现场实践，提取出井筒完整性失效风险因素包括但不限于以下因素[15-16]：

1)管柱的腐蚀破坏

套管和油管柱受地层水，CO2，H2S等酸性气体的影响，发生强度下降与腐蚀破坏，与地层流体性质、酸气含量与分压，温度等因素有关。

2)管柱强度不足

由于管体或螺纹设计强度不足、安全系数小于标准或管柱存在原始缺陷，导致作业中套管柱、完井管柱受到外挤、内压、拉断和剪切破坏。

3)密封性缺陷

包括管柱的丝扣、管体本身密封缺陷、水泥环胶结面、井口及管柱附件如封隔器、井下安全阀、悬挂器等单元的密封性失效，造成流体泄漏或窜流。

4)地质构造因素导致套管损坏，包括地层压实，膏岩蠕变，地层滑移等因素。

5)井口、采气树等装置的功能失效。

6)环空保护液漏失导致水力屏障失效。

根据以上单元划分及风险因素类型，井筒完整性风险分布如图2所示。

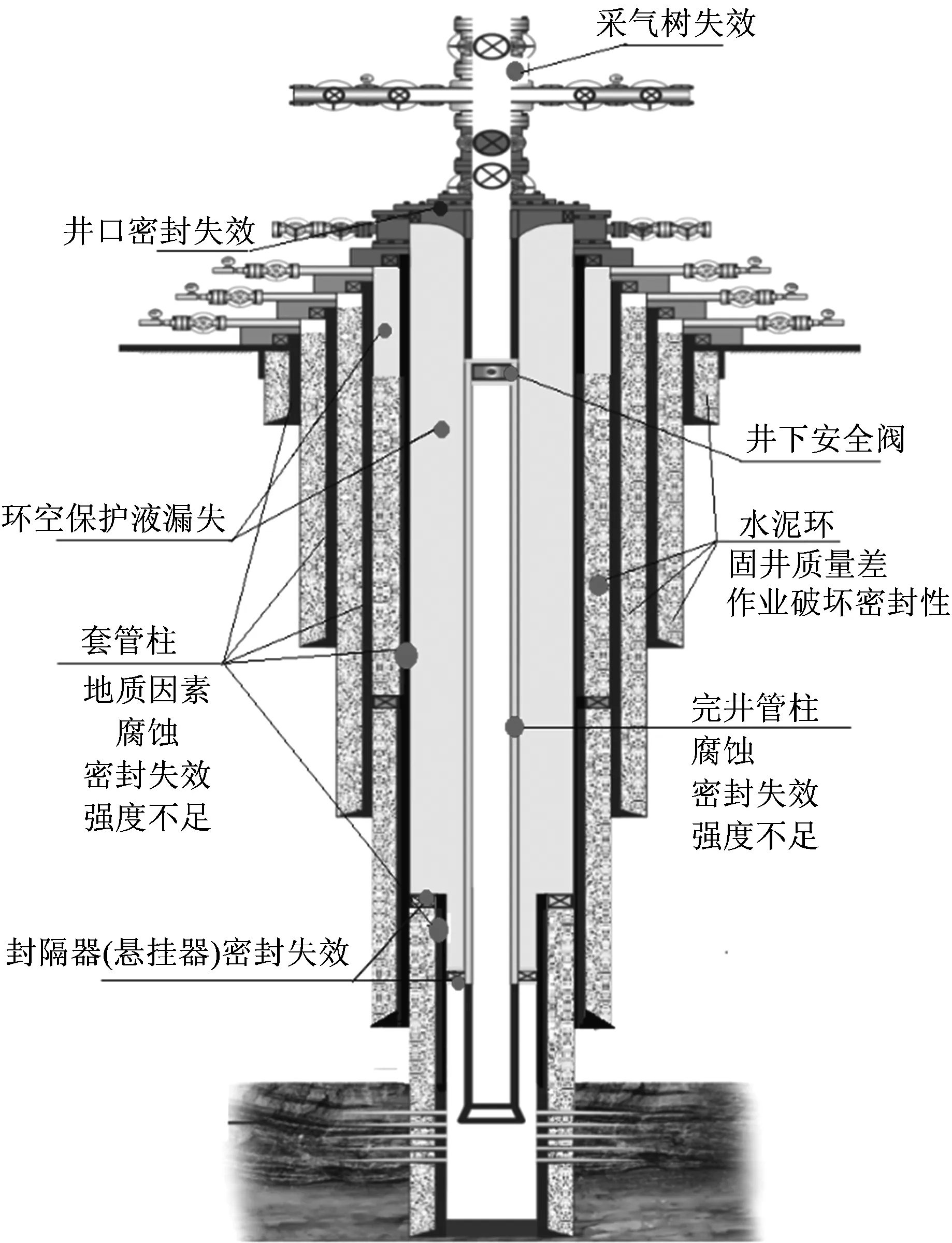
图2　气井井筒完整性风险分布Fig.2　Risk distribution threatening well integrity

由图2风险因素分布与井筒单元划分，结合专家知识，采用故障树分析井筒完整性失效单元及风险因素之间的因果关系，如图3所示。

根据故障树示意图与贝叶斯网络的映射关系，将事件与节点对应，基本事件为贝叶斯网络的根节点，顶层事件作为叶节点；将逻辑门与条件概率建立映射。以此为依据建立井筒完整性失效的贝叶斯网络如图4所示。

2.2　贝叶斯网络的参数学习

图3中的贝叶斯网络节点均为二值变量，其值域只有真值(1)和假值(0)2种状态，这些节点及其父节点所组成的局部贝叶斯网络满足Noisy-OR gate模型的使用条件，其条件概率参数可以通过Leaky Noisy-OR gate方法近似计算。根节点的条件概率可通过历史数据推断，对于历史故障数据较少的因素，可通过专家知识赋予相对主观的条件概率值。

图3　井筒完整性失效故障树Fig.3　Fault tree analysis for well integrity failure

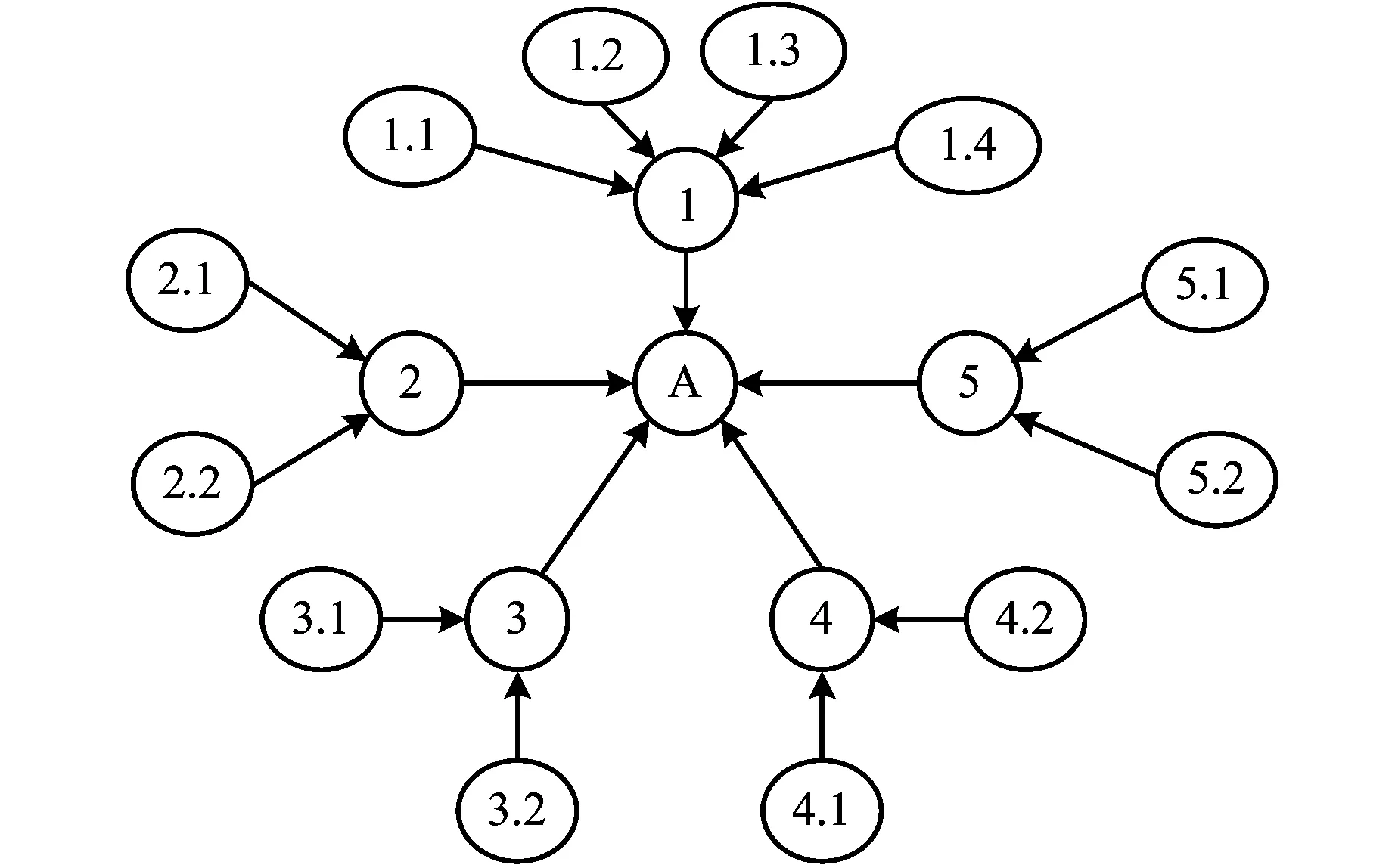
A—井筒完整性失效；1—管柱失效；2—水泥环密封失效；3—井口装置失效；4—水力屏障失效；5—其他部件失效；1.1—腐蚀环境；1.2—管柱强度不足；1.3—管柱螺纹密封性差；1.4—可能导致套管损坏的地质因素；2.1—固井质量差；2.2—作业中可能导致水泥环密封性损坏的因素；3.1—采气树损坏；3.2—井口密封性失效；4.1—油套环空保护液漏失；4.2—水泥上方保护液漏失；5.1—封隔器密封失效；5.2—井下安全阀失效图4　井筒完整性风险评估的贝叶斯网络模型Fig.4　Bayesian Network for risk evaluation of well integrity

例如，据统计某油田100口高压气井中，在一定时期内共有40口井发生套损及完井管柱失效，有60口井存在较强腐蚀环境，其中的24口井的套管柱及完井管柱发生腐蚀损坏，则可以得到条件概率P(A1=1|A1.1=1)=0.6，P(A1=1|A1.1=0)=0.4。

根据统计数据集，对于节点A1存在如下已知概率：P(A1=1|A1.1=1)=0.60，P(A1=1|A1.2=1)=0.64，P(A1=1|A1.3=1)=0.72，P(A1=1|A1.4=1)=0.56，P(A1=1|A1.1=0)=0.40，P(A1=1|A1.2=0)=0.34，P(A1=1|A1.3=0)=0.30，P(A1=1|A1.4=0)=0.12。则由式(5)计算A1.1，A1.2，A1.3和A1.4的连接概率分别为0.33，0.45，0.60和0.50。设该节点的遗漏因素的连接概率为PL=0.05，由式(3)计算节点A1的条件概率见表1。

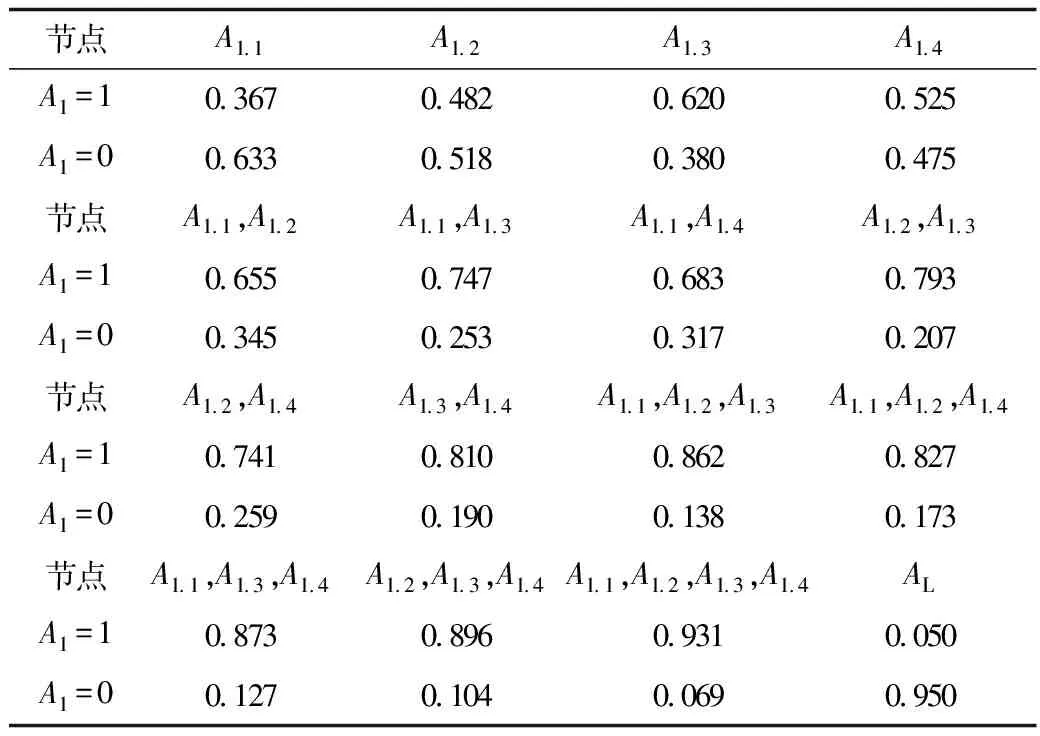
表1　管柱失效A1的条件概率

上表中的父节点为该节点取真值时子节点取真值或假值的概率。

对于节点A2由已知概率：P(A2=1|A2.1=1)=0.80，P(A2=1|A2.2=1)=0.64，P(A2=1|A2.1=0)=0.36，P(A2=1|A2.2=0)=0.24，计算出A2.1和A2.2的连接概率分别为0.69和0.53。取遗漏概率为0.05，水泥环密封失效的条件概率，见表2。

表2　水泥环密封失效A2的条件概率

对于井口装置失效、水力屏障失效和其他部件失效，图4中父节点为真时一定导致这些节点为真，因此这3个节点的父节点的连接概率均为1，A3，A4，A5的遗漏概率分别取0，0.05和0.1。另外，任一节点A1，A2，A3，A4和A5发生时都会导致A为真，取PL=0.05，可确定井筒完整性失效节点A的条件概率参数。

根据以上节点的条件概率，利用贝叶斯网络的消息传递可计算井筒完整性失效的后验概率。

2.3　井筒完整性风险指标与等级

在某一特定环境、时间段内，某种损失发生的可能性即为风险，在此借鉴层次分析法评价井筒完整性的指标构建原理建立风险指标和风险等级标准。某一风险因素的风险值为Li=Pi×Ci，其中，Pi为该风险的发生概率，Ci为可能产生的后果的严重程度。将井筒完整性各风险单元失效的风险严重度分为5级并对各单元的严重度量化赋值[8]，见表3。

表3　风险单元失效的后果严重程度

根据前文贝叶斯网络模型得到的管柱、水泥环、井口装置、水力屏障和其他部件失效风险的发生概率值和严重度，定义风险度作为井筒完整性风险评价指标[6]。风险度定义为：

(6)

式中：R为井筒完整性风险度，wi为该风险因素的权重。

风险因素的相对权重可通过构造判断矩阵计算特征向量求出，详细求解原理见文献[5]，如对于图4中1～5节点，构造判断矩阵为：

A=

该判断矩阵满足一致性要求，归一化权重为w=(0.401 0, 0.283 4, 0.105 7, 0.068 3, 0.141 7)T。

由于存在遗漏概率，失效概率取值范围为(0～1)的子区间，在以上严重度、权重取值范围条件下，风险度区间为(4.62～80.73)，为便于使用，将风险度折算至(0～100)范围。根据相关标准及专家意见，将井筒完整性风险按照风险度分为4个风险优先级，并以此来制定相应的技术与管理对策，见表4。

表4　气井井筒完整性风险等级

3　风险评估与分析

采用匹兹堡大学开发的开放式贝叶斯网络模拟软件GeNIe 2.0进行随机变量运算，采用Poly-Tree算法进行网络推理。根据建立的贝叶斯网络结构和由Noisy-OR gate模型确定的节点条件概率表，评估井筒完整性失效风险。根节点各因素发生的概率，为先验概率，可通过某区块气井的历史资料推断或结合专家知识对图4中基本事件(根节点)的发生概率赋值，先验概率值及计算结果见图5。

图5　贝叶斯网络井筒完整性失效概率分布Fig.5　Probability distribution of well integrity failure through Bayesian Network

可知，在该先验概率条件下，气井井筒完整性失效的风险概率为75.8%。该井管柱、水泥环、井口装置、水力屏障和其他部件的风险概率分别为46.1%，23.8%，9.8%，15.4%和18.8%，根据风险度定义计算得该井的风险度为R=30.77，由表4可知该井属于Ⅱ级中度风险井，尽管井筒完整性失效的概率较高，但总体风险较低。

另外，由各单元的风险概率值可知该井的薄弱环节为管柱和水泥环密封性，特别应注意防腐和地质因素对套管的损坏。在生产过程中应监测环空压力并有针对性地制定防控措施。

由贝叶斯网络还可以确定井筒完整性失效的最大可能致因链。设定井筒完整性失效概率为100%，通过贝叶斯网络反向推理各根节点变量的概率值，从而确定影响井筒完整性的主要风险因素，见图6。

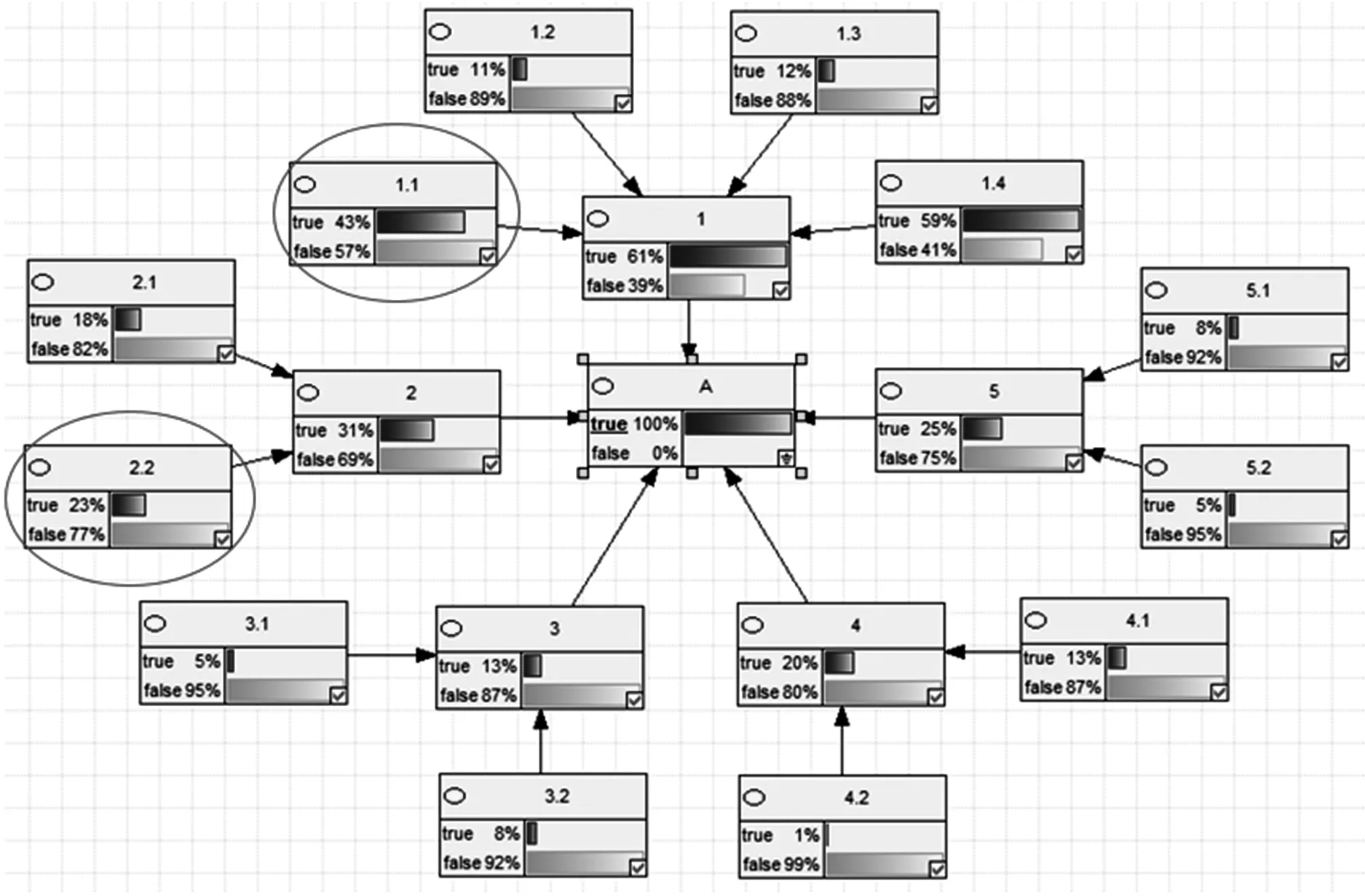
图6　贝叶斯网络井筒完整性风险因素分析Fig.6　Analysis of risk factors of well integrity by Bayesian Network

可知，在该条件概率参数下，造成井筒完整性失效的主要原因为地质因素引起的套管柱的损坏和强腐蚀环境造成管柱的腐蚀破坏，因此应注意管柱的防腐和套管的优化设计。

4　结论

1)根据影响气井井筒完整性的因素，将井筒划分为管柱、水泥环、井口装置、水力屏障和其他部件5个评价单元；通过故障树分析，建立了井筒完整性失效的贝叶斯网络结构；通过Noisy-OR gate模型确定节点的条件概率表，减少了对样本数据的需求数量；建立了气井井筒完整性失效概率的贝叶斯网络模型，实现了失效概率的定量计算；或反向推理得到高风险因素，确定主要致因因素。

2)将贝叶斯网络模型确定的风险概率与层次分析法结合，引入井筒完整性的风险评价指标和风险等级划分，建立了气井井筒完整性风险评价方法，实现了井筒完整性风险的定量评价。该方法有助于降低气井井筒完整性的风险，可为制定有效的防控技术对策提供依据。

[1]丁国生，李春，王皆明，等．中国地下储气库现状及技术发展方向[J]．天然气工业，2015，35(11)：107-112．

DING Guosheng, LI Chun, WANG Jieming, et al. The status quo and technical development direction of underground gasstorages in China[J]. Natural Gas Industry, 2015, 35(11): 107-112.

[2]李丽锋，罗金恒，赵新伟，等．盐穴地下储气库风险评估技术与控制措施[J]．油气储运，2010，29(9)：648-651．

LI Lifeng, LUO Jinheng, ZHAO Xinwei, et al. Risk assessment technique and control measures of salt cavern underground gas storage[J]. Oil & Gas Storage and Transportation, 2010, 29(9): 648-651.

[3]马英敏．伊朗SP11区块井筒完整性风险评价研究[D]．青岛：中国石油大学(华东)，2013．

[4]储胜利，樊建春，张来斌，等．套管段井筒完整性风险评价方法研究[J]．石油机械，2009，37(6)：1-4．

CHU Shengli, FAN Jianchun, ZHANG Laibin, et al. Research on the risk assessment method for wellbore integrity in casing section[J]. China Petroleum Machinery, 2009, 37(6): 1-4.

[5]李隽，王晓冬，王云，等．基于层次分析法的气井完整性评价模式[J]．钻采工艺，2013，36(3)：31-34．

LI Juan, WANG Xiaodong, WANG Yun, et al. Evaluation mode of the gas well integrity based on analytic hierarchy process (AHP)[J]. Drilling & Production Technology, 2013, 36(3): 31-34.

[6]张智，何雨，王一婷，等．含硫气井井筒完整性风险评价研究[J]．中国安全生产科学技术，2017，13(4)：101-107．

ZHANG Zhi, HE Yu, WANG Yiting, et al. Research on risk evaluation of well integrity for sour gas wells[J]. Journal of Safety Science and Technology, 2017, 13(4): 101-107.

[7]虞维超，薛鲁宁，黄维和，等．储气库可靠性一体化分析方法研究[J]．石油科学通报，2017，2(1)：102-114．

YU Weichao, XUE Luning, HUANG Weihe, et al. An integration method for evaluating the operating reliability of underground natural gas storage[J]. Petroleum Science Bulletin, 2017, 2(1): 102-114.

[8]Dethlefs J C, Chastain B. Assessing well-integrity risk: a qualitative model[J]. SPE Drilling & Completion, 2012, 27(2): 294-302.

[9]Abimbola M, Khan F, Khakzad N. Risk-based safety analysis of well integrity operations[J]. Safety Science, 2016, 84(4):149-160.

[10]阴东玲，陈兆波，曾建潮，等．基于带权重定性贝叶斯网络的煤矿事故人因推理[J]．武汉理工大学学报(信息与管理工程版)，2017，39(1)：10-14．

YIN Dongling, CHEN Zhaobo, ZENG Jianchao, et al. Human factors inference of safety accidents in coal mine based on qualitative Bayesian network with weight[J]. Journal of WUT (Information & Management Engineering), 2017, 39(1): 10-14.

[11]张俊光，徐振超，贾赛可．基于Noisy-or Gate和贝叶斯网络的研发项目风险评估方法[J]．科技管理研究，2015，35(1)：193-196．

ZHANG Junguang, XU Zhenchao, JIA Saike. Risk Assessment on research and development project based on Noisy-OR gate and Bayesian network[J]. Science and Technology Management Research, 2015, 35(1): 193-196.

[12]郝永梅，邢志祥，沈明，等．基于贝叶斯网络的城市燃气管道安全失效概率[J]．油气储运，2012，31(4)：270-273．

HAO Yongmei, XING Zhiming, SHEN Ming, et al. Calculate the failure probability of urban gas pipeline based on Bayesian network model[J]. Oil & Gas Storage and Transportation, 2012, 31(4): 270-273.

[13]Norwegian Oil and Gas Association (prior OLF). 117- OLF Recommended guidelines for well integrity [S]. Stavanger: OLF, 2011.

[14]古小红，母建民，石俊生，等．普光高含硫气井环空带压风险诊断与治理[J]．断块油气田，2013，20(5)：663-666．

GU Xiaohong，MU Jianmin, SHI Junsheng, et al. Diagnosing and managing on risk of annular casing pressure in high-sulfur gas well of Puguang Gas Field[J]. Fault-Block Oil & Gas Field, 2013, 20(5): 663-666.

[15]谢丽华，张宏，李鹤林．枯竭油气藏型地下储气库事故分析及风险识别[J]．天然气工业，2009，29(11)：116-119．

XIE Lihua，ZHANG Hong，LI Helin. Accident analysis and risk identification of underground gas storage rebuilt upon the depleted oil and gas reservoirs[J]. Natural Gas Industry, 2009, 29(11): 116-119.

[16]孙莉，樊建春，孙雨婷，等．气井完整性概念初探及评价指标研究[J]．中国安全生产科学技术，2015，11(10)：79-84．

SUN Li, FAN Jianchun, SUN Yuting, et al. Discussion on concept and evaluation index of gas well integrity[J]. Journal of Safety Science and Technology, 2015, 11(10): 79-84.