考虑峰后软化的圆形巷道稳定性分析及工程应用*

刘怀付，张振全，刘万荣，马海峰

(1. 安徽理工大学 深部煤矿采动响应与灾害防控重点实验室，安徽 淮南 232001；2. 安徽理工大学 能源与安全学院，安徽 淮南 232001；3．中国矿业大学(北京) 资源与安全工程学院，北京 100083)

0　引言

地下巷道开挖后，其附近围岩的应力状态会发生改变，导致巷道变形失稳，严重影响巷道的正常使用。确定准确的巷道塑性区范围、控制巷道变形量和进行巷道围岩应力分析对工程的安全与成本节约具有重要意义。

当前对巷道的弹塑性范围和位移分析，多采用Hoek-Brown[1-2](H-B)准则或Mohr-Coulomb[3-5](M-C)强度准则，忽略中间主应力σ2和峰后强度参数软化的影响，所得塑性范围和位移解结果偏于保守，与实际变形情况相差很大。许多学者合理的考虑了中间主应力的作用，在Drucker-Prager(D-P)屈服准则[6-8]的基础上进行了研究，但D-P屈服准则具有多种形式，基于不同形式的D-P屈服准则的分析结果差距较大，同时公式较繁琐，不利于实际工程中的运用。与其他屈服准则相比，统一强度理论不仅考虑中间主应力的作用，而且形式简单[9]，很好弥补了M-C准则和D-P准则等不足，在巷道围岩弹塑性分析中得到广泛的应用[10-13]。现有围岩弹塑性分析常假定塑性区弹性应变为定值[14]，其大小等于弹塑性交界处弹性区的应变值，不能真实地反映塑性区弹性应变的对围岩塑性区范围和位移的影响，使得塑性区范围和位移偏小，导致工程设计偏危险。当岩石的强度超过其峰值强度后会发生软化，岩体的力学性能会劣化，其强度参数会不同程度地减小[6,15-16]，现有围岩弹塑性分析多数没有考虑这一特性，导致结果与实际不符。

本文基于统一强度理论，考虑峰后软化、中间主应力和塑性区弹性应变的影响，引入软化系数，推导出巷道围岩塑性区半径、位移和弹塑性应力表达式，结合具体算例，分析了相关参数对塑性范围、位移和应力分布的影响，并通过数值模拟和现场实测验证了理论结果的正确性，所得结果可为巷道稳定性分析和支护提供一定的理论指导和建议。

1　理论分析模型

1.1　力学模型

假设巷道断面为圆形，围岩均质、各向同性，巷道深埋且长度足够大。图1为深部圆形巷道力学模型：R0为巷道半径，Rp为巷道塑性软化区半径，支护阻力pi均匀作用在开挖巷道内壁处，初始地应力p0作用在无穷远处。

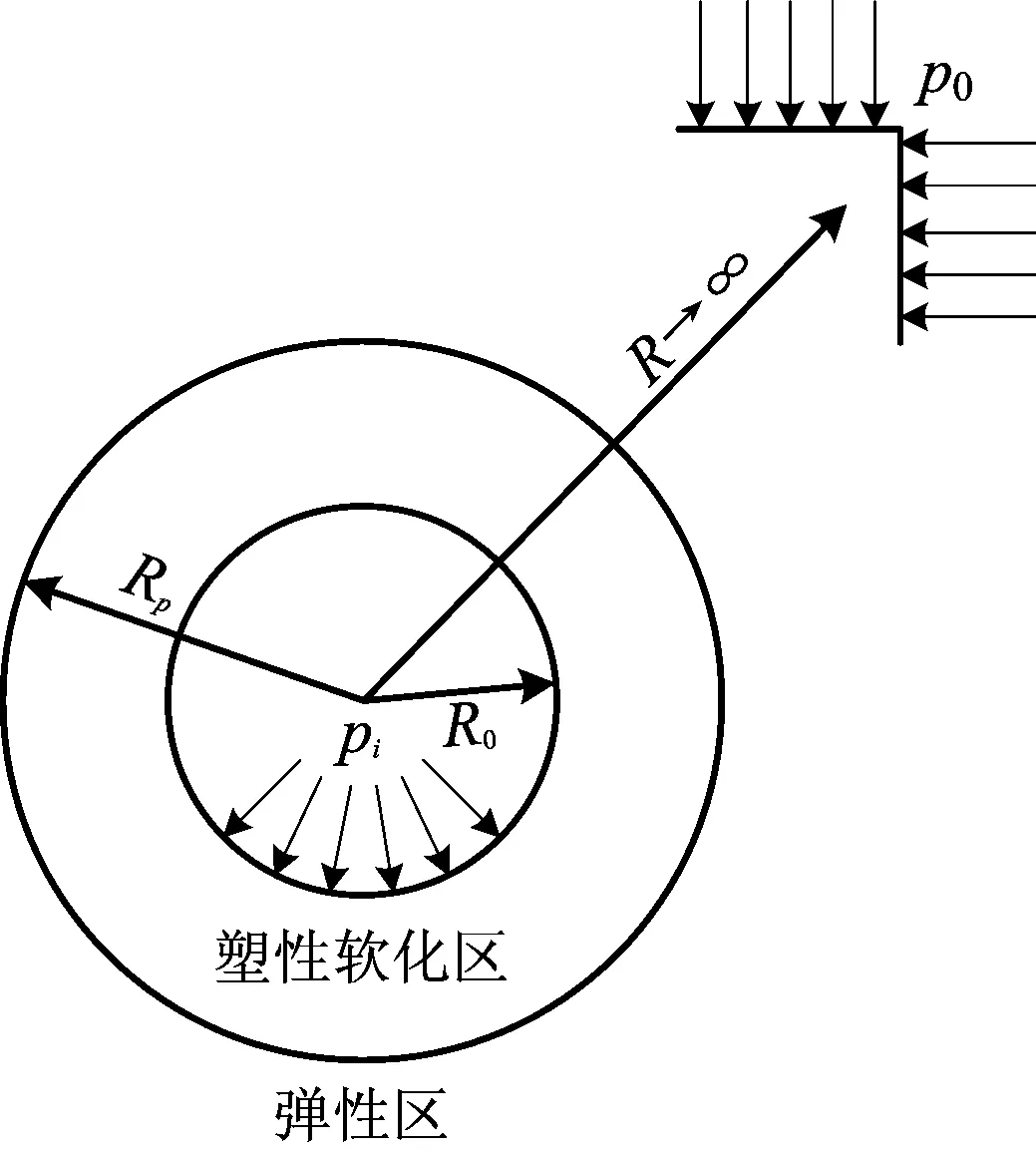
图1　圆形巷道力学模型Fig.1　Mechanical model of circular tunnel

1.2　统一强度准则

σθ=Ajσr+Bj

(1)

(2)

式中:σθ和σr分别为巷道围岩的切向应力和径向应力，MPa；Aj和Bj为岩石强度表征参数，表示最大主应力和最小主应力之间的关系；j为符号参数，j=e表示围岩软化前，对应初始内摩擦角φe和黏聚力ce，j=p表示围岩软化后，对应塑性软化区摩擦角φp和黏聚力cp；b为中间主应力系数，0≤b≤1。

1.3　软化模型

在全应力-应变曲线中，当岩石的强度超过其峰值强度后会发生软化，塑性区内摩擦角φp和黏聚力cp随着塑性应变的增加而逐渐减小，假定φp和cp与初始内摩擦角φe和黏聚力ce成线性软化，引入软化程度系数kφ和kc，有：

(3)

(4)

式中：kφ和kc分别是内摩擦角和黏聚力软化系数；φe和ce是围岩初始内摩擦角和黏聚力；φp和cp为塑性软化区摩擦角和黏聚力，(°)和MPa；φs和cs是残余内摩擦角和残余黏聚力，(°)和MPa；Rp为塑性区半径，m。

2　巷道围岩弹性区和塑性区分析

2.1　弹性区应力场和位移场

巷道围岩处于线弹性状态下，设py为围岩弹性区与塑性软化区交界处径向应力，巷道弹性区视为受py和地应力p0共同作用下的厚壁圆筒，可知弹性区应力和位移为：

(5)

式中：E，μ分别为围岩的弹性模量和泊松比；ue为弹性区位移，m；r为巷道中心到围岩某一点的距离，m。

在弹塑性交界处r=Rp处，式(5)满足式(1)且径向应力连续，整理可得：

(6)

将r=Rp代入式(5)可得弹塑性交界处位移为：

(7)

2.2　塑性区应力场和位移场

围岩中任一研究单元点满足平衡微分方程：

(8)

将式(1)代入式(8)并进行积分，以σr|r = R0=pi为边界条件，可得塑性区径向应力和切向应力为：

(9)

考虑弹塑性交界处径向应力连续，即σrp|r = Rp=σre|r = Rp。联立式(9)第一式和式(5)第一式可得塑性区半径为：

(10)

围岩塑性区的径向应变εr和切向应变εθ可分解为塑性应变和弹性应变，即：

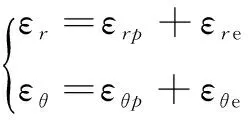
(11)

假设塑性区围岩不可压缩，则塑性应变εrp与εθp的关系为：

εrp+εθp=0

(12)

由式(11)和(12)可得：

εr+εθ=(εrp+εre)+(εθp+εθe)=εre+εθe

(13)

将几何方程εr=du/dr，εθ=u/r带入式(13)得：

(14)

不考虑初始地应力引起的位移，利用广义胡克定律可得塑性区围岩弹性应变为：

(15)

将式(9)，(15)代入式(14)，进行积分并以弹塑性交界r=Rp处的位移为边界条件，将式(7)和(10)代入整理可得巷道塑性区的位移为：

(16)

其中：

(17)

式(16)为考虑塑性软化、塑性区弹性应变和中间主应力的巷道围岩塑性区位移通用表达式。

3　算例分析

以淮南矿区某矿三水平-1 000 m埋深胶带运输机巷道掘进面进行试验，现场实测初始地应力p0=23.3 MPa。巷道断面为为圆形，半径R0=3 m，支护压力pi=2 MPa。根据现场取样实验室测得巷道的围岩力学参数为：围岩的弹性模量E=10 GPa，泊松比μ=0.3，初始内摩擦角φe=30°，残余内摩擦角为φs=10°，初始黏聚力ce=8 MPa，残余黏聚力cs=1 MPa。

3.1　中间主应力系数b对巷道塑性区半径Rp、塑性区位移u和围岩应力分布的影响

如图2，3和4分别为巷道塑性区半径Rp、塑性区位移u和围岩应力分布随中间主应力系数b的变化示意图。由图2可知：在不考虑峰后软化时，随中间主应力系数b的增大，塑性区半径逐渐递减，当b分别为0，0.25，0.5，0.75和1时，巷道塑性区半径Rp分别为6.04，5.60，5.36，4.95和 4.74 m，塑性区半径Rp(相对于b=0)分别减小了7.28%，11.26%，18.05%和21.5%。

图2　kφ=1和kc=1时b与塑性区Rp的关系Fig.2　Relation between b and the plastic zone Rp when kφ=1 and kc=1

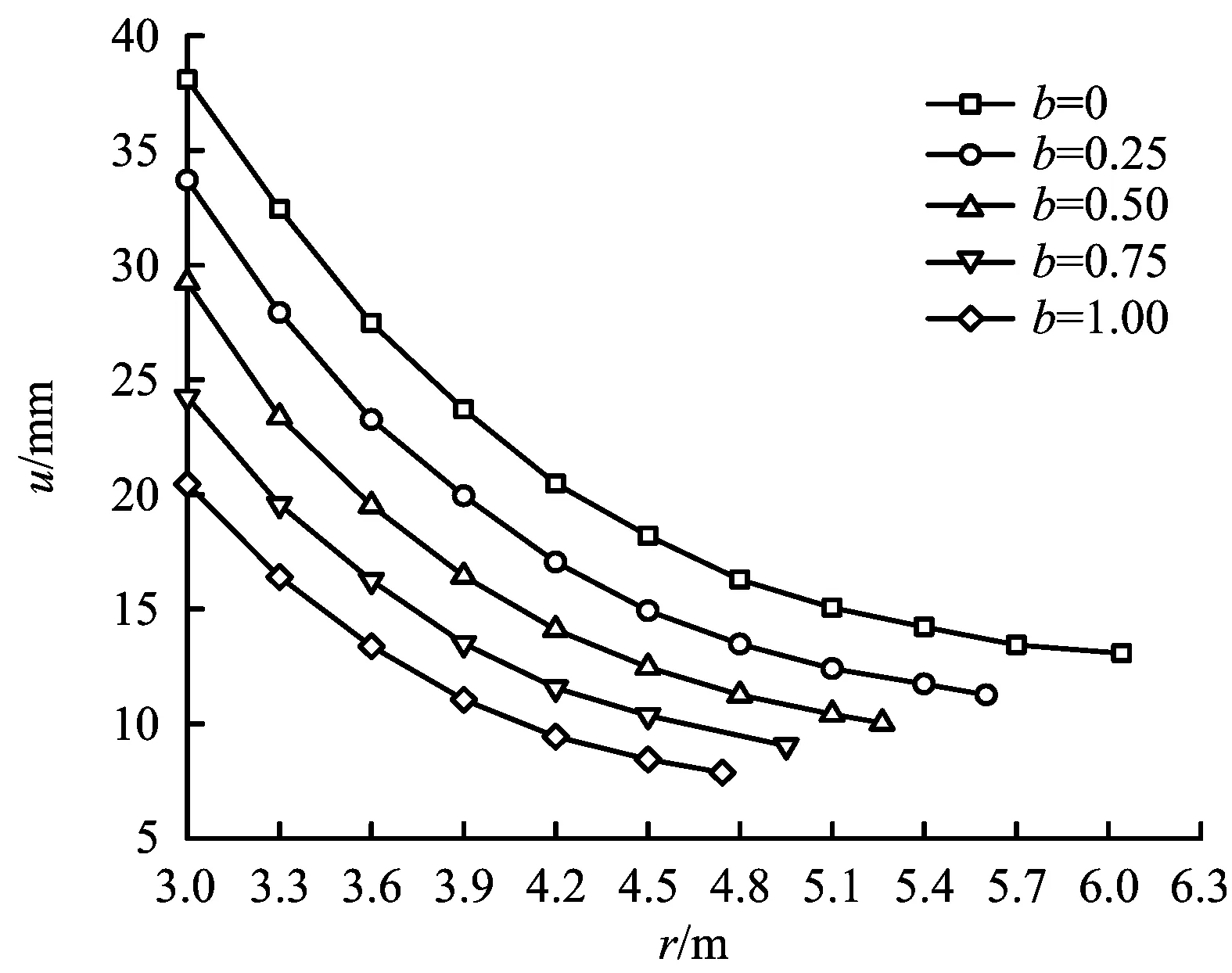
图3　kφ=1和kc=1时b与塑性区位移u的关系Fig.3　Relation between b and the displacement u of plastic zone when kφ=1 and kc=1

图4　kφ=1和kc=1时b与巷道围岩应力分布的关系Fig.4　Relation between b and the stress distributions of roadway surrounding rock when kφ=1 and kc=1

由图3可知：巷道塑性区位移u随着b的增大而逐渐降低，当b分别为0，0.25，0.5，0.75和1时，巷道塑性区内壁处的位移分别为38.10，33.71，29.25，24.24，20.45 mm，相对于不考虑中间主应力的影响(b=0)，巷道洞壁处的位移分别减少了11.52%，23.23%，36.38%和46.3%。

由图4可知：随着b值的增大，塑性区切向应力和围岩径向应力逐渐增大，弹性区切向应力和径向应力逐渐减小，b=1所对应的最大切向应力(56.42 MPa)比b=0所对应的最大切向应力(50.21 MPa)增加了6.21 MPa，围岩的极限强度增加了11.0%。

按照相关规则,按照税法规定外国企业以及外国企业收入,相关企业包含三例:在资金、运营、购销等方面，存在直接或间接地操控或具有联系;直接或间接地同为第三者所操控或具有;以及有其他利益上的相相联系。

综上分析可知：考虑中间主应力能够提高围岩的极限强度，充分发挥围岩自身的承载潜能，当b=0 时，统一强度理论退化成摩尔-库伦准则，应用摩尔-库伦准则求解的围岩极限承载值偏小，塑性区半径偏大，造成与实际结果偏差较大。

3.2　内摩擦角软化系数kφ对巷道塑性区半径Rp和塑性区位移u的影响

图5　b=0.5和kc=1时kφ与Rp的关系Fig.5　Relation between kφ and plastic zone radius Rp when b=0.5 and kc=1

图6　b=0.5和kc=1时kφ与塑性区位移u的关系Fig.6　Relation between kφ and the displacement u of plastic zone when b=0.5 and kc=1

由图6可知：巷道塑性区位移u随着的φj减小而逐渐增大，kφ从1降低到1/6时，巷道洞壁处的位移由29.25 mm增加到42.37 mm，比不考虑内摩擦角软化增大了30.3%。可见考虑峰后内摩擦角软化系数kφ后，巷道塑性区范围和变形会有很大程度的增大，不考虑峰后软化，计算结果会偏于保守。

3.3　黏聚力软化系数kc变化对巷道塑性区半径Rp和塑性区位移u的影响

如图7和8分别为巷道塑性区半径Rp和塑性区位移u随黏聚力软化系数kc的变化示意图。由图7可知：当b=0.5和kφ=1时，随着kc的逐渐递减，塑性区半径Rp逐渐增大，当1/8≤kc≤5/8时，kc对塑性区半径的影响较大，当5/8

图7　b=0.5和kφ=1时kc与Rp的关系Fig.7　Relation between kc and plastic zone radius Rp when b=0.5 and kφ=1

图8　b=0.5和kφ=1时kc与塑性区位移u的关系Fig.8　Relation between kc and the displacement u of plastic zone when b=0.5 and kφ=1

由图8可知：巷道塑性区位移u随着的kc减小而逐渐增大，kc从1降低到1/8时，巷道洞壁处的位移由29.25增加到53.37 mm，比不考虑黏聚力软化增大了42.3%。实际工程中，塑性区围岩会发生塑性软化，在计算时考虑峰后黏聚力的降低，会使结果更准确。

4　数值计算与现场实测

4.1　数值计算

采用Flac3D有限差分程序分析不同软化系数下的围岩响应特征。以淮南矿区某矿三水平-1 000 m埋深胶带运输机巷道工程地质条件为背景，模型尺寸30 m×15 m×15 m(长×宽×高)，圆形巷道断面半径为3 m。鉴于所模拟巷道轴向尺寸远大于其断面半径，计算中选取平面应变模型，其中网格节点100 901个，单元总数为98 400个，计算时采用摩尔库伦准则。考虑到模型的边界效应，根据圣维南原理，模型取足够大的尺寸，并根据所研究巷道周围岩层塑性区半径和位移分布形态，将巷道周围网格加密，向巷道外侧延伸放射状网格。

巷道的围岩力学参数为：围岩的弹性模量E=10 GPa，泊松比μ=0.3，初始内摩擦角φe=30°，残余内摩擦角为φs=10°，初始黏聚力ce=8 MPa，残余黏聚力cs=1 MPa。模型上部施加载荷γh=23.3 MPa，水平方向施加载荷γh=23.3 MPa，底部垂直方向位移约束。为研究方便，只考虑中间主应力系数b=0的情况，统一强度准则变成M-C强度准则。图9和10分别不同软化系数下的巷道围岩塑形区和位移场分布。

图9　塑性区分布Fig.9　Distribution nephogram of plastic zones

图10　位移分布Fig.10　Distribution nephogram of displacement

4.2　现场实测分析

图11　巷道表面位移监测曲线Fig.11　Displacement curves of tailgate during driving

通过图11的3个测点的顶底板和两帮位移移近量变化趋势可知：3个测点在距掘进面0～28 m左右时的顶底板和两帮移近量变化很大，在50 m以后移近量变化趋于缓和，在50 m左右顶底板和两帮移近量最大值分别达到48.92 mm 和42.24 mm，平均为47.65 mm和40.73 mm。在巷道掘进0～120 m的实测过程中，顶底板的最大移近量达到56.42 mm，两帮的最大移近量达到51.25 mm。在短时间内表面位移显著增加主要是因为巷道开挖引起的，与理论计算和数值模拟结果(b=0，kφ=1，kc=1/2)比较接近，进一步验证了相关理论的正确性。

因此，在巷道围岩支护设计中应适当的考虑中间主应力系数b、内摩擦角软化系数kφ和黏聚力软化系数kc对围岩的位移变化的影响。工程中常采用注浆加固和锚喷支护提高峰后内摩擦角和黏聚力，可大大的降低塑性范围、顶底板和两帮位移移近量，达到最佳的支护效果，提高巷道围岩的稳定性。

5　结论

1) 本文基于统一强度理论，考虑峰后软化和中间主应力系数b等综合影响，通过引入峰后软化系数kφ和kc，深入研究了深埋圆形巷道塑性区范围、位移和巷道周边围岩应力。

2) 随中间主应力系数b的增大，塑性区半径Rp逐渐减小，位移u逐渐降低，塑性区切向应力和围岩径向应力逐渐增大，弹性区切向应力逐渐减小，径向应力逐渐递减。因此考虑中间主应力能够提高围岩的极限强度，充分发挥围岩自身的承载潜能，降低塑性范围和变形。在实际工程实践中，要充分考虑中间主应力的作用，以使结果更加准确。

3) 峰后内摩擦角软化系数kφ和黏聚力软化系数kc对巷道围岩塑性范围和变形具有显著影响。随内摩擦角软化系数和黏聚力软化系数的增大，围岩塑性区半径和位移呈现先急剧后缓慢的减小趋势。工程中可采用注浆加固和锚喷支护提高峰后软化系数，达到降低塑性范围和位移移近量的目的，提高巷道围岩的稳定性。

4) 通过数值模拟和现场实测分析验证了有关理论的正确性，研究成果可为巷道围岩稳定性分析提供一定理论依据，以便提出合理和最优的支护设计方案。

[1]温森，杨圣奇．基于Hoek-Brown准则的隧洞围岩变形研究[J]．岩土力学，2011，32(1)：63-69．

WEN Sen, YANG Shengqi. Study of deformations of surrounding rock of tunnel based on Hoek-Brown criterion[J]. Rock and Soil Mechanics, 2011, 32(1): 63-69.

[2]Sharan S. K. Exact and approximate solutions for displacements around circular openings in elastic-brittle plastic Hoek-Brown rock[J]. Int. J. Rock Mech. Min.Sci., 2005, 42 (4):542-549.

[3]孟龙，高召宁，孟祥瑞．考虑损伤的圆形巷道围岩弹塑性分析[J]．中国安全科学生产技术，2013，9(11)：11-16．

MENG Long, GAO Zhaoning, MWNG Xiangrui. Elasto-plastic analysis of circular roadway surrounding rocks under consider ation of rock damage[J]. Journal of Safety Science and Technology, 2013, 9(11): 11-16.

[4]马念杰，张益东．圆形巷道围岩变形压力新解[J]．岩石力学与工程学报，1996，15(1)：84-89．

MA Nianjie, ZHANG Yidong. A new analysis on ground pressures around openings[J]. Chinese Journal of Rock Mechanics and Engineering, 1996, 15(1):84-89.

[5]李文婷，李树忱，冯现大，等．基于莫尔-库仑准则的岩石峰后应变软化力学行为研究[J]．岩石力学与工程学报，2011，30(7)：1460-1466．

LI Wenting, LI Shuchen，FENG Xianda，et al．Study of post-peak strain softening mechanical properties of rock based on Mohr-Coulomb criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(7):1460-1466.

[6]张小波，赵光明，孟祥瑞. 考虑峰后应变软化与扩容的圆形巷道围岩弹塑性 D-P准则解[J]．采矿与安全工程学报，2013，30(6)：903-910．

ZHANG Xiaobo, ZHAO Guangming, MENG Xiangrui. Elastoplastic solution for surrounding rock of circular roadway based on D-P criterion by considering post-peak strain softening and dilatancy[J]. Journal of Mining & Safety Engineering，2013, 30(6):903-910.

[7]翟所业，贺宪国．巷道围岩塑性区的德鲁克-普拉格准则解[J]．地下空间与工程学报，2005，1(2)：223-226．

ZHAI Suoye，HE Xianguo. Solution of D-P of plastic district of surrounding rock of roadway[J]．Chinese Journal of Underground Space and Engineering, 2005, 1(2): 223-226.

[8]刘志钦，余东明．考虑中间主应力和剪胀特性的深埋圆巷弹塑性应力位移解[J]. 工程力学, 2012，29(8)，289-297．

LIU Zhiqin, YU Dongming. Elasto-plastic stress and displacement analytical solutions to deep-buried circular tunnels considering intermediate principal stress and dilatancy[J]. Engineering Mechanics, 2012, 29(8), 289-297.

[9]俞茂宏．双剪理论及其应用[M]. 北京：科学出版社，1998．

[10]陈立伟，彭建兵，范文，等．基于统一强度理论的非均匀应力场圆形巷道围岩塑性区分析[J]．煤炭学报，2007，32(1)：20-23．

CHEN Liwei, PENG Jianbing, FAN Wen, et al. Analysis of surrounding rock mass plastic zone of round tunnel under non-uniform stress field based on the unified strength theory[J].Journal of China Coal Society, 2007, 32(1): 20-23.

[11]徐栓强，俞茂宏，胡小荣. 基于双剪统一强度理论的地下圆形洞室稳定性的研究[J]．煤炭学报，2003，28(5)：522-526．

XU Shuanqiang, YU Maohong, HU Xiaorong. The stability analysis of circular tunnel based the twin shear unified strength theory[J]. Chinese Journal of Coal Society, 2003, 28(5):522-526.

[12]胡小荣, 俞茂宏.统一强度理论及其在巷道围岩弹塑性分析中的应用[J].中国有色金属学报，2002，12(5):1021-1026．

HU Xiaorong, YU Maohong. Unified strength theory and its application in elasto-plastic analysis to tunnel[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(5):1021-1026.

[13]曾开华，鞠海燕，张常光．深埋圆形隧道弹塑性位移统一解及其比较分析[J]．岩土力学，2011，32(5)：1315-1319．

ZENG Kaihua, JU Haiyan, ZHANG Changguang. Elasto-plastic unified solution for displacements around a deep circular tunnel and its comparative analysis[J]. Rock and Soil Mechanics, 2011, 32(5):1315-1319.

[14]PARK P H, KIM Y J. Analytical solution for a circular opening in an elastic-brittle-plastic rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(4): 616-622.

[15]姚国圣，李镜培，谷拴成．考虑岩体扩容和塑性软化的软岩巷道变形解析[J]．岩土力学，2009，30(2)：463-467．

YAO Guosheng, LI Jingpei, GU Shuancheng. Analytic solution to deformation of soft rock tunnel considering dilatancy and plastic softening of rock mass[J]. Rock and Soil Mechanics, 2009, 30(2):463-467.

[16]陆银龙，王连国，杨峰，等．软弱岩石峰后应变软化力学特性研究[J]．岩石力学与工程学报，2010，29(3)：640-648．

LU Yinlong, WANG Lianguo, YANG Feng, et al. Post-peak strain softening mechanical properties of weak rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3):640-648.