一道贵州省模拟题的多种解法

云南省蒙自市蒙自一中(新校区)(661100)

苏保明●

一道贵州省模拟题的多种解法

云南省蒙自市蒙自一中(新校区)(661100)

苏保明●

随着新课改的进一步实施与推进，选修内容越来越被命题者所亲睐.选修4-5《不等式选讲》是选考内容的重要内容，其中证明不等式问题又是高考考查的重点题型之一 .本文例举一例研究不等式的证明方法，供参考.

(Ⅰ)求m的值；

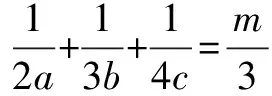
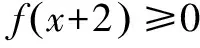
针对第(Ⅱ)问，经过笔者认真思考和研究，给出下面六种解法：

方法一、常数代入法

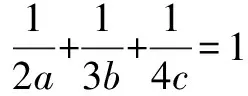
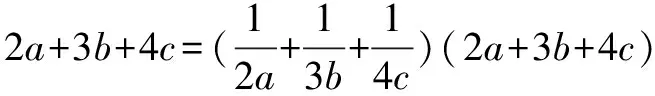
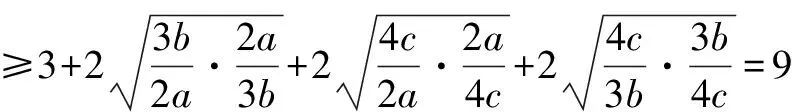
所以2a+3b+4c≥9.

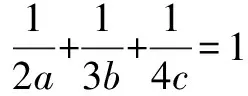
因为a>0,b>0,c>0，

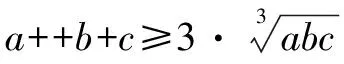
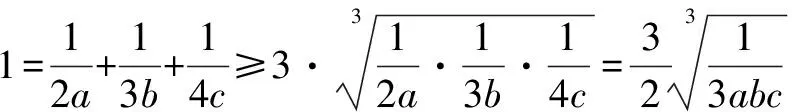
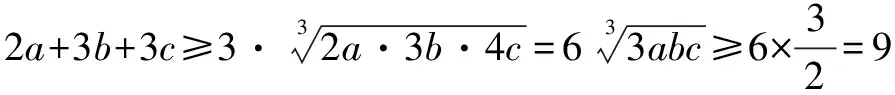
所以2a+3b+4c≥9.

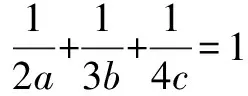
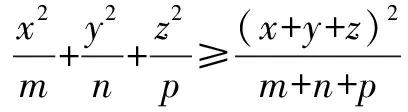
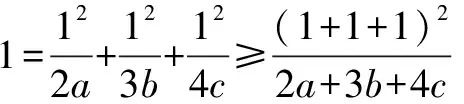
因为2a+3b+4c>0，所以2a+3b+4c≥9.

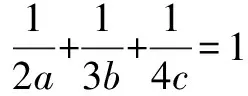
方法四：向量法

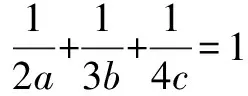
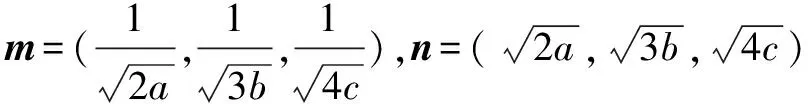
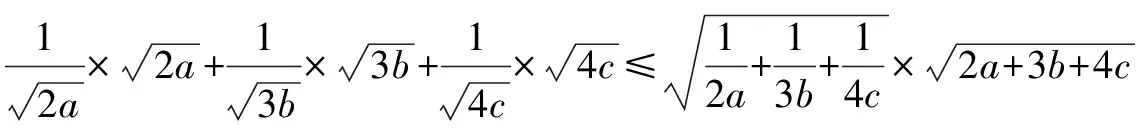
所以2a+3b+4c≥9.

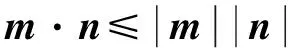
方法五、柯西不等式法

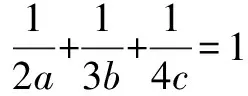
因为a>0,b>0,c>0，所以由柯西不等式，得

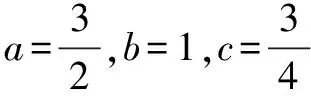
所以2a+3b+4c≥9.

评注 柯西不等式的引入，为解决某些相关的数学问题添增了新的思想方法，给解题者一种快乐感和成功感.此法通俗易懂，容易掌握，值得借鉴和学习.

方法六、利用方差的性质

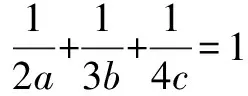
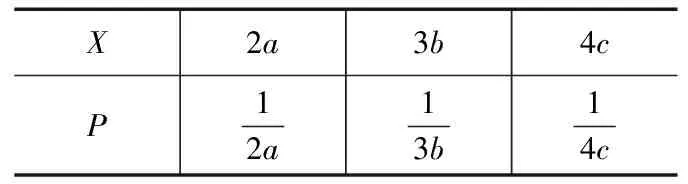
因为a>0,b>0,c>0，所以构造离散型随机变量X的分布列：

X2a3b4cP12a13b14c

所以由方差的性质EX2≥(EX)2得2a+3b+4c≥9.

评注 用此法解决问题的关键就是能正确构造离散型随机变量的分布列，而是否正确构造的关键又在于EX2≥(EX)2中是否出现所需要的式子2a+3b+4c.此法带有很强的技巧性，必须熟练掌握才能运用自如.

G632

B

1008-0333(2017)07-0005-02