极限思维法在初中物理解题中的妙用
江苏省扬州市梅岭中学(225002)
陆文彬●
极限思维法在初中物理解题中的妙用
江苏省扬州市梅岭中学(225002)
陆文彬●
在初中物理中考中,会有一些把关题,用于选拔更优层次的学生.而这些题型都会涉及到一些解题方法,本文就其中一种方法“极限思维法”,通过几个具体实例,通过对比研究常规的解题方法和极限思维法,旨在拓宽学生在中考压轴题的解题思路.比较从而体现其优越性.
初中物理;极限思维法;方法
在物理解题的过程中,有一类题用“极限思维法”去解显得特别简单.所谓“极限法”,本质上是由数学归纳演绎推理而来的一种定性的分析方法,原理是假设某种极限的物理现象或过程存在,依据题目所给的具体条件,对其进行“放大”或“缩小”以至推及“极限”,进行科学分析,从而得出正确判断或导出一般结论的方法.此方法简洁易操作,可避免复杂的数学定量计算.本文通过几个具体中考的实例,将常规的解题方法和极限法进行比较,从而体现其优越性.
一、密度压强浮力类型题
1.质量和外表都相同的空心铜球、铁球和铝球,其空心部分体积最大的是( )(ρ铜>ρ铁>ρ铝).
A.铜球 B.铁球 C.铝球 D.一样大

故答案选A.
极限法 铁球的密度在介于铜和铝之间,因此空心部分体积最大的肯定是在铜球或铝球二者选其一.可以想象铜球的密度非常之大,只需要很小体积的铜就可以了,自然空心部分就是铜最大了.故答案应选C.
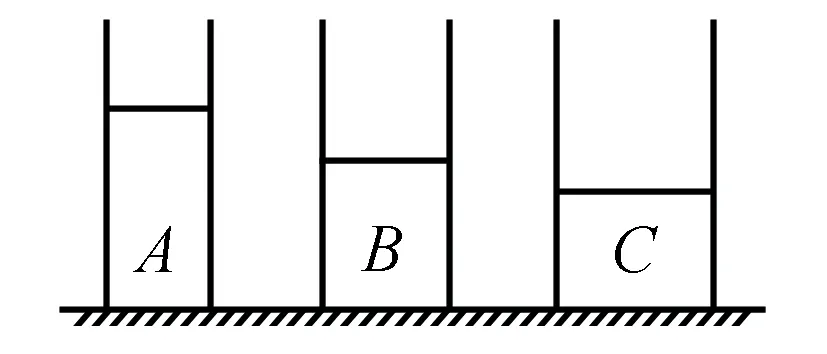
图1
2.【上海】如图1所示,三个底面积不同的圆柱形容器内分别盛有A、B、C三种液体,它们对容器底部的压强相等,现分别从三个容器内抽出相同深度的液体后,剩余液体对容器底部的压强pA、pB、pC的大小关系是( ).
A.pA>pB>pCB.pA=pB=pC
C.pA
常规解法 因为开始时三种液体对容器底部的压强相等,且容器中液体的深度hA>hB>hC,所以结合液体的压强公式p=ρgh可得,ρA<ρB<ρC.现分别从三个容器内抽出相同深度的液体,则抽取部分所产生的压强就等于容器底部减小的压强,因为抽去的液体深度相同,则容器A减小的压强最小,B次之,C减小的压强最大,所以最终A容器底部受到的压强最大,B次之,C最小,即有pA>pB>pC,答案选A.
极限法 假设抽取液体的高度与C容器中液体的高度相同,即C容器中的液体被抽完了,则该容器受到液体的压强减小为零,而另外两个容器底部还受到液体的压强,所以所受液体压强最小的是C,同理可以得出正确答案为A.

图2
3.【常州】随着全球气候变暖,漂浮于海面的冰山正逐渐熔化.小明为了探究冰山熔化后海平面是否变化,就将一块冰放入浓盐水中,冰处于漂浮状态,液面位置如图2所示.冰熔化后,杯中的液面将比熔化前( ).
A.不变 B.上升 C.下降
D.无法判断
常规解法 冰在盐水面上熔化的全过程,可看成是这样的一个过程:冰漂浮在盐水液面上相当于在盐水的上部压出了一个“坑儿”,这个“坑儿”的容积其实就等于冰漂浮时的V排;将冰拿走,“坑儿”保留在盐水面上,再将整块冰熔化成水后,倒入“坑儿”中,如果有多余则水面上升,相等则液面不变,小于则液面下降.
可以用物理量来明确表示,冰块熔化成水的体积V化水与“坑儿”的容积相比较,其实就是V化水与V排相比较:(合理的假设能帮助我们解题)
若V化水>V排,则液面上升;V化水=V排,则液面高度不变;V化水 因此,只要比较出V化水与V排的关系,便可分析出水面的变化情况. 极限法 如果冰块是漂浮在水中,那么冰块化成的水恰好填补冰压在水里的坑,液面是不会升降的.题中冰块是漂浮在盐水中的,极限法可以想象冰块是漂浮在密度极大的液体中比如水银中,那么冰块压在水银里的坑很小,冰块熔化后的水填满小坑并将多出来的水铺在水银上面.故答案应选B. 1.如图3所示,杠杆上分别放着质量不相等的两个球,杠杆在水平位置平衡,如果两球以相同速度同时匀速向支点移动,则杠杆( ). 图3 A.仍能平衡 B.不能平衡,大球那端下沉 C.不能平衡,小球那端下沉 D.无法判断 常规解法 设左右两个球的质量分别为M、m,▶由题意可知,M>m.根据杠杆的平衡条件F1l1=F2l2可得:Mgl左=mgl右,当两球以相同速度同时匀速向支点移动l后,左侧力与力臂的乘积为Mgl左-MgL;右侧力与力臂的乘积为mgl右-mgL.因为M>m,可推知移动后左侧力与力臂的乘积小于右侧.因此,杠杆不能平衡,小球端下沉,故答案应选C. 极限法 由于左边球距O点较右边球距O点近,而两者速度相等,大球将先达到O点.当大球到O点时,小球还没到,则杠杆一定会向小球那端倾斜.故答案应选C. 图4 2.如图4所示,作用在杠杆一端且始终与杠杆垂直的力F,将杠杆缓慢地由位置A拉至位置B,在这个过程中动力F( ). A.变大 B.变小 C.不变 D.先变大后变小 常规解法 由图可知,O是支点.根据杠杆的平衡条件F1l1=F2l2,阻力臂一直增加,阻力与阻力臂的乘积也一直增加.若要保持平衡,在动力臂不变的情况下,只有增加动力.故答案应选A. 极限法 假设杠杆在吊着物体在竖直位置的最低端,此时无需任何拉力就能平衡,当拉到图B位置时,F必然要大于零.故答案应选A. 综合以上各例题的对比分析,可以看出有的试题用常规方法按部就班的去解题既耗时又麻烦.要敢于打破常规,化繁为简,一旦应用得恰当,就能出奇制胜,在应试中时间大大缩短.需要说明的是并非任何问题都可用极限法求解,换句话说其使用也是有条件的,对非单调变化的函数应慎用极限法.比如滑动变阻器与某一电阻串联,滑片P应如何调节才能使滑动变阻器的功率达到最大.因此合理应用“极限法”解题的关键在于:要能够透过题目抓住促成问题变化的内在原因,并用发展变化的眼光对此内因进行深刻剖析,创造性地发现问题背后隐含的“极限”,最终迅速、便捷地解题. 课题名称:初中物理高效课堂教学模式的建设与研究;课题编号:2013JK10——Z049. G632 B 1008-0333(2017)08-0065-02
二、杠杆平衡类