高等数学与初等数学衔接问题的探究——以对数函数为例

北京工业大学实验学院(101101)

甘 艳●

高等数学与初等数学衔接问题的探究
——以对数函数为例

北京工业大学实验学院(101101)

甘 艳●

自19世纪以来，数学的呈现方式日趋形式化.定义、定理、证明、推论等均以简洁而抽象的方式陈述.《高等数学》呈现的数学过程，是一种严密的学术形态，呈现出来的是冰冷的美丽.大学新生在知识准备、学习方法、学习心理、自学能力等方面容易出现问题.本文将以对数函数为例，以建构主义学习理论和认知结构说为指导依据，探究关于对数函数的定义、运算性质、求导等方面的衔接问题，建立高等数学与初等数学的联系，使学生尽快顺利地适应从中学到大学的学习.

初等数学；高等数学；衔接

2002年至今，北京市中学数学教学经历了多次改革.部分内容进行了删减，如对数公式、三角函数公式、反三角函数、极坐标等；增加了部分内容，如极限、导数、定积分等内容.中学数学教学内容、教学方式和教学方法的改革必将直接影响高等数学的教学.在近五年的教学中，笔者发现部分学生高中已学内容仍然存在过渡的困难.为了解决这部分的问题，笔者将以对数函数为例，探究高等数学与初等数学衔接存在的问题，并提出解决方案.

一、建构主义的学习理论

建构主义学习理论的基本思想是，学习是学习者主动建构内部心理结构的过程.美国心理学家维特罗克提出了学生学习的生成过程模式，他认为学习的生成过程是学生已有的知识经验(即原有认知结构)与从环境中主动选择和注意的信息相互作用、主动建构信息的意义的过程.这一模式说明，学习总是要涉及学生原有的知识经验，并利用这些经验来理解和建构新的知识.

二、学习迁移的理论——奥苏伯尔的认知结构说

奥苏伯尔提出一切有意义的学习都是在原有学习的基础上产生的，而过去经验对当前学习的影响不是直接发生的，而是通过认知结构的特征发生影响的，这些特征是指学生在一定知识领域内的认知的组织特性，如清晰性、稳定性、概括性和包容性等.如果学生在某一领域的认知结构清晰度、稳定性、概括性和包容性高，迁移发生的可能性就大.

上面两种关于学习的理论都提到了学生的已有知识结构，提出了影响新旧知识建构和迁移的诸多因素，教师在教学过程中要注意学生的原有认知结构，学生对所学内容的认知的清晰性、稳定性、概括性和包容性.

三、学生目前的学习状况

部分数学优秀的学生可以轻松地跨过“抽象”的门槛，严密地按形式化的叙述把握数学知识.但是，多数学生不能很自然地接受数学，把数学思想和方法看成“天书”，无法和自己的思维挂钩.下面将以对数函数为例，将新旧知识进行罗列，给出教师教学和学生学习的建议.

四、高等数学教学中出现的对数问题

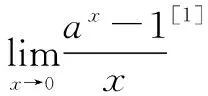
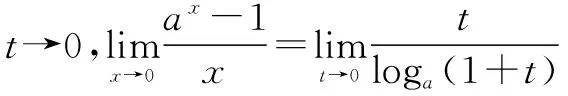
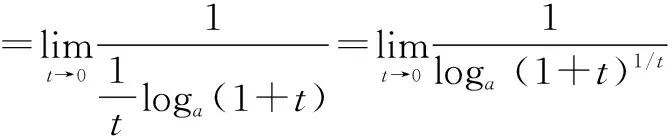
学生的原有认知结构：

(1)对数的定义；

(2)对数的运算性质；

(3)对数的换底公式；

(4)第二个重要极限公式.

学生要学习的新知识：

(1)极限的计算；

(2)等价无穷小.

教学建议：

(1)知识准备:教师提前复习对数的定义、运算性质、换底公式；

(2)方法要总结：前面的计算部分是围绕指数函数、对数函数的转换及第二个重要极限的应用，所以这里是先变换再计算极限(这种方法经常用在不能直接求函数的极限问题上，有普遍性)；

(3)学生要主动在已有的知识经验的基础上与从题目的已知部分选择对数部分的变换和极限计算的过程，这是能否解出该题的关键.

二、求y=logax的导数.

分析 可以用导数定义，也可以用反函数的导数公式.这里，笔者建议两种方法都用，进行比较.

方法二 按反函数的求导方法，

设x=ay(a>0,a≠1)为直接函数，则y=logax是它的反函数，已知函数x=ay(a>0,a≠1)在区间Iy=(-∞,+∞)内单调、可导，且(ay)′=aylna≠0.

解x=ay(a>0,a≠1)在区间▶Iy=(-∞,+∞)内单调、可导，

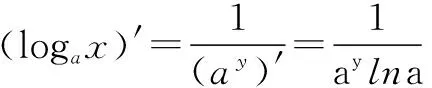
学生的原有认知结构：(1)对数的定义；(2)指数函数的导数公式；(3)反函数的导数公式；(4)第二个重要极限公式.

学生要学习的新知识：对数函数的导数公式.

三、求y=xsinx(x>0)的导数

分析 这个函数是幂指函数，为了分离底数和指数，我们最先考虑的是对数公式，这里有两个方法：

方法一 y=xsinx(x>0)，两边同时取对数，

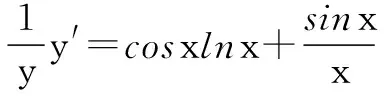
学生的原有认知结构：(1)对数的定义；(2)导数的乘法法则；(3)复合函数的求导法则.学生要学习的新知识：对数函数的导数公式.

教学建议：(1)引导学生思考分离底数和指数的方法，写出对数公式；(2)教师要指出这里lny是y的函数，而y是x的函数.所以，对于lny的求导，应该用复合函数求导法则；(3)幂指函数形式的计算问题可以考虑用取对数的方法.

教学是一个复合词，包括教和学两个方面，是由教师的教和学生的学所组成的双边活动过程.教学是一个非常复杂的过程，教师要引导学生积极思考、学会提问，学会总结，引导学生积极参与到教学活动中来.通过高等数学的教学，教师要教给学生数学知识，提高学生数学素养，培养学生自主学习和应用数学解决问题的能力.

[1]同济大学数学系.高等数学[M].北京：高等教育出版社，2014.

师的指导下，重复专业研究人员的科学探究过程.这个活动又叫做获得间接经验，但这间接经验的获得，却因为大脑镜像神经元的“模仿”，形同“亲历”.

二、“直观”教学情景创设的原则：直观

依据“镜像神经元”的功能及相关教育教学理论，在化学教学中创设“直观”情境，重视学生的视觉的思维能力，把知识教学中遇到的重点、难点、疑点，尽可能转化为符号、图形、图表等直观方来呈现，再合适不过.本文所指“直观”教学情境创设是基于“镜像神经元理论”启示下的“直观”教学情境创设.(以下简称“直观”教学情境创设).

笔者认为在进行相关教学设计和实际教学应用中，“直观”是最重要的关键词.因此直观性原则应该是“直观”教学情景创设的总原则.直观原则包括两个方面，一是教师方面，教学过程的直观、可视化，教学语言的直接，教学测试的可视化.二是学生方面，学习过程注意其“眼睛”的学习能力的发挥和发展，协调视觉对其感性与理性的共同影响.

三、“直观”情景创设应用之“物质的量”教学设计

“物质的量”是高中化学的核心概念之一，也是具有功能价值的工具性的概念.

1.教学策略选择

教学策略分为三点，即：创设“直观”教学情境凸显学习意义(为何学)→运用一定思维方法(如何学)→运用新知识解决问题(如何用)

(1)为何学：创设用微观粒子数描述宏观物质很困难的情境；

(2)如何学：利用联想、类比、归纳的方法学习物质的量、阿伏加德罗常数和摩尔质量.

(3)如何用：在如何用中，利用所学新知识思考他们之间的关系.

2.教学流程

环节一：为何学

举一个例子：1滴水，10亿人来数其中的水分子，每人每分钟数100个，日夜不停，需要3万多年才能数完.来说明如果我们用微观的粒子数来描述宏观物质很不方便.那我们怎么办呢？

教师提出在生活中我们也遇到过类似的问题，但是问题都不攻自破，比如，这么多啤酒，你一下子想到的一定是一箱啤酒，类似，一打铅笔、一双鞋子等，他们都是把微小物质扩大倍数形成一定数目的集体，以方便研究.物质是由大量的分子、原子或离子构成的.类比到微观世界，我们也可以用这种打包的思想，把粒子打包成一堆儿，用多少堆儿来描述宏观物质.这样就顺理成章的提出物质的量的概念.

环节二：如何学

利用联想、类比、归纳的学习方法学习物质的量、阿伏加德罗常数和摩尔质量这三个概念.

任务一：提出物质的量的定义

物质的量表示的是一定数目粒子的集合体，物质的量的定义过于抽象，当定义不容易理解的时候，这种外延性的解释就显得尤为重要.

任务二：提出物质的量的单位——摩尔

物质的量是七大国际物理量之一.(简单介绍摩尔其人.)

任务三：解释阿伏加德罗常数

教师提出：箱是24个，打是12个，那么1 mol有多少个呢？国际规定：1mol任何粒子所含的粒子数与0.012 kg12C中所含的碳原子数相同，约为6.02×1023.把1mol任何粒子的粒子数叫做阿伏加德罗常数，符号为NA.

任务四：提出摩尔质量的概念

教师引导：0.012 kg12C跟初中学习的相对原子质量的概念很类似，引出相对原子质量的回顾.

教师再次提出为什么国际规定一摩尔任何粒子的粒子数约为6.02×1023呢？既然是人为规定，为什么会规定这么一个不容易记的常数，而不规定一个容易记的常数呢？

给出一个表格，进行1mol物质的计算，发现，只有这么规定，1mol粒子的质量在数值上恰好等于其相对原子质量或者相对分子质量.而规定别的容易的任何数字为1mol粒子的数量时，成百上千的宏观物质的摩尔质量很不好记.表格最下面是一摩尔物质的质量，也是用微观描述宏观的另一个角度，从而引出摩尔质量的学习.

摩尔质量：单位物质的量的物质所具有的的质量叫做摩尔质量，用M来表示.1mol任何粒子的质量以克为单位时，其数值与该粒子的相对原子质量或者相对分子质量相等.教师再次说明这并非一种巧合，在规定NA的时候就注定有这样的结果.

环节三，如何用

我们利用m(物质)=粒子数×每一个粒子的质量来计算，粒子数太大，每一个粒子的质量太小，不利于计算.通过一个表格呈现，刚刚学习了的粒子数和物质的量之间的关系，可以把粒子数转化成物质的量，然后为了让等式两边相等，还必须得把每一个粒子的质量乘以NA，这样总结出物质的量和宏观质量的关系.

3.教学设计分析

本节课注重学生思维能力的方法，面对特别抽象的概念的时候，运用直观的教学形式呈现，减轻学生思维压力，同时，“看透”概念本质.也体现了“直观”教学情境创设的“直观”性原则.主要解决物质的量，阿伏加德罗常数，摩尔质量三个抽象概念的抽象关系.并在宏观的物质和微观的粒子之间建立起化学计量的桥梁.

课堂教学中，教师创设特定的“直观”情境，首先吸引住学生的注意力，再根据情境的意义，引发学生的兴趣.学生只要“看到”就会有思考，这是有效教学的前提.总的来说，“镜像神经元理论”告诉我们，人的视觉是有思考能力的，有着高级的智慧，所以一个合适的“直观”情境会引发学生顿悟的思考，甚至可以让学生一眼就看到知识的本质.

参考文献

[1-4]陈建翔.“镜像教育”:一个教育新主题的开始——论镜像神经元的教育内涵及对教育变革与创新的启发[J]. 教育科学. 2011(05)

[5]Giacomo Rizzolatti&Laila Craighero.The Mirror NeuronSystem [J].Annual Review of Neuroscience，2004 (27) ．

[6]鲁道夫·阿恩海姆.视觉思维[M].光明日报出版社.1987.

▶

G632

B

1008-0333(2017)09-0023-02