基于粗糙集RBF神经网络村镇山洪灾害损失预测研究——以神农架林区为例

李祎琛，何亚伯，汪 洋

(武汉大学 土木建筑工程学院，湖北 武汉430072)

基于粗糙集RBF神经网络村镇山洪灾害损失预测研究
——以神农架林区为例

李祎琛，何亚伯，汪 洋

(武汉大学 土木建筑工程学院，湖北 武汉430072)

以神农架林区为研究对象，从致灾因子、孕灾环境、承灾体因素以及区域应灾能力四个角度选取山洪灾害损失预测因子，并利用粗糙集对预测因子进行约简，以实现对预测模型输入指标的优化，针对山洪灾害损失作用机理的复杂性、不确定性，选择RBF神经网络模型对灾害损失进行预测。结果显示粗糙集理论方法可以有效地判别提取与山洪灾害密切相关的预测因子，显著地提高了模型对灾害损失的预测精度；基于粗糙集RBF神经网络模型对山洪灾害损失的拟合效果较好，预测精度高，相对误差普遍保持在3%左右，改进后的模型具有较高的实用价值。

山洪灾害；损失预测；粗糙集；RBF神经网络

自然环境的日益恶化和人类生产活动对地质地貌的开发性破坏，使得我国中西部山区丘陵地带山洪灾害日益频发[1-3]。而受制于落后的经济、教育、医疗以及防灾减灾工程设施，山区村镇的承灾和救灾能力有限，山洪灾害发生的易损性更为突出，“因灾致贫、因灾返贫”现象时有发生，山区村镇山洪灾害现已成为阻碍社会经济可持续发展的重要障碍[3-4]。在过去的5年里，因突发性、局部性极端强降雨引发的山洪灾害造成的死亡人数比例呈递增趋势，直接经济损失更是无法估计[5-6]。

一直以来，洪水灾害是国内外专家学者研究的热点问题，如洪水风险评估、风险预警、灾害易损性评价以及综合考虑经济、社会、人口、环境的洪水灾害风险评价方法和指标体系研究等[7-13]。在灾害损失预测方面，研究发现洪水灾害损失、区域地理位置与防灾能力之间存在密切联系，当洪灾发生在村镇山区等防灾能力较弱的区域时，尽管灾害风险水平较低，但灾害的易损性更为严重[14]。而当前，我国村镇山洪灾害损失预测的研究还处于初探阶段，对灾害损失预测多以时间序列模型进行趋势拟合，利用灾损度指数从有限的样本数据中模拟灾害损失与时间的耦合关系，依赖于精确统计的灾害横断面数据。其中，常用的方法主要有回归方程、支持向量机、数据包络分析等[15-21]。虽然上述方法在一定程度上对山洪灾害损失进行了合理的预测，但山洪灾害的发生具有较大突发性，是气象灾害和地质灾害并发的结果，特定的承灾体和孕灾环境对山洪灾害损失程度具有较大影响，并且考虑到山洪灾害损失有效的横断面数据较少、致灾机理复杂不明，以时间序列为基础的拟合模型预测精度较差，研究方法也并未考虑到各因素对于灾害损失综合影响程度。因此本文以神农架林区山洪灾害损失预测为例，从致灾因子、孕灾环境、承灾体因素以及区域应灾能力等角度选取预测因子，采用粗糙集对预测因子进行约简，实现对预测模型输入指标的优化，并针对山洪灾害与损失之间作用机理的复杂性、山洪灾害有效统计数据不足，利用RBF神经网络模型在解决不确定性问题方面的优势，对灾害损失进行预测，根据预测结果可以为村镇规划综合风险评价和政府灾时快速决策提供前瞻性的依据。

1 数据来源与研究路线

1.1 研究区域与数据来源

神农架林区位于湖北省西部，处于第二阶梯第三阶梯的交界处，由大巴山脉东延的余脉组成中高山地貌，区内山体高大，由西南向东北逐渐降低，是中纬度自然环境过渡的交错区域，平均海拔1 700 m。神农架林区地处中纬度北亚热带季风区，受大气环流控制，气温偏凉且多雨，年降水量900～1 000 mm。特定的地质背景、地理位置和气候条件使得神农架林区成为山洪灾害频发地段，不利于社会经济的可持续发展，不利于生态资源的开发与保护。其中，研究区域位置如图1所示。

文中山洪灾害的资料主要参考自《神农架地区统计年鉴》和《山洪报告》以及实地调研。以1983-2013年之间在神农架地区发生并造成一定经济社会损失的18次山洪灾害为样本进行灾害损失预测，并对数据资料采用统一统计标准，以保证数据资料能真实反应灾害情况，确保预测的可信度。

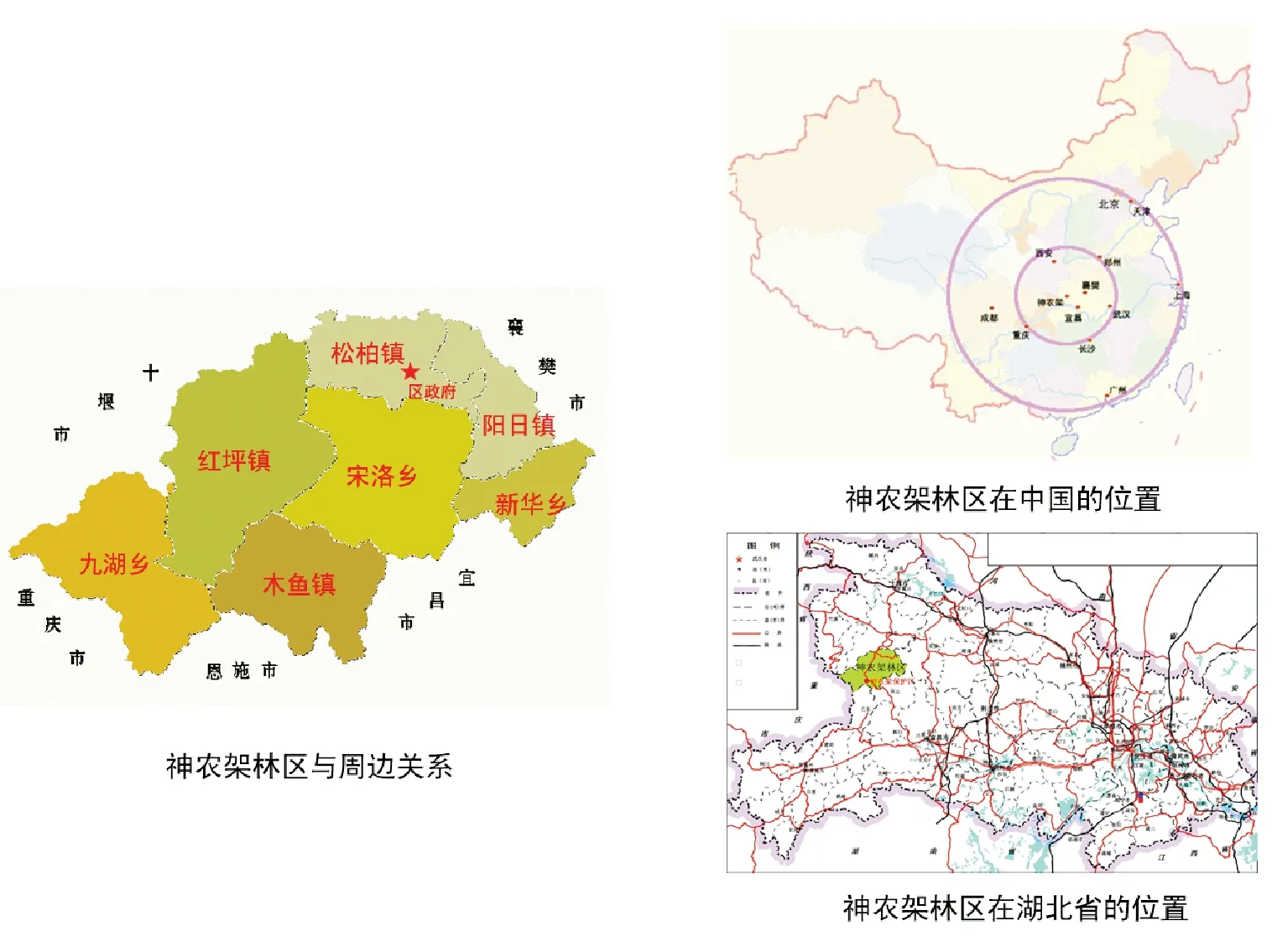
图1 神农架林区地理位置图

1.2 研究技术路线

灾害损失预测是防灾减灾工程的重要一环，与灾后损失评估相比，灾前或灾时的损失预测能够提前获得灾害等级信息，将极大提高救灾时效性，有助于政府快速决策，合理调配救灾物资和人员，减少灾害损失及影响，对防灾减灾工作和村镇社会经济发展具有重大意义。

本文首先应用粗糙集理论对影响灾害损失的因素进行约简分析，去除冗余属性，得到影响灾害损失的决定性因素；然后以约简后的因素作为输入指标，利用RBF神经网络进行灾害损失预测。研究的技术路线如图2所示。

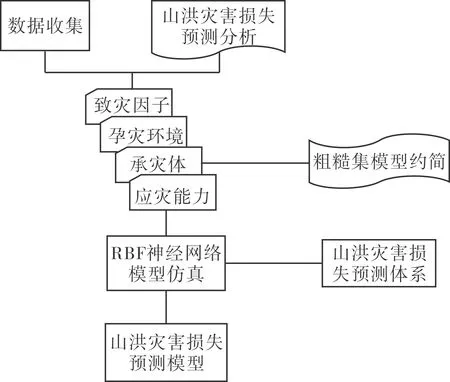
图2 村镇山洪灾害损失预测流程图

2 预测指标体系构建

2.1 预测指标体系初判

预测因子是科学预测灾害损失的基础，因子的选择不仅要遵从科学性、可行性和综合性等基本原则，还要符合山洪灾害的基本规律和研究区域的地理特征[22-23]。本文从山洪灾害致灾机理的角度对诱发灾情的指标因子进行选择，分析如下：

山洪灾害是气象灾害和地质灾害的并发，而灾情是致灾因子、孕灾环境、承灾体因素以及区域应灾能力共同作用的结果[24]。降雨是诱发山洪灾害的直接致灾因子，降雨量和降雨历时与山洪灾害的形成发展密切相关[25]。通常，降雨量的大小对激发泥石流起着重要作用，而降雨历时长短则决定了滑坡的发生。

孕灾环境一般考虑地形坡度、高程和植被覆盖率等因素的共同影响。地形地貌是影响村镇山洪灾害形成和发展的下垫面因素[26]。神农架地区地形坡度陡峭、相对高差大，相同的降雨量下不仅易集中地表径流，同时较大高差所累积的势能也会加大流水对地表的冲刷，而植被覆盖则减弱了山洪灾害的致灾因子和次生灾害，增强了土壤的应力和稳定性，降低了山洪灾害发生的风险概率。因此本文中选择地形坡度、关联灾害(滑坡体积)和植被覆盖率等孕灾环境因子作为模型的输入变量。

承灾体是指受到灾害影响和损害的人类社会主体，包括人类本身和社会经济发展的各个方面，如房屋建筑物、道路交通设施、农田水利等[26]。承灾体是山洪灾害直接的作用物，灾害损失程度除了与致灾因子的强度有关，很大程度上取决于承灾体的脆弱性。研究目标、对象不同，承灾体的层次也不同，就神农架林区而言，选择人口体能倍数、人口密度、耕地面积、公路里程、固定资产投资、区域人均收入、危险区固定资产价值等因子作为模型的输入变量。

区域应灾能力考验一个地区灾害险情发生时的应急水平，区域应灾能力强，对于灾害能够做到及时预警、及时抢救，可以大大降低灾害发生的损失，选择区域消防人员数、广播覆盖率、防洪堤坝长度作为模型的输入变量。

对于山洪灾情而言，最受关注的是财产损失和人员伤亡状况，其中财产损失中农作物受灾面积、受损房屋、直接经济损失是核心灾情；不同于其他自然灾害，由于爆发突然、难以预测、危险性高，山洪灾害造成的人员伤亡依旧是山洪灾情的最主要的反映。因此，本文选择人员伤亡和财产损失状况作为模型的输出变量，其中包括以下指标：受灾人数、农作物受灾面积、损伤房屋及直接经济损失。

因此参考现有自然灾害损失预测输入变量体系、山洪灾情状况以及神农架林区自然社会特征[28-30]，整理出如图1所示15个预测因子以及4个灾情定量预测输出指标。

2.2 预测指标体系约简

粗糙集是一种刻画不完整性、不确定性的数学工具，具有较好的数据知识挖掘功能，能够筛选冗余数据中隐含的关键信息，并不影响原有的分类效果及评价结果[31-32]。

2.2.1 粗糙集基本理论

影响山洪灾害损失的指标体系是一个复杂的灰色系统，冗余的指标信息输入不仅加重了预测模型的负担，而且降低模型的泛化能力[30]。本文引入粗糙集理论对复杂的指标体系进行约简，在不需要先验知识的情况下删除一些无用的因素，实现了对预测模型输入变量的优化。基于粗糙集理论预测指标的优化约简及其权重的确定分为以下几个步骤。

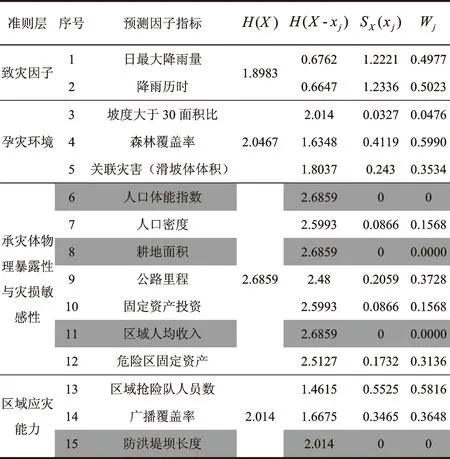
表1 山洪灾害损失预测指标体系

(1) 构建预测模型输入指标信息表

S=(U,X,V,f)。

(1)

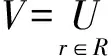
(2)计算决策表中条件属性等价类关系集合ind(B)(B⊆X)

等价关系ind(B)构成了U的一个划分，用U/ind(B)={A1,A2,…,An}表示，其中Ai用来表示不同的等价类，在ind(B)下与X不可分的所有对象构成一个等价类可记为[A]ind(B)。

(3)根据(2)中求出的等价类关系集合，计算其重要程度

在信息系统S=(U,X,V,f)中，a∈A的重要性定义为：

SX(x)=|H(X)-H(X-x)|。

(2)

式中：H(X)表示所有属性组成的集合X的信息熵；H(X-x)表示集合X除去属性x的信息熵。SX(x)越大表明该属性的重要程度越高。

定义一个属性子集B∈X的信息熵H(B)为：

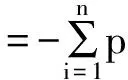
(3)

式中：U/ind(B)={A1,A2,…,An}，p(Ai)=|Ai|/|U|表示等价类Ai在U中的概率，|U|表示集合U的“势”，|Ai|表示集合Xi的“势”。“势”可用集合元素的个数表示。

(4) 计算每个评价指标的权重Wi

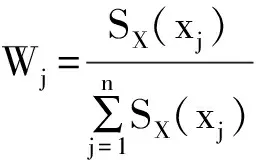
(4)

根据权重的大小来决约简的指标，权重越大，表示该指标对整个系统的影响越大，约简后信息损失越多。当指标权重为0时，该指标对整个系统几乎没有影响，应该被约简掉[33]。

2.2.2 连续属性离散化

粗糙集理论是在分类机制的基础上，利用已知的知识库将不精确或不确定的知识进行近似刻画，它的处理对象是离散化的值或属性[31-32]。因此，连续属性的离散化是粗糙集计算的基础，其根本目的是在保证预测系统信息有效性的前提下，对预测系统进行优化约简，将属性空间或值域空间划分为尽可能少的子空间，以消除指标因素之间的共线性，提高预测指标的有效性、简便性。

本文选取等距离散化的方法，将每组属性值进行等距离划分，其具体步骤如下：

(1)划分每组属性值的取值范围，确定最大值xmax和最小值xmin；

(2)设定划分区间的数目n，此处取n=3；

(3)计算区间步长d=(xmax-xmin)/n；

(4)计算区间划分点的值，即c0=xmin，c1=c0+xmin，…，cn=xmax。

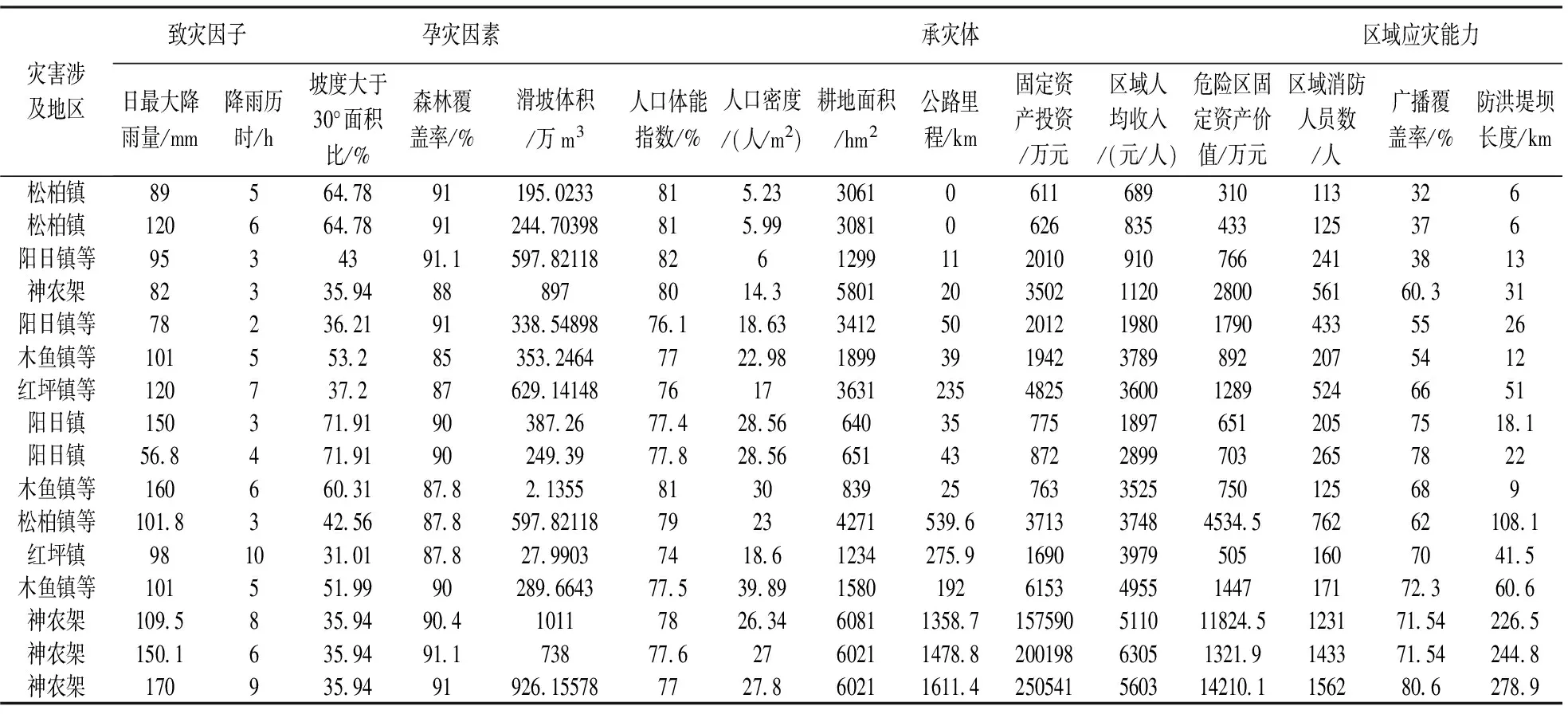
表2 原始数据表

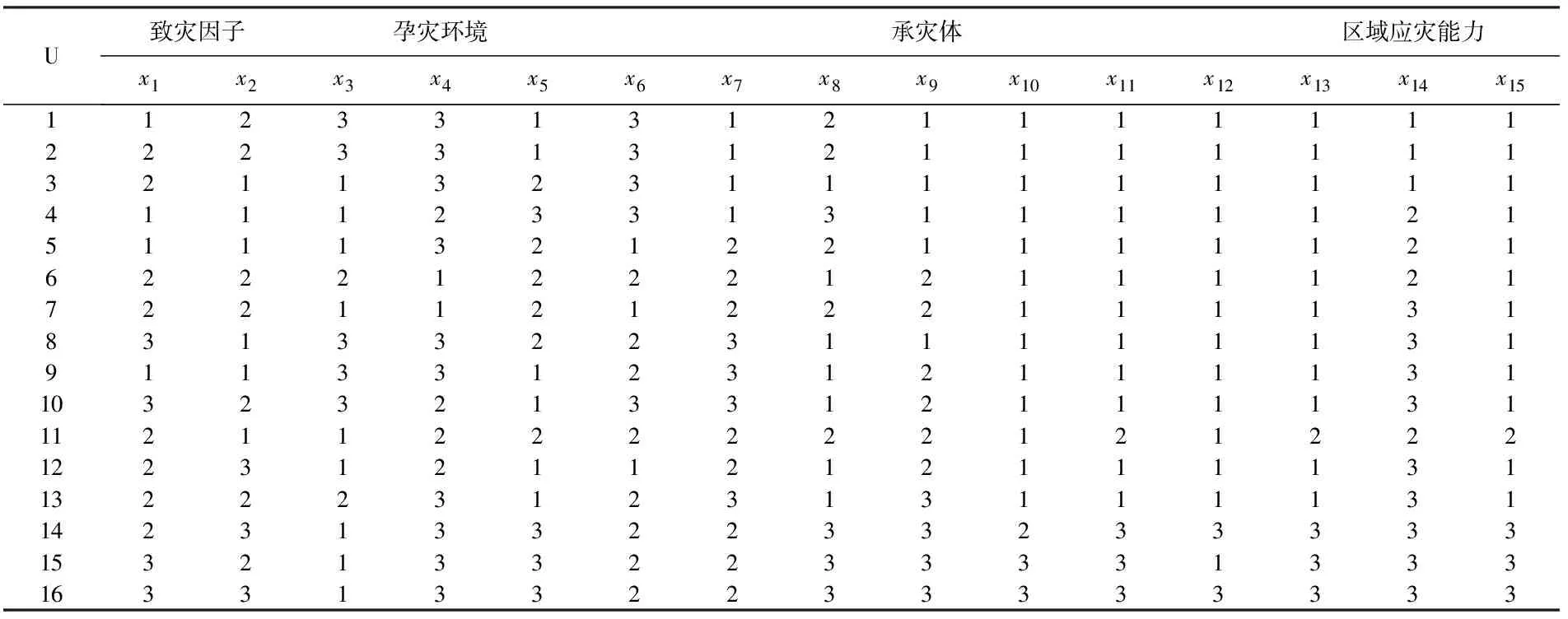
表3 预测因子离散化信息表

判断每组属性值x位于哪个区间，确定离散化后的信息表属性值p，当时ck-1≤x≤ck，p=k,k=1,2,…，n,特殊地，当x=cn时，p=n。

原始数据表见表2，对原始数据进行n=3的等距离离散化后得到信息表如表3所示。

2.2.3 预测因子优化结果

(1)构建致灾因子信息系统S=(U,X1,V,f)，其中，属性X1={x1,x2}；U={a1,a2,…,a16}。

(2)对于致灾因子所对应的属性集X1={x1,x2}，运用Matlab7.0计算变成可成：

(5)

(3)计算致灾因子指标的重要程度

(6)

(4)计算各指标的权重

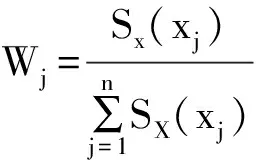
在粗糙集优化预测因子指标时，约简指标过多，信息量丢失严重，达不到全面决策的精度；约简指标过少，则达不到剔除无用信息的要求。当Wi为0时，此指标被约简[33]。

同理求得表2中所有预测因子的重要度SA、权重Wi，将计算结果汇总可以得到表4(灰色表示删除变量)。

根据权重为0的筛选原则对指标因子进行约简，由表4的计算结果可知：

(1) 人口体能指数、耕地面积、固定资产投资以及防洪堤坝长度等指标的权重为0，此类指标对整个预测模型的影响度较小。

(2) 根据信息量表中权重的大小分析可知，降雨历时、森林覆盖率、公路里程、区域抢险队人员数是预测山洪灾害损失的重要指标因子。其中，降雨历时属于致灾因子，对山洪灾害的爆发起着重要的诱导作用；森林覆盖率属于孕灾环境因子，森林覆盖率越低，同等降雨量下山洪灾害爆发的可能性越高；公路里程属于承灾体的状况，神农架地区地形陡峭，交通不便，公路里程的长短不仅关系到承灾体的脆弱性，更关系到灾后的救援通畅；区域抢险队人员数是区域应灾能力的直接体现，对灾后抢救起着重要的作用。

(3)根据表4的分析结果，以及权重大小的约简原则，剔除人口体能指数、耕地面积、固定资产投资以及防洪堤坝长度这四个指标，最终选择降雨历时、日最大降雨量、区域抢险队人员数、森林覆盖率、广播覆盖率、关联灾害(滑坡体体积)、公路里程、危险区固定资产、人口密度、固定资产投资等指标作为RBF神经网络预测模型的输入变量。

表4 预测因子指标信息量表

3 预测模型与结果分析

3.1 预测模型构建

由于自然环境的复杂性和瞬变性[1]，山洪灾情与预测因子之间的作用机理和影响机制难以用普通的线性回归模型进行模拟。鉴于山洪灾情与预测因子之间复杂的耦合非线性关系，本文选用RBF神经网络模型对山洪灾害损失进行模糊定量预测。

RBF神经网络是一种高效的前馈式神经网络[28-32,34]，这种神经网络模型结构简单、训练高效，具有最佳逼近性能和全局最优特性，可实现对非线性系统的建模，具有良好的泛化能力。RBF神经网络由输入层、隐含层、输出层构成。其中输入层与隐含层之间是简单的非线性映射，隐含层中的径向基函数负责对输入变量进行处理，然后线性映射到输出层。其网络结构如图3所示。

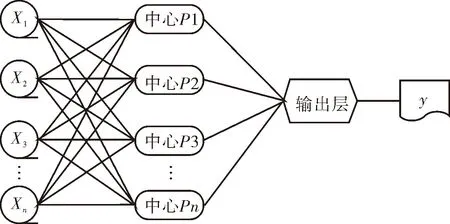
图3 RBF神经网络结构示意图

3.2 预测模型结果与分析

3.2.1 RBF神经网络模型分析

根据调研获得的神农架地区1983-2013年发生的18次山洪灾害为预测样本，随机挑选两个样本作为独立样本(编号：17、18)，以剩余的16次山洪灾害为粗糙集约简和RBF神经网络模型的训练样本，依次利用其中15样本预测剩余一个样本的损失值，如此循环计算对山洪灾害损失进行模拟预测，并计算预测值与实际值之间的相对误差率来检验模型的精度。

根据表5中预测结果的相对误差，绘制有关于模型输出变量相对误差折线图4，并对其误差走势进行相应的分析。

(1) 根据表4的预测结果可知，基于粗糙集RBF神经网络模型的预测误差相比直接利用RBF神经网络模型的预测误差要小。从神经网络模型预测的整体效果来看，在经过优化约简后，输出变量的相对误差显著改善：直接经济损失的平均相对预测误差率从11.70%降为2.68%；农作物受灾面积的平均相对预测误差率从9.23%降为3.59%；损伤房屋面积的平均相对预测误差率从7.29%降为2.26%；受灾人数的平均相对预测误差率从17.25%降为4.66%。这表明，经过粗糙集优化简约预测因子指标体系后，RBF神经网络模型的相对预测误差明显下降，预测精确度显著提高，模型预测的可靠性进一步改善。

(2) 根据图3的预测结果对比可知，基于粗糙集RBF神经网络模型对山洪灾害损失的拟合效果较好，预测精度高，普遍的相对误差保持在3%左右，预测结果误差曲线更为平缓，改进后的模型具有较高的实用价值。

由此可见基于粗糙集RBF神经网络模型能够通过优化约简原预测系统数据，有效地判别提取了与山洪灾害密切相关的预测因子，显著地提高了模型对灾害损失的预测精度。

3.2.2 独立样本测试

为了进一步检验模型预测的准确性，本文利用未参与预测模型训练的17、18号山洪灾害进行独立样本测试。分别用普通RBF神经网络模型和粗糙集RBF神经网络模型对样本进行预测，得到的预测结果如表6所示。

根据表6预测结果的对比分析可知，粗糙集RBF神经网络能明显的降低预测误差，输出结果比较稳定，模型的预测精度得到了较好的改善。

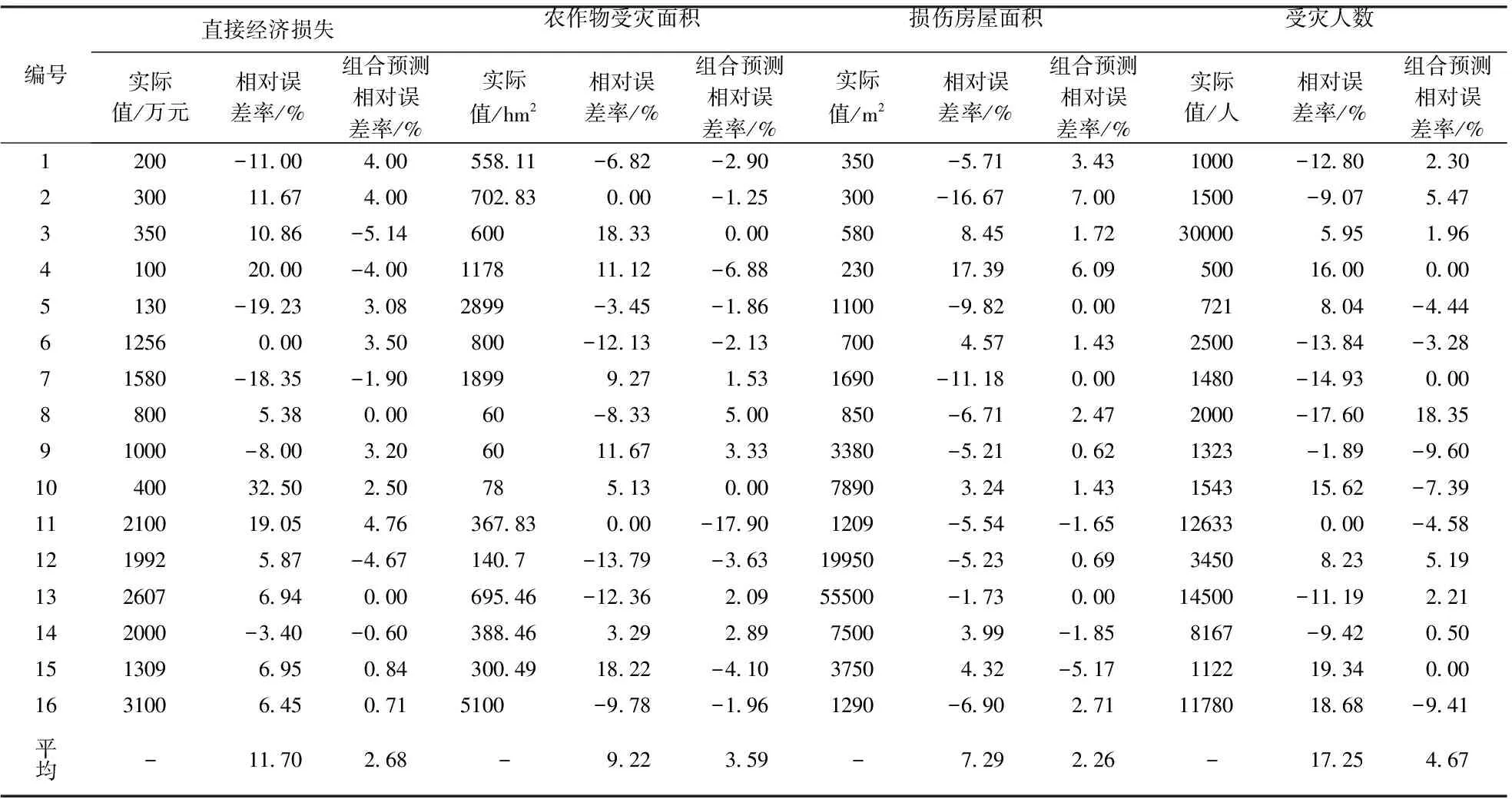
表5 基于粗糙集RBF神经网络预测结果

注：负号表示预测值小于实际值；组合预测是指经粗糙集约简后的RBF神经网络预测。

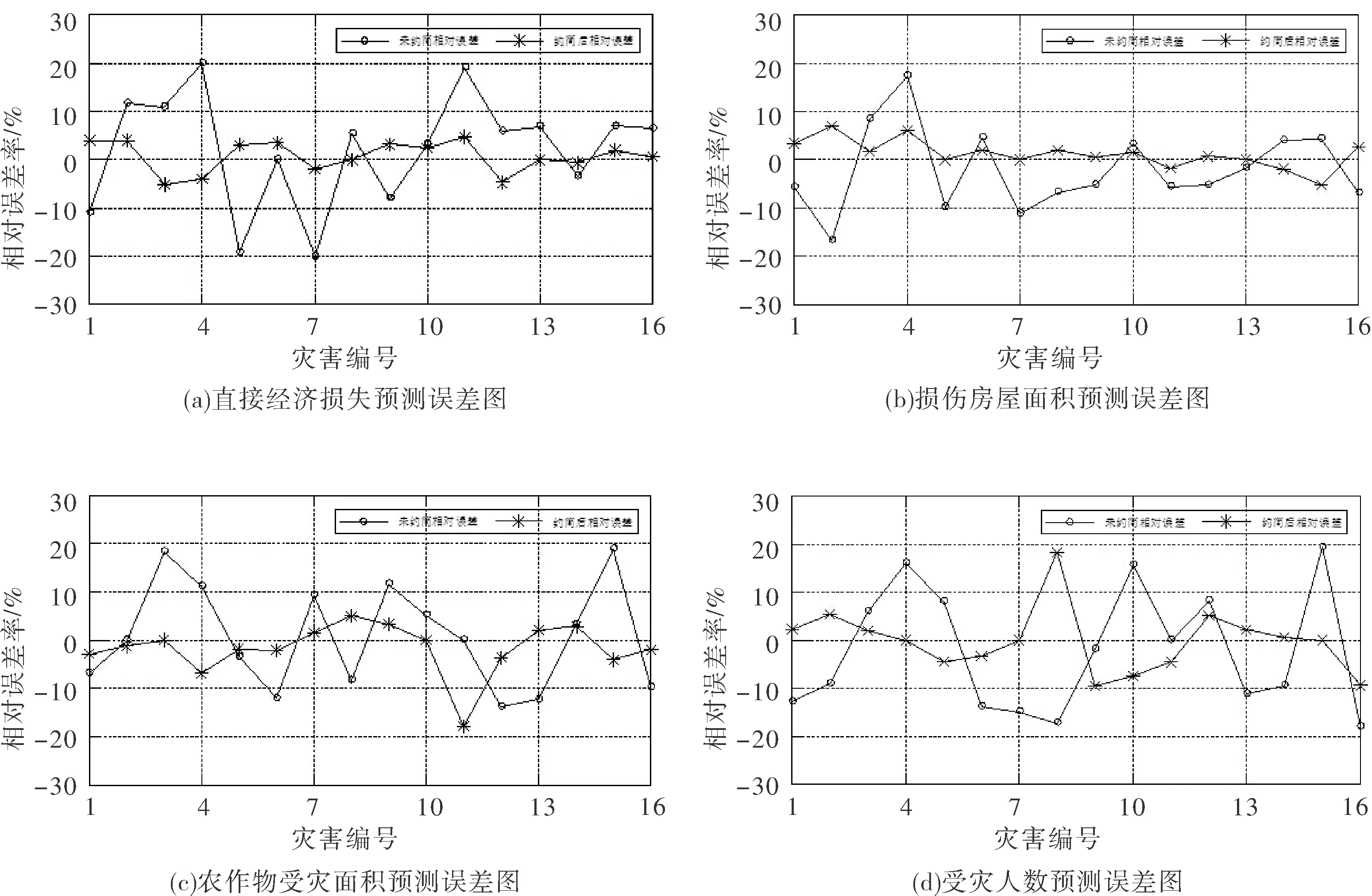
图4 模型预测结果误差图

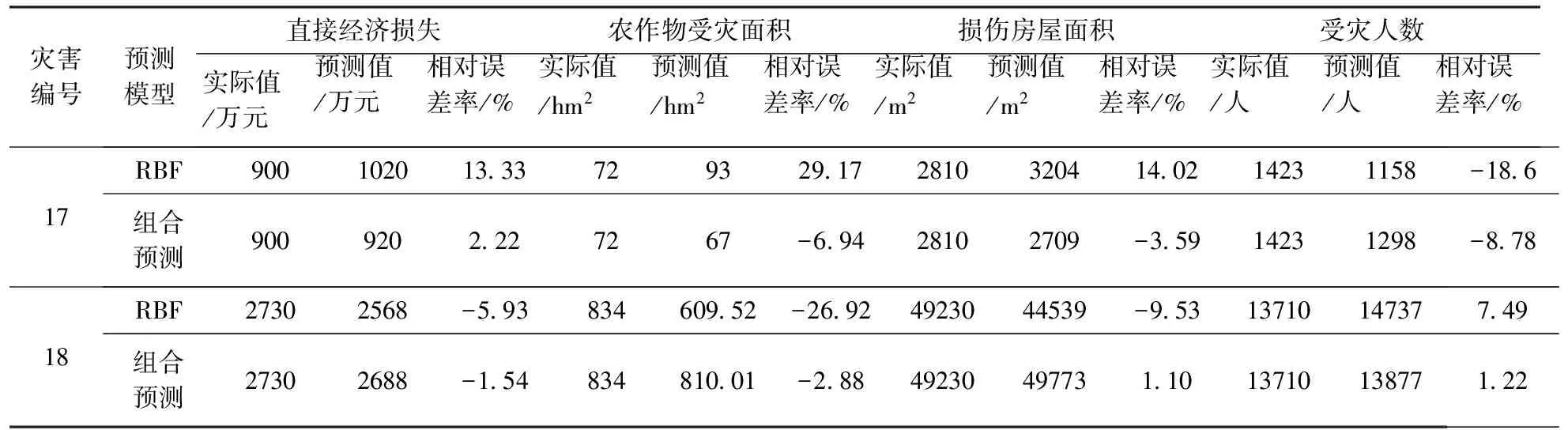
灾害编号预测模型直接经济损失农作物受灾面积损伤房屋面积受灾人数实际值/万元预测值/万元相对误差率/%实际值/hm2预测值/hm2相对误差率/%实际值/m2预测值/m2相对误差率/%实际值/人预测值/人相对误差率/%17RBF900102013337293291728103204140214231158-186组合预测9009202227267-69428102709-35914231298-87818RBF27302568-59383460952-26924923044539-9531371014737749组合预测27302688-15483481001-28849230497731101371013877122

注：组合预测是指经粗糙集约简后的RBF神经网络预测

因此经粗糙集模型对数据进行约简优化，可以明显改善RBF神经网络模型的预测精度和稳定性，降低了相对误差，预测结果比较理想。

4 结语

基于山洪灾害损失预测的理论实证研究不足，本文在参考其他自然灾害研究的基础上，利用粗糙集对预测指标体系进行优化约简，充分考虑致灾因子、孕灾环境、承灾体因素以及区域应灾能力等因素，建立山洪灾害损失预测指标体系，并采用RBF神经网络模型对1983-2013年神农架地区山洪灾害损失进行实证研究，结果表明：

(1) 经过粗糙集的约简计算，可以显著地剔除预测因子指标体系中无关因素，实现了对预测模型输入变量的优化，提高了模型的预测精度与可靠性。

(2) 根据独立样本试验可知，相比一般的RBF神经网络模型，基于粗糙集的RBF神经网络模型拟合精度较好，预测可靠性、稳定性较高，相对误差可以控制在3%左右，预测结果较为理想。

(3) 虽然神农架地区经济欠发达，灾害发生时损失风险较低，但考虑到其防灾减灾能力不足，频繁的灾害导致区域社会经济体系更为脆弱，“因灾致贫、因灾返贫”现象时有发生。因此，政府防灾减灾部门要做到对灾害损失及时预测，合理预估灾害程度的大小，以科学的布置防灾减灾工作、调配救灾人员和物资，将灾害损失降到最低。

进一步指出的是本研究仍存在以下待完善之处：未对灾害大小程度进行划分，未验证不同灾害程度下模型对灾害损失预测精度的影响；在预测过程中仍存在波动较大、误差相对较高的地方，需要进一步探讨与分析。

[1] 杜俊，任洪玉，张平仓，等. 大空间尺度山洪灾害危险评估的比较研究[J].灾害学，2016，31(3):66-72.

[2] 赵健，范北林. 全国山洪灾害时空分布特点研究[J]. 中国水利，2006(13)：45-47.

[3] 张明达，李蒙，戴丛蕊，等. 基于Flood Area模型的云南山洪淹没模拟研究[J]. 灾害学，2016，31(1)：78-82.

[4] 邹强，周建中，周超，等. 基于可变模糊集理论的洪水灾害风险分析[J]. 农业工程学报，2012，28(5)：126-132.

[5] 李龙伟. 西部山区城镇山洪灾害易损性评价[D].长沙：湖南科技大学，2013.

[6] 郭晓军，向灵芝，周小军，等. 高家沟泥石流和深溪沟泥石流灾害特征[J].灾害学，2012，27 (3)：81-85.

[7] 帅红，刘春平. 湖南省山洪灾害经济损失评价[J]. 防灾科技学院学报，2011，13(4)：81-85.

[8] 刘亚彬，刘黎明，许迪，等. 基于信息扩散理论的中国粮食主产区水旱灾害风险评估[J]. 农业工程学报，2010，26(8)：1-7.

[9] Matthieu Perrault, Philippe Gueguen, Alexandru Aldea, et al. Using experimental data to reduce the single-building sigma of fragility curves: case study of the BRD tower in Bucharest, Romania[J]. Earthquake Engineering and Engineering Vibration,2013,124:643-658.

[10]任玉峰，刘国东，周理，等. 基于证据理论和可变模糊集的成都市洪灾风险评估[J]. 农业工程学报，2014，30(21)：147-156.

[11]葛全胜，邹铭，郑景云，等. 中国自然灾害风险综合评估初步研究[M]. 北京：科学出版社, 2008.

[12]朱静，唐川. 城市山洪灾害易损性的RS和GIS分析[J]. 成都理工大学学报(自然科学版)，2008(1):61-67.

[13]Dushmanta Dutta,Srikantha Herath,Katumi Musiake. A mathematical model for flood loss estimation[J]. Journal of Hydrology,2003,2771:24-49

[14]殷洁，裴志远，陈曦炜，等. 基于GIS的武陵山区洪水灾害风险评估[J]. 农业工程学报，2013，29(24):110-117.

[15]周长锋，龚日朝，肖国安. 基于傅里叶级数的自然灾害损失预测模型研究——以湖南省自然灾害经济损失预测为例[J]. 中国安全科学学报， 2009,19(8):5-9,2.

[16]吉中会, 李宁, 吴吉东, 等. 区域洪涝灾害损失评估及预测的CART模型研究——以湖南省为例[J]. 地域研究与开发， 2012(6):106-110,144.

[17]陈香. 福建省洪涝灾害经济损失趋势分析[J]. 北华大学学报(自然科学版)， 2007(2):170-175.

[18]张颖超, 范金平, 邓华. 基于组合预测的浙江省台风灾害损失预测[J]. 自然灾害学报， 2013,22(6):223-231.

[19]王平, 黄河, 吴玮. 基于支持向量机的湖北省洪涝农业损失预测模型[J]. 湖北农业科学， 2014,53(18):4437-4440.

[20]刘少军，张京红，张明洁，等. DEA模型在山洪灾害危险性评价中的应用——以海南岛为例[J]. 自然灾害学报，2014，23(4)：227-234.

[21]Li K Z, Wu S H, Dai E F, et al. Flood loss analysis and quantitative risk assessment in China[J]. Natural Hazards,2012(63): 737-760.

[22]Jing Chen. Analysis on key problems of Mountain Torrent Disaster Loss Assessment System in Liaohe River Basin[C]// Wang Y, Jiang X, Yang M, Zhang D, Yi X, editors. Fifth International Conference on Graphic and Image Processing. Proceedings of SPIE. 90692014.

[23]Vozinaki A E K, Kourgialas N N, Karatzas G P. Estimating Flood Inundation and the Consequent Economic Losses in the Koiliaris River Basin in Crete, Greece[J]. Global Nest Journal， 2012;14(3):284-93.

[24]史培军. 再论灾害研究的理论与实践[J]. 自然灾害学报, 1996(4):8-19.

[25]章德武, 谌宏伟. 山洪灾害致灾因子分析与防治措施[J]. 中国水运(下半月刊), 2011,11(3):146-147.

[26]韩赜, 林孝松, 左倩云, 等. 山区镇域山洪灾害孕灾环境分区研究[J]. 重庆工商大学学报(自然科学版), 2014,31(6):82-89.

[27]李龙伟. 西部山区城镇山洪灾害易损性评价 [D].长沙：湖南科技大学, 2013.

[28]叶小岭, 梁伟, 邓华. 基于主成分分析及RBF神经网络的浙江省台风灾害损失预测[J]. 科技通报， 2014,30(9):13-19.

[29]Ghanbarpour M R, Saravi M M, Salimi S. Floodplain Inundation analysis combined with contingent valuation:implications for sustainable flood risk management[J]. Water resource management, 2014, 28(9): 2491-2505.

[30]Lepuschitz E. Geographic information systems in mountain risk and disaster management[J]. Appl Geogr，2015，63:212-220.

[31]刘兴杰,岑添云,郑文书,等. 基于模糊粗糙集与改进聚类的神经网络风速预测[J]. 中国电机工程学报,2014,34(19):3162-3169.

[32]高爽,冬雷,高阳,等. 基于粗糙集理论的中长期风速预测[J]. 中国电机工程学报,2012,32(1):32-37,21.

[33]鲍新中,张建斌,刘澄. 基于粗糙集条件信息熵的权重确定方法[J]. 中国管理科学,2009,17(3):131-135.

[34]杨鹏, 刘品杰, 张燕, 等. 基于RBF神经网络的改进多变量预测控制[J]. 控制工程， 2009,16(1):39-41,55.

Mountain Torrent Disaster Loss Prediction Research Based onRSs and RBF Neural Network：A Case Study on Shennongjia

LI Yichen, HE Yabo and WANG Yang

(SchoolofCivilEngineering,WuhanUniversity,Wuhan430072,China)

Shennongjia,locatedinthecentralandwesternmountainousareas,sufferedseriousdamagefrommountaintorrentinrecentyears.Themountaintorrentthreatensthecommunitiesusually,whichpushesthepeopleinworsecondition.Inthispaper,onthebasisofdisastersystemtheory,mountaintorrentdisasterlossindicatorsystemisestablishedinthevariedtopographyandpoorpeoplewidedistributionmountainousarea.Theindicatorsystemdividedinto4maincomponents,namelydisaster-inducingfactors,hazardinducingenvironment,physicalexposure,anddisasterreliefcapacity.Tooptimizingtheindicatorsystem,roughsettheoryisemployedtoanalyzeandoptimizetheinputindicators.ApplyingtheRBFneutralnetworkmodelbasedonthemountaintorrentdisasterhazard,propertydamageandcasualtieswerecomputedinShennongjia.Theresultsindicatedthat:Roughsetstheorycaneffectivelyextractthepredictorsthatcloselyrelatedtomountaintorrentdisasterandobservablyimprovespredictionaccuracy;TheRBFneuralnetworkmodelbasedontheroughsetstheoryhashigherpredictionaccuracycomparedwiththegeneralRBFneuralnetwork,ofwhichtherelativeerrorgenerallymaintainedatabout3%andtherelativeerrorcurveismoregentle.

mountaintorrentdisasters;lossforecasting;roughsets;RBFNeutralNetwork

10.3969/j.issn.1000-811X.2017.02.040.]

2016-07-29

2016-09-08

国家科技支撑计划课题“村镇区域综合防灾减灾信息系统研究及示范”(2014BAL05B00)

李祎琛(1993-)，女，河南平顶山人，硕士研究生，主要研究方向防灾减灾、可持续城市与区域发展. E-mail:li.yichen@whu.edu.cn

何亚伯(1956-)，男，湖北武汉人，教授，博士生导师，主要研究方向土木施工过程控制与信息化、防灾减灾、可持续城市与区域发展.E-mail:Hyb5610@163.com

X43；P648

A

1000-811X(2017)02-0227-08

10.3969/j.issn.1000-811X.2017.02.040

李祎琛，何亚伯，汪洋. 基于粗糙集RBF神经网络村镇山洪灾害损失预测研究——以神农架林区为例[J]. 灾害学，2017，32(2)：227-234. [LI Yichen, HE Yabo and WANG Yang. Mountain Torrent Disaster Loss Prediction Research Based on RSs and RBF Neural Network：a Case Study on Shennongjia[J]. Journal of Catastrophology，2017，32(2)：227-234.