加筋土挡墙屈服加速度与永久位移特性的拟动力法研究

袁卓亚，王卫山，上官甦，宋 彬，王 娟 ，何思明,6

(1.中国交通建设股份有限公司西北分公司，陕西 西安 710065；2.西安公路研究院，陕西 西安 710065；3.中国公路工程咨询集团有限公司，北京 100097；4.陕西交通建设集团公司，陕西 西安710065； 5.中国科学院山地灾害与地表过程重点实验室，四川 成都610041；6.青藏高原卓越中心，北京100101)

加筋土挡墙屈服加速度与永久位移特性的拟动力法研究

袁卓亚1，王卫山2，上官甦3，宋 彬4，王 娟5，何思明5,6

(1.中国交通建设股份有限公司西北分公司，陕西 西安 710065；2.西安公路研究院，陕西 西安 710065；3.中国公路工程咨询集团有限公司，北京 100097；4.陕西交通建设集团公司，陕西 西安710065； 5.中国科学院山地灾害与地表过程重点实验室，四川 成都610041；6.青藏高原卓越中心，北京100101)

加筋土挡墙具有良好的抗震性能，广泛应用于地震带边坡加固防护工程，但是其强震荷载下的力学行为仍未有全面认识。而传统的拟静力法和安全系数控制设计方法不能考虑地震加速度时程特征，与地震作用的真实情况不符。该文在极限分析上限定理的基础之上，结合Newmark理论，采用拟动力法，考虑地震加速度的时程变化特征，推导计算加筋土挡墙屈服加速度与永久位移的计算公式，研究地震作用下加筋土挡墙的动力响应。最后通过算例对该方法进行了验算，计算分析地震作用下加筋土挡墙的屈服加速度与永久位移，研究水平地震加速度和竖向地震加速度对加筋土挡墙稳定性的影响。并与传统的拟静力方法结果进行对比，研究结果显示：拟静力法设计的加筋土挡墙可能偏于保守，可能造成不必要的浪费，经济上不合理。

地震；加筋土挡墙；拟动力法；屈服加速度；永久位移

加筋土挡墙是由面板、填土中布置的筋材以及填料组成，通过筋土间的摩擦耦合作用，增加土体工程的稳定性的一种支档结构。因其施工简便、造型美观、工程造价低，并且具有一定的柔性，能够适应轻微变形，具有良好的抗震性能，特别是用于地震带边坡加固防护工程。尽管加筋土挡墙的抗震性能得到国内外学者的肯定[1-5]，但人们对于加筋土挡墙在强震荷载下的力学行为仍未有全面认识[6]。近年来，国外学者[7-10]等在室内开展了小比例尺加筋土挡墙振动台性能试验，但由于相似比问题难以解决，小型振动台模型试验成果难以全面反映大尺度加筋土挡墙的动力特性。现阶段加筋土挡墙的抗震设计通常采用的方法是拟静力学法结合极限平衡理论或极限分析理论。比如蒋建清[11]等采用拟静力法结合极限平衡理论研究了不同破坏模式条件下加筋土挡墙的稳定性分析；Nimbalkar等[2]采用水平条分法结合拟动力法研究了加筋土挡墙在地震荷载下的稳定性。然而极限平衡理论是建立在诸多假设条件之上，没有考虑屈服准则及流动法则，因此采用极限平衡法研究加筋土挡墙的稳定性存在一定的不足；Ali Porbaha[12]等以极限分析上限定理为基础，通过计算分析得出的一个边坡临界高度，并且计算结果能够与实验结果大体吻合；杨明等[13]以前人加筋土挡墙动力试验为依据，结合拟静力法以及极限分析上限定理推导出了加筋土挡墙在水平向地震荷载作用下产生的屈服加速度的表达式；赵炼恒等[14]研究了不同加筋模式下的边坡临界高度以及临界加筋强度计算公式，并认为忽略竖向地震荷载使得结果偏于不安全；程火焰等[15]通过非线性有限元法与室内试验相结合的方法分析了加筋土挡墙的抗震动力特性，得出地震动力对动似摩擦系数有显著影响。

强震带加筋土挡墙抗震设计通常采用传统的拟静力法和安全系数控制设计，这种设计方法没有考虑边坡工程的地震动力响应，忽略了地震加速度时程和边坡破坏模式的影响，与地震作用的真实情况不符。地震荷载是往复荷载，加筋土挡墙安全系数可能在几个时间段内低于1.0，但并不发生整体的破坏。加筋土稳定性取决于地震过程中边坡永久位移的累积，只要加筋土挡墙累计位移不超过临界值，加筋土挡墙不会产生整体垮体，只会产生部分永久变形，汶川8级地震灾区大量加固边坡加固结构调查也证明了这一点。基于边坡支挡结构永久位移控制设计理论已为国内外大多数学者所接受[16-19]。Richards[16]首次采用拟静力法研究了边坡支挡结构地震位移研究工作；Nadim等[20]根据耦合力、力矩平衡关系研究了重力式挡土墙的地震水平位移与倾斜；Ausilio[6]采用拟静力法研究了不同破坏模式下加筋土挡墙的屈服加速度与永久位移计算方法。拟静力法简单地将地震惯性力均匀地施加在边坡支挡结构上，没有考虑地震加速度的时程变化特征，不能合理反映边坡支挡结构在实际地震荷载下的动力响应，近年来，越来越多的国内外学者采用拟动力法研究边坡支挡结构的动力响应[21-25]。

本文在极限分析上限定理的基础之上，结合Newmark理论，采用拟动力法，同时考虑水平和竖向地震加速度的时程变化特征，推导计算加筋土挡墙屈服加速度与永久位移的计算公式，通过算例进行本方法的展示，计算分析地震作用下加筋土挡墙的屈服加速度与永久位移，揭示地震作用下加筋土挡墙动力响应，水平地震加速度和竖向地震加速度对加筋土挡墙稳定性的影响。并与传统的拟静力方法结果进行对比，为强震带加筋土挡墙抗震设计提供技术支撑。

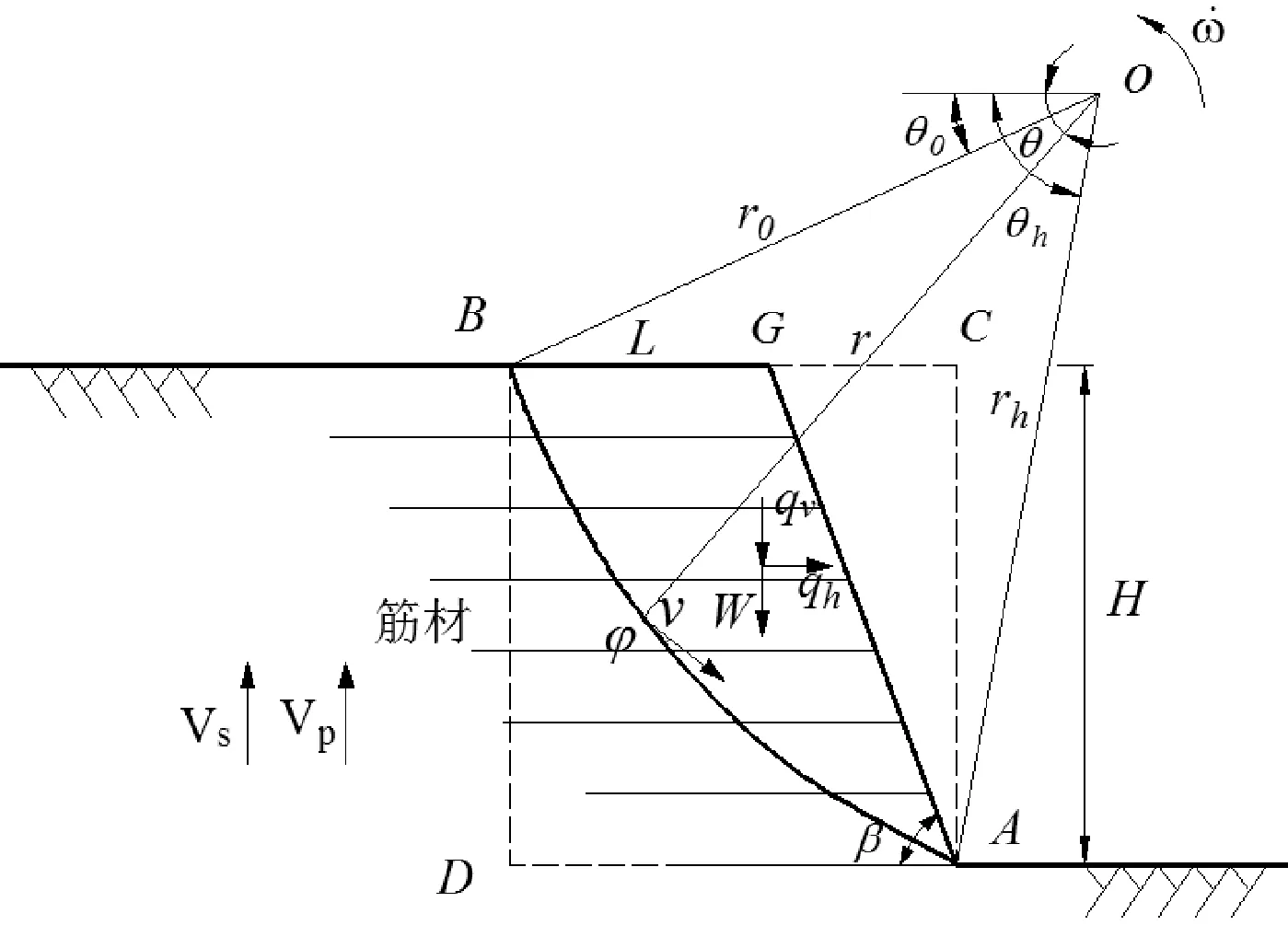
图1 加筋土挡墙永久位移拟动力法计算模型

1 基于拟动力法加筋土挡墙屈服加速度与永久位移计算方法

假设加筋土挡墙岩(土)体是各项同性的均质体，其破坏模式假设为旋转破坏，破裂面为对数螺旋形破裂面，如图1所示。整个坡体可看作是绕旋转中心O点转动的旋转机构。假设边坡高度为H，土体容重为γ，内摩擦角为φ，内聚力为c，水平加速度系数为kh，竖向加速度系数为kv，地震周期为T。 根据国内外学者对地震加速度的研究分析[23-25]，地震加速度沿着挡土墙高为正弦形式分布。水平地震加速度与竖直加速度分别是ah、av。假设挡土墙高度为H，则距离挡土墙顶面距离为z处的水平向地震加速度为：

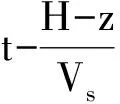
(1)

竖直方向地震加速度表达式为：

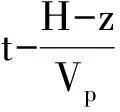
(2)

式中：地震剪切波速率为Vs，纵波的速率为Vp，G为土体剪切模量，ρ为土体密度，v为泊松比。则

1.1 地震荷载作用下加筋土挡墙外功率计算

加筋土挡墙外力所做功率包括两个部分：重力所做的功率以及地震力所做的功率。其中重力功率表示如下:

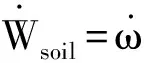
(3)

在计算水平向地震力时，直接对图1中的ABG求积分会比较复杂，因此把整个滑体分成ACG,ACBD以及ADB,分别计算三个部分对于旋转中心的功率，即可得水平地震力所做功率为：

(4)

选取ABCD为参考，并将其看作全部由土体组成，在距离墙顶z处，取水平微元进行水平向地震力的分析，可以得出水平微元的质量为：

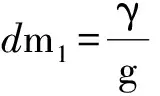
(5)

假设地震作用力的作用点在重心位置，则水平微元地震力到旋转中心的距离：

d1=(r0sinθ0+z)。

(6)

则ABCD对旋转中心所做的功率为：

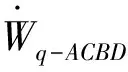
(7)

将式子(5)、(6)代入(7)，则可得出详细解：

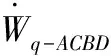
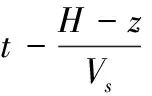
khr0γ{cosθ0-exp[(θh-θ0)tanφ]cosθh}[r0cos2πξ1sinθ0-

(8)

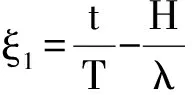
同理可得：

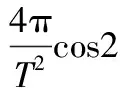
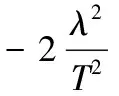
(9)

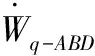
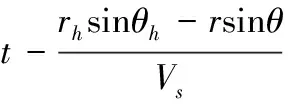
(10)

竖向地震力对滑体所做外力功率为：

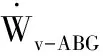
(11)

(12)

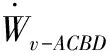
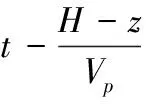
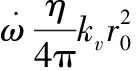
[(θh-θ0)tanφ]cos2θh}。

(13)

(14)

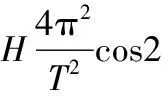
(15)

故加筋土挡墙在旋转模式破坏下外力所做的功率为：

(16)

1.2 地震荷载作用下加筋土挡墙内能耗散率

加筋土挡墙结构中，内部能量耗散率包括加筋筋材破坏导致的能量耗损率以及为了防止滑体滑动，土体粘聚力产生的能量耗损率。与拟静力法计算内能耗散率相同。

(17)

土体粘聚力产生的能量耗散为：

(18)

1.3 加筋土挡墙屈服加速度拟动力分析

当外力所作功率与内能耗散相等的时候，加固结构处于极限平衡状态，此时对应的地震加速度为屈服加速度，其表达式为：

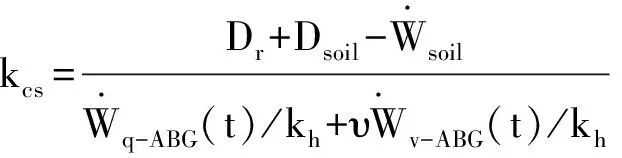
(19)

由式(13)可得安全系数为θ0，θh的函数，即：

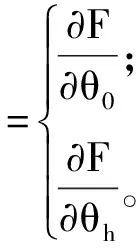
(20)

为了求得加筋土挡墙处于临界状态时对应的地震的屈服加速度系数，方程应满足如下约束条件：

(21)

对式(14)求最小值，即可得到相应的θ0，θh。

1.4 加筋土挡墙永久位移的拟动力分析

Newmark认为，在地震过程中，只有当地震的加速度超过屈服加速度时，结构才产生位移，当加速度小于屈服加速度时，结构是不产生位移的。对于本文给定的考虑地震加速度时程与位移的情况下，已知屈服加速度的值，则可计算出滑体的位移，计算公式如下：

(22)

绕旋转中心的转动角加速度a为：

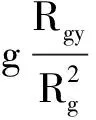
(23)

式中：a为滑体的转动角加速度；Rg为滑体中心到旋转中心的距离；k(t)为实际的地震加速度系数，kcs为地震屈服加速度系数；Rgv为Rg沿垂直方向的分量。

则转动速度v为：

(24)

转动角度ϑ为：

(25)

2 工程算例分析

2.1 静力条件下加筋土挡墙稳定性分析

取加筋土挡墙高度为H=10m，坡度β=60°, 重度为γ= 20kN/m3，加筋时单位界面上筋材拉伸强度k0=15kPa，水平地震加速度系数为kh=0时，即边坡在静力荷载条件下，开展不同土体粘聚力c(10～25kPa)和不同内摩擦角φ(25～35°)条件下加筋土挡墙稳定系数，不同土体粘聚力和不同坡度条件下对应的加筋土挡墙稳定安全系数。计算结果见图2、图3。

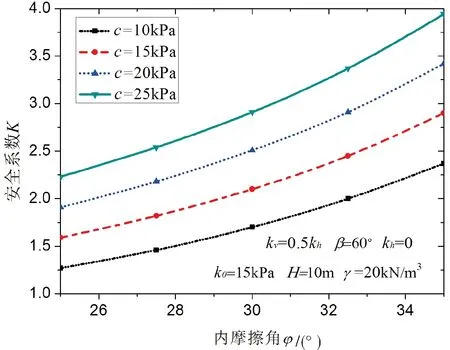
图2 内摩擦角与稳定系数的关系

由图2可知，随着土体内摩擦角以及粘聚力的增加，加筋土挡墙稳定性安全系数逐渐增大，当内摩擦角越大的时候，安全系数增大得越快。

由图3可知，随着边坡坡度的增大，加筋土挡墙稳定性安全系数呈减小趋势，并且呈现先加速减小后平缓减小。另外，加筋土挡墙稳定性安全系数随着粘聚力的增大边坡安全系数逐渐增大。

2.2 加筋土挡墙动力响应的拟静力分析

已知加筋土挡墙高H=10m，坡度β=60°, 重度为γ=20kN/m3，单位界面上筋材拉伸强度k0=15kPa，水平地震加速度系数分别为kh=0，0.1，0.2，0.3，kv=0.5 kh时，计算得出内摩擦角与安全系数的关系，如图4所示。

图3 坡度与稳定性安全系数的关系曲线

图4 不同地震加速度系数对应内摩擦角与安全系数的关系曲线

由图4中可以得出：当水平加速度系数相同的条件下，加筋土挡墙稳定系数随内摩擦角的增大而增大，当水平加速度系数越大，加筋土挡墙安全系数增加得越缓慢。

在其他参数相同的情况下，当k0=10kPa，kh=0.2，竖向地震加速度系数分别为kv=0，kv=0.5kh，kv=kh时，计算得到了不同内摩擦角对应的加筋土挡墙地震屈服加速度系数的大小(图5)。由图5中可以看出：当忽略竖向地震加速度时，整体的屈服加速度系数的值是偏大的，相比考虑竖向加速度，会使得实际工程将偏于不安全。并且当kv=μkh，μ值较小时，对屈服加速度系数的值影响不大，但是随着μ的增大，使得结果相差较大。

图5 内摩擦角与屈服加速度的关系曲线

为了研究不同筋材拉伸强度下，加筋土挡墙地震屈服加速度系数与边坡坡度之间的关系，选取内摩擦角φ=30°，在其他条件相同的情况下，得到了图6，由图6可知，在筋材拉伸强度是定值时，屈服加速度系数随着边坡坡度的增加呈近似线性减小的相关关系。屈服加速度的值越大说明加固边坡的抗震性能越好。

图6 边坡坡度与屈服加速度的关系曲线

当H=10m，c=15kPa，φ=25°，β=60, γ =20kN/m3，k0=10kPa时，可算出此时对应的屈服加速度系数为kcs=0.13。根据以上理论分析以及工程实例计算，可以得出了不同水平地震加速度系数对应的边坡潜在破裂面的形状(图7)。由图7可知，随着水平地震加速度系数值的增加，加筋土挡墙潜在破裂面的开口距离越远，形成的滑体规模越大。

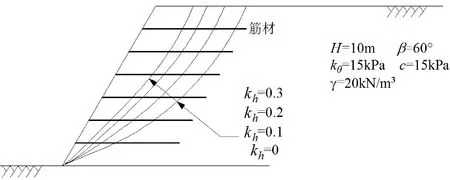
图7 不同水平加速度系数对应的加筋土挡墙潜在滑裂面形状

2.3 加筋土挡墙地震动力响应的拟动力分析

选取坡高H=12m，坡度β=60°, 重度为γ=20kN/m3，φ =30°，加筋条件下，单位界面上筋材拉伸强度k0=10kPa，竖向地震加速度系数kv=0，水平地震加速度系数分别为kh=0，0.1，0.2，时，一个周期内边坡的安全系数的变化(图8)。

由图8可知，加筋土挡墙在静力条件下的稳定系数为K=1.2，说明在没有地震荷载作用时，加筋土挡墙处于稳定状态。当水平地震加速度系数kh=0.1时，拟静力法计算得到的安全系数仅为K=0.9，而拟动力法计算得到的边坡安全系数在地震的有一个周期内是先减小后逐渐增大，最大的安全系数可达1.39，最危险时刻的安全系数为0.99。随着加速度系数的增加，t/T在0～0.3和0.8～1.0时段内，加筋土挡墙的稳定性安全系数是大于静力条件下对应的安全系数，并且水平加速度系数越大，边坡安全系数越高。而在0.3～0.8周期内，水平加速度系数越大，边坡安全系数反而越小。从由图8还可以看出，加筋土挡墙在地震作用下安全系数并不是一个定值，而是随着时间变化会不断变化，只在某一时段内会出现边坡安全系数小于1.0的情况。

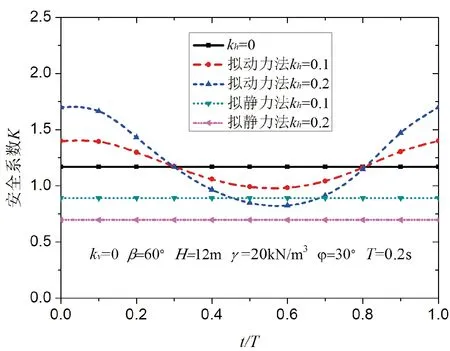
图8 一个地震周期内稳定系数的变化曲线

图9 不同竖向地震加速度与稳定系数的关系曲线

图9表示竖向地震加速度系数对加筋土挡墙稳定性安全系数的影响，从图中可知，竖向地震加速度系数对加筋土挡墙的稳定性的影响较小。图10表示不同内摩擦角对应的一个周期内加筋土挡墙稳定系数值的大小，由图可知，内摩擦角对加筋土挡墙稳定性安全系数有显著的关系。

图11为拟动力法和拟静力法计算得到的屈服加速度系数比较，从图11中可知，在相同条件下，拟动力法得出的屈服加速度系数的值大于拟静力法计算得到的屈服加速度值。因此按照拟静力法设计的加筋土挡墙偏于保守。

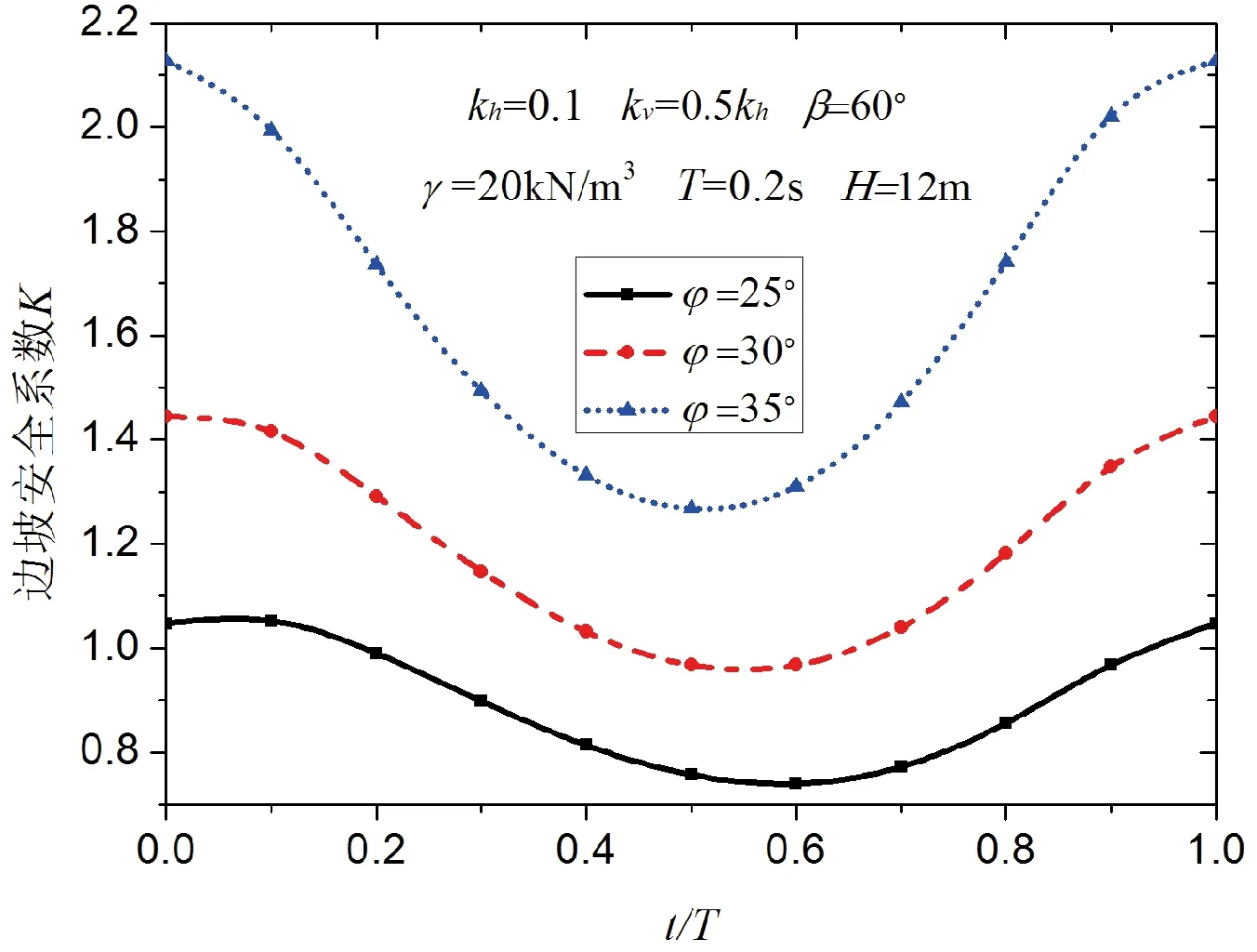
图10 不同内摩擦角与边坡安全系数的关系曲线

图11 两种方法对应的屈服加速度系数

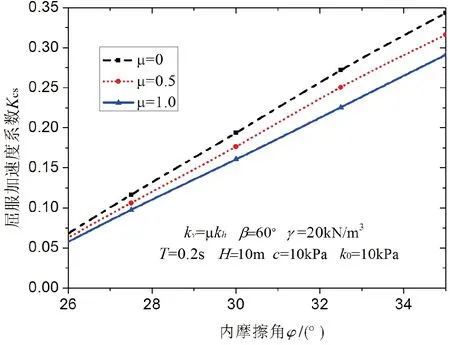
图12 竖向地震加速度对加筋土挡墙屈服加速度的影响

图12表示不同竖向地震加速度系数条件下加

筋土挡墙屈服加速度系数，从图中可知，竖向地震加速度系数的值越大，加筋土挡墙屈服加速度系数值越小，比不考虑竖向加速度系数的情况更加的符合实际，也使得结构更加的安全可靠。

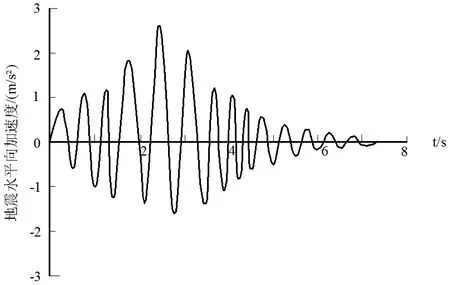
图13 模拟地震频谱

2.4 强震荷载下加筋土挡墙地震永久位移对不比较 为了比较拟静力法和拟动力法对加筋土挡墙地震永久位移计算结果的影响，我们根据成都地震台所测的汶川地震波数据进行分析，并结合当地地形、地质条件进行衰减推算出来的地震波(图13)。选取的计算参数见表1。

表1 计算参数表

H/mc/kPaφ/(°)k0/kPaβ/(°)γ/(kN/m3)101030106020

由给定的已知参数可求得此时对应的屈服加速度值，其中拟动力法得出加筋土挡墙最危险时刻对应的屈服加速度值为kcs=0.175, 拟静力法计算得出的屈服加速度值为kcs=0.118。根据以上分析，可以得出地震加速度系数超过屈服加速度系数的时段有三次，根据前文对永久位移的理论分析计算得到，拟静力法计算得出的水平距离可达16.9 cm，而运用动力学的方法得出的永久位移仅为4.34 cm，拟静力法计算得到的旋转角度为0.027 6 rad，动力法计算得出的旋转角度为0.012 8 rad (表2)。由此可见，运用拟静力学的方法设计得到的加筋土挡墙永久位移值大于拟动力法计算结果，在相同临界的永久位移阈值时，拟静力学计算结果偏于保守，而拟动力法计算结构更加符合实际。

表2 不同计算方法确定的加筋土挡墙地震永久位移累积值

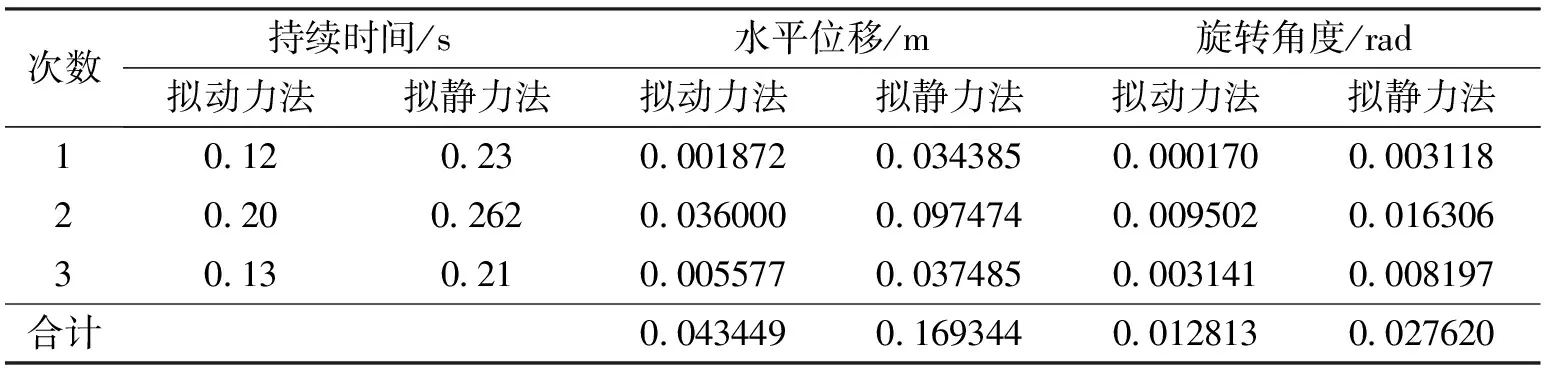
次数持续时间/s水平位移/m旋转角度/rad拟动力法拟静力法拟动力法拟静力法拟动力法拟静力法1012023000187200343850000170000311820200262003600000974740009502001630630130210005577003748500031410008197合计0043449016934400128130027620

3 结论

采用极限分析上限定理，结合拟动力法推导了加筋土挡墙屈服加速度与永久位移计算方法，研究了加筋土挡墙稳定系数与内摩擦角、坡度之间的定量关系；竖向地震加速度对加筋土挡墙稳定性的影响；比较了拟静力法和拟动力法速度对加筋土挡墙屈服加速度与永久位移计算结果的影响，并获得了以下结论：

(1)运用拟动力学法计算得出的加筋土挡墙安全系数在一个地震周期内随时间呈现先减小后增大的趋势。

(2)竖向地震加速度系数对加筋土挡墙地震永久位移有影响，证明在加筋土挡墙设计中不能忽略竖向地震加速度的影响，考虑竖向地震加速度系数相比不考虑竖向加速度系数使得结构偏于安全。

(3)拟静力法得到的加筋土挡墙地震永久位移值较拟动力法偏大，说明按照拟静力法设计的加筋土挡墙偏于安全；但另一方面，按照拟静力法设计的加筋土挡墙可能偏于保守，造成不必要的浪费，经济上不合理。

在实际工程应用中，受地形、地层、岩性以及地震加速度的影响，问题可能要复杂许多，在采用拟动力法分析加筋土挡墙的屈服加速度与永久位移时，要综合考虑实际地震加速度时程、加筋材料布置方式、填土材料性质的影响，计算方法与步骤与本文算例相同。

[1] Ling H I, Leshchinsky D, Perry EB. Seismic design and performance of geosynthetic-reinforced soil structures[J]. Geotechnique, 1997,47(5):933-52.

[2] S S Nimbalkar, D Choudhury and J Mandal. Seismic stability of reinforced soil wall by pseudo-dynamic method [J].Geosynthetics international, 2006,13(3)111-120.

[3] LIU Huabei, WANG Xiangyu, SONG Erxiang. Reinforcement load and deformation mode of geosynthetic-reinforced soil walls subject to seismic loading during service life[J].Geotextiles and Geomembranes, 2011,29: 1-16.

[4] LIU Huabei, YANG Guangqing, LING HoeI. Seismic response of multi-tiered reinforced soil retaining walls[J]. Soil Dynamics and Earth quake Engineering, 2014,61:1-12.

[5] Lee K Z Z, CHANG N Y. Predictive modeling on seismic performances of geosynthetic-reinforced soil walls[J]. Geotextiles and Geomembranes,2012,35: 25-40.

[6] Ausilio E, Conte E, Dente G.Seismic stability analysis of reinforced slopes[C]//Soil Dynamics and Earthquake Engineering 19,2000:159-172.

[7] Koga Y, Washida S. Earthquake resistant design method of geotextile[C]// Proceedings of the International Symposium on Earth Reinforcement,Rotterdam, 1992:255-314.

[8] Yamanouchi T, Fukuda N. Design and observation of steep reinforced embankments[C]// Proceedings of the Third International Conference on Case Histories in Geotechnical Engineering, St. Louis, MO, 1993:1361-1439.

[9] G Madhavi Latha, A Murali Krishna. Seismic response of reinforced soil retaining wall models: Influence of backfill relative density[J]. Geotextiles and Geomembranes, 2008, 26 :335-369.

[10]M Sabermahani, A Ghalandarzadeh, A Fakher. Experimental study on seismic deformation modes of reinforced-soil walls[J]. Geotextiles and Geomembranes,2009, 27: 121-134.

[11]蒋建清，杨果林. 加筋土挡墙地震稳定性分析的水平条分方法[J]. 中国铁道科学,2009(1): 36-40.

[12]Porbaha A, Zhao A G, Kobayashi M, et al. Upper bound estimate of scaled reinforced soil retaining walls[J]. Geotextiles and Geomembranes, 2000, 18(6): 403-413.

[13]杨明，吴德伦，言志信. 加筋土挡墙抗震分析中的屈服加速度[J]. 岩石力学与工程学报, 2002(5): 728-731.

[14]赵炼恒，李亮，杨峰，等. 加筋土坡动态稳定性拟静力分析[J]. 岩石力学与工程学报,2009(9): 1904-1917.

[15]程火焰，周亦唐，钟国强. 加筋土挡土墙地震动力特性研究[J]. 公路交通科技, 2004(9): 16-20.

[16]Richards R, Elms D G. Seismic behavior of gravity retaining walls[J]. J Geotech Eng Div ASCE,1979,105(4):449-513.

[17]B Munwar Basha, G L Sivakumar Babu. Computation of sliding displacements of bridge abutments by pseudo-dynamic method[J]. Soil Dynamics and Earthquake Engineering,2009,29:103-120.

[18]HE Siming, OUYANG Chaojun, LUO Yu. Seismic stability analysis of soil nail reinforced slope using kinematic approach of limit analysis[J]. Environ Earth Sci,2012, 66:319-351.

[19]LI Xinpo, WU Yong, HE Siming. Seismic stability analysis of gravity retaining walls[J]. Soil Dynamics and Earthquake Engineering,2010,30: 875-962.

[20]Nadim F, Whitman R R. Seismically induced movement of retaining walls[J]. J Geotech Eng ASCE,1983; 109 (7):915-946.

[21]Sreevalsa Kolathayar, Priyanka Ghosh. Seismic active earth pressure on walls with bilinear backface using pseudo-dynamic approach[J]. Computers and Geotechnics,2009, 36 : 1229-1352.

[22]Sanjay Nimbalkar, Deepankar Choudhury. Sliding stability and seismic design of retaining wall by pseudo-dynamic method for passive case[J]. Soil Dynamics and Earthquake Engineering,2007,27:497-547.

[23]Syed Mohd Ahmad, Deepankar Choudhury. Pseudo-dynamic approach of seismic design for waterfront reinforced soil-wall[J]. Geotextiles and Geomembranes,2008, 26: 291-321.

[24]Debarghya，Chakraborty, Deepankar Choudhury. Sliding stability of non-vertical waterfront retaining wall supporting inclined backfill subjected to pseudo-dynamic earthquake forces[J]. Applied Ocean Research,2014,47: 174-186.

[25]Sima Ghosh. Pseudo-dynamic active force and pressure behind battered retaining wall supporting inclined backfill[J]. Soil Dynamics and Earthquake Engineering,2010,30: 1226-1349.

附录：

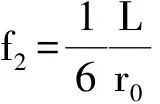
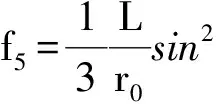
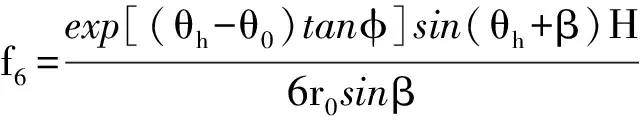
Computation of Sliding Displacements of Reinforced Soil Wall by Pseudo-dynamic Method

YUAN Zuoya1, WANG Weishan2, SHANGGUAN Su3, SONG Bin4,WANG Juan5and HE Siming5, 6

(1.ChinaCommunicationsConstructionCo.,Ltd.NorthwestBranch,Xi’an710065,China; 2.Xi’anHighwayResearchInstitute,Xi’an710065,China; 3.ChinaHighwayEngineeringConsultantsCo.,Ltd,Beijing100097,China; 4.ShaanxiProvinceTransportationConstructionGroupCo.,Ltd,Xi’an710065,China; 5.KeyLaboratoryofMountainHazardsandSurfaceProcess,ChineseAcademyofScience,Chengdu610041,China; 6.CASCenterforExcellenceinTibetanPlateauEarthSciences,Beijing100101,China)

Reinforcedsoilwallhassuperaseismicperformance,whichiswidelyusedinslopereinforcementengineeroftheseismiczones,butthemechanicalbehaviorundertheearthquakeloadshaven’tafullyunderstanding.Thetraditionalpseudostaticmethodandfactorofsafetycontroldesignmethodcan’tconsiderthetimehistorycharacterofseismicacceleration,anditisinconsistenttotherealseismicaction.Inthisstudy,basedonthekinematictheoremoflimitanalysistheseismic,combinedwiththeNewmarktheory,usingthepseudo-dynamicmethodtoconsiderthetimehistorycharacterofseismicacceleration,theexpressionsoftheyieldaccelerationandthepermanentdisplacementofreinforcedsoilwallisderived.Wethenanalyzethedynamicresponseofthereinforcedsoilwall.Atlast,acaseisusedtoillustratethemethod.Thecriticalseismicyieldaccelerationcoefficientandtheseismicpermanentdisplacementofreinforcedsoilwallunderseismicloadingarecalculated.Meanwhile,theeffectofthehorizontalseismicaccelerationandverticalaccelerationeffectonthestabilityoftheslopewithreinforcedsoilwallisanalyzed.Thecomparisonismadewiththepseudo-staticmethod.Theresultshasshownthatthepseudo-staticmethodmaygiveaconservativedesignforreinforcedsoilwall,itmaycauseunnecessarywasteandnoteconomically.

seismic;reinforcedsoilwall;pseudo-dynamicmethod;yieldaccelerationcoefficient;permanentdisplacement

2016-10-09

2017-01-19

NSFC-ICIMOD国际合作基金(41661144041)；交通运输部科技项目(2014364J03090)

袁卓亚(1971-)女，汉族，陕西西安人，博士，高级工程师，主要从事公路与桥梁工程方面研究. E-mail：791027696@qq.com

何思明(1968-)男，汉族，四川蓬溪人，博士，研究员，博士生导师，主要从事山地灾害形成机制研究. E-mail: hsm@imde.ac.cn

10.3969/j.issn.1000-811X.2017.02.004.]

TU43；X43

A

1000-811X(2017)02-0018-08

10.3969/j.issn.1000-811X.2017.02.004

袁卓亚，王卫山，上官甦，等. 加筋土挡墙屈服加速度与永久位移特性的拟动力法研究[J]. 灾害学，2017，32(2)：18-25. [YUAN Zuoya, WANG Weishan, SUN Yunfu,et al. Computation of Sliding Displacements of Reinforced Soil Wall by Pseudo-Dynamic Method[J]. Journal of Catastrophology，2017，32(2)：18-25.