金属埋地管道腐蚀泄漏及大气扩散过程推理模型研究*

左　哲, 王　敏, 姚志强, 孙恩吉

(1.中国安全生产科学研究院，北京 100012；2.国家安全生产监督管理总局信息研究院，北京 100029)

0　引言

埋地金属管道腐蚀泄漏过程随机性较大，表现在腐蚀致因因素较多且相互关联导致腐蚀失效过程具有较大复杂性，以及受环境条件影响下泄漏范围的不确定性。腐蚀失效过程研究应将重点放在埋地金属管道腐蚀致因因素集的构建和因子之间耦合作用对腐蚀风险的影响，建立金属管道腐蚀失效全过程的事件链。泄漏后果预测的难点在于外界环境随机变化导致扩散范围差异性较大，基于统计数据计算得到的泄漏范围只是众多可能后果的平均值，应分析环境条件概率分布与扩散范围之间的关联，研究扩散后果的概率分布特征。

管道腐蚀失效概率计算方法主要包括失效概率修正法和结构可靠性计算法[1]。前者基于管道失效统计数据计算得到管道失效基本概率，再根据实际情况进行修正[2]；后者是在给定管道输送条件下，根据强度—应力理论计算得到管道失效概率值[3]。肯特危险指数法也是较为常见的计算方法，该方法是通过计算管道危险指数用以描述管道失效风险[4]。其他管道失效概率计算方法还包括故障树[5]、BP神经网络[6]、层次分析[7]和模糊数学[8]等。在泄漏扩散范围预测方面，常用的评价模型包括高斯烟羽模型、火球热辐射伤害模型、蒸气云爆炸等[9]。近年，基于个人风险和社会风险值的风险评估模型也用于事故潜在危险区域分析[10]。

综上所述，国内外对管道腐蚀失效及泄漏扩散风险研究文献较多。以下将研究重点放在埋地金属管道腐蚀失效事件链的构建，以及环境条件随机变化情况下扩散后果概率分布特征的研究上。将基于贝叶斯网络图构建管道腐蚀失效事件链，网络中各节点代表腐蚀影响因子，采用条件概率量化影响因子对下一级事件的影响，通过贝叶斯概率计算得到最终腐蚀失效概率；研究环境条件因子的概率分布特征并匹配相应的概率分布函数，通过蒙特卡罗模拟方法计算得到扩散后果的概率分布图。

1　埋地金属管道腐蚀失效的贝叶斯网络构建

1.1　网络节点变量及结构确定

埋地金属管道腐蚀失效过程一般包括金属管道内腐蚀、外腐蚀、腐蚀防护措施失效、泄漏等4部分。研究上述4部分各自影响因子和相互关联，构建反映腐蚀失效过程的贝叶斯网络，如图1所示。贝叶斯网络是由节点和有向弧线组成的1个有向无环图。每个节点代表腐蚀过程的影响因子，其类型为离散型变量，网络结构关系代表了各因子之间的独立和条件独立关联，弧线代表了影响因子之间的依赖关系，即上一事件是下一事件的双亲或直接前驱[11]。如图1所示，埋地金属管道的腐蚀形式包括内腐蚀与外腐蚀2种，其中，内腐蚀事件的父节点包括输送介质腐蚀和内防腐措施失效等2方面；内防腐措施包括注入缓蚀剂、内防腐涂层和管道清管等3方面措施；外腐蚀的父节点包括土壤具有腐蚀性、管线年限长、杂散电流腐蚀和阴极保护、管道包覆层等外防腐措施失效4个方面[12]。外防腐蚀技术主要包括外防腐包覆层和阴极保护等2方面。管道腐蚀失效的形式，主要考虑了穿孔、断裂2种。

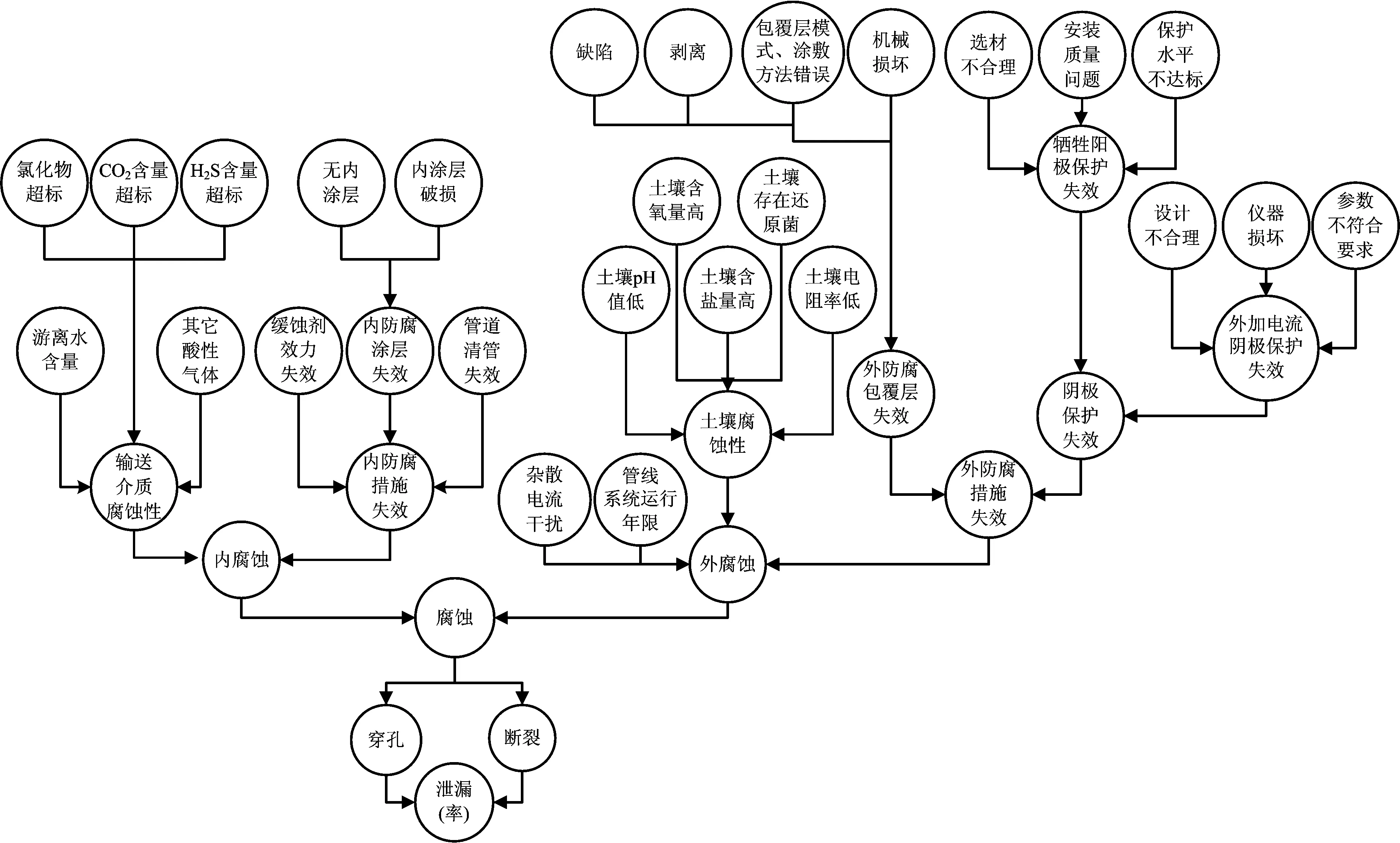
图1　埋地金属管道腐蚀失效贝叶斯网络Fig.1　Buried metal pipeline corrosion failure Bayesian

1.2　节点变量离散化

1.2.1输送介质腐蚀性及防腐措施

以20号无缝钢管为例，输送介质中主要腐蚀物包括CO2、氯化物、H2S、游离水以及其他酸性气体， 输送介质内腐蚀变量离散状态值，如表1所示。

表1　输送介质内腐蚀变量离散值状态值

1.2.2埋地金属外腐蚀及防腐措施

埋地金属管道外腐蚀主要是电化学腐蚀，金属管道外腐蚀变量离散状态值，如表2所示。考虑到硫酸盐还原菌的活动会加速金属腐蚀，将“土壤存在还原菌”节点状态设定为管壁硫化铁层是否存在。土壤的含氧量决定于土壤的透气性，“土壤的含氧量”节点状态用土壤的密实程度表示。

表2　埋地金属管道外腐蚀变量离散状态值

1.3　父子节点间条件概率设定

埋地金属管道腐蚀失效贝叶斯网络反映了导致管道腐蚀失效各节点变量间的概率依赖关系。为了研究父节点状态对子节点概率的影响，应确定每个节点与父节点之间的条件概率分布表(conditional probability table, CPT)。由于受到统计数据完整性的限制，难以对每1节点变量均给出准确的先验概率值。该概率反映了父节点状态值对子节点概率变化趋势的影响，满足因果关系合理性和可比性2方面要求。以“牺牲阳极保护失效”节点为例，条件概率表如表3所示。可见，“牺牲阳极保护失效”节点的3个父节点均具有2种状态值，即“是，否”，对应“牺牲阳极保护失效”共有8种条件概率。条件概率设定原则为：3个父节点的权重相同；当3个父节点同时出现问题，即状态值均为“Yes”，则“牺牲阳极保护失效”的条件概率为0.9；当其中任意2个的状态值为“Yes”时，“牺牲阳极保护失效”的条件概率为0.7；当仅有1个的状态值为“Yes”时，“牺牲阳极保护失效”的条件概率为0.5；当3个的状态值均为“No”时，“牺牲阳极保护失效”的条件概率为0.3。

表3　“牺牲阳极保护失效”节点条件概率

1.4　管道腐蚀过程节点敏感性分析

后验概率受节点变量在网络结构中的位置、条件概率分布以及节点变量先验概率的影响。以外腐蚀为例，通过推理可知土壤腐蚀性、外防腐措施、杂散电流情况以及管道年限均对管道外腐蚀概率有所影响。表4给出了土壤条件对土壤腐蚀性和管道外腐蚀程度影响的推理结果，表中未列出节点变量均采用其先验概率值。

表中给出的土壤腐蚀性和外腐蚀风险值是在其它节点变量采用先验概率条件下计算得到的，此时对应外防腐措施失效的概率为0.560 8。以土壤含盐量为例，当外防腐措施状态取值改变时，管道外腐蚀风险值，如表5所示。

表4　管道外腐蚀失效推理敏感性分析

表5　土壤含盐量、外防腐措施状态对管道外腐蚀风险影响

外腐蚀风险随土壤含盐量和外防腐措施是否失效状态的改变而不同，推理结果与实际相符。

2　管线泄漏后扩散范围蒙特卡罗法模拟

2.1　输气管线压力降及扩散模型

由于受到输送压力、泄漏速度、大气扩散条件等因素影响，输气管线泄漏后危险区域范围具有不确定性。输气管线质量流速和压力如式(1)和式(2)[14]：

(1)

(2)

式中：Qp气体输送速率，kg/s；P0为输气管起点压力(绝)，Pa；Pe为泄漏处压力(绝)，Pa；ρ0为气体初始密度，kg/m3；fF为范宁摩擦系数；L为泄漏点位置，m；u为气体流速，m/s；d为管道内径，m。

在泄漏点处，由于介质输送压力的作用，天然气的内能在从小孔泄漏或者扩散出去时转化为动能，在这一过程上气体密度、压力和温度均发生变化，通过泄漏口的质量速率为：

(3)

式中：Qh为气体管道泄漏速率，kg/s；CD为气体排放系数；A为开孔面积，mm2；γ为气体绝热指数。

2.2　泄漏气体土壤渗透模型

泄漏气体在土壤中的扩散过程研究主要包括数值模拟和建立解析方程2种方法。前者多假设土壤为标准多孔介质材料，将气体扩散过程所受到阻力转化为分布在流体上的阻力，通过建立气体扩散控制方程进行数值求解[15]，相对数值模拟方法，国内解析模型研究相对较少[16]。李雪洁采用达西定律来描述气体在土壤中的扩散过程，在计算得到管道的泄漏速率的基础上，根据渗透速度公式推导得到地表出口气体渗透速度，进一步积分得到埋地管道泄漏地表流量的数学表达式[17]：

(4)

式中：QB为埋地管道泄漏处地表出口流量，kg/s；k为土壤的固有(绝对)渗透系数，cm/s；μ为气体粘度，Pa·s；AB为管道泄漏处地表出口面积，m2；A0为管道泄漏口面积，m2；h管道埋深，m；P0为大气压，Pa。

2.3　泄漏气体大气扩散模型

天然气在大气条件下扩散过程属于中性浮力烟羽模型，采用地面处高斯烟羽模型计算空间任1点污染物浓度：

(5)

2.4　输送压力和环境风速概率分布特征

泄漏模型变量中增压站出站压力P0、气体排放系数CD和环境风速在实际中变化较大，因此需对该3个变量确定概率分布函数。首先，天然气在管道内输送过程中受到管径、输送距离等因素影响压力、温度均在不断变化，因此假设增压站出站压力符合正态分布规律。

(6)

式中：μ为平均压力，Pa；σ为标准差，Pa，取值为天然气增压站出站平均压力的20%。

由于管道断裂后开口形状、尺寸不一，导致气体排放系数具有一定的随机性。一般认为，当雷诺数大于100、开口为圆形时，CD取值0.65；当管道完全断裂时，气体排放系数CD取值1。因此，假设气体排放系数CD符合均匀分布，取值范围为0.65～1。

采用双参数威布尔分布函数来描述风速分布规律，其概率密度函数如式(7)所示[18]。

(7)

式中：c为平均风速，m/s；k为形状参数，标准形状参数可取值为2；v为10 min平均风速，m/s。

2.5　蒙特卡罗法模拟过程

蒙特卡罗模拟根据已知模型变量的概率分布进行随机取值，通过多次模拟得到多组模型预测结果，然后对预测值进行统计得到事件后果概率分布特征[19]。蒙特卡罗模拟过程为：根据随机选取1组模型变量，其中随机变量取值由概率密度函数随机产生(如风速)；将变量值代入已建立的模型进行模拟计算并记录模拟结果。按照上述方法多次进行抽样计算，对重复计算得到的多组(一般模拟次数为20 000次)预测结果进行统计，得到危险区域范围的概率估计值。

3　模型应用

3.1　评估对象条件设置

对华北地区某投产15a的天然气长输管道1处埋设地点的土壤腐蚀性进行测量[20]，测得该处土壤电阻率小于500 Ω·cm(属于低电阻率、强腐蚀性)、pH值大于7且小于8(中碱性、弱腐蚀性)、氧化还原电位大于400 mV(土壤还原性弱、不利于硫酸盐还原菌生长、弱腐蚀性)、Cl-离子含量处于0.002%～0.012%之间(弱腐蚀性)、接近干燥沙土(透气性好、含水量低、弱腐蚀性)。初步判断该地区土壤腐蚀性较弱，但不排除在靠近农舍或水井局部地区腐蚀性增大的可能性。管道输送介质天然气属于二类[21]，硫化氢≤20 mg/m3(弱腐蚀性)、二氧化碳≤3%(弱腐蚀性)。管道相关参数如下：管径525 mm，长300 km、泄漏点距增压站距离10 km、出站工作设计压力为6 MPa，全线采用了干空气干燥技术。当地常年平均风速为6 m/s，风向为西北风。

3.2　管道泄漏可能性评估分析

上述条件对土壤腐蚀性、天然气分类，管道施工质量等情况都进行了基本描述，但并未对投产后管道内(外)部防腐措施有效性进行详细说明。通过贝叶斯计算，得到土壤具有强腐蚀性的概率为0.300 0，弱腐蚀性的概率为0.700 0；输送介质天然气具有强腐蚀性的概率为0.310 0，而弱腐蚀性的概率为0.690 0。可见，对土壤和输送介质腐蚀性推理结果与凭经验直观判断结论较为相符。分析“牺牲阳极保护”和“管道清管”等2个措施状态对管道腐蚀乃至泄漏概率值进行分析，结果如表6所示。

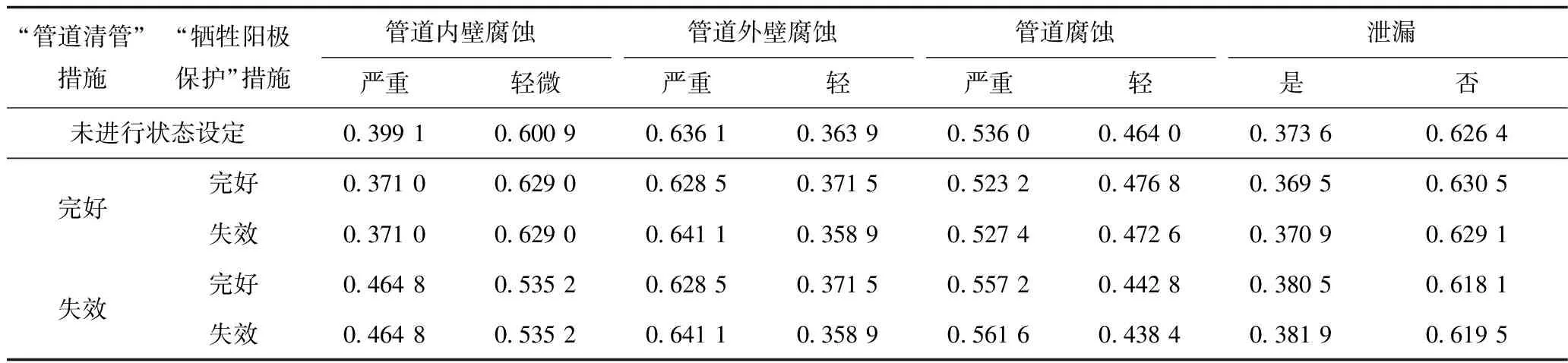
表6　防腐措施对腐蚀泄漏可能性分析

在未对防护措施进行设定的情况下计算得到管道内壁出现严重腐蚀的概率为(0.399 1)小于发生轻微腐蚀的概率(0.600 9)；但由于投产时间达15 a，管道外壁出现严重腐蚀的概率为(0.636 1)大于发生轻微腐蚀的概率(0.363 9)；管道总的严重腐蚀概率达0.536 0；发生泄漏的概率为0.373 6。当“管道清管”和“牺牲阳极保护”2方面措施均为完好状态时，管道内壁出现严重腐蚀的概率降为0.371 0，外壁出现严重腐蚀的概率降为0.628 5，管道总的严重腐蚀概率降为0.523 2，随之泄漏概率降为0.369 5。当“管道清管”状态完好和“牺牲阳极保护”措施失效时，对管道内壁腐蚀概率未造成影响，而外壁出现严重腐蚀的概率上升为0.641 1，管道总的严重腐蚀概率上升为0.527 4，随之泄漏概率上升为0.370 9。反之，当“管道清管”状态为失效和“牺牲阳极保护”措施完好时，对管道外壁腐蚀概率未造成影响，而内壁腐蚀概率均有所提高，则管道总的严重腐蚀概率和泄漏概率也随之上升。

3.3　参数抽样结果统计

基于上文对天然气长输管道泄漏及扩散模型中不变参数及随机参数分布形式的探讨，参考国内管道运行工况，模型中不变参数和可变参数分布函数的设置如表7，8所示。

表7　泄漏燃气扩散蒙特卡罗模拟不变参数设置情况

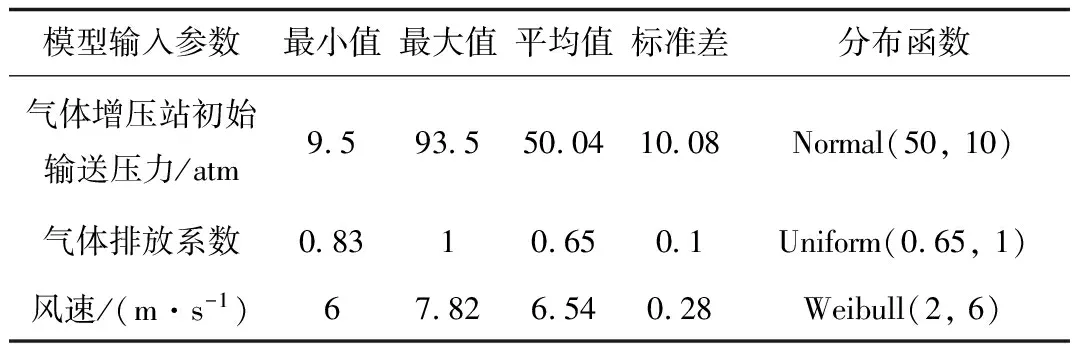
表8　泄漏燃气扩散蒙特卡罗模拟可变参数随机取值情况

表7所列模型参数为天然气和输送管道的物理属性变化幅度不大，因此在蒙特卡罗模拟随机取值时上述模型参数保持不变。考虑到气体增压站初始输送压力会随用气量和地质条件发生变化，设出站工作设计压力为50 atm，符合正态分布函数Normal(50, 10)。由于管道裂口形状对气体排放系数存在较大影响，将裂口处气体排放系数设为在0.65～1随机取值，符合均匀分布Uniform(0.65, 1)。采用土壤渗透模型计算埋地管道泄漏处地表出口流量，假设土体为连续、均匀、各向同性的干燥土壤且土体渗透率不变，泄漏气体不与土体发生任何化学反应。泄漏气体以漏斗状向地表扩散，到达在表出口时流速降低、出口面积变大，因此地表出口气体流量与管道泄漏口处流量基本一致。当地风速的取值为常年平均风速6 m/s，并符合威布尔分布Weibull(2, 6)。表8所示为对可变参数经20 000次模拟后状态值抽取结果的统计。

3.4　泄漏扩散区域范围计算

对上述管段进行蒙特卡罗模拟，得到管道破裂后泄漏质量流速和下风向天然气爆炸危险区域直方图，如图2，3所示。经计算得到，该管段发生天然气泄漏事故后泄漏质量速率符合正态分布，平均值为134.07 kg/s，标准差为19.18，泄漏最大质量速率可达141.63 kg/s，最小速率为68.29 kg/s。其中泄漏速率处于130～150 kg/s范围内速率所占频率总计达0.49。图3给出了天然气泄漏后下风向处于爆炸极限的危险区域范围最远点距离。由于每次模拟计算中泄漏速率及风速不同，因此下风向最远危险点范围也发生变化。可知，最远点距离平均值为190.44 m，标准差为14.47，其中最远距离可达240.62 m，最近距离也达到为134.82 m。其中，最远点距离范围处于(180～185 m)至(200～205 m)各组距内对应频率均达0.1以上，并且总计频率达0.62。

图2　泄漏质量速率直方图Fig.2　Histogram of leak quality rate

图3　下风向爆炸危险区域直方图Fig.3　Histogram of downwind explosion danger zone radius

4　结论

1)由于输送介质和土壤腐蚀性、防腐措施有效性和大气条件多方面因素的差异，导致埋地金属管道腐蚀泄漏过程、气体扩散范围具有较大的不确定性。

2)将贝叶斯网络方法用于埋地金属管道腐蚀泄漏过程推理研究，可以对演化过程各中间事件的关联进行分析，对泄漏可能性进行量化评估。

3)将蒙特卡罗模拟方法用于泄漏后扩散范围计算，使用概率密度函数表示泄漏扩散过程影响因素的不确定性，得到泄漏危险区域范围的概率分布特征。

4)将贝叶斯网络方法和蒙特卡罗模拟方法相结合，可以充分利用二者在处理不确定性问题上的优势，对输气管道腐蚀泄漏风险进行评估。

[1]黄小美, 李百战, 彭世尼，等. 燃气管道失效概率评估方法研究[J]. 石油学报, 2010, 31 (4)：664-667.

HUANG Xiaomei, LI Baizhan, PENG Shini，et al. Assessment methods of failure probability on gas pipelines[J]. Acta petrolei sincic, 2010, 31 (4)：664-667.

[2]靳书斌, 郑洪龙, 侯磊，等. 高压燃气管道第三方破坏失效概率计算[J]. 油气储运, 2014, 33 (5)：510-514.

JIN Shubin, ZHENG Honglong，HOU Lei，et al. Calculation of failure probability of the third-party interference for high pressure gas pipeline[J]. Gas storage and transportation, 2014, 33 (5)：510-514.

[3]王禹川, 赵常俊, 黄月等. 含裂纹缺陷油气管道失效概率定量评估[J]. 安全与环境工程，2014，21(3)：126-129.

WANG Yuchuan, ZHAO Changjun, HUANG Yue，et al. Quantitative evaluation of the failure probability of oil and gas pipelines containing crack defects[J]. Safety and environmental engineering，2014，21(3)：126-129.

[4]陈学锋, 于倩秀. 油气长输管道安全评价方法——肯特法简介[J]. 安全、健康和环境，2006，6(3)：27-29.

CHEN Xuefeng, YU Qianxiu. Safety assessment method of oil/gas long pipeline—Kent method's introduction[J]. Safety health & environment，2006，6(3)：27-29.

[5]马晓骊. 故障树分析法在中缅长输原油管道失效风险评价的应用[J]. 新疆石油天然气，2014，10(3)：119-125.

MA Xiaoli. The application of China-BURMA long distance oil pipeline failure risk assessment in the fault tree analysis[J]. Xinjiang oil & gas，2014，10(3)：119-125.

[6]彭星煜, 刘力升, 吕娜，等. 基于BP神经网络的油气长输管道失效概率预测[J]. 全面腐蚀控制，2009，23(5)：12-16.

PENG Xingyu, LIU Lisheng, LYU Na，et al. Long-distance oil/gas pipeline failure rate prediction using BP artificial neural network model[J]. Total corrosion control，2009，23(5)：12-16.

[7]俞树荣, 马欣, 梁端,等. 基于层次分析法的管道风险因素权数确定[J]. 天然气工业，2005，25(6)：132-135.

YU Shurong, MA Xin, LIANG Duan，et al. Weights calculation of pipeline risk factors based on hierarchy analysis method[J]. Natural gas industry，2005，25(6)：132-135.

[8]王瀚翎, 付冬梅. 基于区间直觉模糊数的管道失效概率评估[J]. 油气储运, 2014, 33 (12)：1301-1306.

WANG Hanling, FU Dongmei. Assessment of pipeline failure probability based on interval-valued intuitionistic fuzzy number[J]. Gas storage and transportation, 2014, 33 (12)：1301-1306.

[9]American Petroleum Institute. Risk-Based Inspection Base Resource Document[S]. API pub 581(1st ed), 2002.

[10]高建明, 刘骥, 曾明荣，等. 我国生产安全领域个人风险和社会风险标准界定方法研究[J]. 中国安全科学学报, 2007, 17 (10): 91-95.

GAO Jianming, LIU Ji，ZENG Mingrong,et al. Determination of individual risk and social risk standard about work safety[J]. China safety science journal, 2007, 17 (10): 91-95.

[11]廖芹, 郝志峰, 陈志宏. 数据挖掘与数学建模[M]. 北京：国防工业出版社，2010：292.

[12]Muhlbauer W K.管道风险管理手册(第二版)[M].杨嘉瑜,张德彦,李钦华,等,译. 北京:中国石化出版社,2005：36-64.

[13]杜新燕, 秦风, 黄淑菊，等. 氯离子浓度对土壤腐蚀速率的影响[J]. 广东化工, 2010, 38(9): 41-42.

[14]Du Xinyan, Qin Feng, HUANG Shujyu，et al. Influence of cl- concentration in soil on the corrosion rate[J]. Guangdong Chemical Industry, 2010, 38(9): 41-42.

[15]Jo Y D, Ahn B J. Analysis of hazard areas associated with high-pressure natural gas pipelines[J]. Journal of Loss Prevention in the Process Industries, 2002, 15:179-188.

[16]蒋永清, 任喆, 孙超，等. 埋地管道泄漏天然气在分层填筑土壤扩散数值模拟研究[J]. 中国安全生产科学技术, 2016, 12(6): 105-109.

JIANG Yongqing, REN Zhe, SUN Chao，et al. Numerical simulation research on diffusion of natural gas leaking from buried pipeline in layered filling soil[J]. Journal of Safety Science and Technology, 2016, 12(6): 105-109.

[17]唐保金, 田贯三, 张增刚, 等. 埋地燃气管道泄漏扩散模型[J]. 煤气与热力, 2009, 29(5): B01- B05.

TANG Baojin, TIAN Guansan, ZHANG Zenggang，et al. Model for leakage and diffusion of buried gas pipiline[J]. Gas & Heat, 2009, 29(5): B01- B05.

[18]李雪洁, 金齐杰, 夏茂进，等. 埋地管道泄漏模型初探[J]. 广州化工, 2010, 38(9): 41-42.

LI Xuejie, JIN Qijie, XIA Maojin，et al. Simply study on buried pipeline leakage model[J]. Guangzhou Chemical Industry, 2010, 38(9): 41-42.

[19]严彦, 许昌, 刘德有, 等. 测风数据的时间间隔对风速概率分布参数计算的影响[J]. 可再生能源, 2011, 29(6):24-28.

YAN Yan, XU Chang, LIU Deyou，et al. Study on probabilistic distribution parameters of wind speed influenced by different anemometer time intervals[J]. Renewable Energy Resources, 2011, 29(6):24-28.

[20]宾德，赫尔曼. 统计物理学中的蒙特卡罗模拟方法[M]. 秦克诚，译. 北京: 北京大学出版社, 1994: 165-178.

[21]国家质量监督检验检疫总局. 埋地钢质管道腐蚀防护工程检验: GB/T 19285-2014[S].北京：中国标准出版社, 2014：4.

[22]国家质量监督检验检疫总局. 天然气: GB 17820-2012 [S].北京：中国标准出版社, 2012：1.